24.3圆周角同步练习(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
24.3圆周角
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,为半圆直径,、为圆周上两点,且,与交于点,则图中与相等的角有( )
A.个 B.个 C.个 D.个
2.下列说法:①相等的弦所对的圆心角相等;②等圆中相等的圆心角所对的弧相等;③同圆中等弧所对的圆心角相等.其中正确的是( )
A.①② B.①③ C.②③ D.③
3.如图,在⊙O中,若C是的中点,则图中与∠BAC相等的角有( )
A.1个 B.2个 C.3个 D.4个
4.下列说法正确的是( )
A.顶点在圆上的角叫圆周角
B.三点确定一个圆
C.等弧所对的圆心角相等
D.平分弦的直径垂直于弦,并且平分弦所对的两条弧
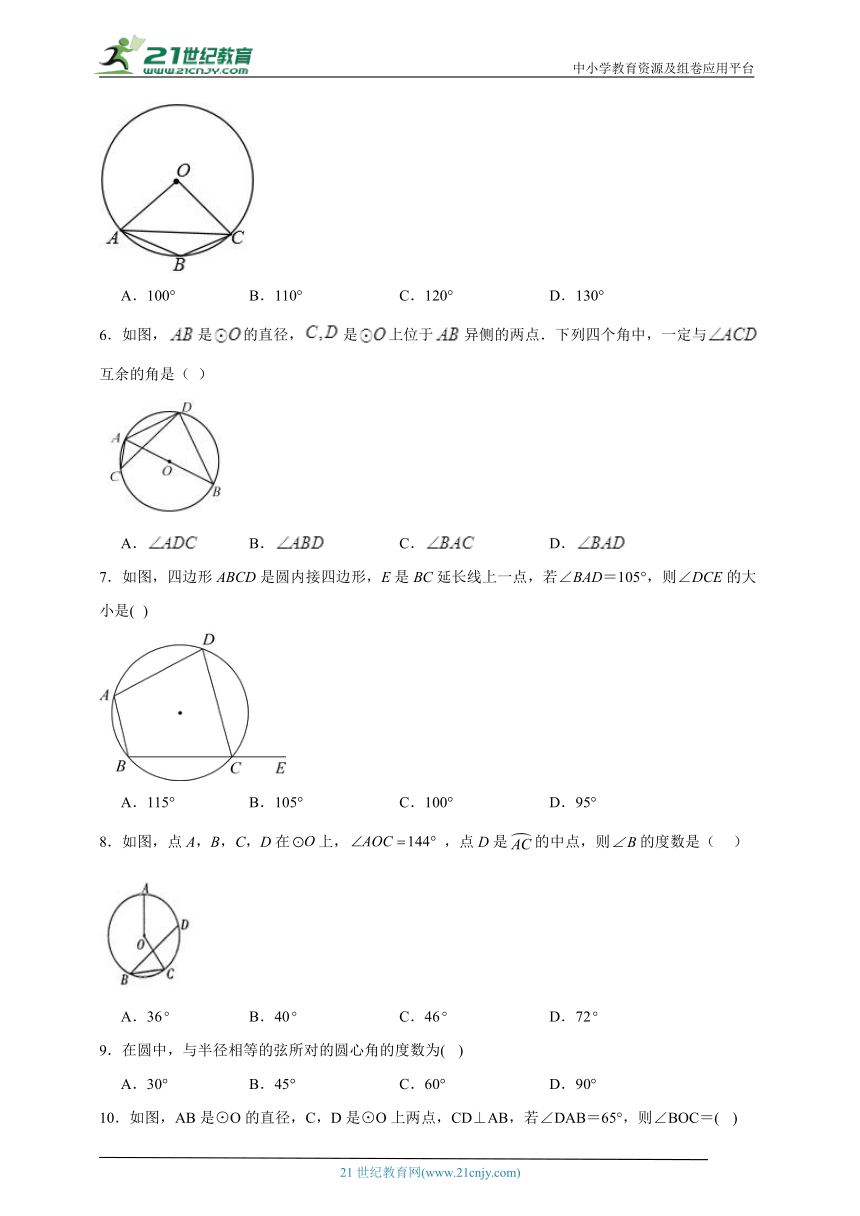
5.如图,点A,B,C均在⊙上,当时,的度数是( )
A.100° B.110° C.120° D.130°
6.如图,是的直径,是上位于异侧的两点.下列四个角中,一定与互余的角是( )
A. B. C. D.
7.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是( )
A.115° B.105° C.100° D.95°
8.如图,点A,B,C,D在上,,点D是的中点,则的度数是( )
A.36 B.40 C.46 D.72
9.在圆中,与半径相等的弦所对的圆心角的度数为( )
A.30° B.45° C.60° D.90°
10.如图,AB是⊙O的直径,C,D是⊙O上两点,CD⊥AB,若∠DAB=65°,则∠BOC=( )
A.25° B.50° C.130° D.155°
11.如图,是的直径,点C、D都在上,若点A是的中点,,,则的长为( )
A. B.6 C. D.8
12.如图, AB为⊙O的直径,弦CD⊥AB于点E,连接AC,OC,OD,若∠A=20°,则∠COD的度数为( )
A.40° B.60° C.80° D.100°
二、填空题
13.如图,已知是半圆上的三等分点,连接和相交于点,有下列结论:①;②;③;④四边形是菱形.其中正确的有 (填序号).
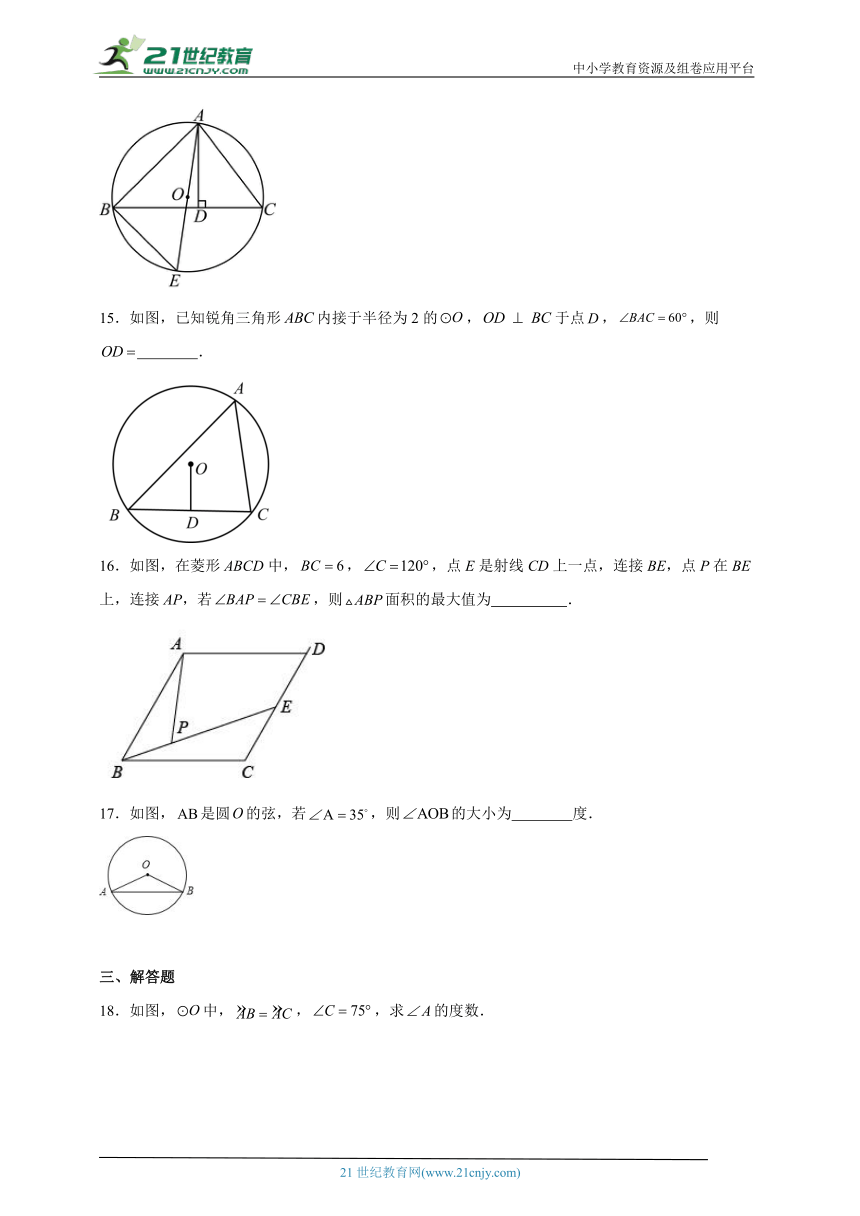
14.如图,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,且AB=,AC=5,AD=4,则⊙O的直径AE= .
15.如图,已知锐角三角形内接于半径为2的,于点,,则 .
16.如图,在菱形ABCD中,,,点E是射线CD上一点,连接BE,点P在BE上,连接AP,若,则面积的最大值为 .
17.如图,是圆的弦,若,则的大小为 度.
三、解答题
18.如图,中,,,求的度数.
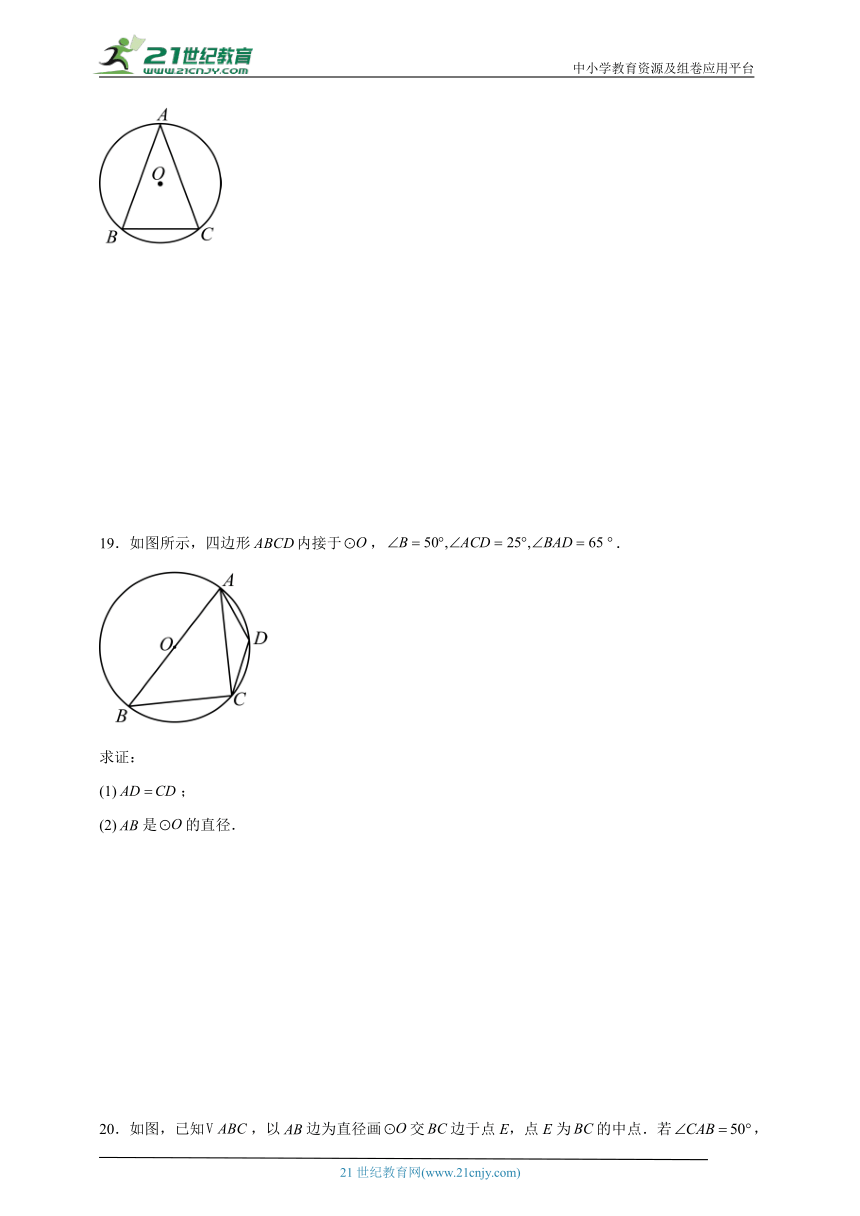
19.如图所示,四边形内接于,.
求证:
(1);
(2)是的直径.
20.如图,已知,以边为直径画交边于点E,点E为的中点.若,求的度数.
21.已知P是上一点,过点P不过圆心的弦,在劣弧和优弧上分别有动点A、B(不与P、Q重合),连接、,若.
(1)如图1,当,,时,求的半径;
(2)如图2,连接,交于点M,点N在线段上(不与P、M重合),连接、,若,探究直线与的位置关系,并证明.
22.如图所示,△ABC内接于⊙O,AD是△ABC的边BC上的高,AE是⊙O的直径,连接BE. 求证:△ABE∽△ADC .
23.如图,是的两条弦.
(1)如果,那么__________,___________.
(2)如果,那么__________,___________.
(3)如果,那么__________,___________.
(4)如果,垂足分别为与相等吗?为什么?
24.为什么有些电影院的座位排列(横排)呈圆弧形?说一说这种设计的合理性.
《24.3圆周角》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C C C D D B A C C
题号 11 12
答案 D C
1.D
【分析】首先与∠BCE相等的角有对顶角∠DCA.由于AB是圆 O的直径,可得∠ADB=90°;已知AD=DE,根据垂径定理可知OD⊥AE;根据等角余角相等,可得出∠DCA=∠ADO=∠DAO;易证得△OAD≌△OED,因此∠DAB=∠ADO=∠ODE=∠DEO;因此与∠BCE相等的角有5个:∠DCA、∠OAD、∠ODA、∠ODE、∠OED.
【详解】解:∵在△ADO和△DOE中
∴△OAD≌△ODE(SSS),
∴∠DAB=∠EDO,∠ADO=∠DEO,
∵AO=DO,
∴∠DAB=∠ADO,
∴∠DAB=∠ADO=∠ODE=∠DEO;
∵AB是直径,
∴
∵AD=DE,
∴∠ABD=∠DBE,
∴
∴∠DAB=∠BCE,
∵∠DCA=∠BCE(对顶角相等)
∴∠DCA=∠DAB=∠ADO=∠ODE=∠DEO,
则与∠ECB相等的角有5个.
故选D.
【点睛】考查全等三角形的判定与性质,圆周角定理,掌握全等三角形的判定与性质是解题的关键.
2.C
【分析】根据圆心角、弧、弦的关系进行判断即可.
【详解】①∵在同圆或等圆中,相等的弦所对的圆心角相等,故不正确;②等圆中相等的圆心角所对的弧相等,正确;③同圆中等弧所对的圆心角相等,正确.
故选C.
【点睛】本题考查了圆心角、弧、弦之间的关系,在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对的其余各组量都分别相等.
3.C
【详解】解:∵点C是弧BD的中点,
∴,
∴∠BAC=∠CAD,
∠BAC=∠BDC,
∠CAD=∠CBD,
∴∠CAD=∠BDC=∠CBD=∠BAC,
于是图中与∠BAC相等的角共有3个,
故选C.
【点睛】本题考查圆周角定理;圆心角、弧、弦的关系.
4.C
【分析】本题主要考查了垂径定理、确定圆的条件、圆周角定理等圆的有关性质及定理,利用圆的有关性质及定理,分别判断后即可确定正确的选项.
【详解】解:A、顶点在圆上且两边都与圆相交的角叫圆周角,故该选项错误;
B、不在同一条直线上的三点确定一个圆,故该选项错误;
C、同弧或等弧所对的圆心角相等,故该选项正确;
D、平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧,故该选项错误;
故选C.
5.D
【分析】在优弧AB上任意找一点D,根据三角形的内角和得到∠AOC=100°,根据圆周角定理得到∠D=∠AOC=50°,即可根据圆内接四边形的对角互补得到结论.
【详解】
解:在优弧AB上任意找一点D,连接AD,CD,
∵OA=OC,∠OAC=40°,
∴∠OAC=∠OCA=40°,
∴∠AOC=180°-40°-40°=100°,
∴∠D=∠AOC=50°,
∵四边形ABCD内接于⊙O,
∴∠D+∠B=180°,
∴∠B=180°-50°=130°,
故选:D.
【点睛】本题考查了圆周角定理,圆内接四边形的性质,正确的作出辅助线是解题的关键.
6.D
【详解】∵AB是直径,∴∠ADB=90°,∴∠BAD+∠B=90°,∵∠ACD=∠B,∴∠BAD+∠ACD=90°,故选D.
7.B
【分析】根据圆内接四边形的对角互补得到∠BAD+∠BCD=180°,而∠BCD与∠DEC为邻补角,得到∠DCE=∠BAD=105°.
【详解】解:∵四边形ABCD是圆内接四边形,
∴∠BAD+∠BCD=180°,
而∠BCD+∠DCE=180°,
∴∠DCE=∠BAD,
而∠BAD=105°,
∴∠DCE=105°.
故选:B.
8.A
【分析】连接OD,根据点D是中点求出∠COD,再利用圆周角定理得出结果.
【详解】解:连接OD,
∵D是的中点,
∴∠COD= ,
∴∠B= ,
故选择A.
【点睛】本题考查圆周角定理以及弧和圆心角关系,注意通过弧进行角的转化是解决问题的关键.
9.C
【分析】画出符合题意的几何图形,证明△OAB是等边三角形即可得到此弦所对圆心角的度数.
【详解】解:如图,
∵OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°.
故选:C.
【点睛】本题考查了圆心角、弧、弦的关系.解答该题时,利用了等边三角形的判定和性质,熟记和圆有关的各种性质是解题的关键.
10.C
【详解】解:∵CD⊥AB.∠DAB=65°,
∴∠ADC=90°﹣∠DAB=25°,
∴∠AOC=2∠ADC=50°,
∴∠BOC=180°﹣∠AOC=130°.
故选C.
考点:圆周角定理;
11.D
【分析】本题考查了垂径定理、解直角三角形,正确作出辅助线是解题的关键.
连接、,根据垂径定理得,可得出,再根据同弧所对的圆心角是圆周角的两倍得出,易得出,然后根据正弦的定义即可得出,最后根据直径是半径的2倍,即可得出答案.
【详解】解:连接、,
点A是的中点,
,设垂足为点,
,
,
和所对的弧都是,
,
,且,
,
,
,
在中,,,,,
,
是的直径,
,
故选D.
12.C
【分析】利用圆周角与圆心角的关系得出∠COB=40°,再根据垂径定理进一步可得出∠DOB=∠COB,最后即可得出答案.
【详解】∵∠A=20°,
∴∠COB=2∠A=40°,
∵CD⊥AB,OC=OD,
∴∠DOB=∠COB=40°,
∴∠COD=∠DOB+∠COB=80°.
故选:C.
【点睛】本题主要考查了圆周角、圆心角与垂径定理的综合运用,熟练掌握相关概念是解题关键.
13.①②③④
【分析】①首先根据点C,D是半圆上的三等分,求出的度数;然后根据圆周角定理,求出的度数即可;②根据三角形的内角和定理,求出,即可判断出;③根据垂径定理判断出E是的中点,然后得到是的中位线,即可判断出,④先证明,再证明是等边三角形,得到,根据菱形的判定方法可判断四边形是菱形.
【详解】解:连接,
∵已知是半圆上的三等分点,
∴,
∴,故①正确;
∴,
∴,故②正确;
∴,,
∴是的中位线,
∴,故③正确;
∵是半圆O的直径,
∴,又,
∴,
∵,,
∴是等边三角形,
∴,
∴四边形是平行四边形,又,
∴四边形是菱形.故④正确,
故答案为:①②③④.
【点睛】本题主要考查了圆周角定理,垂径定理,圆心角、弧、弦三者的关系,菱形的判定和性质,等边三角形的判定,三角形的内角和定义及中位线性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
14..
【详解】由圆周角定理可知,∠E=∠C,
∵∠ABE=∠ADC=90°,∠E=∠C,
∴△ABE∽△ACD.
∴AB:AD=AE:AC,
∵AB=4,AC=5,AD=4,
∴4:4=AE:5,
∴AE=5,
故答案为5.
【点睛】本题考查了圆周角定理、相似三角形的性质和判定的应用,解此题的关键是证出△ABE∽△ACD.
15.1
【分析】连接OB和OC,根据圆周角定理得出∠BOC的度数,再依据等腰三角形的性质得到∠BOD的度数,结合直角三角形的性质可得OD.
【详解】解:连接OB和OC,
∵△ABC内接于半径为2的圆O,∠BAC=60°,
∴∠BOC=120°,OB=OC=2,
∵OD⊥BC,OB=OC,
∴∠BOD=∠COD=60°,
∴∠OBD=30°,
∴OD=OB=1,
故答案为:1.
【点睛】本题考查了圆周角定理,三角形外接圆的性质,等腰三角形三线合一,30°的直角三角形的性质,解题时需要添加辅助线,从而运用圆周角定理.
16.
【分析】若要使的面积最大,底AB固定,故只要AB边上的高最大时,即三角形面积最大;可证,故可知点P在△APB的外接圆的劣弧上,当点P在劣弧的中点处,△APB的面积最大,求出AB边上的高即可求解.
【详解】解:∵四边形ABCD是菱形,
∴AB=BC=6,AB//CD,
∴
∵,
∴ 即,
∵,
∴,
∵,
∴点P在△APB的外接圆上,
若要使的面积最大,底AB固定,,故只要AB边上的高最大时,即三角形面积最大;此时点P在劣弧的中点处,如图,
设点O为△APB的外接圆的圆心,OP⊥AB于点F,
∴,,
∴
∴
由勾股定理得,
∴
∴PF=
∴
即面积的最大值为.
故答案为:.
【点睛】本题考查了菱形的性质,三角形的面积公式,解直角三角形,垂径定理等知识,正确作出辅助圆,熟练掌握知识点是解题的关键.
17.110
【分析】由半径相等可求得∠A=∠B,在△OAB中利用三角形内角和定理可求得答案.
【详解】解:∵AB是O的弦,
∴OA=OB,
∴
∴
故答案为110.
【点睛】考查圆的有关性质,掌握同圆中的半径相等是解题的关键.
18.
【分析】根据同圆或等圆中等弧所对圆周角相等,得出,再利用三角形内角和定理求出即可.
此题主要考查圆周角的性质,三角形内角和定理,解题的关键是熟知同圆或等圆中等弧所对圆周角相等.
【详解】∵,
,
.
19.(1)见解析
(2)见解析
【分析】(1)连接,根据圆周角定理得,再由可计算出,则,然后根据圆心角、弧、弦的关系即可得到;
(2)根据三角形内角和定理可计算出,则根据圆周角的推理即可得到为的直径.
【详解】(1)证明:连接,如图,
,
而,
,
,
,
;
(2),,
,
为的直径.
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,的圆周角所对的弦是直径.
20.
【分析】本题主要考查了圆周角定理,等腰三角形的性质,线段垂直平分线的性质.连结,可得,从而得到,即可求解.
【详解】解:如图,连结,
∵边为的直径,
∴.
,
∵点E是的中点,
∴.
∴,
,
∴.
21.(1);
(2)平行,证明见解析.
【分析】(1)连接,首先根据已知条件求出,进而判断出为直径,然后再根据勾股定理求出的长度,即可求出的半径;
(2)连接、、,延长交于点,根据圆周角定理可得,再结合已知条件可得,根据已知条件可得,进而求得,再根据三线合一得到,最后根据平行线的判定定理证出结论.
【详解】(1)解:如图所示,连接,
∵ ,,
∴,
∴为直径,
∵,,
∴在中根据勾股定理得:
,
∴或(舍去),
∴半径为.
(2)解:直线与的位置关系为:,
证明:连接、、,交于点F,延长交于点E,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
又∵,
∴,(三线合一),
∴,
∴.
【点睛】本题考查了勾股定理、圆周角定理、等弧所对的圆心角相等、相等的圆周角所对的弧相等、三线合一、平行线的判定定理,是一道综合题,正确作出辅助线并灵活运用相关知识是解题的关键.
22.见解析
【分析】由AE是⊙O的直径可得∠ABE是直角,所以∠ABE=∠ADC,由∠C、∠E是同弧 所对的圆周角可得∠C=∠E,所以△ABE与△ADC相似.
【详解】证明:∵AE是⊙O的直径,
∴∠ABE=90°,
∵AD是△ABC的边BC上的高,
∴∠ADC=90°,
∴∠ABE=∠ADC.
又∵同弧所对的圆周角相等,
∴∠BEA=∠DCA.
∴△ABE ∽△ADC.
【点睛】考查了圆周角的性质和三角形相似的判定方法,解题关键是由利用了圆周角性质得出∠BEA=∠DCA.
23.(1),∠AOB=∠COD;(2)AB=CD;∠AOB=∠COD;(3)AB=CD,;(4)OE与OF相等;见解析
【分析】(1)、(2)、(3)利用圆心角、弧、弦的关系直接求解;
(4)先利用垂径定理得到AE=BE,CF=DF,而AB=CD,则AE=CF,然后利用勾股定理可判断OE=OF.
【详解】(1)如果AB=CD,那么,∠AOB=∠COD;
(2)如果,那么∠AOB=∠COD;AB=CD;
(3)如果∠AOB=∠COD,那么,AB=CD;
(4)OE与OF相等.理由如下:
∵OE⊥AB于点E,OF⊥CD于点F,
∴AE=BE,CF=DF,
而AB=CD,
∴AE=CF,
∵OE=
OF=,OA=OC,
∴OE=OF.
故答案为:(1),∠AOB=∠COD;(2)AB=CD;∠AOB=∠COD;(3)AB=CD,.
【点睛】本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了垂径定理.
24.见解析
【分析】根据题意画出示意图,其中BC表示电影幕的宽,G、I分别为圆弧形排列的座位中的任意两个,根据图形可知∠BGC、∠BJC分别为两个座位的视角,由此结合圆周角定理的推论求解即可.
【详解】根据题意画出图形,BC表示电影幕的宽,
由同弧所对圆周角相等可知∠BGC=∠BJC,即同排的观众视角相等.
【点睛】本题是圆周角定理的推论在实际问题中的应用,解题的关键是要理解在同排的观众视角需相同.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.3圆周角
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,为半圆直径,、为圆周上两点,且,与交于点,则图中与相等的角有( )
A.个 B.个 C.个 D.个
2.下列说法:①相等的弦所对的圆心角相等;②等圆中相等的圆心角所对的弧相等;③同圆中等弧所对的圆心角相等.其中正确的是( )
A.①② B.①③ C.②③ D.③
3.如图,在⊙O中,若C是的中点,则图中与∠BAC相等的角有( )
A.1个 B.2个 C.3个 D.4个
4.下列说法正确的是( )
A.顶点在圆上的角叫圆周角
B.三点确定一个圆
C.等弧所对的圆心角相等
D.平分弦的直径垂直于弦,并且平分弦所对的两条弧
5.如图,点A,B,C均在⊙上,当时,的度数是( )
A.100° B.110° C.120° D.130°
6.如图,是的直径,是上位于异侧的两点.下列四个角中,一定与互余的角是( )
A. B. C. D.
7.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是( )
A.115° B.105° C.100° D.95°
8.如图,点A,B,C,D在上,,点D是的中点,则的度数是( )
A.36 B.40 C.46 D.72
9.在圆中,与半径相等的弦所对的圆心角的度数为( )
A.30° B.45° C.60° D.90°
10.如图,AB是⊙O的直径,C,D是⊙O上两点,CD⊥AB,若∠DAB=65°,则∠BOC=( )
A.25° B.50° C.130° D.155°
11.如图,是的直径,点C、D都在上,若点A是的中点,,,则的长为( )
A. B.6 C. D.8
12.如图, AB为⊙O的直径,弦CD⊥AB于点E,连接AC,OC,OD,若∠A=20°,则∠COD的度数为( )
A.40° B.60° C.80° D.100°
二、填空题
13.如图,已知是半圆上的三等分点,连接和相交于点,有下列结论:①;②;③;④四边形是菱形.其中正确的有 (填序号).
14.如图,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,且AB=,AC=5,AD=4,则⊙O的直径AE= .
15.如图,已知锐角三角形内接于半径为2的,于点,,则 .
16.如图,在菱形ABCD中,,,点E是射线CD上一点,连接BE,点P在BE上,连接AP,若,则面积的最大值为 .
17.如图,是圆的弦,若,则的大小为 度.
三、解答题
18.如图,中,,,求的度数.
19.如图所示,四边形内接于,.
求证:
(1);
(2)是的直径.
20.如图,已知,以边为直径画交边于点E,点E为的中点.若,求的度数.
21.已知P是上一点,过点P不过圆心的弦,在劣弧和优弧上分别有动点A、B(不与P、Q重合),连接、,若.
(1)如图1,当,,时,求的半径;
(2)如图2,连接,交于点M,点N在线段上(不与P、M重合),连接、,若,探究直线与的位置关系,并证明.
22.如图所示,△ABC内接于⊙O,AD是△ABC的边BC上的高,AE是⊙O的直径,连接BE. 求证:△ABE∽△ADC .
23.如图,是的两条弦.
(1)如果,那么__________,___________.
(2)如果,那么__________,___________.
(3)如果,那么__________,___________.
(4)如果,垂足分别为与相等吗?为什么?
24.为什么有些电影院的座位排列(横排)呈圆弧形?说一说这种设计的合理性.
《24.3圆周角》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C C C D D B A C C
题号 11 12
答案 D C
1.D
【分析】首先与∠BCE相等的角有对顶角∠DCA.由于AB是圆 O的直径,可得∠ADB=90°;已知AD=DE,根据垂径定理可知OD⊥AE;根据等角余角相等,可得出∠DCA=∠ADO=∠DAO;易证得△OAD≌△OED,因此∠DAB=∠ADO=∠ODE=∠DEO;因此与∠BCE相等的角有5个:∠DCA、∠OAD、∠ODA、∠ODE、∠OED.
【详解】解:∵在△ADO和△DOE中
∴△OAD≌△ODE(SSS),
∴∠DAB=∠EDO,∠ADO=∠DEO,
∵AO=DO,
∴∠DAB=∠ADO,
∴∠DAB=∠ADO=∠ODE=∠DEO;
∵AB是直径,
∴
∵AD=DE,
∴∠ABD=∠DBE,
∴
∴∠DAB=∠BCE,
∵∠DCA=∠BCE(对顶角相等)
∴∠DCA=∠DAB=∠ADO=∠ODE=∠DEO,
则与∠ECB相等的角有5个.
故选D.
【点睛】考查全等三角形的判定与性质,圆周角定理,掌握全等三角形的判定与性质是解题的关键.
2.C
【分析】根据圆心角、弧、弦的关系进行判断即可.
【详解】①∵在同圆或等圆中,相等的弦所对的圆心角相等,故不正确;②等圆中相等的圆心角所对的弧相等,正确;③同圆中等弧所对的圆心角相等,正确.
故选C.
【点睛】本题考查了圆心角、弧、弦之间的关系,在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对的其余各组量都分别相等.
3.C
【详解】解:∵点C是弧BD的中点,
∴,
∴∠BAC=∠CAD,
∠BAC=∠BDC,
∠CAD=∠CBD,
∴∠CAD=∠BDC=∠CBD=∠BAC,
于是图中与∠BAC相等的角共有3个,
故选C.
【点睛】本题考查圆周角定理;圆心角、弧、弦的关系.
4.C
【分析】本题主要考查了垂径定理、确定圆的条件、圆周角定理等圆的有关性质及定理,利用圆的有关性质及定理,分别判断后即可确定正确的选项.
【详解】解:A、顶点在圆上且两边都与圆相交的角叫圆周角,故该选项错误;
B、不在同一条直线上的三点确定一个圆,故该选项错误;
C、同弧或等弧所对的圆心角相等,故该选项正确;
D、平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧,故该选项错误;
故选C.
5.D
【分析】在优弧AB上任意找一点D,根据三角形的内角和得到∠AOC=100°,根据圆周角定理得到∠D=∠AOC=50°,即可根据圆内接四边形的对角互补得到结论.
【详解】
解:在优弧AB上任意找一点D,连接AD,CD,
∵OA=OC,∠OAC=40°,
∴∠OAC=∠OCA=40°,
∴∠AOC=180°-40°-40°=100°,
∴∠D=∠AOC=50°,
∵四边形ABCD内接于⊙O,
∴∠D+∠B=180°,
∴∠B=180°-50°=130°,
故选:D.
【点睛】本题考查了圆周角定理,圆内接四边形的性质,正确的作出辅助线是解题的关键.
6.D
【详解】∵AB是直径,∴∠ADB=90°,∴∠BAD+∠B=90°,∵∠ACD=∠B,∴∠BAD+∠ACD=90°,故选D.
7.B
【分析】根据圆内接四边形的对角互补得到∠BAD+∠BCD=180°,而∠BCD与∠DEC为邻补角,得到∠DCE=∠BAD=105°.
【详解】解:∵四边形ABCD是圆内接四边形,
∴∠BAD+∠BCD=180°,
而∠BCD+∠DCE=180°,
∴∠DCE=∠BAD,
而∠BAD=105°,
∴∠DCE=105°.
故选:B.
8.A
【分析】连接OD,根据点D是中点求出∠COD,再利用圆周角定理得出结果.
【详解】解:连接OD,
∵D是的中点,
∴∠COD= ,
∴∠B= ,
故选择A.
【点睛】本题考查圆周角定理以及弧和圆心角关系,注意通过弧进行角的转化是解决问题的关键.
9.C
【分析】画出符合题意的几何图形,证明△OAB是等边三角形即可得到此弦所对圆心角的度数.
【详解】解:如图,
∵OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°.
故选:C.
【点睛】本题考查了圆心角、弧、弦的关系.解答该题时,利用了等边三角形的判定和性质,熟记和圆有关的各种性质是解题的关键.
10.C
【详解】解:∵CD⊥AB.∠DAB=65°,
∴∠ADC=90°﹣∠DAB=25°,
∴∠AOC=2∠ADC=50°,
∴∠BOC=180°﹣∠AOC=130°.
故选C.
考点:圆周角定理;
11.D
【分析】本题考查了垂径定理、解直角三角形,正确作出辅助线是解题的关键.
连接、,根据垂径定理得,可得出,再根据同弧所对的圆心角是圆周角的两倍得出,易得出,然后根据正弦的定义即可得出,最后根据直径是半径的2倍,即可得出答案.
【详解】解:连接、,
点A是的中点,
,设垂足为点,
,
,
和所对的弧都是,
,
,且,
,
,
,
在中,,,,,
,
是的直径,
,
故选D.
12.C
【分析】利用圆周角与圆心角的关系得出∠COB=40°,再根据垂径定理进一步可得出∠DOB=∠COB,最后即可得出答案.
【详解】∵∠A=20°,
∴∠COB=2∠A=40°,
∵CD⊥AB,OC=OD,
∴∠DOB=∠COB=40°,
∴∠COD=∠DOB+∠COB=80°.
故选:C.
【点睛】本题主要考查了圆周角、圆心角与垂径定理的综合运用,熟练掌握相关概念是解题关键.
13.①②③④
【分析】①首先根据点C,D是半圆上的三等分,求出的度数;然后根据圆周角定理,求出的度数即可;②根据三角形的内角和定理,求出,即可判断出;③根据垂径定理判断出E是的中点,然后得到是的中位线,即可判断出,④先证明,再证明是等边三角形,得到,根据菱形的判定方法可判断四边形是菱形.
【详解】解:连接,
∵已知是半圆上的三等分点,
∴,
∴,故①正确;
∴,
∴,故②正确;
∴,,
∴是的中位线,
∴,故③正确;
∵是半圆O的直径,
∴,又,
∴,
∵,,
∴是等边三角形,
∴,
∴四边形是平行四边形,又,
∴四边形是菱形.故④正确,
故答案为:①②③④.
【点睛】本题主要考查了圆周角定理,垂径定理,圆心角、弧、弦三者的关系,菱形的判定和性质,等边三角形的判定,三角形的内角和定义及中位线性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
14..
【详解】由圆周角定理可知,∠E=∠C,
∵∠ABE=∠ADC=90°,∠E=∠C,
∴△ABE∽△ACD.
∴AB:AD=AE:AC,
∵AB=4,AC=5,AD=4,
∴4:4=AE:5,
∴AE=5,
故答案为5.
【点睛】本题考查了圆周角定理、相似三角形的性质和判定的应用,解此题的关键是证出△ABE∽△ACD.
15.1
【分析】连接OB和OC,根据圆周角定理得出∠BOC的度数,再依据等腰三角形的性质得到∠BOD的度数,结合直角三角形的性质可得OD.
【详解】解:连接OB和OC,
∵△ABC内接于半径为2的圆O,∠BAC=60°,
∴∠BOC=120°,OB=OC=2,
∵OD⊥BC,OB=OC,
∴∠BOD=∠COD=60°,
∴∠OBD=30°,
∴OD=OB=1,
故答案为:1.
【点睛】本题考查了圆周角定理,三角形外接圆的性质,等腰三角形三线合一,30°的直角三角形的性质,解题时需要添加辅助线,从而运用圆周角定理.
16.
【分析】若要使的面积最大,底AB固定,故只要AB边上的高最大时,即三角形面积最大;可证,故可知点P在△APB的外接圆的劣弧上,当点P在劣弧的中点处,△APB的面积最大,求出AB边上的高即可求解.
【详解】解:∵四边形ABCD是菱形,
∴AB=BC=6,AB//CD,
∴
∵,
∴ 即,
∵,
∴,
∵,
∴点P在△APB的外接圆上,
若要使的面积最大,底AB固定,,故只要AB边上的高最大时,即三角形面积最大;此时点P在劣弧的中点处,如图,
设点O为△APB的外接圆的圆心,OP⊥AB于点F,
∴,,
∴
∴
由勾股定理得,
∴
∴PF=
∴
即面积的最大值为.
故答案为:.
【点睛】本题考查了菱形的性质,三角形的面积公式,解直角三角形,垂径定理等知识,正确作出辅助圆,熟练掌握知识点是解题的关键.
17.110
【分析】由半径相等可求得∠A=∠B,在△OAB中利用三角形内角和定理可求得答案.
【详解】解:∵AB是O的弦,
∴OA=OB,
∴
∴
故答案为110.
【点睛】考查圆的有关性质,掌握同圆中的半径相等是解题的关键.
18.
【分析】根据同圆或等圆中等弧所对圆周角相等,得出,再利用三角形内角和定理求出即可.
此题主要考查圆周角的性质,三角形内角和定理,解题的关键是熟知同圆或等圆中等弧所对圆周角相等.
【详解】∵,
,
.
19.(1)见解析
(2)见解析
【分析】(1)连接,根据圆周角定理得,再由可计算出,则,然后根据圆心角、弧、弦的关系即可得到;
(2)根据三角形内角和定理可计算出,则根据圆周角的推理即可得到为的直径.
【详解】(1)证明:连接,如图,
,
而,
,
,
,
;
(2),,
,
为的直径.
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,的圆周角所对的弦是直径.
20.
【分析】本题主要考查了圆周角定理,等腰三角形的性质,线段垂直平分线的性质.连结,可得,从而得到,即可求解.
【详解】解:如图,连结,
∵边为的直径,
∴.
,
∵点E是的中点,
∴.
∴,
,
∴.
21.(1);
(2)平行,证明见解析.
【分析】(1)连接,首先根据已知条件求出,进而判断出为直径,然后再根据勾股定理求出的长度,即可求出的半径;
(2)连接、、,延长交于点,根据圆周角定理可得,再结合已知条件可得,根据已知条件可得,进而求得,再根据三线合一得到,最后根据平行线的判定定理证出结论.
【详解】(1)解:如图所示,连接,
∵ ,,
∴,
∴为直径,
∵,,
∴在中根据勾股定理得:
,
∴或(舍去),
∴半径为.
(2)解:直线与的位置关系为:,
证明:连接、、,交于点F,延长交于点E,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
又∵,
∴,(三线合一),
∴,
∴.
【点睛】本题考查了勾股定理、圆周角定理、等弧所对的圆心角相等、相等的圆周角所对的弧相等、三线合一、平行线的判定定理,是一道综合题,正确作出辅助线并灵活运用相关知识是解题的关键.
22.见解析
【分析】由AE是⊙O的直径可得∠ABE是直角,所以∠ABE=∠ADC,由∠C、∠E是同弧 所对的圆周角可得∠C=∠E,所以△ABE与△ADC相似.
【详解】证明:∵AE是⊙O的直径,
∴∠ABE=90°,
∵AD是△ABC的边BC上的高,
∴∠ADC=90°,
∴∠ABE=∠ADC.
又∵同弧所对的圆周角相等,
∴∠BEA=∠DCA.
∴△ABE ∽△ADC.
【点睛】考查了圆周角的性质和三角形相似的判定方法,解题关键是由利用了圆周角性质得出∠BEA=∠DCA.
23.(1),∠AOB=∠COD;(2)AB=CD;∠AOB=∠COD;(3)AB=CD,;(4)OE与OF相等;见解析
【分析】(1)、(2)、(3)利用圆心角、弧、弦的关系直接求解;
(4)先利用垂径定理得到AE=BE,CF=DF,而AB=CD,则AE=CF,然后利用勾股定理可判断OE=OF.
【详解】(1)如果AB=CD,那么,∠AOB=∠COD;
(2)如果,那么∠AOB=∠COD;AB=CD;
(3)如果∠AOB=∠COD,那么,AB=CD;
(4)OE与OF相等.理由如下:
∵OE⊥AB于点E,OF⊥CD于点F,
∴AE=BE,CF=DF,
而AB=CD,
∴AE=CF,
∵OE=
OF=,OA=OC,
∴OE=OF.
故答案为:(1),∠AOB=∠COD;(2)AB=CD;∠AOB=∠COD;(3)AB=CD,.
【点睛】本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了垂径定理.
24.见解析
【分析】根据题意画出示意图,其中BC表示电影幕的宽,G、I分别为圆弧形排列的座位中的任意两个,根据图形可知∠BGC、∠BJC分别为两个座位的视角,由此结合圆周角定理的推论求解即可.
【详解】根据题意画出图形,BC表示电影幕的宽,
由同弧所对圆周角相等可知∠BGC=∠BJC,即同排的观众视角相等.
【点睛】本题是圆周角定理的推论在实际问题中的应用,解题的关键是要理解在同排的观众视角需相同.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
