第32章 投影与视图 单元练习(含解析)
文档属性
| 名称 | 第32章 投影与视图 单元练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 872.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-02 05:48:44 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第三十二章投影与视图
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知圆锥底面半径为1,母线长为4,地面圆周上有一点A,一只蚂蚁从点A出发沿圆锥侧面运动一周后到达母线PA中点B,则蚂蚁爬行的最短路程为( )
A. B. C. D.
2.下图是直观图的三视图,它对应的直观图是下图中的( )
A.A B.B C.C D.D
3.如图,将一张边长为3的正方形纸片按虚线裁剪后恰好围成一个底面是正三角形的棱柱,则这个棱柱的侧面积为( )
A.9-3 B.9 C.9- D.9-
4.图l、2给出了一个由小立方体组成的几何体的正面看,左面看,其中小正方形中的数字表示该位置上小立方体的个数,则它的上面看不能画成( )
图1 图2
A. B. C. D.
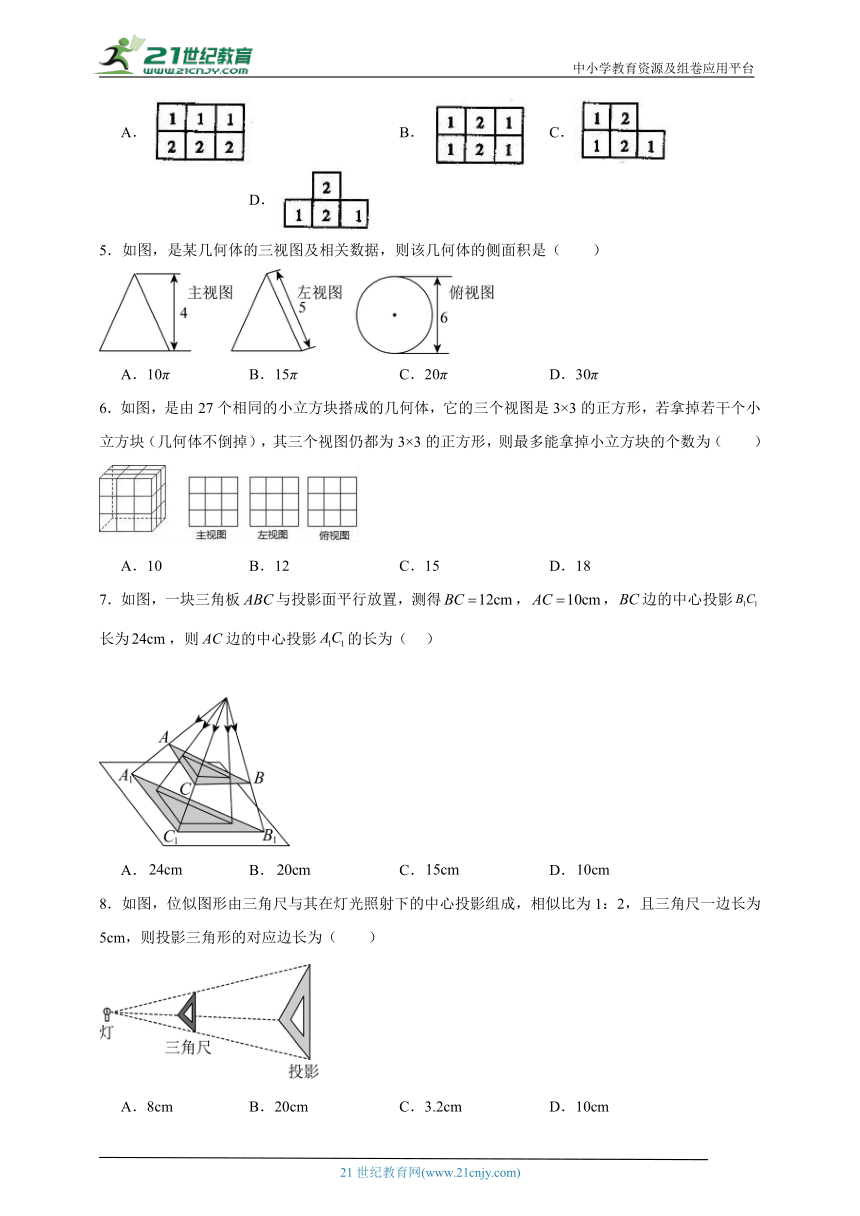
5.如图,是某几何体的三视图及相关数据,则该几何体的侧面积是( )
A.10π B.15π C.20π D.30π
6.如图,是由27个相同的小立方块搭成的几何体,它的三个视图是3×3的正方形,若拿掉若干个小立方块(几何体不倒掉),其三个视图仍都为3×3的正方形,则最多能拿掉小立方块的个数为( )
A.10 B.12 C.15 D.18
7.如图,一块三角板与投影面平行放置,测得,,边的中心投影长为,则边的中心投影的长为( )
A. B. C. D.
8.如图,位似图形由三角尺与其在灯光照射下的中心投影组成,相似比为1:2,且三角尺一边长为5cm,则投影三角形的对应边长为( )
A.8cm B.20cm C.3.2cm D.10cm
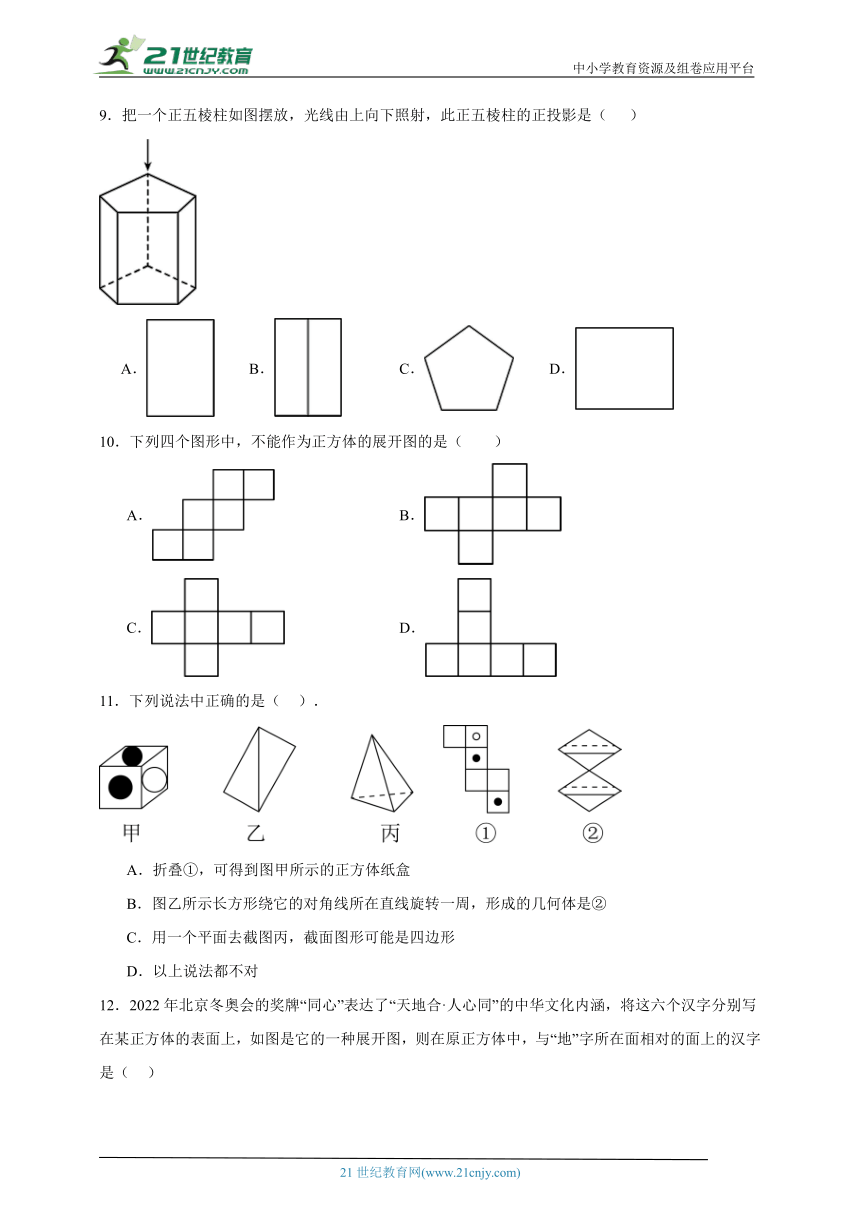
9.把一个正五棱柱如图摆放,光线由上向下照射,此正五棱柱的正投影是( )
A. B. C. D.
10.下列四个图形中,不能作为正方体的展开图的是( )
A. B.
C. D.
11.下列说法中正确的是( ).
A.折叠①,可得到图甲所示的正方体纸盒
B.图乙所示长方形绕它的对角线所在直线旋转一周,形成的几何体是②
C.用一个平面去截图丙,截面图形可能是四边形
D.以上说法都不对
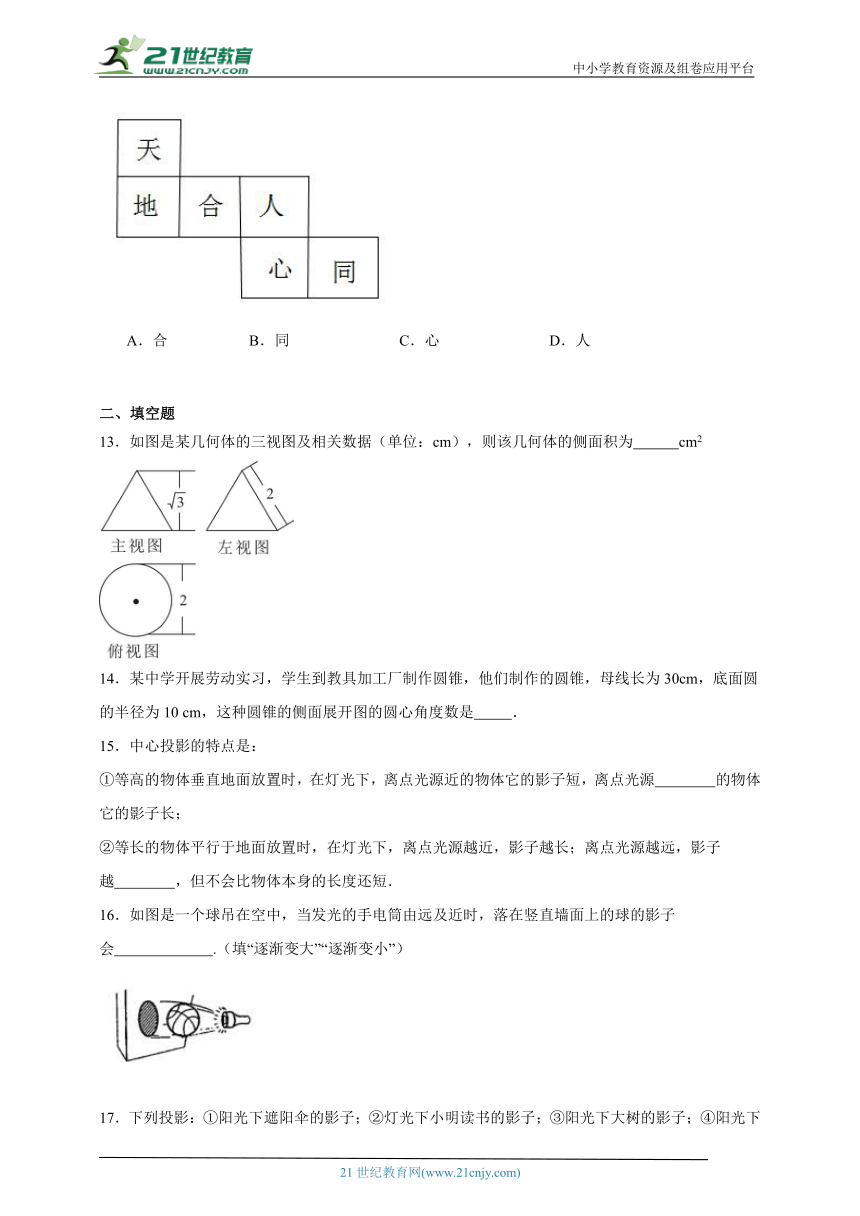
12.2022年北京冬奥会的奖牌“同心”表达了“天地合·人心同”的中华文化内涵,将这六个汉字分别写在某正方体的表面上,如图是它的一种展开图,则在原正方体中,与“地”字所在面相对的面上的汉字是( )
A.合 B.同 C.心 D.人
二、填空题
13.如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为 cm2
14.某中学开展劳动实习,学生到教具加工厂制作圆锥,他们制作的圆锥,母线长为30cm,底面圆的半径为10 cm,这种圆锥的侧面展开图的圆心角度数是 .
15.中心投影的特点是:
①等高的物体垂直地面放置时,在灯光下,离点光源近的物体它的影子短,离点光源 的物体它的影子长;
②等长的物体平行于地面放置时,在灯光下,离点光源越近,影子越长;离点光源越远,影子越 ,但不会比物体本身的长度还短.
16.如图是一个球吊在空中,当发光的手电筒由远及近时,落在竖直墙面上的球的影子会 .(填“逐渐变大”“逐渐变小”)
17.下列投影:①阳光下遮阳伞的影子;②灯光下小明读书的影子;③阳光下大树的影子;④阳光下农民锄地的影子;⑤路灯下木杆的影子.其中属于平行投影的是 ,属于中心投影的是 .(填序号)
三、解答题
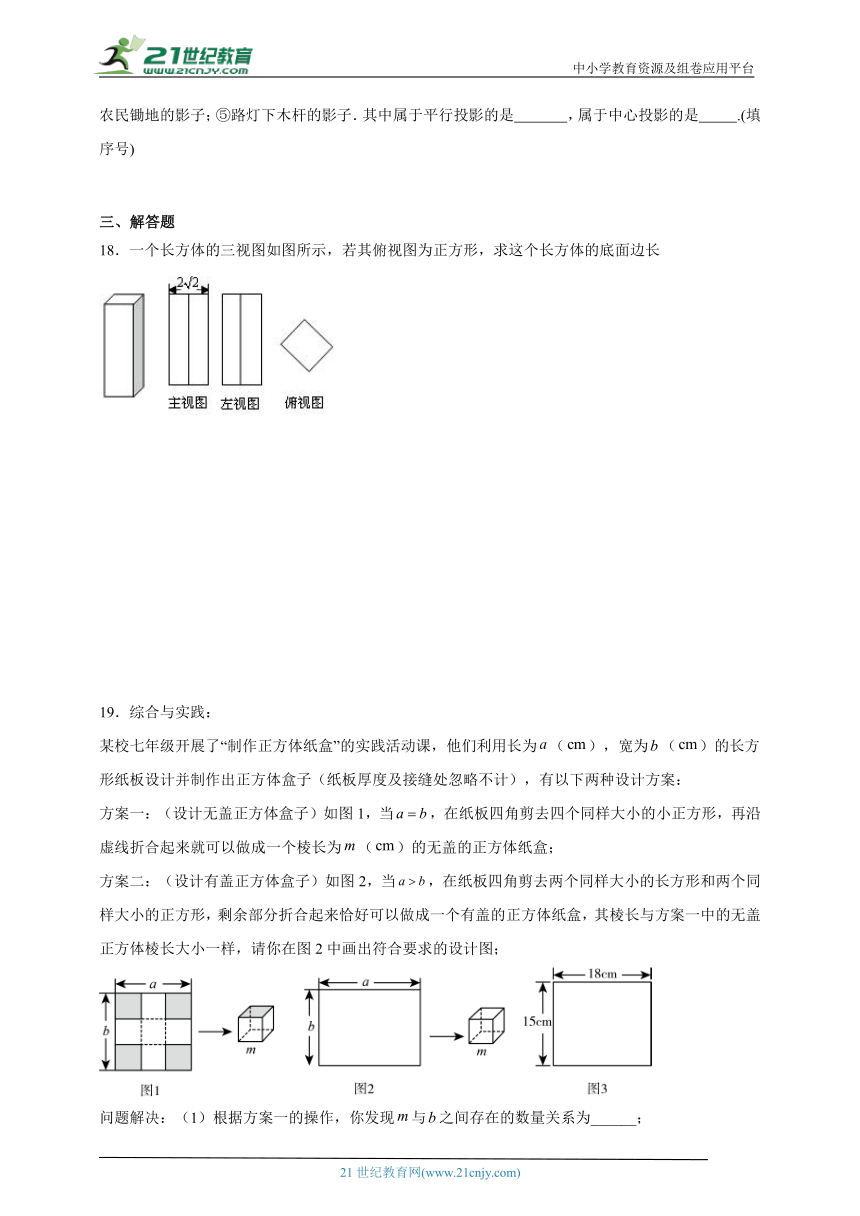
18.一个长方体的三视图如图所示,若其俯视图为正方形,求这个长方体的底面边长
19.综合与实践:
某校七年级开展了“制作正方体纸盒”的实践活动课,他们利用长为(),宽为()的长方形纸板设计并制作出正方体盒子(纸板厚度及接缝处忽略不计),有以下两种设计方案:
方案一:(设计无盖正方体盒子)如图1,当,在纸板四角剪去四个同样大小的小正方形,再沿虚线折合起来就可以做成一个棱长为()的无盖的正方体纸盒;
方案二:(设计有盖正方体盒子)如图2,当,在纸板四角剪去两个同样大小的长方形和两个同样大小的正方形,剩余部分折合起来恰好可以做成一个有盖的正方体纸盒,其棱长与方案一中的无盖正方体棱长大小一样,请你在图2中画出符合要求的设计图;
问题解决:(1)根据方案一的操作,你发现与之间存在的数量关系为______;
(2)根据方案二的操作,你发现与之间存在的数量关系为______;
实际应用:(3)如图3,将一张长,宽的纸板剪掉部分长方形或正方形后,剩余部分恰好可以分成六个同样大小的正方形,且折合起来得到一个有盖的正方体纸盒,求该正方体纸盒表面积的最大值.
20.在上题中若正三角形的边长为6,求该几何体的表面积.
21.在学习完投影的知识后,小张同学立刻进行了实践,他利用所学知识测量操场旗杆的高度.
(1)如图,请你根据小张()在阳光下的投影(),画出此时旗杆()在阳光下的投影.
(2)已知小张的身高为,在同一时刻测得小张和旗杆的投影长分别为和,求旗杆的高度.
22.下列第二行的哪种几何体的表面能展开成第一行的平面图形?请对应连线.
23.分别画出下面两个几何体从三个方向看到的平面图形.
24.如图,这是某些几何体的表面展开图,请分别写出几何体的名称.
《第三十二章投影与视图》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C A A B B B D C D
题号 11 12
答案 C D
1.C
【分析】要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,连接AB,根据展开所得扇形的弧长等于圆锥底面圆的周长求得扇形的圆心角,进而解三角形即可求解.
【详解】解:根据题意,将该圆锥展开如下图所示的扇形,
则线段AB就是蚂蚁爬行的最短距离.
∵点B是母线PA的中点,,
∴,
∵圆锥的底面圆的周长=扇形的弧长,
又∵圆锥底面半径为1,
∴扇形的弧长=圆锥底面周长,即,扇形的半径=圆锥的母线=PA=4,
由弧长公式可得:
∴扇形的圆心角,
在Rt△APB中,由勾股定理可得:,
所以 蚂蚁爬行的最短路程为,
故选:C.
【点睛】.本题考查平面展开--最短路径问题、圆的周长计算公式、弧长计算公式,勾股定理等知识,解题的关键是“化曲为直”,将立体图形转化为平面图形.
2.C
【详解】从俯视图可以看出直观图的下面部分为长方体,上面部分为圆柱,且与下面的长方体的高度相同.只有选项C符合要求,故选C.
3.A
【详解】∵将一张边长为3的正方形纸片按虚线裁剪后,恰好围成一个底面是正三角形的棱柱,
∴这个正三角形的底面边长为1,高为.
∴侧面积为长为3,宽为的长方形,面积为.
故选A.
考点:剪纸问题,展开图折叠成几何体,等边三角形的性质,勾股定理.
4.A
【详解】试题解析:从正面看到的图形第二列是两层,第一列和第三列都是一层.
故选A.
5.B
【详解】、解:由三视图可知此几何体为圆锥,
∴圆锥的底面半径为3,母线长为5,
∵圆锥的底面周长等于圆锥的侧面展开扇形的弧长,
∴圆锥的底面周长=圆锥的侧面展开扇形的弧长=2πr=2π×3=6π,
∴圆锥的侧面积=lr=×6π×5=15π,
故选B
6.B
【分析】拿掉若干个小立方块后保证几何体不倒掉,且三个视图仍都为3×3的正方形,所以最底下一层必须有九个小立方块,这样能保证俯视图仍为3×3的正方形,为保证正视图与左视图也为3×3的正方形,所以上面两层必须保留对角线上的共六个立方块,即可知最多能拿掉小立方块的个数.
【详解】根据题意,拿掉若干个小立方块后,三个视图仍都为3×3的正方形,
则最多能拿掉小立方块的个数为6+6=12个,
故选B.
【点睛】本题考查了简单几何体的三视图,掌握定义是关键.解决此类图的关键是由立体图形得到三视图;掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”则更易解决此类问题.
7.B
【分析】本题考查了位似变换、中心投影,中心投影得到的阴影与原图形是位似图形,两个位似图形的位似比等于它们的对应边的比,根据、,可得位似比为,因为,所以边的中心投影的长为.
【详解】解:三角板与阴影是位似图形,
它们的位似比为,
,
解得:.
故选: B.
8.D
【分析】根据位似图形的性质得出相似比为1:2,对应边的比为1:2,即可得出投影三角形的对应边长.
【详解】∵位似图形由三角尺与其灯光照射下的中心投影组成,相似比为1:2,三角尺的一边长为5cm,∴投影三角形的对应边长为:510(cm).
故选D.
【点睛】本题考查了位似图形的性质以及中心投影的应用,根据对应边的比为1:2,再得出投影三角形的对应边长是解决问题的关键.
9.C
【分析】正投影即投影线垂直于顶面产生的投影,据此直接选择即可.
【详解】光线由上向下照射,此正五棱柱的正投影是
故选:C.
【点睛】此题考查平行投影,解题关键此五棱柱的正投影与顶面的形状大小完全相同.
10.D
【分析】根据正方体的展开图的11种不同情况进行判断即可.
【详解】解:正方体展开图的11种情况可分为“1﹣4﹣1型”6种,“2﹣3﹣1型”3种,“2﹣2﹣2型”1种,“3﹣3型”1种,
因此选项D符合题意,
故选:D.
【点睛】本题考查正方体的展开图,理解和掌握正方体的展开图的11种不同情况,是正确判断的前提.
11.C
【分析】(1)A选项通过想象可以得出两个黑色实心圆在对面上
(2)B选项就要根据实际图形结合空间想象快速判断出旋转后的物体中间并不是一个点
(3)C选项考虑竖向切割,截面图形是一个四边形
【详解】A、两个黑色实心圆在对面,此选项错误;
B、如图所示:
C、如图所示:
故选:C.
【点睛】主要考查了图形折叠、旋转以及切割之后所得到的立方图纸,解决这种题目的方法是要多做、多画.
12.D
【分析】根据正方体的展开图进行判断即可;
【详解】解:由正方体的展开图可知“地”字所在面相对的面上的汉字是“人”;
故选:D.
【点睛】本题主要考查正方体的展开图相对两个面上的文字,注意正方体的空间图形,从相对面入手是解题的关键.
13.
【分析】先根据三视图得到该几何体为圆锥,且圆锥的底面圆直径为2,母线长为2,再利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长,根据扇形面积公式计算圆锥的侧面积,即可.
【详解】解:根据三视图易得此几何体为圆锥,由题意得底面直径为2,母线长为2,
∴圆锥的侧面积=.
故答案为:
【点睛】本题考查了根据三视图判断物体形状以及求圆锥的侧面积,掌握扇形的面积公式是关键.
14.
【分析】设这种圆锥的侧面展开图的圆心角度数为n,,进行解答即可得.
【详解】解: 设这种圆锥的侧面展开图的圆心角度数为n°,
故答案为:.
【点睛】本题考查了圆锥侧面展开图的圆心角,解题的关键是掌握扇形的弧长公式.
15. 远 短
【解析】略
16.逐渐变大
【分析】在灯光下,离点光源越近,影子越大;离点光源越远,影子越小,所以当发光的手电筒由远及近时,落在竖直墙面上的球的影子会逐渐变大.
【详解】解:根据中心投影的特点,可得:当发光的手电筒由远及近时,落在竖直墙面上的球的影子会逐渐变大,
故答案为逐渐变大.
【点睛】本题综合考查了中心投影的特点和规律.中心投影的特点是:①等高的物体垂直地面放置时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.②等长的物体平行于地面放置时,在灯光下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
17. ①③④ ②⑤
【详解】试题分析:①阳光下遮阳伞的影子,③阳光下大树的影子,④阳光下农民锄地的影子,都是太阳形成的影子,故属于平行投影;②灯光下小明读书的影子,⑤路灯下木杆的影子,都是灯光形成的影子,故属于中心投影.属于平行投影的是:①③④,属于中心投影的是②⑤.
故答案为①③④,②⑤.
点睛:此题主要考查了中心投影和平行投影的性质,解题的关键是熟知平行投影和中心投影的区别.
18.2
【详解】试题分析:由俯视图和主视图知道棱柱顶的正方形对角线长是,根据勾股定理列出方程求解即可.
试题解析:解:设底面边长为x,则x2+x2=(2)2,
解得x=2,即底面边长为2.
故答案为2.
点睛:本题主要考查了三视图的基本知识以及长方体有关计算公式.用到的知识点为:主视图反映几何体的长与高,注意物体摆放位置的不同得到主视图的形状也不同.
19.(1);(2);(3).
【分析】本题考查了正方体的展开图等知识;
(1)从而图形可以直观得出;
(2)横着4个面,竖着3个面,从而得出结果;
(3)从正方体的三类展开图可以得出结果.
【详解】解:(1)如图1,
∵,
∴;
(2)如图2,
∵,,
∴;
(3)如图3,
因为正方体的11种展开图中分为3类中,横排至少4个面,
∴正方体的棱长最大是,
∴表面积最大为:.
20.27π.
【分析】圆锥的表面积包含底面圆的面积和侧面展开图扇形的面积,等边三角形的边长是底面圆的半径,再根据圆和扇形的面积公式计算即可.
【详解】解:3×6×π+32π=27π.
【点睛】本题考查圆锥的表面积的计算,解题关键是圆锥的侧面展开图是一个扇形,扇形弧长是底面圆的周长.
21.(1)见解析
(2)旗杆的高度为.
【分析】本题考查作图应用与设计作图,设计平行投影,解题的关键是读懂题意,掌握平行投影的特征.
(1)连接,过作交于,线段即为所求;
(2)根据平行投影特征得:,即可解得答案.
【详解】(1)解:连接,过作交于,如图:
线段即为所求;
(2)解:根据题意得:,
解得,
旗杆的高度为.
22.见解析.
【分析】根据几何体的平面展开图的特征可知:(1)是五棱柱的展开图;(2)是圆锥的展开图;(3)是圆柱的展开图;(4)是正方体的展开图;(5)是两个四棱锥的展开图.
【详解】连线如下:
【点睛】本题考查了几何体的展开图,熟记常见几何体的平面展开图的特征,是解决此类问题的关键.
23.见解析.
【分析】分别从正面、左面、上面对该几何体正投影所得的图形即是主视图、左视图、俯视图.
【详解】解:的主视图:,左视图:,俯视图:;
的主视图:,左视图:,俯视图:.
【点睛】本题考查简单几何体的三视图的画法,是基础考点,掌握相关知识是解题关键.
24.图1为五棱锥,图2为五棱柱
【分析】将平面展开图与几何体的底面、侧面对应,从而判定几何体类型 .
【详解】解:图1为五棱锥,图2为五棱柱.
【点睛】本题考查几何的表面展开图,注意展开图与几何体的底面,侧面的对应是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三十二章投影与视图
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知圆锥底面半径为1,母线长为4,地面圆周上有一点A,一只蚂蚁从点A出发沿圆锥侧面运动一周后到达母线PA中点B,则蚂蚁爬行的最短路程为( )
A. B. C. D.
2.下图是直观图的三视图,它对应的直观图是下图中的( )
A.A B.B C.C D.D
3.如图,将一张边长为3的正方形纸片按虚线裁剪后恰好围成一个底面是正三角形的棱柱,则这个棱柱的侧面积为( )
A.9-3 B.9 C.9- D.9-
4.图l、2给出了一个由小立方体组成的几何体的正面看,左面看,其中小正方形中的数字表示该位置上小立方体的个数,则它的上面看不能画成( )
图1 图2
A. B. C. D.
5.如图,是某几何体的三视图及相关数据,则该几何体的侧面积是( )
A.10π B.15π C.20π D.30π
6.如图,是由27个相同的小立方块搭成的几何体,它的三个视图是3×3的正方形,若拿掉若干个小立方块(几何体不倒掉),其三个视图仍都为3×3的正方形,则最多能拿掉小立方块的个数为( )
A.10 B.12 C.15 D.18
7.如图,一块三角板与投影面平行放置,测得,,边的中心投影长为,则边的中心投影的长为( )
A. B. C. D.
8.如图,位似图形由三角尺与其在灯光照射下的中心投影组成,相似比为1:2,且三角尺一边长为5cm,则投影三角形的对应边长为( )
A.8cm B.20cm C.3.2cm D.10cm
9.把一个正五棱柱如图摆放,光线由上向下照射,此正五棱柱的正投影是( )
A. B. C. D.
10.下列四个图形中,不能作为正方体的展开图的是( )
A. B.
C. D.
11.下列说法中正确的是( ).
A.折叠①,可得到图甲所示的正方体纸盒
B.图乙所示长方形绕它的对角线所在直线旋转一周,形成的几何体是②
C.用一个平面去截图丙,截面图形可能是四边形
D.以上说法都不对
12.2022年北京冬奥会的奖牌“同心”表达了“天地合·人心同”的中华文化内涵,将这六个汉字分别写在某正方体的表面上,如图是它的一种展开图,则在原正方体中,与“地”字所在面相对的面上的汉字是( )
A.合 B.同 C.心 D.人
二、填空题
13.如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为 cm2
14.某中学开展劳动实习,学生到教具加工厂制作圆锥,他们制作的圆锥,母线长为30cm,底面圆的半径为10 cm,这种圆锥的侧面展开图的圆心角度数是 .
15.中心投影的特点是:
①等高的物体垂直地面放置时,在灯光下,离点光源近的物体它的影子短,离点光源 的物体它的影子长;
②等长的物体平行于地面放置时,在灯光下,离点光源越近,影子越长;离点光源越远,影子越 ,但不会比物体本身的长度还短.
16.如图是一个球吊在空中,当发光的手电筒由远及近时,落在竖直墙面上的球的影子会 .(填“逐渐变大”“逐渐变小”)
17.下列投影:①阳光下遮阳伞的影子;②灯光下小明读书的影子;③阳光下大树的影子;④阳光下农民锄地的影子;⑤路灯下木杆的影子.其中属于平行投影的是 ,属于中心投影的是 .(填序号)
三、解答题
18.一个长方体的三视图如图所示,若其俯视图为正方形,求这个长方体的底面边长
19.综合与实践:
某校七年级开展了“制作正方体纸盒”的实践活动课,他们利用长为(),宽为()的长方形纸板设计并制作出正方体盒子(纸板厚度及接缝处忽略不计),有以下两种设计方案:
方案一:(设计无盖正方体盒子)如图1,当,在纸板四角剪去四个同样大小的小正方形,再沿虚线折合起来就可以做成一个棱长为()的无盖的正方体纸盒;
方案二:(设计有盖正方体盒子)如图2,当,在纸板四角剪去两个同样大小的长方形和两个同样大小的正方形,剩余部分折合起来恰好可以做成一个有盖的正方体纸盒,其棱长与方案一中的无盖正方体棱长大小一样,请你在图2中画出符合要求的设计图;
问题解决:(1)根据方案一的操作,你发现与之间存在的数量关系为______;
(2)根据方案二的操作,你发现与之间存在的数量关系为______;
实际应用:(3)如图3,将一张长,宽的纸板剪掉部分长方形或正方形后,剩余部分恰好可以分成六个同样大小的正方形,且折合起来得到一个有盖的正方体纸盒,求该正方体纸盒表面积的最大值.
20.在上题中若正三角形的边长为6,求该几何体的表面积.
21.在学习完投影的知识后,小张同学立刻进行了实践,他利用所学知识测量操场旗杆的高度.
(1)如图,请你根据小张()在阳光下的投影(),画出此时旗杆()在阳光下的投影.
(2)已知小张的身高为,在同一时刻测得小张和旗杆的投影长分别为和,求旗杆的高度.
22.下列第二行的哪种几何体的表面能展开成第一行的平面图形?请对应连线.
23.分别画出下面两个几何体从三个方向看到的平面图形.
24.如图,这是某些几何体的表面展开图,请分别写出几何体的名称.
《第三十二章投影与视图》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C A A B B B D C D
题号 11 12
答案 C D
1.C
【分析】要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,连接AB,根据展开所得扇形的弧长等于圆锥底面圆的周长求得扇形的圆心角,进而解三角形即可求解.
【详解】解:根据题意,将该圆锥展开如下图所示的扇形,
则线段AB就是蚂蚁爬行的最短距离.
∵点B是母线PA的中点,,
∴,
∵圆锥的底面圆的周长=扇形的弧长,
又∵圆锥底面半径为1,
∴扇形的弧长=圆锥底面周长,即,扇形的半径=圆锥的母线=PA=4,
由弧长公式可得:
∴扇形的圆心角,
在Rt△APB中,由勾股定理可得:,
所以 蚂蚁爬行的最短路程为,
故选:C.
【点睛】.本题考查平面展开--最短路径问题、圆的周长计算公式、弧长计算公式,勾股定理等知识,解题的关键是“化曲为直”,将立体图形转化为平面图形.
2.C
【详解】从俯视图可以看出直观图的下面部分为长方体,上面部分为圆柱,且与下面的长方体的高度相同.只有选项C符合要求,故选C.
3.A
【详解】∵将一张边长为3的正方形纸片按虚线裁剪后,恰好围成一个底面是正三角形的棱柱,
∴这个正三角形的底面边长为1,高为.
∴侧面积为长为3,宽为的长方形,面积为.
故选A.
考点:剪纸问题,展开图折叠成几何体,等边三角形的性质,勾股定理.
4.A
【详解】试题解析:从正面看到的图形第二列是两层,第一列和第三列都是一层.
故选A.
5.B
【详解】、解:由三视图可知此几何体为圆锥,
∴圆锥的底面半径为3,母线长为5,
∵圆锥的底面周长等于圆锥的侧面展开扇形的弧长,
∴圆锥的底面周长=圆锥的侧面展开扇形的弧长=2πr=2π×3=6π,
∴圆锥的侧面积=lr=×6π×5=15π,
故选B
6.B
【分析】拿掉若干个小立方块后保证几何体不倒掉,且三个视图仍都为3×3的正方形,所以最底下一层必须有九个小立方块,这样能保证俯视图仍为3×3的正方形,为保证正视图与左视图也为3×3的正方形,所以上面两层必须保留对角线上的共六个立方块,即可知最多能拿掉小立方块的个数.
【详解】根据题意,拿掉若干个小立方块后,三个视图仍都为3×3的正方形,
则最多能拿掉小立方块的个数为6+6=12个,
故选B.
【点睛】本题考查了简单几何体的三视图,掌握定义是关键.解决此类图的关键是由立体图形得到三视图;掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”则更易解决此类问题.
7.B
【分析】本题考查了位似变换、中心投影,中心投影得到的阴影与原图形是位似图形,两个位似图形的位似比等于它们的对应边的比,根据、,可得位似比为,因为,所以边的中心投影的长为.
【详解】解:三角板与阴影是位似图形,
它们的位似比为,
,
解得:.
故选: B.
8.D
【分析】根据位似图形的性质得出相似比为1:2,对应边的比为1:2,即可得出投影三角形的对应边长.
【详解】∵位似图形由三角尺与其灯光照射下的中心投影组成,相似比为1:2,三角尺的一边长为5cm,∴投影三角形的对应边长为:510(cm).
故选D.
【点睛】本题考查了位似图形的性质以及中心投影的应用,根据对应边的比为1:2,再得出投影三角形的对应边长是解决问题的关键.
9.C
【分析】正投影即投影线垂直于顶面产生的投影,据此直接选择即可.
【详解】光线由上向下照射,此正五棱柱的正投影是
故选:C.
【点睛】此题考查平行投影,解题关键此五棱柱的正投影与顶面的形状大小完全相同.
10.D
【分析】根据正方体的展开图的11种不同情况进行判断即可.
【详解】解:正方体展开图的11种情况可分为“1﹣4﹣1型”6种,“2﹣3﹣1型”3种,“2﹣2﹣2型”1种,“3﹣3型”1种,
因此选项D符合题意,
故选:D.
【点睛】本题考查正方体的展开图,理解和掌握正方体的展开图的11种不同情况,是正确判断的前提.
11.C
【分析】(1)A选项通过想象可以得出两个黑色实心圆在对面上
(2)B选项就要根据实际图形结合空间想象快速判断出旋转后的物体中间并不是一个点
(3)C选项考虑竖向切割,截面图形是一个四边形
【详解】A、两个黑色实心圆在对面,此选项错误;
B、如图所示:
C、如图所示:
故选:C.
【点睛】主要考查了图形折叠、旋转以及切割之后所得到的立方图纸,解决这种题目的方法是要多做、多画.
12.D
【分析】根据正方体的展开图进行判断即可;
【详解】解:由正方体的展开图可知“地”字所在面相对的面上的汉字是“人”;
故选:D.
【点睛】本题主要考查正方体的展开图相对两个面上的文字,注意正方体的空间图形,从相对面入手是解题的关键.
13.
【分析】先根据三视图得到该几何体为圆锥,且圆锥的底面圆直径为2,母线长为2,再利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长,根据扇形面积公式计算圆锥的侧面积,即可.
【详解】解:根据三视图易得此几何体为圆锥,由题意得底面直径为2,母线长为2,
∴圆锥的侧面积=.
故答案为:
【点睛】本题考查了根据三视图判断物体形状以及求圆锥的侧面积,掌握扇形的面积公式是关键.
14.
【分析】设这种圆锥的侧面展开图的圆心角度数为n,,进行解答即可得.
【详解】解: 设这种圆锥的侧面展开图的圆心角度数为n°,
故答案为:.
【点睛】本题考查了圆锥侧面展开图的圆心角,解题的关键是掌握扇形的弧长公式.
15. 远 短
【解析】略
16.逐渐变大
【分析】在灯光下,离点光源越近,影子越大;离点光源越远,影子越小,所以当发光的手电筒由远及近时,落在竖直墙面上的球的影子会逐渐变大.
【详解】解:根据中心投影的特点,可得:当发光的手电筒由远及近时,落在竖直墙面上的球的影子会逐渐变大,
故答案为逐渐变大.
【点睛】本题综合考查了中心投影的特点和规律.中心投影的特点是:①等高的物体垂直地面放置时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.②等长的物体平行于地面放置时,在灯光下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
17. ①③④ ②⑤
【详解】试题分析:①阳光下遮阳伞的影子,③阳光下大树的影子,④阳光下农民锄地的影子,都是太阳形成的影子,故属于平行投影;②灯光下小明读书的影子,⑤路灯下木杆的影子,都是灯光形成的影子,故属于中心投影.属于平行投影的是:①③④,属于中心投影的是②⑤.
故答案为①③④,②⑤.
点睛:此题主要考查了中心投影和平行投影的性质,解题的关键是熟知平行投影和中心投影的区别.
18.2
【详解】试题分析:由俯视图和主视图知道棱柱顶的正方形对角线长是,根据勾股定理列出方程求解即可.
试题解析:解:设底面边长为x,则x2+x2=(2)2,
解得x=2,即底面边长为2.
故答案为2.
点睛:本题主要考查了三视图的基本知识以及长方体有关计算公式.用到的知识点为:主视图反映几何体的长与高,注意物体摆放位置的不同得到主视图的形状也不同.
19.(1);(2);(3).
【分析】本题考查了正方体的展开图等知识;
(1)从而图形可以直观得出;
(2)横着4个面,竖着3个面,从而得出结果;
(3)从正方体的三类展开图可以得出结果.
【详解】解:(1)如图1,
∵,
∴;
(2)如图2,
∵,,
∴;
(3)如图3,
因为正方体的11种展开图中分为3类中,横排至少4个面,
∴正方体的棱长最大是,
∴表面积最大为:.
20.27π.
【分析】圆锥的表面积包含底面圆的面积和侧面展开图扇形的面积,等边三角形的边长是底面圆的半径,再根据圆和扇形的面积公式计算即可.
【详解】解:3×6×π+32π=27π.
【点睛】本题考查圆锥的表面积的计算,解题关键是圆锥的侧面展开图是一个扇形,扇形弧长是底面圆的周长.
21.(1)见解析
(2)旗杆的高度为.
【分析】本题考查作图应用与设计作图,设计平行投影,解题的关键是读懂题意,掌握平行投影的特征.
(1)连接,过作交于,线段即为所求;
(2)根据平行投影特征得:,即可解得答案.
【详解】(1)解:连接,过作交于,如图:
线段即为所求;
(2)解:根据题意得:,
解得,
旗杆的高度为.
22.见解析.
【分析】根据几何体的平面展开图的特征可知:(1)是五棱柱的展开图;(2)是圆锥的展开图;(3)是圆柱的展开图;(4)是正方体的展开图;(5)是两个四棱锥的展开图.
【详解】连线如下:
【点睛】本题考查了几何体的展开图,熟记常见几何体的平面展开图的特征,是解决此类问题的关键.
23.见解析.
【分析】分别从正面、左面、上面对该几何体正投影所得的图形即是主视图、左视图、俯视图.
【详解】解:的主视图:,左视图:,俯视图:;
的主视图:,左视图:,俯视图:.
【点睛】本题考查简单几何体的三视图的画法,是基础考点,掌握相关知识是解题关键.
24.图1为五棱锥,图2为五棱柱
【分析】将平面展开图与几何体的底面、侧面对应,从而判定几何体类型 .
【详解】解:图1为五棱锥,图2为五棱柱.
【点睛】本题考查几何的表面展开图,注意展开图与几何体的底面,侧面的对应是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
