30.2二次函数的图像和性质同步练习(含解析)
文档属性
| 名称 | 30.2二次函数的图像和性质同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
30.2二次函数的图像和性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.抛物线的对称轴是直线( )
A.x=2 B.x=0 C.y=0 D.y=2
2.为搞好环保,某公司准备修建一个长方体的污水处理池,池底矩形的周长为,则池底的最大面积是( )
A. B. C. D.
3.如图,在菱形中,,,矩形的四个顶点分别在菱形的四边上,,则矩形的最大面积为( )
A. B. C. D.
4.如图是二次函数的图象,则a的值是( )
A. B. C.1 D.1或
5.抛物线经过点(m,3),则代数式的值为( )
A.0 B.1 C.2 D.3
6.若点P(m,n)在抛物线y=ax2(a≠0)上,则下列各点在抛物线上的是( )
A. B. C. D.
7.关于的方程有两个不相等的实根、,若,则的最大值是( )
A.1 B. C. D.2
8.二次函数y=(2x-1)2+2的顶点的坐标是( )
A.(1,2) B.(1,-2) C.(,2) D.(-,-2)
9.已知抛物线如图所示,有下列命题:①;②对称轴为直线;③若抛物线经过点,则;④顶点坐标是.其中真命题的个数是( )
A.1 B.2 C.3 D.4
10.已知二次函数y=-x2+2x,当-1<x<a时,y随x的增大而增大,则实数a的取值范围是 ( )
A.a>1 B.-1<a≤1 C.a>0 D.-1<a<2
11.抛物线y=ax2和y=-ax2在同一坐标系内,下面结论正确的是( )
A.顶点坐标不同 B.对称轴相同
C.开口方向一致 D.都有最低点
12.已知二次函数y=-2x2+4x-3,如果y随x的增大而减小,那么x的取值范围是( )
A. B. C. D.
二、填空题
13.二次函数y=3x2-3的图象开口向 ,顶点坐标为 ,对称轴为 ,当x>0时,y随x的增大而 ;当x<0时,y随x的增大而 .因为a=3>0,所以y有最 值,当x= 时,y的最 值是 .
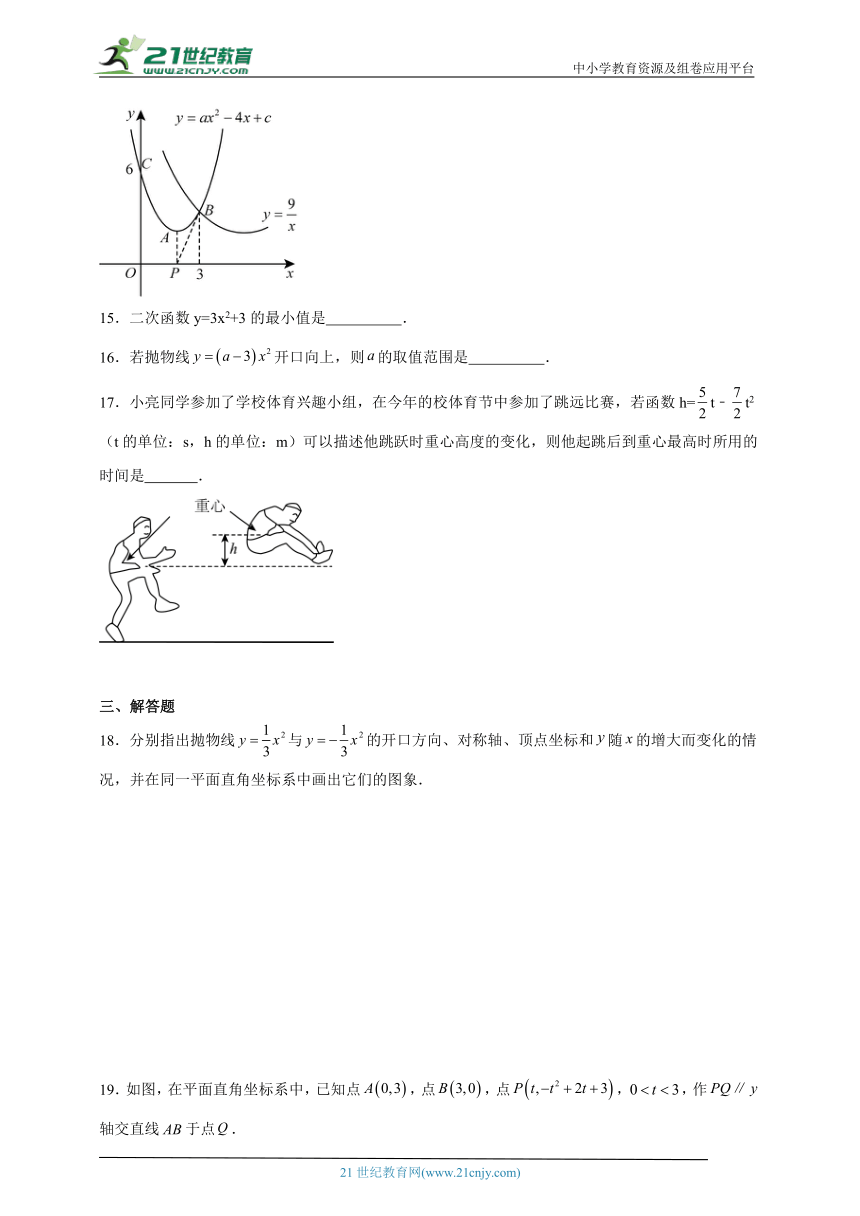
14.如图,已知抛物线y=ax2-4x+c(a≠0)与反比例函数y=的图象相交于B点,且B点的横坐标为3,抛物线与y轴交于点C(0,6),A是抛物线y=ax2-4x+c的顶点,P点是x轴上一动点,当PA+PB最小时,P点的坐标为 .
15.二次函数y=3x2+3的最小值是 .
16.若抛物线开口向上,则的取值范围是 .
17.小亮同学参加了学校体育兴趣小组,在今年的校体育节中参加了跳远比赛,若函数h=t﹣t2(t的单位:s,h的单位:m)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是 .
三、解答题
18.分别指出抛物线与的开口方向、对称轴、顶点坐标和随的增大而变化的情况,并在同一平面直角坐标系中画出它们的图象.
19.如图,在平面直角坐标系中,已知点,点,点,,作轴交直线于点.
(1)直线的解析式为______;
(2)用含的代数式表示的长为______;
(3)用含的代数式表示的面积为______;
(4)当时,的值为______;
(5)当______时,的面积最大,最大面积是______.
20.已知:抛物线的顶点坐标为(1,-4),且经过点(-2,5).
(1)求此二次函数的表达式;
(2)求此抛物线与x轴的交点坐标.
21.知识储备
在求二次函数y=ax2+bx+c(a>0)的最小值时,除了通过观察图象,还可以通过配方得到.把二次函数y=ax2+bx+c(a>0)的右边配方,得
y=ax2+bx+c
=a(x2+x)+c
=a[x2+2 x+()2﹣()2]+c
=a(x+)2+
∵a(x+)2≥0,
∴当x=﹣时,二次函数y=ax2+bx+c(a>0)的最小值为.
解决问题
(1)请你通过配方求函数y=x2+的最小值.
(2)你能否通过配方求函数y=x+(x>0)的最小值.
数学模型
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
22.如图,抛物线y=ax2+bx+c经过点A(﹣2,5),与x轴相交于B(﹣1,0),C(3,0)两点.
(1)求抛物线的函数表达式;
(2)点D在抛物线的对称轴上,且位于x轴的上方,将△BCD沿直线BD翻折得到△BC′D,若点C′恰好落在抛物线的对称轴上,求点C′和点D的坐标;
23.如图,抛物线经过点,并与x轴交于点C,点M是抛物线对称轴l上任意一点(点M,B,C三点不在同一直线上).
(1)求该抛物线的解析式;
(2)在抛物线上找出点P,使得以M,C,B,P为顶点的四边形为平行四边形,并直接写出点P的坐标.
24.指出下列抛物线的开口方向、对称轴和顶点坐标.
抛物线 开口方向 对称轴 顶点坐标
《30.2二次函数的图像和性质》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B D C D D D C C B
题号 11 12
答案 B A
1.B
【分析】根据二次函数的性质可进行求解.
【详解】解:由抛物线可知:对称轴为直线;
故选B.
【点睛】本题主要考查二次函数的性质,熟练掌握二次函数的性质是解题的关键.
2.B
【分析】先求出最大面积的表达式,再运用性质求解.
【详解】设矩形的一边长为xm,则其邻边为(50 x)m,若面积为S,则
S=x(50 x)= x2+50x= (x 25)2+625,
∵ 1<0,
∴S有最大值.
当x=25时,最大值为625.
故答案选B.
【点睛】本题考查了二次函数的应用,解题的关键是熟练的掌握二次函数的应用.
3.D
【分析】设,则,连接AC,交于点E,根据菱形的性质,矩形的性质,勾股定理计算,设矩形的面积为S,构造二次函数,根据二次函数的最值求解即可.
【详解】设,
因为四边形是菱形,,,
所以,
连接AC,交于点E,
因为四边形是菱形,四边形是矩形,,,
所以,
因为,
所以,
所以,
所以
设矩形的面积为S,
所以,
所以当x=3时,S的面积最大,最大值为,
故选D.
【点睛】本题考查了菱形的性质,矩形的性质,等腰三角形的三线合一,勾股定理,二次函数的最值,熟练掌握菱形的性质,勾股定理,二次函数的性质是解题的关键.
4.C
【分析】根据二次函数图像开口向上知a>0,再根据函数图像经过原点,将(0,0)代入解析式即可求得a值.
【详解】解:由图像可知,二次函数图像经过原点,
将(0,0)代入中得:,
解得:,
又因为二次函数图像开口向上,所以>0,
∴,
故选:C.
【点睛】本题考查了二次函数的图像与性质、解一元二次方程,解答的关键是掌握函数图像上的点与函数关系,以及开口方向问题.
5.D
【分析】将点(m,3)代入代数式中即可得到结果.
【详解】解:将点(m,3)代入中得,
,
故代数式的值为3,
故选:D.
【点睛】本题考查代数式的值,根据函数图象经过的点求函数解析式,能够掌握属性结合思想是解决本题的关键.
6.D
【详解】解法一:∵点P(m,n)在抛物线(a≠0)上,
∴,把x=m代入得,也不等于n-1,故点(m,n+1)和点(m,n-1)不在抛物线上,A,C不合题意;
把x=m+1代入得,故点(m+1,n)不在抛物线上,B不合题意;
把x=m-1代入得,故点(m-1,n)在抛物线上,D符合题意.
解法二:抛物线可看作是抛物线向左平移1个单位长度得到的,点P(m,n)向左平移1个单位长度后所得的点的坐标为(m-1,n).
7.D
【分析】根据一元二次方程根与系数的关系,求得两根之和和两根之积,再根据两根关系,求得系数的关系,代入代数式,配方法化简求值即可.
【详解】解:由方程有两个不相等的实根、
可得,,,
∵,可得,,即
化简得
则
故最大值为
故选D
【点睛】此题考查了一元二次方程根与系数的关系,涉及了配方法求解代数式的最大值,根据一元二次方程根与系数的关系得到系数的关系是解题的关键.
8.C
【详解】试题分析:二次函数y=(2x-1)+2即的顶点坐标为(,2)
考点:二次函数
点评:本题考查二次函数的顶点坐标,考生要掌握二次函数的顶点式与其顶点坐标的关系
9.C
【分析】根据图象和二次函数的性质,逐项判断即可.
【详解】解:由抛物线开口向上知,故①是真命题;
∵抛物线解析式为,
∴对称轴为直线,故②是真命题;
∵,线开口向上,对称轴为直线,
∴,故③是假命题;
∵抛物线解析式为,
∴抛物线顶点坐标是,故④是真命题;
∴真命题有:①②④,共3个;
故选:C.
【点睛】本题考查命题与定理,以及二次函数相关的性质,解题的关键是掌握二次函数相关的性质.
10.B
【详解】试题解析:由题可知,二次函数开口向下,对称轴为 ,所以在对称轴的左侧, 随 的增大而增大,那么 ,又 ,所以取值范围是 .
故本题应选B.
11.B
【分析】根据(a)的图像与特点即可判断.
【详解】∵(a)的图像都是关于y轴对称,抛物线的顶点都是原点,故选B.
【点睛】此题主要考查(a)的函数特点,解题的关键是熟知这类函数的图像与特点.
12.A
【分析】把抛物线化为顶点式可求得开口方向及对称轴,再利用增减性可得到关于x的不等式,可求得答案.
【详解】∵y=-2x2+4x-3=-2(x-1)2-1,
∴抛物线开口向下,对称轴为x=1,
∴当x≥1时,y随x的增大而减小,
故选A.
【点睛】本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,对称轴为x=h,顶点坐标为(h,k).
13. 上 (0,-3) y轴 增大 减小 小 0 小 -3.
【详解】二次函数y=3x2-3中k=3,所以开口向上,顶点坐标(0,-3),对称轴为y轴,当x>0时,y随x的增大而增大;当x<0时,y随x的增大而减小.因为a=3>0,所以y有最小值,当x=0时,y的最小值是-3.
故答案是:上, (0,-3) ,y轴, 增大,减小,小,0, 小,-3.
14.(,0)
【分析】根据题意作出合适的辅助线,然后求出点B的坐标,从而可以求得二次函数解析式,然后求出点A的坐标,进而求得A'的坐标,从而可以求得直线A'B的函数解析式,进而求得与x轴的交点,从而可以解答本题
【详解】解:作点A关于x轴的对称点A',连接A'B,则A'B与x轴的交点即为所求,
∵抛物线y=ax2-4x+c(a0)与反比例函数y= 的图象相交于点B,且B点的横坐标为3,抛物线与y轴交于点C(0,6),
∴点B(3,3),
∴
解得,
∴y=x2-4x+6=(x-2)2+2
∴点A的坐标为(2,2),
∴点A'的坐标为(2,-2),
设过点A'(2,-2)和点B(3,3)的直线解析式为y=mx+n
∴
∴直线A'B的函数解析式为y=5x-12,
令y=0,则0=5x-12得x=,
故答案为()
【点睛】本题考查反比例函数图象上点的坐标特征、二次函数的性质、二次函数图象上点的坐标特征、最短路径问题,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
15.3.
【分析】根据二次函数的性质求出函数的最小值即可.
【详解】解:∵y=3x2+3=3(x+0)2+3,
∴顶点坐标为(0,3).
∴该函数的最小值是3.
故答案为:3.
【点睛】本题考查了二次函数的性质,二次函数的最值,正确的理解题意是解题的关键.
16.a>3.
【分析】根据二次函数的性质,图象开口向上,则二次项系数大于0可得答案.
【详解】解:因为抛物线的开口向上,
所以a-3>0,即a>3.
故答案为a>3.
【点睛】本题主要考查了二次函数的性质.用到的知识点:对于二次函数y=ax2(a≠0)来说,当a>0时,抛物线开口向上;当a<0时,抛物线开口向下.
17.
【分析】重心最高点,就是求这个二次函数的顶点,将二次函数化为顶点式,由此即可得.
【详解】
由二次函数的性质可知,当时,h取得最大值
故答案为:.
【点睛】本题考查了二次函数的性质,掌握二次函数的性质是解题关键.
18.两个函数的对称轴都是轴,顶点坐标都是,,,故函数图象开口向上,时,随的增大而增大,时,随的增大而减小;,,故函数图象开口向下,时,随的增大而增大,时,随的增大而减小;图见解析
【分析】根据函数的图象及性质解答.
【详解】两个函数的对称轴都是轴,顶点坐标都是,
,,故函数图象开口向上,时,随的增大而增大,时,随的增大而减小;
,,故函数图象开口向下,时,随的增大而增大,时,随的增大而减小;
二次函数的与的部分对应值如表:
… 0 1 2 3 …
… 3 0 3 …
… 0 …
根据表格描点绘图:
【点睛】此题考查了二次函数的图象及性质,熟练掌握各类型的二次函数的图象及性质是解题的关键.
19.(1)
(2)
(3)
(4)
(5),
【分析】本题考查一次函数与几何的应用,二次函数的性质.
(1)利用待定系数法求解即可;
(2)根据,,求出,即可求解;
(3)利用的面积为列式即可求解;
(4)根据当和的共底边上的高相等时,,两三角形的高之和为,即可解答;
(5)根据列出关系式,利用二次函数的性质即可解答.
【详解】(1)解:点,点,
设直线的解析式为,则,
解得:,
直线的解析式为;
(2)解:,,轴,
点的坐标为,
.
(3)解:.
(4)解:和共底边,
当和的共底边上的高相等时,,
当和共底边时,两三角形的高之和为,轴,
.
(5)解:,
,
当时,有最大值,最大值为.
20.(1)
(2)此抛物线与x轴的交点坐标为(3,0),(-1,0)
【分析】(1)设顶点式,然后把(-2,5)代入求出a,即可得到抛物线解析式.
(2)将(1)中的y=0,解出一元二次方程的根即可.
【详解】(1)解:设二次函数表达式为
∵ 图像经过(-2,5)
∴ 5=
∴
(2)解:令y=0,即=0
解得:x=3或x=-1
故此抛物线与x轴的交点坐标为(3,0),(-1,0)
【点睛】本题考查了抛物线与x轴的交点,待定系数法求二次函数解析式,在利用待定系数法求二次函数解析式时,要根据题目给定条件,选择恰当的方法设出解析式,也考查了二次函数的性质.
21.(1)当x=±1时,函数y=x2+的最小值为2;(2)当x=1时,y=x+(x>0)的最小值为2;数学模型:该矩形的长为时,它的周长最小,最小值是4.
【分析】(1)根据完全平方公式,进行配方得,即可得到最小值;
(2) 根据完全平方公式,进行配方得,即可得到最小值;
数学模型:设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+)(x>0),根据完全平方公式,进行配方得到y=2[(﹣)2+2]=2(﹣)2+4,即可求出答案.
【详解】(1)
=
=
∵,
∴当x=±1时,函数y=x2+的最小值为2;
(2)y=x+
=
=()2+()2﹣2+2
=(﹣)2+2,
∵(﹣)2≥0,
∴当﹣=0时,即x=1时,y=x+(x>0)的最小值为2;
数学模型:设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+)(x>0),
y=2(x+)=2[(﹣)2+2]=2(﹣)2+4,
当﹣=0时,即x=,y有最大值4,
∴该矩形的长为时,它的周长最小,最小值是4.
【点睛】本题主要考查对完全平方公式,二次函数的最值,配方法的应用,能熟练地运用学过的性质进行计算是解本题的关键.
22.(1)y=x2﹣2x﹣3;(2)点C′的坐标为(1,2),点D的坐标为(1,)
【分析】(1)根据抛物线经过点,与轴相交于,两点,利用待定系数法求得该抛物线的解析式即可;
(2)先确定二次函数对称轴,BC长度,根据题意和翻折的性质,得到B C′长度,利用三角函数求出∠C′BC,再根据角平分线求出∠DBC,解直角三角形可以求得点和点的坐标,本题得以解决.
【详解】解:(1)∵抛物线y=ax2+bx+c经过点A(﹣2,5),与x轴相交于B(﹣1,0),C(3,0)两点,
∴,得,
即抛物线的函数表达式是y=x2﹣2x﹣3;
(2)∵与x轴相交于B(﹣1,0),C(3,0)两点,
∴BC=3﹣(﹣1)=3+1=4,该抛物线的对称轴是直线x==1,
设抛物线的对称轴与x轴的交点为H,
则点H的坐标为(1,0),
∴BH=2,
∵将△BCD沿直线BD翻折得到△BC′D,点C′恰好落在抛物线的对称轴上,
∴BC=BC′=4,∠C′HB=90°,∠C′BD=∠DBC,
∴OC′==2,cos∠C′BH===,
∴C′的坐标为(1,2),∠C′BH=60°,
∴∠DBC=30°,
∵BH=2,∠DBH=30°,
∴OD=BH tan30°=2×=,
∴点D的坐标为(1,),
由上可得,点C′的坐标为(1,2),点D的坐标为(1,).
【点睛】本题考查待定系数法求抛物线解析式,图形翻折变化、二次函数的性质、特殊角的三角函数值,解答本题的关键是明确题意,利用数形结合的思想解答.
23.(1)y=x2-x-2;(2)点P坐标为或或.
【分析】(1)利用待定系数法求二次函数的表达式;
(2)分3种情况:①如图1中,当四边形PCBM是平行四边形时;②如图2中,当四边形PMCB是平行四边形时;③当BC为对角线时.利用平移变换以及平行四边形的性质解决问题即可.
【详解】解:(1)把代入抛物线中,得
,解得,
∴抛物线的解析式为y=x2-x-2;
(2)∵y=x2-x-2=(x-)2-,
∴对称轴是直线x=.
①如图1,当四边形是平行四边形时,,且,
∵点B向右平移个单位到点M横坐标位置,
∴由点C向右平移个单位到点P横坐标位置,
∵点,
∴,
当时,,
∴;
②如图2中,当四边形是平行四边形时,
∵点C向左平移2个单位到B横坐标,
∴点M向左平移2个单位到点P横坐标,
∴点P的横坐标为.
当时,,
∴;
③当为对角线时,
∵点M的横坐标为,
∴点P的横坐标为,
当时,,
∴.
综上所述,满足条件的点P坐标为或或.
【点睛】本题考查了待定系数法求函数解析式、二次函数图象上点的坐标特征、二次函数的性质、以及平行四边形的性质,解题的关键是:(1)利用待定系数法求出函数解析式;(2)分三种情形讨论求解.
24.见解析
【分析】根据二次函数的图象与性质即可得到答案.
【详解】解:根据题意可得:
抛物线 开口方向 对称轴 顶点坐标
向下 直线
向上 直线
向上 直线
向下 直线
【点睛】本题主要考查了二次函数的图象与性质,熟练掌握当时抛物线开口向上,当时抛物线开口向下,对称轴为直线,顶点坐标为,是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
30.2二次函数的图像和性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.抛物线的对称轴是直线( )
A.x=2 B.x=0 C.y=0 D.y=2
2.为搞好环保,某公司准备修建一个长方体的污水处理池,池底矩形的周长为,则池底的最大面积是( )
A. B. C. D.
3.如图,在菱形中,,,矩形的四个顶点分别在菱形的四边上,,则矩形的最大面积为( )
A. B. C. D.
4.如图是二次函数的图象,则a的值是( )
A. B. C.1 D.1或
5.抛物线经过点(m,3),则代数式的值为( )
A.0 B.1 C.2 D.3
6.若点P(m,n)在抛物线y=ax2(a≠0)上,则下列各点在抛物线上的是( )
A. B. C. D.
7.关于的方程有两个不相等的实根、,若,则的最大值是( )
A.1 B. C. D.2
8.二次函数y=(2x-1)2+2的顶点的坐标是( )
A.(1,2) B.(1,-2) C.(,2) D.(-,-2)
9.已知抛物线如图所示,有下列命题:①;②对称轴为直线;③若抛物线经过点,则;④顶点坐标是.其中真命题的个数是( )
A.1 B.2 C.3 D.4
10.已知二次函数y=-x2+2x,当-1<x<a时,y随x的增大而增大,则实数a的取值范围是 ( )
A.a>1 B.-1<a≤1 C.a>0 D.-1<a<2
11.抛物线y=ax2和y=-ax2在同一坐标系内,下面结论正确的是( )
A.顶点坐标不同 B.对称轴相同
C.开口方向一致 D.都有最低点
12.已知二次函数y=-2x2+4x-3,如果y随x的增大而减小,那么x的取值范围是( )
A. B. C. D.
二、填空题
13.二次函数y=3x2-3的图象开口向 ,顶点坐标为 ,对称轴为 ,当x>0时,y随x的增大而 ;当x<0时,y随x的增大而 .因为a=3>0,所以y有最 值,当x= 时,y的最 值是 .
14.如图,已知抛物线y=ax2-4x+c(a≠0)与反比例函数y=的图象相交于B点,且B点的横坐标为3,抛物线与y轴交于点C(0,6),A是抛物线y=ax2-4x+c的顶点,P点是x轴上一动点,当PA+PB最小时,P点的坐标为 .
15.二次函数y=3x2+3的最小值是 .
16.若抛物线开口向上,则的取值范围是 .
17.小亮同学参加了学校体育兴趣小组,在今年的校体育节中参加了跳远比赛,若函数h=t﹣t2(t的单位:s,h的单位:m)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是 .
三、解答题
18.分别指出抛物线与的开口方向、对称轴、顶点坐标和随的增大而变化的情况,并在同一平面直角坐标系中画出它们的图象.
19.如图,在平面直角坐标系中,已知点,点,点,,作轴交直线于点.
(1)直线的解析式为______;
(2)用含的代数式表示的长为______;
(3)用含的代数式表示的面积为______;
(4)当时,的值为______;
(5)当______时,的面积最大,最大面积是______.
20.已知:抛物线的顶点坐标为(1,-4),且经过点(-2,5).
(1)求此二次函数的表达式;
(2)求此抛物线与x轴的交点坐标.
21.知识储备
在求二次函数y=ax2+bx+c(a>0)的最小值时,除了通过观察图象,还可以通过配方得到.把二次函数y=ax2+bx+c(a>0)的右边配方,得
y=ax2+bx+c
=a(x2+x)+c
=a[x2+2 x+()2﹣()2]+c
=a(x+)2+
∵a(x+)2≥0,
∴当x=﹣时,二次函数y=ax2+bx+c(a>0)的最小值为.
解决问题
(1)请你通过配方求函数y=x2+的最小值.
(2)你能否通过配方求函数y=x+(x>0)的最小值.
数学模型
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
22.如图,抛物线y=ax2+bx+c经过点A(﹣2,5),与x轴相交于B(﹣1,0),C(3,0)两点.
(1)求抛物线的函数表达式;
(2)点D在抛物线的对称轴上,且位于x轴的上方,将△BCD沿直线BD翻折得到△BC′D,若点C′恰好落在抛物线的对称轴上,求点C′和点D的坐标;
23.如图,抛物线经过点,并与x轴交于点C,点M是抛物线对称轴l上任意一点(点M,B,C三点不在同一直线上).
(1)求该抛物线的解析式;
(2)在抛物线上找出点P,使得以M,C,B,P为顶点的四边形为平行四边形,并直接写出点P的坐标.
24.指出下列抛物线的开口方向、对称轴和顶点坐标.
抛物线 开口方向 对称轴 顶点坐标
《30.2二次函数的图像和性质》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B D C D D D C C B
题号 11 12
答案 B A
1.B
【分析】根据二次函数的性质可进行求解.
【详解】解:由抛物线可知:对称轴为直线;
故选B.
【点睛】本题主要考查二次函数的性质,熟练掌握二次函数的性质是解题的关键.
2.B
【分析】先求出最大面积的表达式,再运用性质求解.
【详解】设矩形的一边长为xm,则其邻边为(50 x)m,若面积为S,则
S=x(50 x)= x2+50x= (x 25)2+625,
∵ 1<0,
∴S有最大值.
当x=25时,最大值为625.
故答案选B.
【点睛】本题考查了二次函数的应用,解题的关键是熟练的掌握二次函数的应用.
3.D
【分析】设,则,连接AC,交于点E,根据菱形的性质,矩形的性质,勾股定理计算,设矩形的面积为S,构造二次函数,根据二次函数的最值求解即可.
【详解】设,
因为四边形是菱形,,,
所以,
连接AC,交于点E,
因为四边形是菱形,四边形是矩形,,,
所以,
因为,
所以,
所以,
所以
设矩形的面积为S,
所以,
所以当x=3时,S的面积最大,最大值为,
故选D.
【点睛】本题考查了菱形的性质,矩形的性质,等腰三角形的三线合一,勾股定理,二次函数的最值,熟练掌握菱形的性质,勾股定理,二次函数的性质是解题的关键.
4.C
【分析】根据二次函数图像开口向上知a>0,再根据函数图像经过原点,将(0,0)代入解析式即可求得a值.
【详解】解:由图像可知,二次函数图像经过原点,
将(0,0)代入中得:,
解得:,
又因为二次函数图像开口向上,所以>0,
∴,
故选:C.
【点睛】本题考查了二次函数的图像与性质、解一元二次方程,解答的关键是掌握函数图像上的点与函数关系,以及开口方向问题.
5.D
【分析】将点(m,3)代入代数式中即可得到结果.
【详解】解:将点(m,3)代入中得,
,
故代数式的值为3,
故选:D.
【点睛】本题考查代数式的值,根据函数图象经过的点求函数解析式,能够掌握属性结合思想是解决本题的关键.
6.D
【详解】解法一:∵点P(m,n)在抛物线(a≠0)上,
∴,把x=m代入得,也不等于n-1,故点(m,n+1)和点(m,n-1)不在抛物线上,A,C不合题意;
把x=m+1代入得,故点(m+1,n)不在抛物线上,B不合题意;
把x=m-1代入得,故点(m-1,n)在抛物线上,D符合题意.
解法二:抛物线可看作是抛物线向左平移1个单位长度得到的,点P(m,n)向左平移1个单位长度后所得的点的坐标为(m-1,n).
7.D
【分析】根据一元二次方程根与系数的关系,求得两根之和和两根之积,再根据两根关系,求得系数的关系,代入代数式,配方法化简求值即可.
【详解】解:由方程有两个不相等的实根、
可得,,,
∵,可得,,即
化简得
则
故最大值为
故选D
【点睛】此题考查了一元二次方程根与系数的关系,涉及了配方法求解代数式的最大值,根据一元二次方程根与系数的关系得到系数的关系是解题的关键.
8.C
【详解】试题分析:二次函数y=(2x-1)+2即的顶点坐标为(,2)
考点:二次函数
点评:本题考查二次函数的顶点坐标,考生要掌握二次函数的顶点式与其顶点坐标的关系
9.C
【分析】根据图象和二次函数的性质,逐项判断即可.
【详解】解:由抛物线开口向上知,故①是真命题;
∵抛物线解析式为,
∴对称轴为直线,故②是真命题;
∵,线开口向上,对称轴为直线,
∴,故③是假命题;
∵抛物线解析式为,
∴抛物线顶点坐标是,故④是真命题;
∴真命题有:①②④,共3个;
故选:C.
【点睛】本题考查命题与定理,以及二次函数相关的性质,解题的关键是掌握二次函数相关的性质.
10.B
【详解】试题解析:由题可知,二次函数开口向下,对称轴为 ,所以在对称轴的左侧, 随 的增大而增大,那么 ,又 ,所以取值范围是 .
故本题应选B.
11.B
【分析】根据(a)的图像与特点即可判断.
【详解】∵(a)的图像都是关于y轴对称,抛物线的顶点都是原点,故选B.
【点睛】此题主要考查(a)的函数特点,解题的关键是熟知这类函数的图像与特点.
12.A
【分析】把抛物线化为顶点式可求得开口方向及对称轴,再利用增减性可得到关于x的不等式,可求得答案.
【详解】∵y=-2x2+4x-3=-2(x-1)2-1,
∴抛物线开口向下,对称轴为x=1,
∴当x≥1时,y随x的增大而减小,
故选A.
【点睛】本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,对称轴为x=h,顶点坐标为(h,k).
13. 上 (0,-3) y轴 增大 减小 小 0 小 -3.
【详解】二次函数y=3x2-3中k=3,所以开口向上,顶点坐标(0,-3),对称轴为y轴,当x>0时,y随x的增大而增大;当x<0时,y随x的增大而减小.因为a=3>0,所以y有最小值,当x=0时,y的最小值是-3.
故答案是:上, (0,-3) ,y轴, 增大,减小,小,0, 小,-3.
14.(,0)
【分析】根据题意作出合适的辅助线,然后求出点B的坐标,从而可以求得二次函数解析式,然后求出点A的坐标,进而求得A'的坐标,从而可以求得直线A'B的函数解析式,进而求得与x轴的交点,从而可以解答本题
【详解】解:作点A关于x轴的对称点A',连接A'B,则A'B与x轴的交点即为所求,
∵抛物线y=ax2-4x+c(a0)与反比例函数y= 的图象相交于点B,且B点的横坐标为3,抛物线与y轴交于点C(0,6),
∴点B(3,3),
∴
解得,
∴y=x2-4x+6=(x-2)2+2
∴点A的坐标为(2,2),
∴点A'的坐标为(2,-2),
设过点A'(2,-2)和点B(3,3)的直线解析式为y=mx+n
∴
∴直线A'B的函数解析式为y=5x-12,
令y=0,则0=5x-12得x=,
故答案为()
【点睛】本题考查反比例函数图象上点的坐标特征、二次函数的性质、二次函数图象上点的坐标特征、最短路径问题,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
15.3.
【分析】根据二次函数的性质求出函数的最小值即可.
【详解】解:∵y=3x2+3=3(x+0)2+3,
∴顶点坐标为(0,3).
∴该函数的最小值是3.
故答案为:3.
【点睛】本题考查了二次函数的性质,二次函数的最值,正确的理解题意是解题的关键.
16.a>3.
【分析】根据二次函数的性质,图象开口向上,则二次项系数大于0可得答案.
【详解】解:因为抛物线的开口向上,
所以a-3>0,即a>3.
故答案为a>3.
【点睛】本题主要考查了二次函数的性质.用到的知识点:对于二次函数y=ax2(a≠0)来说,当a>0时,抛物线开口向上;当a<0时,抛物线开口向下.
17.
【分析】重心最高点,就是求这个二次函数的顶点,将二次函数化为顶点式,由此即可得.
【详解】
由二次函数的性质可知,当时,h取得最大值
故答案为:.
【点睛】本题考查了二次函数的性质,掌握二次函数的性质是解题关键.
18.两个函数的对称轴都是轴,顶点坐标都是,,,故函数图象开口向上,时,随的增大而增大,时,随的增大而减小;,,故函数图象开口向下,时,随的增大而增大,时,随的增大而减小;图见解析
【分析】根据函数的图象及性质解答.
【详解】两个函数的对称轴都是轴,顶点坐标都是,
,,故函数图象开口向上,时,随的增大而增大,时,随的增大而减小;
,,故函数图象开口向下,时,随的增大而增大,时,随的增大而减小;
二次函数的与的部分对应值如表:
… 0 1 2 3 …
… 3 0 3 …
… 0 …
根据表格描点绘图:
【点睛】此题考查了二次函数的图象及性质,熟练掌握各类型的二次函数的图象及性质是解题的关键.
19.(1)
(2)
(3)
(4)
(5),
【分析】本题考查一次函数与几何的应用,二次函数的性质.
(1)利用待定系数法求解即可;
(2)根据,,求出,即可求解;
(3)利用的面积为列式即可求解;
(4)根据当和的共底边上的高相等时,,两三角形的高之和为,即可解答;
(5)根据列出关系式,利用二次函数的性质即可解答.
【详解】(1)解:点,点,
设直线的解析式为,则,
解得:,
直线的解析式为;
(2)解:,,轴,
点的坐标为,
.
(3)解:.
(4)解:和共底边,
当和的共底边上的高相等时,,
当和共底边时,两三角形的高之和为,轴,
.
(5)解:,
,
当时,有最大值,最大值为.
20.(1)
(2)此抛物线与x轴的交点坐标为(3,0),(-1,0)
【分析】(1)设顶点式,然后把(-2,5)代入求出a,即可得到抛物线解析式.
(2)将(1)中的y=0,解出一元二次方程的根即可.
【详解】(1)解:设二次函数表达式为
∵ 图像经过(-2,5)
∴ 5=
∴
(2)解:令y=0,即=0
解得:x=3或x=-1
故此抛物线与x轴的交点坐标为(3,0),(-1,0)
【点睛】本题考查了抛物线与x轴的交点,待定系数法求二次函数解析式,在利用待定系数法求二次函数解析式时,要根据题目给定条件,选择恰当的方法设出解析式,也考查了二次函数的性质.
21.(1)当x=±1时,函数y=x2+的最小值为2;(2)当x=1时,y=x+(x>0)的最小值为2;数学模型:该矩形的长为时,它的周长最小,最小值是4.
【分析】(1)根据完全平方公式,进行配方得,即可得到最小值;
(2) 根据完全平方公式,进行配方得,即可得到最小值;
数学模型:设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+)(x>0),根据完全平方公式,进行配方得到y=2[(﹣)2+2]=2(﹣)2+4,即可求出答案.
【详解】(1)
=
=
∵,
∴当x=±1时,函数y=x2+的最小值为2;
(2)y=x+
=
=()2+()2﹣2+2
=(﹣)2+2,
∵(﹣)2≥0,
∴当﹣=0时,即x=1时,y=x+(x>0)的最小值为2;
数学模型:设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+)(x>0),
y=2(x+)=2[(﹣)2+2]=2(﹣)2+4,
当﹣=0时,即x=,y有最大值4,
∴该矩形的长为时,它的周长最小,最小值是4.
【点睛】本题主要考查对完全平方公式,二次函数的最值,配方法的应用,能熟练地运用学过的性质进行计算是解本题的关键.
22.(1)y=x2﹣2x﹣3;(2)点C′的坐标为(1,2),点D的坐标为(1,)
【分析】(1)根据抛物线经过点,与轴相交于,两点,利用待定系数法求得该抛物线的解析式即可;
(2)先确定二次函数对称轴,BC长度,根据题意和翻折的性质,得到B C′长度,利用三角函数求出∠C′BC,再根据角平分线求出∠DBC,解直角三角形可以求得点和点的坐标,本题得以解决.
【详解】解:(1)∵抛物线y=ax2+bx+c经过点A(﹣2,5),与x轴相交于B(﹣1,0),C(3,0)两点,
∴,得,
即抛物线的函数表达式是y=x2﹣2x﹣3;
(2)∵与x轴相交于B(﹣1,0),C(3,0)两点,
∴BC=3﹣(﹣1)=3+1=4,该抛物线的对称轴是直线x==1,
设抛物线的对称轴与x轴的交点为H,
则点H的坐标为(1,0),
∴BH=2,
∵将△BCD沿直线BD翻折得到△BC′D,点C′恰好落在抛物线的对称轴上,
∴BC=BC′=4,∠C′HB=90°,∠C′BD=∠DBC,
∴OC′==2,cos∠C′BH===,
∴C′的坐标为(1,2),∠C′BH=60°,
∴∠DBC=30°,
∵BH=2,∠DBH=30°,
∴OD=BH tan30°=2×=,
∴点D的坐标为(1,),
由上可得,点C′的坐标为(1,2),点D的坐标为(1,).
【点睛】本题考查待定系数法求抛物线解析式,图形翻折变化、二次函数的性质、特殊角的三角函数值,解答本题的关键是明确题意,利用数形结合的思想解答.
23.(1)y=x2-x-2;(2)点P坐标为或或.
【分析】(1)利用待定系数法求二次函数的表达式;
(2)分3种情况:①如图1中,当四边形PCBM是平行四边形时;②如图2中,当四边形PMCB是平行四边形时;③当BC为对角线时.利用平移变换以及平行四边形的性质解决问题即可.
【详解】解:(1)把代入抛物线中,得
,解得,
∴抛物线的解析式为y=x2-x-2;
(2)∵y=x2-x-2=(x-)2-,
∴对称轴是直线x=.
①如图1,当四边形是平行四边形时,,且,
∵点B向右平移个单位到点M横坐标位置,
∴由点C向右平移个单位到点P横坐标位置,
∵点,
∴,
当时,,
∴;
②如图2中,当四边形是平行四边形时,
∵点C向左平移2个单位到B横坐标,
∴点M向左平移2个单位到点P横坐标,
∴点P的横坐标为.
当时,,
∴;
③当为对角线时,
∵点M的横坐标为,
∴点P的横坐标为,
当时,,
∴.
综上所述,满足条件的点P坐标为或或.
【点睛】本题考查了待定系数法求函数解析式、二次函数图象上点的坐标特征、二次函数的性质、以及平行四边形的性质,解题的关键是:(1)利用待定系数法求出函数解析式;(2)分三种情形讨论求解.
24.见解析
【分析】根据二次函数的图象与性质即可得到答案.
【详解】解:根据题意可得:
抛物线 开口方向 对称轴 顶点坐标
向下 直线
向上 直线
向上 直线
向下 直线
【点睛】本题主要考查了二次函数的图象与性质,熟练掌握当时抛物线开口向上,当时抛物线开口向下,对称轴为直线,顶点坐标为,是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
