30.4二次函数的应用同步练习(含解析)
文档属性
| 名称 | 30.4二次函数的应用同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
30.4二次函数的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.共享单车为市民出行带来了方便,某单车公司第一个月投放辆单车,计划第三个月投放单车辆,若第二个月的增长率是,第三个月的增长率是第二个月的两倍,那么与的函数关系是 ( )
A. B.
C. D.
2.出售某种文具盒,若每个可获利x元,一天可售出(6-x)个.当一天出售该种文具盒的总利润y最大时,x的值为( )
A.1 B.2 C.3 D.4
3.已知x为矩形的一边长,其面积为y,且, 则自变量的取值范围是( )
A. B. C.0≤x≤4 D.
4.烟花厂为热烈庆祝“十一国庆”,特别设计制作一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是,礼炮点火升空后会在最高点处引爆,则这种礼炮能上升的最大高度为( )
A.91米 B.90米 C.81米 D.80米
5.如图,四边形ABCD中,AB=AD,CE⊥BD,CE=BD.若△ABD的周长为20cm,则△BCD的面积S(cm2)与AB的长(cm)之间的函数关系式可以是( )
A. B.
C. D.
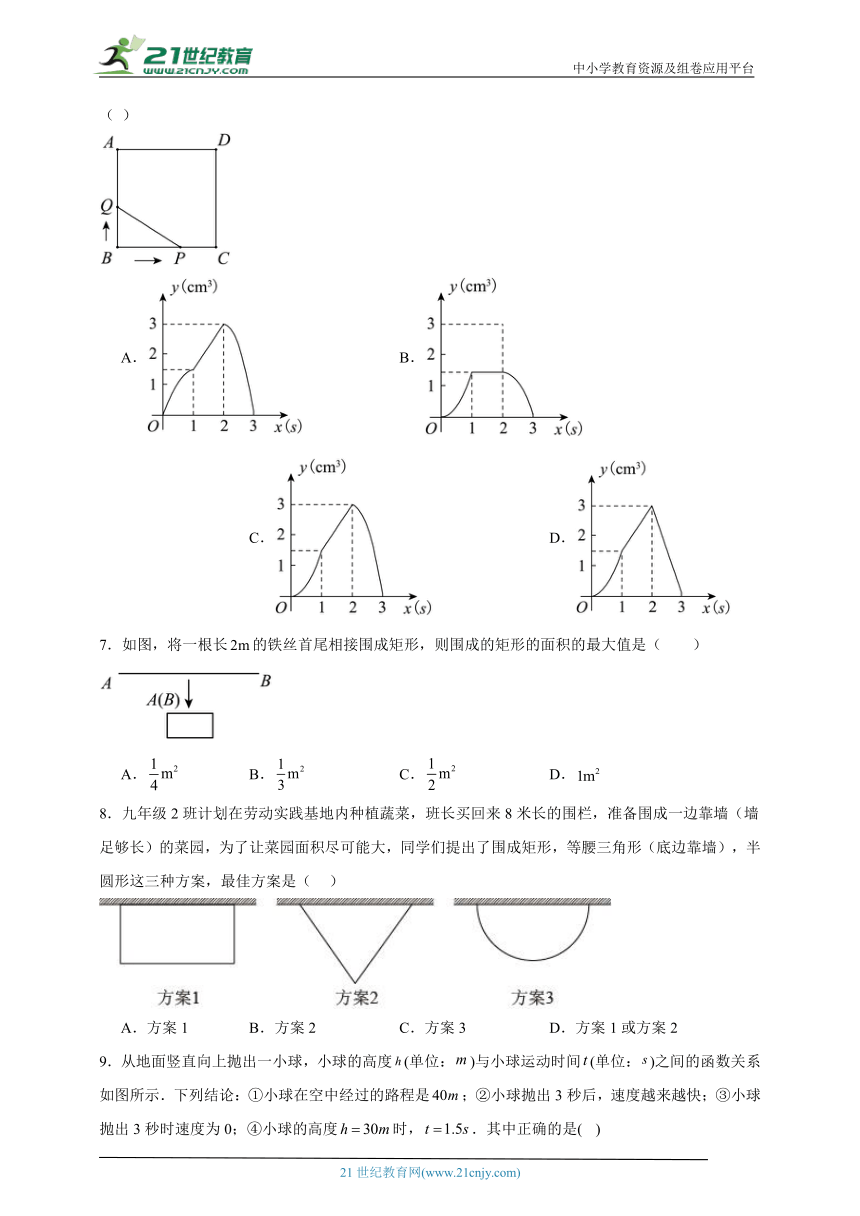
6.如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
A. B. C. D.
7.如图,将一根长的铁丝首尾相接围成矩形,则围成的矩形的面积的最大值是( )
A. B. C. D.
8.九年级2班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形,等腰三角形(底边靠墙),半圆形这三种方案,最佳方案是( )
A.方案1 B.方案2 C.方案3 D.方案1或方案2
9.从地面竖直向上抛出一小球,小球的高度(单位:)与小球运动时间(单位:)之间的函数关系如图所示.下列结论:①小球在空中经过的路程是;②小球抛出3秒后,速度越来越快;③小球抛出3秒时速度为0;④小球的高度时,.其中正确的是( )
A.①④ B.①② C.②③④ D.②③
10.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
A.4米 B.3米 C.2米 D.1米
11.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.则下列结论不正确的是( )
A.小球在空中经过的路程是40m B.小球运动的时间为6s
C.小球抛出3s时,速度为0 D.当s时,小球的高度m
12.一件工艺品进价为100元,标价135元售出,每天可售出100件.根据销售统计,一件工艺品每降价1元出售,则每天可多售出4件,要使每天获得的利润最大,每件需降价的钱数为( )
A.5元 B.10元 C.0元 D.36元
二、填空题
13.如图,已知等腰直角三角形的直角边长与正方形的边长均为,与在同一直线上.点从点出发,以的速度向左运动,运动到点时停止运动,则重叠部分(阴影)的面积与时间之间的函数关系式为 .
14.用一根长为8m的木条,做一个长方形的窗框,若宽为xm,则该窗户的面积y(m2)与x(m)之间的函数关系式为 .
15.某商人将进价为每件元的某种商品按每件元出售,每天可销出件,经试验,把这种商品每件每提价元,每天的销售量就会减少件,则每天所得的利润(元)与售价(元/件)之间的函数关系式为: .
16.一个涵洞成抛物线形,它的截面如图,当水面宽AB=1.6米时,涵洞顶点与水面的距离为2.4m.涵洞所在抛物线的解析式是 .
17.用一块长方形的铁片,把它的四个角各自剪去一个边长是4cm的小方块,然后把四边折起来做成一个没有盖的盒子,已知铁片的长是宽的2倍,则盒子的容积y(cm3)与铁片宽x(cm)的函数关系式为 .
三、解答题
18.某网店专售一款电动牙刷,其成本为20元/支,销售中发现,该商品每天的销售量y(支)与销售单价x(元/支)之间存在如图所示的关系.
(1)请求出y与x的函数关系式;
(2)该款电动牙刷销售单价定为多少元时,每天销售利润最大?最大利润是多少元?
19.用一根长为800cm的木条做一个长方形窗框,若宽为x cm,写出它的面积y与x之间的函数关系式,并判断y是x的二次函数吗?
20.如图,在平面直角坐标系中,二次函数的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为,与y轴交于点,点P是直线下方的抛物线上一动点.
(1)求这个二次函数的表达式;
(2)求出四边形的面积最大时的P点坐标和四边形的最大面积.
21.某农场拟建三间长方形种牛饲养室,饲养室的一面靠墙(墙长50m),中间用两道墙隔开(如图).已知计划中的建筑材料可建墙的总长度为48m,则这三间长方形种牛饲养室的总占地面积的最大值为多少m2?
22.工艺品厂计划生产某种工艺品,每日最高产量是40个,且每日生产的产品全部售出.已知生产x个工艺品成本为P(元),售价为每个R(元),且P与x,R与x的关系式分别为P=500+30x,R=170-2x.
(1)当日产量为多少时,每日获得利润为1950元?
(2)要想获得最大利润,每天必须生产多少个工艺品?
23.在平面直角坐标系中,已知抛物线F:经过点,与y轴交于点.
(1)求抛物线的函数表达式;
(2)在直线上方抛物线上有一动点C,连接交于点D,求的最大值及此时点C的坐标.
24.如图,已知Rt△ABC中,∠A=30°,AC=6.边长为4的等边△DEF沿射线AC运动(A、D、E、C四点共线).当等边△DEF的边DF、EF与Rt△ABC的边AB分别相交于点M、N(M、N不与A、B重合)时,设AD=x.
(1)则△FMN的形状是_______,△ADM的形状是_______;
(2)△ABC与△DEF重叠部分的面积为y,求y关于x的函数解析式,并写出的取值范围;
(3)若以点M为圆心,MN为半径的圆与边AC、EF同时相切,求此时MN的长.
《30.4二次函数的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C B A C C A C D A
题号 11 12
答案 A A
1.A
【分析】根据增长率问题,一般“增长后的量增长前的量(1+增长率)”找出等量关系列方程即可
【详解】第二个月的增长率是,第三个月的增长率是第二个月的两倍,
第三个月的增长率为
第一个月投放辆单车,
第二个月投放辆
第三个月投放量
故选:A.
【点睛】本题考查了根据实际问题列二次函数关系式,解题关键是熟练掌握增长率问题的求解,即“增长后的量增长前的量(1+增长率)”.
2.C
【分析】先根据题意列出二次函数关系式,再根据求二次函数最值的方法求解即可.
【详解】解:由题意可得函数式y=(6-x)x,
即y=x(6-x)=-x2+6x,
当x=-==3时,y有最大值.
当x=3元时,一天出售该种文具盒的总利润y最大.
故选:C.
【点睛】:本题考查了二次函数的性质在实际生活中的应用.最大销售利润的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.
3.B
【分析】本题考查了自变量的取值范围,读懂题意是解题关键.
根据矩形的边长大于0,列出两个不等式,解不等式即可.
【详解】由题意得,
解得.
选B.
4.A
【详解】解:把h(m)与飞行时间t(s)的关系式化成顶点式为:,
∴当t=6时,炮弹到达它的最高点,最高点的高度是91m.
故选A.
5.C
【分析】先求解的长度,再利用三角形的面积公式列二次函数关系式即可.
【详解】解: AB=AD,△ABD的周长为20cm,设
故选:C
【点睛】本题考查的是二次函数的几何应用,列二次函数关系式,掌握“利用图形面积公式列二次函数关系式”是解题的关键.
6.C
【详解】解:由题意可得BQ=x.
①0≤x≤1时,P点在BC边上,BP=3x,
则△BPQ的面积=BP BQ,
可得y= 3x x=;
故A选项错误;
②1<x≤2时,P点在CD边上,
则△BPQ的面积=BQ BC,
可得y= x 3=;
故B选项错误;
③2<x≤3时,P点在AD边上,AP=9﹣3x,
则△BPQ的面积=AP BQ,
可得y= (9﹣3x) x=;
故D选项错误.
故选:C.
7.A
【分析】设围成的矩形的一边长为,围成的矩形面积为,根据矩形面积公式可得S与x 的关系式,再根据二次函数的性质解答即可.
【详解】解:设围成的矩形的一边长为,围成的矩形面积为,则另一边长为,根据题意,得:
,
∴当时,.
故选:A.
【点睛】本题考查了二次函数的应用,属于常考题型,正确列出函数关系式、熟练掌握二次函数的性质是解题的关键.
8.C
【分析】分别计算出三个方案的菜园面积进行比较即可.
【详解】解:方案1,设米,则米,
则菜园的面积
当时,此时散架的最大面积为8平方米;
方案2,当∠时,菜园最大面积平方米;
方案3,半圆的半径
此时菜园最大面积平方米>8平方米,
故选:C
【点睛】本题主要考查了同周长的几何图形的面积的问题,根据周长为8米计算三个方案的边长及半径是解本题的关键.
9.D
【分析】根据函数的图象中的信息判断即可.
【详解】①由图象知小球在空中达到的最大高度是;故①错误;
②小球抛出3秒后,速度越来越快;故②正确;
③小球抛出3秒时达到最高点即速度为0;故③正确;
④设函数解析式为:,
把代入得,解得,
∴函数解析式为,
把代入解析式得,,
解得:或,
∴小球的高度时,或,故④错误;
故选D.
【点睛】本题考查了二次函数的应用,解此题的关键是正确的理解题意
10.A
【详解】)∵y=-x2+4x=,
∴当x=2时,y有最大值4,
∴最大高度为4m.
故选A.
11.A
【分析】选项A、B、C可直接由函数图象中的信息分析得出答案;选项D可由待定系数法求得函数解析式,再将t=1.5s代入计算,即可作出判断.
【详解】解:A、由图象可知,小球在空中达到的最大高度为40m,则小球在空中经过的路程一定大于40m,故选项A错误;
B、由图象可知,小球6s时落地,故小球运动的时间为6s,故选项B正确;
C、小球抛出3秒时达到最高点,即速度为0,故选项C正确;
D、设函数解析式为,将(0,0)代入得:
,
解得,
∴函数解析式为,
∴当t=1.5s时,,
∴选项D正确.
故选:A.
【点睛】本题考查了二次函数在物体运动中的应用,会用待定系数法求函数解析式并数形结合进行分析是解题的关键.
12.A
【详解】设每件需降价的钱数为x元,每天获利y元,
则y=(135﹣x﹣100)(100+4x),即:y=﹣4(x﹣5)2+3600,
由﹣4<0,可得当x=5元时,每天获得的利润最大.
故选A.
【点睛】考点:二次函数的应用
13.
【分析】根据△ABC是等腰直角三角形,则重叠部分也是等腰直角三角形,根据三角形的面积公式即可求解.
【详解】解:∵是等腰直角三角形,
,
∴重叠部分也是等腰直角三角形,
又∵,
∴,
∴,
∴.
故答案为:
【点睛】本题考查了根据实际问题抽象二次函数解析式的知识,根据题意,找到所求量的等量关系是解决问题的关键.
14.y=-x2+4x
【详解】试题分析:由题意8m为长方形的周长,即可表示出长方形的长,再根据长方形的面积公式求解即可.
由题意得函数关系式为.
考点:根据实际问题列函数关系式
点评:解题的关键是读懂题意,找到等量关系,正确列出函数关系式.
15.
【分析】每天所得的利润=(售价-进价)×(原来的销售量-多于10元的售价×10),把相关数值代入化简即可.
【详解】解:每件可获得的利润为(x-8)元,可售出的数量为100-(x-10)×10=200-10x,
∴y=(x-8)×(200-10x)=-10x2+280x-1600,
故答案为y=-10x2+280x-1600.
【点睛】考查列二次函数关系式;得到利润的等量关系是解决本题的关键;得到销售量是解决本题的难点.
16.
【解析】略
17.y=8x2﹣96x+256(x>8)
【详解】试题解析:盒子的长为2x-2×4=2x-8,宽为x-2×4=x-8.
则容积:y=8x2-96x+256(x>8).
故答案为y=8x2-96x+256(x>8).
18.(1)
(2)该款电动牙刷销售单价定为30元时,每天销售利润最大,最大销售利润为1000 元
【分析】(1)设 y与x的函数关系式为,将图中坐标代入,利用待定系数法求解;
(2)设该款电动牙刷每天的销售利润为w元,根据“销售利润单件利润销量”列出销售利润w关于销售单价x的关系式,求出w的最值即可.
【详解】(1)解:设 y与x的函数关系式为,
将,代入,
得,
解得,
y与x的函数关系式为;
(2)解:设该款电动牙刷每天的销售利润为w元,
由题意得
,
当时,w有最大值,w最大值为1000.
答:该款电动牙刷销售单价定为30元时,每天销售利润最大,最大销售利润为1000元.
【点睛】本题考查待定系数法求一次函数解析式,以及二次函数的实际应用,解题的关键是根据“销售利润单件利润销量”列出销售利润w关于销售单价x的关系式.
19.y是x的二次函数
【分析】根据矩形的周长表示出长,根据面积=长×宽即可得出y与x之间的函数关系式.
【详解】解:设宽为xcm,
由题意得,矩形的周长为800cm,
∴矩形的长为cm,
∴y=x×=﹣x2+400x(0<x<400).
y是x的二次函数.
【点睛】本题考查了根据实际问题抽象二次函数解析式及二次函数的定义,属于基础题,表示出矩形的长是解答本题的关键.
20.(1)
(2)点的坐标为:,四边形的面积的最大值为
【分析】本题主要考查了求二次函数解析式,二次函数综合,求一次函数解析式:
(1)将、的坐标代入抛物线的解析式中即可求得待定系数的值;
(2)由于的面积为定值,当四边形的面积最大时,的面积最大;过作y轴的平行线,交直线于,交轴于,求得直线的解析式,可设出点的横坐标,然后根据抛物线和直线的解析式求出、的纵坐标,即可得到的长,以为底,点横坐标的绝对值为高即可求得的面积,由此可得到关于四边形的面积与点横坐标的函数关系式,根据函数的性质即可求出四边形的最大面积及对应的点坐标.
【详解】(1)解:将、两点的坐标代入二次函数解析式得,,
解得:,
∴二次函数的表达式为:;
(2)解:如图,过点作轴的平行线与交于点,与交于点,
设直线的解析式为:,
∴,
解得:,
∴直线的解析式为:,
设,则点的坐标为;
在中,当时,
解得:,,
∴,
∵,
∴,
∴
,
∵,
∴当时,四边形的面积最大,
此时点的坐标为:,四边形的面积的最大值为.
21.这三间长方形种牛饲养室的总占地面积的最大值为.
【分析】要求这三间长方形种牛饲养室的总占地面积的最大值,可设总占地面积为,中间墙长为,根据题目所给出的条件列出与的关系式,再根据函数的性质求出的最大值.
【详解】解:如图所示:
设总占地面积为,的长度为,
由题意知:,
,
,,
,
,
,
当时,可取得最大值,最大值为144.
答:这三间长方形种牛饲养室的总占地面积的最大值为.
【点睛】本题考查实际问题与二次函数最值,解题的关键是需要根据题目列出函数关系式,然后利用函数的性质求出该问题的最值.
22.(1)35;(2)35.
【分析】①通过理解题意,找出题目中所给的等量关系,再根据这一等量关系列出表示利润的函数解析式,并把1950代入求解.
②根据二次函数最值的求法,求得最值.
【详解】(1)根据题意可得
(170-2x)x-(500+30x)=1950.
解得x=35.
(2)设每天所获利润为W.
W=(170-2x)x-(500+30x)
=-2x2+140x-500
=-2(x2-70x)-500
=-2(x2-70x+352-352)-500
=-2(x2-35)2+1950.
当x=35时,W有最大值1950元.
【点睛】本题考查了二次函数的应用,解题的关键是熟悉的运用二次函数的知识点.
23.(1)
(2),
【分析】本题主要考查二次函数的图象与性质,平行线的性质,相似三角形的判定与性质:
(1)用待定系数法求函数解析式即可;
(2)过点C作x轴的垂线交于点M,交x轴于点H,则轴,可知,由此可得,设,且,则,所以,当时,有最大值,即可求出点C的坐标.
【详解】(1)解:将,代入,
得
解得
∴抛物线的函数表达式为;
(2)解:如图,过点C作x轴的垂线交于点M,交x轴于点H,则轴,
∴,
∴,
设直线的表达式为,
把,代入表达式得,
解得
∴直线的表达式为.
设,且,则,
∴,
∵,
∴当时,有最大值,
∴的最大值为,此时点C的坐标为.
24.(1)直角三角形;等腰三角形;(2)当0【详解】(1)直角三角形、等腰三角形
如图1,∵△DEF是等边三角形,
∴∠FDE=∠F=60°
∵∠A=30°,
∴∠AMD=∠FDE-∠A=30°,
∴∠FMN=∠AMD=30°,
∴∠MNF=90°,
即△FMN是直角三角形;
∵∠FDE=60°,
∴∠AMD=∠FDE-∠A=30°,
∴∠AMD=∠A
∴DM=DA,
∴△ADM是等腰三角形;
(2)如图2,∵△ADM是等腰三角形,
∴DM=AD=x,FM=4-x.
又∵∠FED=60°,∠A=30°,
∴∠FNM=90°
∴MN=MF·sinF= ,
FN=MF=(4-x)
∴
当0当2≤x<6时,
CD=6-x
∵∠BCE=90°,∠PEA=60°,
∴PC=
∴
(3)过点M作MG⊥AC于点G,由(2)得DM=x
∵∠MDG=60°,
∴MG=
∵∠MNF=90°,∠MFN=60°,
∴MN=
要使以点M为圆心,MN长为半径的圆与边AC、EF相切,则有MG=MN,
即:=
解得x=2,
圆的半径MN=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
30.4二次函数的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.共享单车为市民出行带来了方便,某单车公司第一个月投放辆单车,计划第三个月投放单车辆,若第二个月的增长率是,第三个月的增长率是第二个月的两倍,那么与的函数关系是 ( )
A. B.
C. D.
2.出售某种文具盒,若每个可获利x元,一天可售出(6-x)个.当一天出售该种文具盒的总利润y最大时,x的值为( )
A.1 B.2 C.3 D.4
3.已知x为矩形的一边长,其面积为y,且, 则自变量的取值范围是( )
A. B. C.0≤x≤4 D.
4.烟花厂为热烈庆祝“十一国庆”,特别设计制作一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是,礼炮点火升空后会在最高点处引爆,则这种礼炮能上升的最大高度为( )
A.91米 B.90米 C.81米 D.80米
5.如图,四边形ABCD中,AB=AD,CE⊥BD,CE=BD.若△ABD的周长为20cm,则△BCD的面积S(cm2)与AB的长(cm)之间的函数关系式可以是( )
A. B.
C. D.
6.如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
A. B. C. D.
7.如图,将一根长的铁丝首尾相接围成矩形,则围成的矩形的面积的最大值是( )
A. B. C. D.
8.九年级2班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形,等腰三角形(底边靠墙),半圆形这三种方案,最佳方案是( )
A.方案1 B.方案2 C.方案3 D.方案1或方案2
9.从地面竖直向上抛出一小球,小球的高度(单位:)与小球运动时间(单位:)之间的函数关系如图所示.下列结论:①小球在空中经过的路程是;②小球抛出3秒后,速度越来越快;③小球抛出3秒时速度为0;④小球的高度时,.其中正确的是( )
A.①④ B.①② C.②③④ D.②③
10.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
A.4米 B.3米 C.2米 D.1米
11.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.则下列结论不正确的是( )
A.小球在空中经过的路程是40m B.小球运动的时间为6s
C.小球抛出3s时,速度为0 D.当s时,小球的高度m
12.一件工艺品进价为100元,标价135元售出,每天可售出100件.根据销售统计,一件工艺品每降价1元出售,则每天可多售出4件,要使每天获得的利润最大,每件需降价的钱数为( )
A.5元 B.10元 C.0元 D.36元
二、填空题
13.如图,已知等腰直角三角形的直角边长与正方形的边长均为,与在同一直线上.点从点出发,以的速度向左运动,运动到点时停止运动,则重叠部分(阴影)的面积与时间之间的函数关系式为 .
14.用一根长为8m的木条,做一个长方形的窗框,若宽为xm,则该窗户的面积y(m2)与x(m)之间的函数关系式为 .
15.某商人将进价为每件元的某种商品按每件元出售,每天可销出件,经试验,把这种商品每件每提价元,每天的销售量就会减少件,则每天所得的利润(元)与售价(元/件)之间的函数关系式为: .
16.一个涵洞成抛物线形,它的截面如图,当水面宽AB=1.6米时,涵洞顶点与水面的距离为2.4m.涵洞所在抛物线的解析式是 .
17.用一块长方形的铁片,把它的四个角各自剪去一个边长是4cm的小方块,然后把四边折起来做成一个没有盖的盒子,已知铁片的长是宽的2倍,则盒子的容积y(cm3)与铁片宽x(cm)的函数关系式为 .
三、解答题
18.某网店专售一款电动牙刷,其成本为20元/支,销售中发现,该商品每天的销售量y(支)与销售单价x(元/支)之间存在如图所示的关系.
(1)请求出y与x的函数关系式;
(2)该款电动牙刷销售单价定为多少元时,每天销售利润最大?最大利润是多少元?
19.用一根长为800cm的木条做一个长方形窗框,若宽为x cm,写出它的面积y与x之间的函数关系式,并判断y是x的二次函数吗?
20.如图,在平面直角坐标系中,二次函数的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为,与y轴交于点,点P是直线下方的抛物线上一动点.
(1)求这个二次函数的表达式;
(2)求出四边形的面积最大时的P点坐标和四边形的最大面积.
21.某农场拟建三间长方形种牛饲养室,饲养室的一面靠墙(墙长50m),中间用两道墙隔开(如图).已知计划中的建筑材料可建墙的总长度为48m,则这三间长方形种牛饲养室的总占地面积的最大值为多少m2?
22.工艺品厂计划生产某种工艺品,每日最高产量是40个,且每日生产的产品全部售出.已知生产x个工艺品成本为P(元),售价为每个R(元),且P与x,R与x的关系式分别为P=500+30x,R=170-2x.
(1)当日产量为多少时,每日获得利润为1950元?
(2)要想获得最大利润,每天必须生产多少个工艺品?
23.在平面直角坐标系中,已知抛物线F:经过点,与y轴交于点.
(1)求抛物线的函数表达式;
(2)在直线上方抛物线上有一动点C,连接交于点D,求的最大值及此时点C的坐标.
24.如图,已知Rt△ABC中,∠A=30°,AC=6.边长为4的等边△DEF沿射线AC运动(A、D、E、C四点共线).当等边△DEF的边DF、EF与Rt△ABC的边AB分别相交于点M、N(M、N不与A、B重合)时,设AD=x.
(1)则△FMN的形状是_______,△ADM的形状是_______;
(2)△ABC与△DEF重叠部分的面积为y,求y关于x的函数解析式,并写出的取值范围;
(3)若以点M为圆心,MN为半径的圆与边AC、EF同时相切,求此时MN的长.
《30.4二次函数的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C B A C C A C D A
题号 11 12
答案 A A
1.A
【分析】根据增长率问题,一般“增长后的量增长前的量(1+增长率)”找出等量关系列方程即可
【详解】第二个月的增长率是,第三个月的增长率是第二个月的两倍,
第三个月的增长率为
第一个月投放辆单车,
第二个月投放辆
第三个月投放量
故选:A.
【点睛】本题考查了根据实际问题列二次函数关系式,解题关键是熟练掌握增长率问题的求解,即“增长后的量增长前的量(1+增长率)”.
2.C
【分析】先根据题意列出二次函数关系式,再根据求二次函数最值的方法求解即可.
【详解】解:由题意可得函数式y=(6-x)x,
即y=x(6-x)=-x2+6x,
当x=-==3时,y有最大值.
当x=3元时,一天出售该种文具盒的总利润y最大.
故选:C.
【点睛】:本题考查了二次函数的性质在实际生活中的应用.最大销售利润的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.
3.B
【分析】本题考查了自变量的取值范围,读懂题意是解题关键.
根据矩形的边长大于0,列出两个不等式,解不等式即可.
【详解】由题意得,
解得.
选B.
4.A
【详解】解:把h(m)与飞行时间t(s)的关系式化成顶点式为:,
∴当t=6时,炮弹到达它的最高点,最高点的高度是91m.
故选A.
5.C
【分析】先求解的长度,再利用三角形的面积公式列二次函数关系式即可.
【详解】解: AB=AD,△ABD的周长为20cm,设
故选:C
【点睛】本题考查的是二次函数的几何应用,列二次函数关系式,掌握“利用图形面积公式列二次函数关系式”是解题的关键.
6.C
【详解】解:由题意可得BQ=x.
①0≤x≤1时,P点在BC边上,BP=3x,
则△BPQ的面积=BP BQ,
可得y= 3x x=;
故A选项错误;
②1<x≤2时,P点在CD边上,
则△BPQ的面积=BQ BC,
可得y= x 3=;
故B选项错误;
③2<x≤3时,P点在AD边上,AP=9﹣3x,
则△BPQ的面积=AP BQ,
可得y= (9﹣3x) x=;
故D选项错误.
故选:C.
7.A
【分析】设围成的矩形的一边长为,围成的矩形面积为,根据矩形面积公式可得S与x 的关系式,再根据二次函数的性质解答即可.
【详解】解:设围成的矩形的一边长为,围成的矩形面积为,则另一边长为,根据题意,得:
,
∴当时,.
故选:A.
【点睛】本题考查了二次函数的应用,属于常考题型,正确列出函数关系式、熟练掌握二次函数的性质是解题的关键.
8.C
【分析】分别计算出三个方案的菜园面积进行比较即可.
【详解】解:方案1,设米,则米,
则菜园的面积
当时,此时散架的最大面积为8平方米;
方案2,当∠时,菜园最大面积平方米;
方案3,半圆的半径
此时菜园最大面积平方米>8平方米,
故选:C
【点睛】本题主要考查了同周长的几何图形的面积的问题,根据周长为8米计算三个方案的边长及半径是解本题的关键.
9.D
【分析】根据函数的图象中的信息判断即可.
【详解】①由图象知小球在空中达到的最大高度是;故①错误;
②小球抛出3秒后,速度越来越快;故②正确;
③小球抛出3秒时达到最高点即速度为0;故③正确;
④设函数解析式为:,
把代入得,解得,
∴函数解析式为,
把代入解析式得,,
解得:或,
∴小球的高度时,或,故④错误;
故选D.
【点睛】本题考查了二次函数的应用,解此题的关键是正确的理解题意
10.A
【详解】)∵y=-x2+4x=,
∴当x=2时,y有最大值4,
∴最大高度为4m.
故选A.
11.A
【分析】选项A、B、C可直接由函数图象中的信息分析得出答案;选项D可由待定系数法求得函数解析式,再将t=1.5s代入计算,即可作出判断.
【详解】解:A、由图象可知,小球在空中达到的最大高度为40m,则小球在空中经过的路程一定大于40m,故选项A错误;
B、由图象可知,小球6s时落地,故小球运动的时间为6s,故选项B正确;
C、小球抛出3秒时达到最高点,即速度为0,故选项C正确;
D、设函数解析式为,将(0,0)代入得:
,
解得,
∴函数解析式为,
∴当t=1.5s时,,
∴选项D正确.
故选:A.
【点睛】本题考查了二次函数在物体运动中的应用,会用待定系数法求函数解析式并数形结合进行分析是解题的关键.
12.A
【详解】设每件需降价的钱数为x元,每天获利y元,
则y=(135﹣x﹣100)(100+4x),即:y=﹣4(x﹣5)2+3600,
由﹣4<0,可得当x=5元时,每天获得的利润最大.
故选A.
【点睛】考点:二次函数的应用
13.
【分析】根据△ABC是等腰直角三角形,则重叠部分也是等腰直角三角形,根据三角形的面积公式即可求解.
【详解】解:∵是等腰直角三角形,
,
∴重叠部分也是等腰直角三角形,
又∵,
∴,
∴,
∴.
故答案为:
【点睛】本题考查了根据实际问题抽象二次函数解析式的知识,根据题意,找到所求量的等量关系是解决问题的关键.
14.y=-x2+4x
【详解】试题分析:由题意8m为长方形的周长,即可表示出长方形的长,再根据长方形的面积公式求解即可.
由题意得函数关系式为.
考点:根据实际问题列函数关系式
点评:解题的关键是读懂题意,找到等量关系,正确列出函数关系式.
15.
【分析】每天所得的利润=(售价-进价)×(原来的销售量-多于10元的售价×10),把相关数值代入化简即可.
【详解】解:每件可获得的利润为(x-8)元,可售出的数量为100-(x-10)×10=200-10x,
∴y=(x-8)×(200-10x)=-10x2+280x-1600,
故答案为y=-10x2+280x-1600.
【点睛】考查列二次函数关系式;得到利润的等量关系是解决本题的关键;得到销售量是解决本题的难点.
16.
【解析】略
17.y=8x2﹣96x+256(x>8)
【详解】试题解析:盒子的长为2x-2×4=2x-8,宽为x-2×4=x-8.
则容积:y=8x2-96x+256(x>8).
故答案为y=8x2-96x+256(x>8).
18.(1)
(2)该款电动牙刷销售单价定为30元时,每天销售利润最大,最大销售利润为1000 元
【分析】(1)设 y与x的函数关系式为,将图中坐标代入,利用待定系数法求解;
(2)设该款电动牙刷每天的销售利润为w元,根据“销售利润单件利润销量”列出销售利润w关于销售单价x的关系式,求出w的最值即可.
【详解】(1)解:设 y与x的函数关系式为,
将,代入,
得,
解得,
y与x的函数关系式为;
(2)解:设该款电动牙刷每天的销售利润为w元,
由题意得
,
当时,w有最大值,w最大值为1000.
答:该款电动牙刷销售单价定为30元时,每天销售利润最大,最大销售利润为1000元.
【点睛】本题考查待定系数法求一次函数解析式,以及二次函数的实际应用,解题的关键是根据“销售利润单件利润销量”列出销售利润w关于销售单价x的关系式.
19.y是x的二次函数
【分析】根据矩形的周长表示出长,根据面积=长×宽即可得出y与x之间的函数关系式.
【详解】解:设宽为xcm,
由题意得,矩形的周长为800cm,
∴矩形的长为cm,
∴y=x×=﹣x2+400x(0<x<400).
y是x的二次函数.
【点睛】本题考查了根据实际问题抽象二次函数解析式及二次函数的定义,属于基础题,表示出矩形的长是解答本题的关键.
20.(1)
(2)点的坐标为:,四边形的面积的最大值为
【分析】本题主要考查了求二次函数解析式,二次函数综合,求一次函数解析式:
(1)将、的坐标代入抛物线的解析式中即可求得待定系数的值;
(2)由于的面积为定值,当四边形的面积最大时,的面积最大;过作y轴的平行线,交直线于,交轴于,求得直线的解析式,可设出点的横坐标,然后根据抛物线和直线的解析式求出、的纵坐标,即可得到的长,以为底,点横坐标的绝对值为高即可求得的面积,由此可得到关于四边形的面积与点横坐标的函数关系式,根据函数的性质即可求出四边形的最大面积及对应的点坐标.
【详解】(1)解:将、两点的坐标代入二次函数解析式得,,
解得:,
∴二次函数的表达式为:;
(2)解:如图,过点作轴的平行线与交于点,与交于点,
设直线的解析式为:,
∴,
解得:,
∴直线的解析式为:,
设,则点的坐标为;
在中,当时,
解得:,,
∴,
∵,
∴,
∴
,
∵,
∴当时,四边形的面积最大,
此时点的坐标为:,四边形的面积的最大值为.
21.这三间长方形种牛饲养室的总占地面积的最大值为.
【分析】要求这三间长方形种牛饲养室的总占地面积的最大值,可设总占地面积为,中间墙长为,根据题目所给出的条件列出与的关系式,再根据函数的性质求出的最大值.
【详解】解:如图所示:
设总占地面积为,的长度为,
由题意知:,
,
,,
,
,
,
当时,可取得最大值,最大值为144.
答:这三间长方形种牛饲养室的总占地面积的最大值为.
【点睛】本题考查实际问题与二次函数最值,解题的关键是需要根据题目列出函数关系式,然后利用函数的性质求出该问题的最值.
22.(1)35;(2)35.
【分析】①通过理解题意,找出题目中所给的等量关系,再根据这一等量关系列出表示利润的函数解析式,并把1950代入求解.
②根据二次函数最值的求法,求得最值.
【详解】(1)根据题意可得
(170-2x)x-(500+30x)=1950.
解得x=35.
(2)设每天所获利润为W.
W=(170-2x)x-(500+30x)
=-2x2+140x-500
=-2(x2-70x)-500
=-2(x2-70x+352-352)-500
=-2(x2-35)2+1950.
当x=35时,W有最大值1950元.
【点睛】本题考查了二次函数的应用,解题的关键是熟悉的运用二次函数的知识点.
23.(1)
(2),
【分析】本题主要考查二次函数的图象与性质,平行线的性质,相似三角形的判定与性质:
(1)用待定系数法求函数解析式即可;
(2)过点C作x轴的垂线交于点M,交x轴于点H,则轴,可知,由此可得,设,且,则,所以,当时,有最大值,即可求出点C的坐标.
【详解】(1)解:将,代入,
得
解得
∴抛物线的函数表达式为;
(2)解:如图,过点C作x轴的垂线交于点M,交x轴于点H,则轴,
∴,
∴,
设直线的表达式为,
把,代入表达式得,
解得
∴直线的表达式为.
设,且,则,
∴,
∵,
∴当时,有最大值,
∴的最大值为,此时点C的坐标为.
24.(1)直角三角形;等腰三角形;(2)当0
如图1,∵△DEF是等边三角形,
∴∠FDE=∠F=60°
∵∠A=30°,
∴∠AMD=∠FDE-∠A=30°,
∴∠FMN=∠AMD=30°,
∴∠MNF=90°,
即△FMN是直角三角形;
∵∠FDE=60°,
∴∠AMD=∠FDE-∠A=30°,
∴∠AMD=∠A
∴DM=DA,
∴△ADM是等腰三角形;
(2)如图2,∵△ADM是等腰三角形,
∴DM=AD=x,FM=4-x.
又∵∠FED=60°,∠A=30°,
∴∠FNM=90°
∴MN=MF·sinF= ,
FN=MF=(4-x)
∴
当0
CD=6-x
∵∠BCE=90°,∠PEA=60°,
∴PC=
∴
(3)过点M作MG⊥AC于点G,由(2)得DM=x
∵∠MDG=60°,
∴MG=
∵∠MNF=90°,∠MFN=60°,
∴MN=
要使以点M为圆心,MN长为半径的圆与边AC、EF相切,则有MG=MN,
即:=
解得x=2,
圆的半径MN=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
