31.2 随机事件的概率 同步练习(含解析)
文档属性
| 名称 | 31.2 随机事件的概率 同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 590.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-02 05:44:32 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
31.2随机事件的概率
学校:___________姓名:___________班级:___________考号:___________
一、单选题
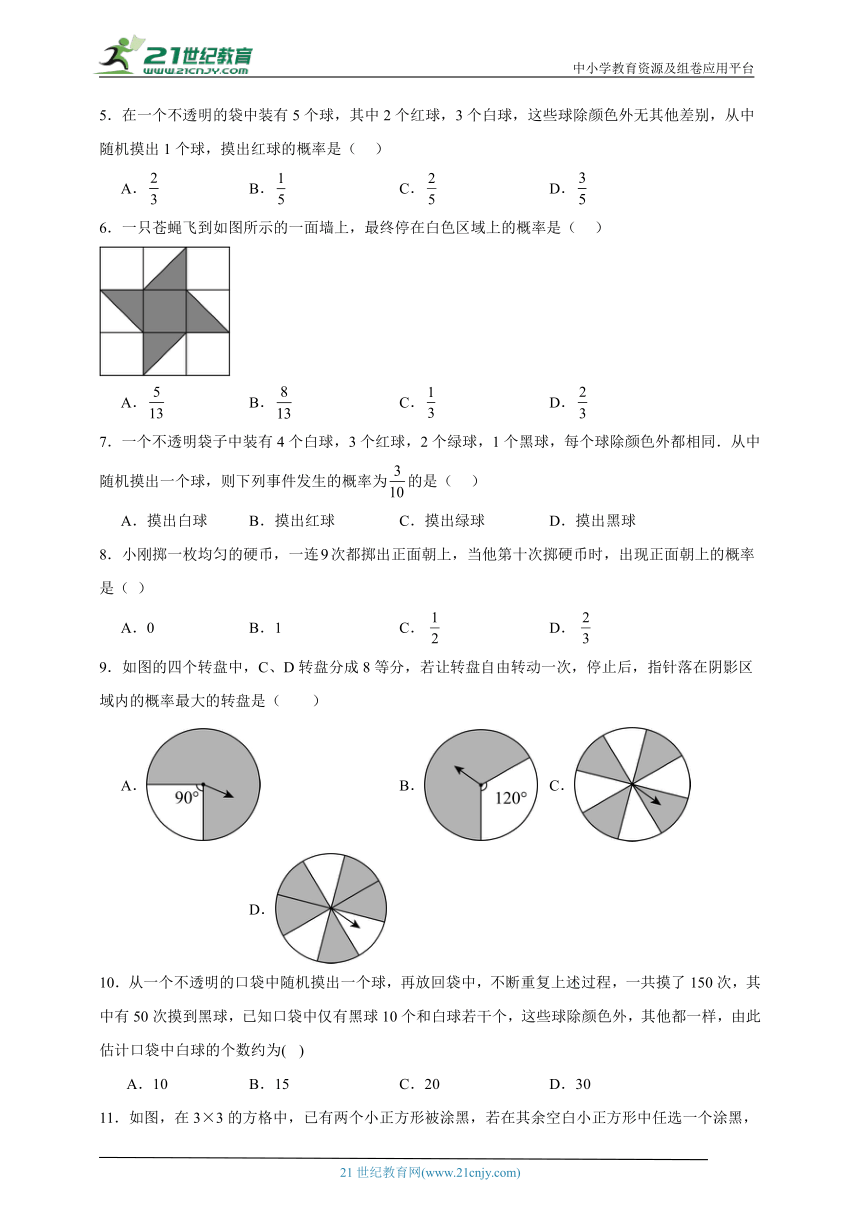
1.七巧板是一种传统智力玩具,可以由七块板组成一个大正方形,其中七块板分别是五块等腰直角三角形、一块正方形和一块平行四边形.如图是七巧板的一种拼图图案,将一个飞镖随机投掷到大正方形上,则飞镖落在三角形区域的概率为( )
A. B. C. D.
2.如图,从一个大正方形中截去面积为和的两个小正方形,若随机向大正方形内投一粒米,则米粒落在图中阴影部分的概率为( )
A. B. C. D.
3.平行四边形ABCD的对角线AC、BD相交于O,给出的四个条件①AB=BC;②∠ABC=90°;③OA=OB;④AC⊥BD,从所给的四个条件中任选两个,能判定平行四边形ABCD是正方形的概率是( )
A. B. C. D.
4.一个选择题有四个选项,其中只有一个是正确的,随机选一个,选择正确的概率是( )
A.0 B. C. D.1
5.在一个不透明的袋中装有5个球,其中2个红球,3个白球,这些球除颜色外无其他差别,从中随机摸出1个球,摸出红球的概率是( )
A. B. C. D.
6.一只苍蝇飞到如图所示的一面墙上,最终停在白色区域上的概率是( )
A. B. C. D.
7.一个不透明袋子中装有4个白球,3个红球,2个绿球,1个黑球,每个球除颜色外都相同.从中随机摸出一个球,则下列事件发生的概率为的是( )
A.摸出白球 B.摸出红球 C.摸出绿球 D.摸出黑球
8.小刚掷一枚均匀的硬币,一连次都掷出正面朝上,当他第十次掷硬币时,出现正面朝上的概率是( )
A.0 B.1 C. D.
9.如图的四个转盘中,C、D转盘分成8等分,若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是( )
A. B. C. D.
10.从一个不透明的口袋中随机摸出一个球,再放回袋中,不断重复上述过程,一共摸了150次,其中有50次摸到黑球,已知口袋中仅有黑球10个和白球若干个,这些球除颜色外,其他都一样,由此估计口袋中白球的个数约为( )
A.10 B.15 C.20 D.30
11.如图,在3×3的方格中,已有两个小正方形被涂黑,若在其余空白小正方形中任选一个涂黑,则所得图案是一个轴对称图形的概率是( )
A. B. C. D.
12.李老师准备在班内开展“道德”“心理”“安全”三场专题教育讲座,若三场讲座随机安排,则“心理”专题讲座被安排在第一场的概率为( )
A. B. C. D.
二、填空题
13.如图,转盘中6个小扇形的面积都相等,任意转动转盘1次,当转盘停止转动时,指针指向红色区域的概率为 .
14.在相同的条件下,随机抛掷一枚质地均匀的硬币10次,有7次正面向上.当抛掷第11次时,正面向上的概率为 .
15.小明和小丽按如下规则做游戏:桌面上放有7根火柴棒,每次取1根或2根,最后取完者获胜.若由小明先取,且小明获胜是必然事件,则小明第一次应该取走火柴棒的根数是 .
16.在用模拟试验估计40名同学中有两个同学是同一天生日的概率中,将小球每次搅匀的目的是 .
17.一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上,每块地砖的大小、质地完全相同,则该小球停留在阴影部分的概率是 .
三、解答题
18.已知地球表面陆地面积与海洋面积的比约为.如果宇宙中飞来一块陨石落在地球上,“落在陆地上”与“落在海洋里”哪种可能性大?
19.自五月中旬开始,教育局开始组织县域内各校八年级学生进行生物实验加试,某校把参加加试的学生分成5个组,以抽签方式决定各组加试顺序,工作人员准备背面完全一样的5张纸牌,在纸牌的另一面分别写上1,2,3,4,5,将纸牌洗均后背面朝上,由每个组的带队老师随机抽取一张纸牌,请思考以下问题:
(1)抽到的数字有几种可能的结果?
(2)抽到纸牌数字是1的概率是多少?
(3)抽到纸牌数字大于3的概率是多少?
20.不透明袋子中装有5个红球、3个绿球,这些球除了颜色外无其他差别.从袋子中随机摸出1个球,“摸出红球”和“摸出绿球”的可能性相等吗?它们的概率分别为多少?
21.甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
22.有一个转盘如图所示,被分成6个大小相同的扇形,颜色分别为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).有下列事件:①指针指向红色;②指针指向绿色;③指针指向黄色;④指针不指向黄色.
(1)在上述事件中,可能性最大的是________,可能性最小的事件是________(填序号);
(2)将上述事件按发生的可能性从小到大的顺序排列________(填序号).
23.小蒙设计了两个抽奖游戏,游戏一是转盘游戏,如图,转盘被等分成了4个扇形,共有红、黄和蓝三种颜色,自由转动转盘,指针停在红色时会得到奖励;游戏二是摸球游戏,袋子里有2个红球、2个黄球和1个蓝球,每个球除颜色外都相同,任意摸出一个球,摸到红球会得到奖励.小雨要参加抽奖游戏,你建议她参加哪一个游戏?请说明理由.
24.某商场进行有奖促销活动,转盘分为5个扇形区域,分别是特等奖、一等奖、二等奖、三等奖及不获奖,制作转盘时,将获奖扇形区域圆心角分配如下表:
奖次 特等奖 一等奖 二等奖 三等奖
圆心角
如果不用转盘,请设计一种等效实验方案(要求写清楚替代工具和实验规则).
《31.2随机事件的概率》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A D C C D B C A C
题号 11 12
答案 C C
1.A
【分析】设小正方形的边长为1,计算出小正方形的面积为1,平行四边形的面积为1,大正方形的面积为8,由此得三角形区域的面积为8-1-1=6,根据概率公式计算飞镖落在三角形区域的概率即可.
【详解】解:设小正方形的边长为1,则小正方形的面积为1,
平行四边形的底边长为1,高为1,则平行四边形的面积为1,
大正方形的边长为,大正方形的面积为8,
则三角形区域的面积为8-1-1=6,飞镖落在三角形区域的概率为,
故选:A.
【点睛】此题考查了求简单事件的概率,正确理解图形中各小图形的边长的关系及面积的计算方法是解题的关键.
2.A
【分析】求出阴影部分的面积占大正方形的份数即可判断.
【详解】解:∵两个小正方形的面积为和,
∴两个小正方形的边长为和,
∴大正方形的边长为,
∴大正方形的面积为,
∴阴影部分的面积为,
∴米粒落在图中阴影部分的概率为,
故选:A.
【点睛】本题主要考查了几何概率,熟练掌握正方形边长与面积的关系是解题关键.
3.D
【分析】先确定组合的总数,再确定能判定是正方形的组合数,根据概率公式计算即可.
【详解】一共有①②,①③,①④,②③,②④;③④6种组合数,
其中能判定四边形是正方形有①②,①③,②④,③④4种组合数,
所以能判定平行四边形ABCD是正方形的概率是,
故选D.
【点睛】本题考查了概率公式计算,熟练掌握正方形的判定是解题的关键.
4.C
【分析】本题主要考查了简单的概率计算,解题的关键在于能够熟练掌握概率计算公式.
根据一共有4个答案,那么就有4种等可能性的结果,其中只有1个正确答案,那么只有一种是正确的结果,由此利用概率公式计算即可.
【详解】解:∵一共有4个答案,其中只有1个正确答案,
∴选择正确的概率是.
故选C.
5.C
【分析】根据简单事件的概率计算公式即可得.
【详解】解:由题意得:从不透明的袋中随机摸出1个球共有5种等可能性的结果,其中,摸出红球的结果有2种,
则从中随机摸出1个球,摸出红球的概率是,
故选:C.
【点睛】本题考查了求概率,熟练掌握概率公式是解题关键.
6.D
【分析】苍蝇停在白色区域上的概率等于白砖的面积除以整个墙面的面积..
【详解】如图,把墙面上一块砖的面积看成1,墙的面积是9,白砖的面积是6
∴苍蝇停在白色区域上的概率=
故选D
【点睛】本题考查了几何概率,熟练掌握几何概率的计算方法是解题的关键.
7.B
【分析】本题考查了概率,熟练掌握概率公式是解题关键.分别求出摸出四种颜色球的概率,即可得到答案.
【详解】解:A、摸出白球的概率为,不符合题意;
B、摸出红球,符合题意;
C、摸出绿球,不符合题意;
D、摸出黑球,不符合题意;
故选:B.
8.C
【详解】小刚掷一枚硬币,他第十次掷硬币,出现正面朝上还是反而朝上,与前面九次没有任何联系,这十次掷硬币,是十个相互独立的事件,每一次正面朝上与反面朝上,都是概率相同的.故选C.
9.A
【详解】解:A.如图所示:指针落在阴影区域内的概率为:;
B.如图所示:指针落在阴影区域内的概率为:;
C.如图所示:指针落在阴影区域内的概率为:;
D.如图所示:指针落在阴影区域内的概率为:,
∵,
∴指针落在阴影区域内的概率最大的转盘是:.
故选:A.
【点睛】本题考查几何概率.
10.C
【解析】略
11.C
【分析】分别把7个空白处涂黑,判断所得图案是否为轴对称图形,再根据概率公式进行计算.
【详解】在其余空白小正方形中任选一个涂黑,
如上图,把①②③处任意一处涂黑时,图案为轴对称图形,
故所得图案是一个轴对称图形的概率.
故选:C.
【点睛】本题考查了概率公式,轴对称图形.熟记概率公式和能识别轴对称图形是解决此题的关键.
12.C
【分析】利用概率公式求解即可求得答案.
【详解】解: 班内开展“道德”“心理”“安全”三场专题教育讲座,
“心理”专题讲座被安排在第一场的概率.
故选:C.
【点睛】本题主要考查了概率公式的应用,用到的知识点为:概率=所求情况数与总情况数之比,掌握概率公式是解题的关键.
13..
【详解】试题分析:∵圆被等分成6份,其中红色部分占2份,∴落在阴影区域的概率==,故答案为.
考点:几何概率.
14.
【分析】掷一枚质地均匀的硬币,有两种结果,正面或反面朝上,每种结果等可能出现,利用概率公式即可求得答案.
【详解】解:∵掷一枚质地均匀的硬币,有两种结果:正面朝上,反面朝上,每种结果等可能出现,∴她第11次掷这枚硬币时,正面向上的概率是:,
故答案为:.
【点睛】此题考查了概率公式,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.
15.1
【详解】【分析】要保证小明获胜是必然事件,则小明必然要取到第7根火柴,进行倒推,可以发现只要两人所取的根数之和为3就能保证小明获胜.
【详解】如果小明第一次取走1根,剩下了6根,后面无论如取,只要保证每轮两人所取的根数之和为3,就能保证小明将取走最后一根火柴,
而6是3的倍数,因此小明第一次应该取走1根,
故答案为1.
【点睛】本题考查了随机事件,概率的意义,理解题目信息,判断出使两人所取的根数之和是3是解题的关键.
16.使每个球出现的机会均等
【分析】根据概率的等可能性判断即可.
【详解】解:每次模拟试验后将小球每次搅匀是为了使每个球出现的机会均等,
故答案为:使每个球出现的机会均等.
【点睛】本题考查了概率的等可能性,确保等可能性是解题的关键.
17.
【分析】本题考查几何概率模型,用阴影部分的面积除以总面积得到该小球停留在阴影部分的概率即可得到答案.熟记几何概率模型求概率的方法:概率阴影部分面积总面积.
【详解】
解:设图中一个阴影部分三角形的面积为,由图可知它为一个小正方形面积的,
所以所有阴影部分的面积是,大正方形的面积是个小正方形面积,即,
该小球停留在阴影部分的概率是,
故答案为:.
18.“落在海洋里”的可能性更大.
【分析】据几何概率的求法:看海洋的面积占总面积的多少即为所求的概率.
【详解】解:根据题意可得:地球表面陆地面积与海洋面积的比约为3:7,
即相当于将地球总面积分为10份,海洋占7份,
所以落在海洋里的概率是.
所以 “落在海洋里”的可能性更大.
【点睛】本题考查了几何概率的求法,理解题意是解题的关键.首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.
19.(1)有5种结果
(2)
(3)
【分析】本题考查了简单事件的概率,求出所有可能结果数及事件发生的可能结果数,即可求得概率.
(1)根据纸牌数即可确定抽到的可能结果数;
(2)由简单事件概率公式即可求解;
(3)由简单事件概率公式即可求解.
【详解】(1)解:背面朝上且完全一样的5张纸牌随机抽取,有5种结果,且被抽取的可能性是相同的.
(2)解:共有5种结果,每种结果出现的可能性是相同的,
所以抽纸牌1的概率为;
(3)解:有5种等可能结果,大于3的有4和5两种结果,
所以抽纸牌大于3的概率为.
20.“摸出红球”与“摸出绿球”的可能性不相等,它们的概率分别为和.
【分析】根据概率=某种颜色的球的个数÷球的总数进行求解即可.
【详解】解:“摸出红球”与“摸出绿球”的可能性不相等,
它们的概率分别为和.
【点睛】本题主要考查了简单的概率计算,解题的关键在于能够熟练掌握相关知识进行求解.
21.甲班成功的机会大,理由见解析.
【分析】首先分别求出在两个班的160厘米以上的女生中抽出一个作为旗手的概率,然后进行比较,哪个大在哪个班成功的机会大.
【详解】∵已经限定在身高160厘米以上的女生中抽选旗手,甲班身高在160厘米以上的女同学3人,乙班身高在160厘米以上的女同学8人,
∴在甲班被抽到的概率为,在乙甲班被抽到的概率为,
∵>,
∴在甲班被抽到的机会大.
22.(1)④;②
(2)②③①④
【分析】分别求出摸出各种颜色球的概率,即可比较出摸出何种颜色球的可能性大.
【详解】(1)∵共3红2黄1绿相等的六部分,
∴①指针指向红色的概率为;
②指针指向绿色的概率为;
③指针指向黄色的概率为;
④指针不指向黄色为,
∴可能性最大的是④,可能性最小的事件是②,
故答案为:④;②;
(2)由(1)得:②<③<①<④,
故答案为:②③①④.
【点睛】本题考查的是可能性大小的判断,解决这类题目要注意具体情况具体对待.用到的知识点为:可能性等于所求情况数与总情况数之比.
23.参加游戏一
【分析】分别求出两种游戏方案中,获奖的概率,进而比较即可
【详解】游戏一:转盘分为四等分,红色占两份,
∴获奖概率为
游戏二:共有五个球,摸出一个球是红色的概率为
故选择游戏一获奖概率更大.
【点睛】本题考查了概率,熟练掌握等可能事件的概率公式是解题的关键.
24.见解析
【分析】根据扇形圆心角度数可得出各种奖项所占比例,进而利用抽签方式得出等效试验方案.
【详解】解:由题意可得出:
可采取“抓阄”或“抽签”等方法替代,
例如在一个不透明的箱子里放进36个除标号不同外,其他均一样的乒乓球,
其中1个标“特”,2个标“一”,3个标“二”,9个标“三”,其余不标数字,
摸出标有哪个奖次的乒乓球,则获相应的等级的奖品.
【点睛】此题主要考查了模拟实验,替代实验的设计方案很多,但要抓住问题的实质,即各奖项发生的概率要保持不变.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
31.2随机事件的概率
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.七巧板是一种传统智力玩具,可以由七块板组成一个大正方形,其中七块板分别是五块等腰直角三角形、一块正方形和一块平行四边形.如图是七巧板的一种拼图图案,将一个飞镖随机投掷到大正方形上,则飞镖落在三角形区域的概率为( )
A. B. C. D.
2.如图,从一个大正方形中截去面积为和的两个小正方形,若随机向大正方形内投一粒米,则米粒落在图中阴影部分的概率为( )
A. B. C. D.
3.平行四边形ABCD的对角线AC、BD相交于O,给出的四个条件①AB=BC;②∠ABC=90°;③OA=OB;④AC⊥BD,从所给的四个条件中任选两个,能判定平行四边形ABCD是正方形的概率是( )
A. B. C. D.
4.一个选择题有四个选项,其中只有一个是正确的,随机选一个,选择正确的概率是( )
A.0 B. C. D.1
5.在一个不透明的袋中装有5个球,其中2个红球,3个白球,这些球除颜色外无其他差别,从中随机摸出1个球,摸出红球的概率是( )
A. B. C. D.
6.一只苍蝇飞到如图所示的一面墙上,最终停在白色区域上的概率是( )
A. B. C. D.
7.一个不透明袋子中装有4个白球,3个红球,2个绿球,1个黑球,每个球除颜色外都相同.从中随机摸出一个球,则下列事件发生的概率为的是( )
A.摸出白球 B.摸出红球 C.摸出绿球 D.摸出黑球
8.小刚掷一枚均匀的硬币,一连次都掷出正面朝上,当他第十次掷硬币时,出现正面朝上的概率是( )
A.0 B.1 C. D.
9.如图的四个转盘中,C、D转盘分成8等分,若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是( )
A. B. C. D.
10.从一个不透明的口袋中随机摸出一个球,再放回袋中,不断重复上述过程,一共摸了150次,其中有50次摸到黑球,已知口袋中仅有黑球10个和白球若干个,这些球除颜色外,其他都一样,由此估计口袋中白球的个数约为( )
A.10 B.15 C.20 D.30
11.如图,在3×3的方格中,已有两个小正方形被涂黑,若在其余空白小正方形中任选一个涂黑,则所得图案是一个轴对称图形的概率是( )
A. B. C. D.
12.李老师准备在班内开展“道德”“心理”“安全”三场专题教育讲座,若三场讲座随机安排,则“心理”专题讲座被安排在第一场的概率为( )
A. B. C. D.
二、填空题
13.如图,转盘中6个小扇形的面积都相等,任意转动转盘1次,当转盘停止转动时,指针指向红色区域的概率为 .
14.在相同的条件下,随机抛掷一枚质地均匀的硬币10次,有7次正面向上.当抛掷第11次时,正面向上的概率为 .
15.小明和小丽按如下规则做游戏:桌面上放有7根火柴棒,每次取1根或2根,最后取完者获胜.若由小明先取,且小明获胜是必然事件,则小明第一次应该取走火柴棒的根数是 .
16.在用模拟试验估计40名同学中有两个同学是同一天生日的概率中,将小球每次搅匀的目的是 .
17.一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上,每块地砖的大小、质地完全相同,则该小球停留在阴影部分的概率是 .
三、解答题
18.已知地球表面陆地面积与海洋面积的比约为.如果宇宙中飞来一块陨石落在地球上,“落在陆地上”与“落在海洋里”哪种可能性大?
19.自五月中旬开始,教育局开始组织县域内各校八年级学生进行生物实验加试,某校把参加加试的学生分成5个组,以抽签方式决定各组加试顺序,工作人员准备背面完全一样的5张纸牌,在纸牌的另一面分别写上1,2,3,4,5,将纸牌洗均后背面朝上,由每个组的带队老师随机抽取一张纸牌,请思考以下问题:
(1)抽到的数字有几种可能的结果?
(2)抽到纸牌数字是1的概率是多少?
(3)抽到纸牌数字大于3的概率是多少?
20.不透明袋子中装有5个红球、3个绿球,这些球除了颜色外无其他差别.从袋子中随机摸出1个球,“摸出红球”和“摸出绿球”的可能性相等吗?它们的概率分别为多少?
21.甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
22.有一个转盘如图所示,被分成6个大小相同的扇形,颜色分别为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).有下列事件:①指针指向红色;②指针指向绿色;③指针指向黄色;④指针不指向黄色.
(1)在上述事件中,可能性最大的是________,可能性最小的事件是________(填序号);
(2)将上述事件按发生的可能性从小到大的顺序排列________(填序号).
23.小蒙设计了两个抽奖游戏,游戏一是转盘游戏,如图,转盘被等分成了4个扇形,共有红、黄和蓝三种颜色,自由转动转盘,指针停在红色时会得到奖励;游戏二是摸球游戏,袋子里有2个红球、2个黄球和1个蓝球,每个球除颜色外都相同,任意摸出一个球,摸到红球会得到奖励.小雨要参加抽奖游戏,你建议她参加哪一个游戏?请说明理由.
24.某商场进行有奖促销活动,转盘分为5个扇形区域,分别是特等奖、一等奖、二等奖、三等奖及不获奖,制作转盘时,将获奖扇形区域圆心角分配如下表:
奖次 特等奖 一等奖 二等奖 三等奖
圆心角
如果不用转盘,请设计一种等效实验方案(要求写清楚替代工具和实验规则).
《31.2随机事件的概率》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A D C C D B C A C
题号 11 12
答案 C C
1.A
【分析】设小正方形的边长为1,计算出小正方形的面积为1,平行四边形的面积为1,大正方形的面积为8,由此得三角形区域的面积为8-1-1=6,根据概率公式计算飞镖落在三角形区域的概率即可.
【详解】解:设小正方形的边长为1,则小正方形的面积为1,
平行四边形的底边长为1,高为1,则平行四边形的面积为1,
大正方形的边长为,大正方形的面积为8,
则三角形区域的面积为8-1-1=6,飞镖落在三角形区域的概率为,
故选:A.
【点睛】此题考查了求简单事件的概率,正确理解图形中各小图形的边长的关系及面积的计算方法是解题的关键.
2.A
【分析】求出阴影部分的面积占大正方形的份数即可判断.
【详解】解:∵两个小正方形的面积为和,
∴两个小正方形的边长为和,
∴大正方形的边长为,
∴大正方形的面积为,
∴阴影部分的面积为,
∴米粒落在图中阴影部分的概率为,
故选:A.
【点睛】本题主要考查了几何概率,熟练掌握正方形边长与面积的关系是解题关键.
3.D
【分析】先确定组合的总数,再确定能判定是正方形的组合数,根据概率公式计算即可.
【详解】一共有①②,①③,①④,②③,②④;③④6种组合数,
其中能判定四边形是正方形有①②,①③,②④,③④4种组合数,
所以能判定平行四边形ABCD是正方形的概率是,
故选D.
【点睛】本题考查了概率公式计算,熟练掌握正方形的判定是解题的关键.
4.C
【分析】本题主要考查了简单的概率计算,解题的关键在于能够熟练掌握概率计算公式.
根据一共有4个答案,那么就有4种等可能性的结果,其中只有1个正确答案,那么只有一种是正确的结果,由此利用概率公式计算即可.
【详解】解:∵一共有4个答案,其中只有1个正确答案,
∴选择正确的概率是.
故选C.
5.C
【分析】根据简单事件的概率计算公式即可得.
【详解】解:由题意得:从不透明的袋中随机摸出1个球共有5种等可能性的结果,其中,摸出红球的结果有2种,
则从中随机摸出1个球,摸出红球的概率是,
故选:C.
【点睛】本题考查了求概率,熟练掌握概率公式是解题关键.
6.D
【分析】苍蝇停在白色区域上的概率等于白砖的面积除以整个墙面的面积..
【详解】如图,把墙面上一块砖的面积看成1,墙的面积是9,白砖的面积是6
∴苍蝇停在白色区域上的概率=
故选D
【点睛】本题考查了几何概率,熟练掌握几何概率的计算方法是解题的关键.
7.B
【分析】本题考查了概率,熟练掌握概率公式是解题关键.分别求出摸出四种颜色球的概率,即可得到答案.
【详解】解:A、摸出白球的概率为,不符合题意;
B、摸出红球,符合题意;
C、摸出绿球,不符合题意;
D、摸出黑球,不符合题意;
故选:B.
8.C
【详解】小刚掷一枚硬币,他第十次掷硬币,出现正面朝上还是反而朝上,与前面九次没有任何联系,这十次掷硬币,是十个相互独立的事件,每一次正面朝上与反面朝上,都是概率相同的.故选C.
9.A
【详解】解:A.如图所示:指针落在阴影区域内的概率为:;
B.如图所示:指针落在阴影区域内的概率为:;
C.如图所示:指针落在阴影区域内的概率为:;
D.如图所示:指针落在阴影区域内的概率为:,
∵,
∴指针落在阴影区域内的概率最大的转盘是:.
故选:A.
【点睛】本题考查几何概率.
10.C
【解析】略
11.C
【分析】分别把7个空白处涂黑,判断所得图案是否为轴对称图形,再根据概率公式进行计算.
【详解】在其余空白小正方形中任选一个涂黑,
如上图,把①②③处任意一处涂黑时,图案为轴对称图形,
故所得图案是一个轴对称图形的概率.
故选:C.
【点睛】本题考查了概率公式,轴对称图形.熟记概率公式和能识别轴对称图形是解决此题的关键.
12.C
【分析】利用概率公式求解即可求得答案.
【详解】解: 班内开展“道德”“心理”“安全”三场专题教育讲座,
“心理”专题讲座被安排在第一场的概率.
故选:C.
【点睛】本题主要考查了概率公式的应用,用到的知识点为:概率=所求情况数与总情况数之比,掌握概率公式是解题的关键.
13..
【详解】试题分析:∵圆被等分成6份,其中红色部分占2份,∴落在阴影区域的概率==,故答案为.
考点:几何概率.
14.
【分析】掷一枚质地均匀的硬币,有两种结果,正面或反面朝上,每种结果等可能出现,利用概率公式即可求得答案.
【详解】解:∵掷一枚质地均匀的硬币,有两种结果:正面朝上,反面朝上,每种结果等可能出现,∴她第11次掷这枚硬币时,正面向上的概率是:,
故答案为:.
【点睛】此题考查了概率公式,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.
15.1
【详解】【分析】要保证小明获胜是必然事件,则小明必然要取到第7根火柴,进行倒推,可以发现只要两人所取的根数之和为3就能保证小明获胜.
【详解】如果小明第一次取走1根,剩下了6根,后面无论如取,只要保证每轮两人所取的根数之和为3,就能保证小明将取走最后一根火柴,
而6是3的倍数,因此小明第一次应该取走1根,
故答案为1.
【点睛】本题考查了随机事件,概率的意义,理解题目信息,判断出使两人所取的根数之和是3是解题的关键.
16.使每个球出现的机会均等
【分析】根据概率的等可能性判断即可.
【详解】解:每次模拟试验后将小球每次搅匀是为了使每个球出现的机会均等,
故答案为:使每个球出现的机会均等.
【点睛】本题考查了概率的等可能性,确保等可能性是解题的关键.
17.
【分析】本题考查几何概率模型,用阴影部分的面积除以总面积得到该小球停留在阴影部分的概率即可得到答案.熟记几何概率模型求概率的方法:概率阴影部分面积总面积.
【详解】
解:设图中一个阴影部分三角形的面积为,由图可知它为一个小正方形面积的,
所以所有阴影部分的面积是,大正方形的面积是个小正方形面积,即,
该小球停留在阴影部分的概率是,
故答案为:.
18.“落在海洋里”的可能性更大.
【分析】据几何概率的求法:看海洋的面积占总面积的多少即为所求的概率.
【详解】解:根据题意可得:地球表面陆地面积与海洋面积的比约为3:7,
即相当于将地球总面积分为10份,海洋占7份,
所以落在海洋里的概率是.
所以 “落在海洋里”的可能性更大.
【点睛】本题考查了几何概率的求法,理解题意是解题的关键.首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.
19.(1)有5种结果
(2)
(3)
【分析】本题考查了简单事件的概率,求出所有可能结果数及事件发生的可能结果数,即可求得概率.
(1)根据纸牌数即可确定抽到的可能结果数;
(2)由简单事件概率公式即可求解;
(3)由简单事件概率公式即可求解.
【详解】(1)解:背面朝上且完全一样的5张纸牌随机抽取,有5种结果,且被抽取的可能性是相同的.
(2)解:共有5种结果,每种结果出现的可能性是相同的,
所以抽纸牌1的概率为;
(3)解:有5种等可能结果,大于3的有4和5两种结果,
所以抽纸牌大于3的概率为.
20.“摸出红球”与“摸出绿球”的可能性不相等,它们的概率分别为和.
【分析】根据概率=某种颜色的球的个数÷球的总数进行求解即可.
【详解】解:“摸出红球”与“摸出绿球”的可能性不相等,
它们的概率分别为和.
【点睛】本题主要考查了简单的概率计算,解题的关键在于能够熟练掌握相关知识进行求解.
21.甲班成功的机会大,理由见解析.
【分析】首先分别求出在两个班的160厘米以上的女生中抽出一个作为旗手的概率,然后进行比较,哪个大在哪个班成功的机会大.
【详解】∵已经限定在身高160厘米以上的女生中抽选旗手,甲班身高在160厘米以上的女同学3人,乙班身高在160厘米以上的女同学8人,
∴在甲班被抽到的概率为,在乙甲班被抽到的概率为,
∵>,
∴在甲班被抽到的机会大.
22.(1)④;②
(2)②③①④
【分析】分别求出摸出各种颜色球的概率,即可比较出摸出何种颜色球的可能性大.
【详解】(1)∵共3红2黄1绿相等的六部分,
∴①指针指向红色的概率为;
②指针指向绿色的概率为;
③指针指向黄色的概率为;
④指针不指向黄色为,
∴可能性最大的是④,可能性最小的事件是②,
故答案为:④;②;
(2)由(1)得:②<③<①<④,
故答案为:②③①④.
【点睛】本题考查的是可能性大小的判断,解决这类题目要注意具体情况具体对待.用到的知识点为:可能性等于所求情况数与总情况数之比.
23.参加游戏一
【分析】分别求出两种游戏方案中,获奖的概率,进而比较即可
【详解】游戏一:转盘分为四等分,红色占两份,
∴获奖概率为
游戏二:共有五个球,摸出一个球是红色的概率为
故选择游戏一获奖概率更大.
【点睛】本题考查了概率,熟练掌握等可能事件的概率公式是解题的关键.
24.见解析
【分析】根据扇形圆心角度数可得出各种奖项所占比例,进而利用抽签方式得出等效试验方案.
【详解】解:由题意可得出:
可采取“抓阄”或“抽签”等方法替代,
例如在一个不透明的箱子里放进36个除标号不同外,其他均一样的乒乓球,
其中1个标“特”,2个标“一”,3个标“二”,9个标“三”,其余不标数字,
摸出标有哪个奖次的乒乓球,则获相应的等级的奖品.
【点睛】此题主要考查了模拟实验,替代实验的设计方案很多,但要抓住问题的实质,即各奖项发生的概率要保持不变.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
