10.3三角形的角平分线、中线和高线同步练习(含解析)
文档属性
| 名称 | 10.3三角形的角平分线、中线和高线同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 21:38:01 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
10.3三角形的角平分线、中线和高线
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列说法中错误的是( )
A.三角形的高、中线、角平分线都是线段 B.三角形的三条中线都在三角形内部
C.锐角三角形的三条中线一定交于同一点 D.三角形的三条高交于同一点
2.如图,在中,是高,是中线,,,则的长为( )
A. B.3 C.4 D.6
3.如图,已知,,垂足分别是C,D,其中,,,那么点C到的距离是( )
A.3 B.4 C. D.
4.如图,在中,点在边上,并给出部分数据,则是的( )
A.角平分线 B.中线 C.高线 D.垂直平分线
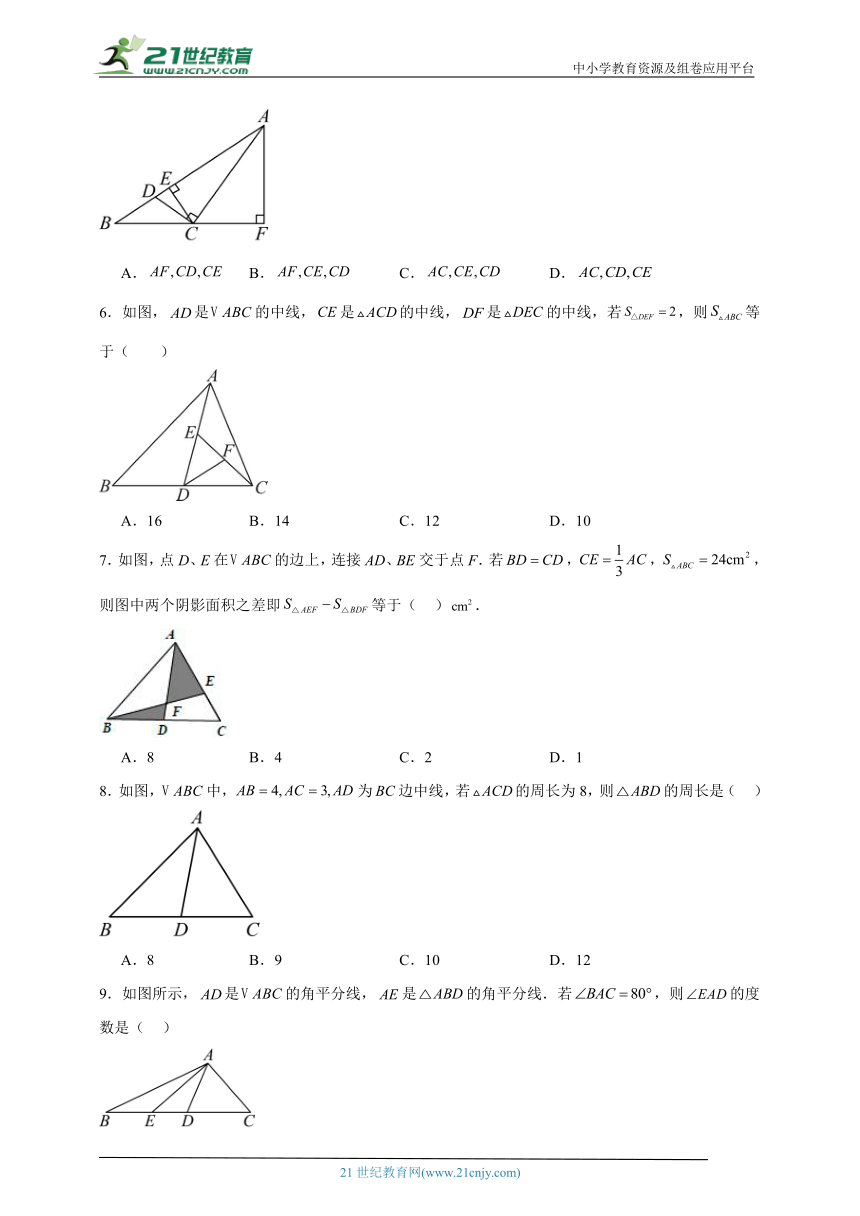
5.如图,中边上的高、中边上的高、中边上的高分别是( )
A. B. C. D.
6.如图,是的中线,是的中线,是的中线,若,则等于( )
A.16 B.14 C.12 D.10
7.如图,点D、E在的边上,连接AD、BE交于点F.若,,,则图中两个阴影面积之差即等于( ).
A.8 B.4 C.2 D.1
8.如图,中,为边中线,若的周长为8,则的周长是( )
A.8 B.9 C.10 D.12
9.如图所示,是的角平分线,是的角平分线.若,则的度数是( )
A. B. C. D.
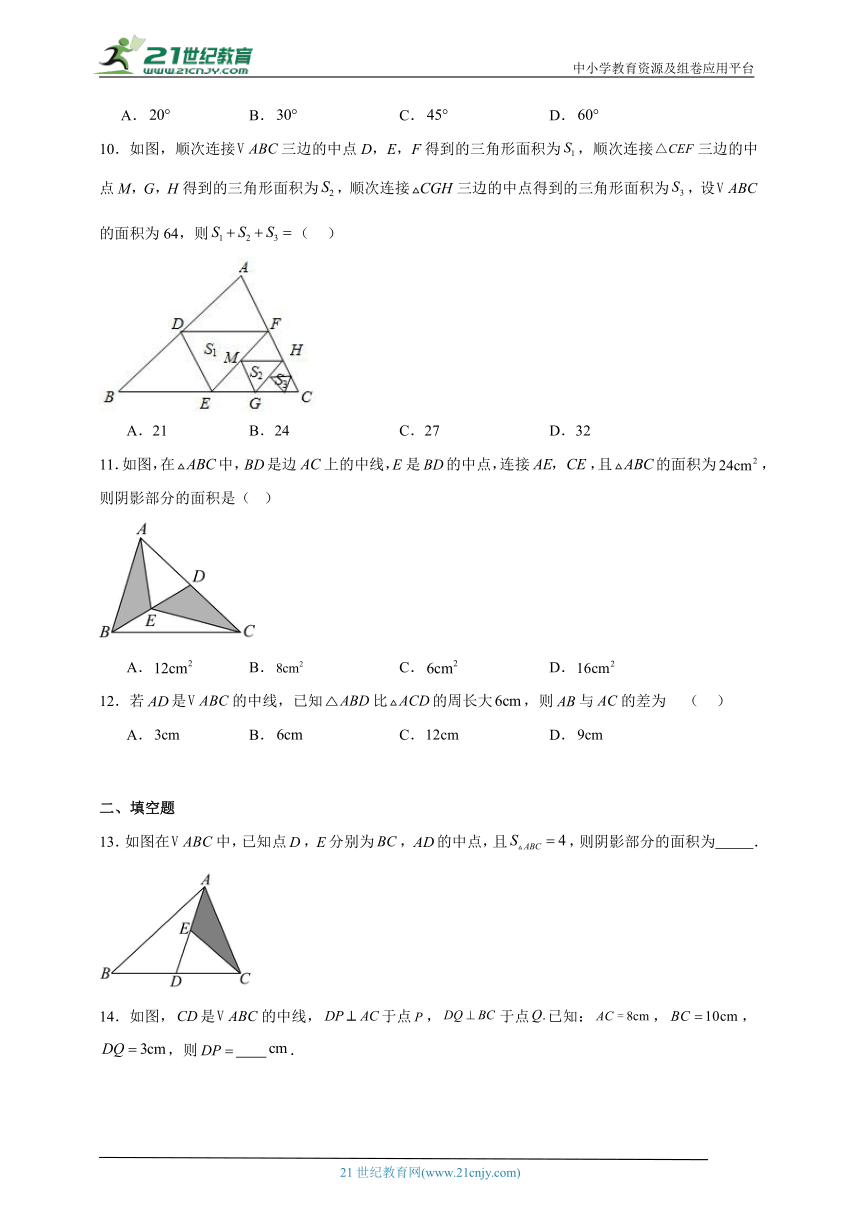
10.如图,顺次连接三边的中点D,E,F得到的三角形面积为,顺次连接三边的中点M,G,H得到的三角形面积为,顺次连接三边的中点得到的三角形面积为,设的面积为64,则( )
A.21 B.24 C.27 D.32
11.如图,在中,是边上的中线,E是的中点,连接,且的面积为,则阴影部分的面积是( )
A. B. C. D.
12.若是的中线,已知比的周长大,则与的差为 ( )
A. B. C. D.
二、填空题
13.如图在中,已知点,分别为,的中点,且,则阴影部分的面积为 .
14.如图,是的中线,于点,于点已知:,,,则 .
15.如图,在中,D,E分别是BC,AD的中点,则 .若,则 .
16.如图,中,点D、E、F分别在三边上,E是的中点,,,交于一点G,,,,则的面积是 .
17.在如图所示的的三条高中,其中边上的高是线段
三、解答题
18.如图,在平面直角坐标系中,点和点分别在轴、轴上移动,是的平分线,是的平分线,是与的交点.在移动过程中,的大小是否发生变化?如果保持不变,请求出的度数;如果发生变化,请求出变化范围.
19.已知(如图).
(1)用刻度尺画AC边上的中线.
(2)用量角器画的平分线.
(3)用三角尺画BC边上的高线.
20.如图所示,为的边上中线,的周长比的周长大,,求边的长.
21.如图,与的角平分线交于点,与相交于点,交于点、交于.
(1)若,,求的度数;
(2)猜想,,的等量关系,直接写出结果.
22.如图,在中,,边上的高,点为上一点,于点,于点.求的值.
23.如图,在中,,为AB边上的高,平分,分别交,于点F,E.
(1)若,求的度数;
(2)与相等吗?请说明理由.
24.如图,已知,根据下列要求作图并回答问题:
(1)作边上的高;
(2)过点D作直线的垂线,垂足为E;
(3)点B到直线的距离是线段_______的长度,(不要求写画法,只需写出结论即可)
《10.3三角形的角平分线、中线和高线》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D B B A B B A A
题号 11 12
答案 A B
1.D
【分析】根据三角形的高线、中线、角平分线即可解答.
【详解】解: 三角形的高、中线、角平分线都是线段,此说法正确,故项不符合题意;
三角形的三条中线都在三角形内部,此说法正确,故不符合题意;
锐角三角形的三条中线一定交于同一点,此说法正确,故不符合题意;
三角形的三条高线所在的直线交于一点,故符合题意.
故选.
【点睛】本题考查了三角形的高线、中线、角平分线的概念,理解三角形的高线、中线、角平分线的概念是解题的关键.
2.B
【分析】本题考查了三角形的高线和中线的意义,根据和求出,根据是中线即可求解.
【详解】解:∵,,
∴
∵是中线,
∴
故选:B
3.D
【分析】本题考查了三角形的面积;
根据三角形面积的不同计算方法列式求解即可.
【详解】解:因为
所以,即,
∴,即点C到的距离是,
故选:D.
4.B
【分析】根据三角形的中线的定义求解即可.
【详解】解:∵,
∴是的中线,
故选:B.
【点睛】本题考查三角形的中线,熟练掌握连接三角形一边的中点与这边所对角的顶点的线段叫三角形的中线是解题的关键.
5.B
【分析】本题考查三角形的高线,根据三角形的高线的定义:从三角形的一个顶点引对边的垂线,顶点与垂足形成的线段,叫做三角形的高,据此进行判断即可.
【详解】解:由图可知:,,
∴是中边上的高,是中边上的高,是中边上的高;
故选C.
6.A
【分析】根据三角形中线平分三角形面积进行求解即可.
【详解】解:∵是的中线,
∴,
∴,
∵是的中线,
∴,
∴,
∵是的中线,
∴,
∴.
故选:A.
【点睛】本题主要考查了三角形中线与三角形的面积关系,关键是掌握三角形中线把三角形面积平分.
7.B
【分析】利用,,求出,再利用求出,再根据,即可求出.
【详解】解:∵,.
∴.
∵.
∴,.
∵.
∴.
故选:B
【点睛】本题考查利用中线求三角形面积,解题的关键是找出.
8.B
【分析】根据的周长为8且,可得,再根据三角形中线的定义和三角形的周长公式解答即可.
【详解】解:∵的周长为8,,
∴,
∴,
∵为边中线,
∴,
∵
∴的周长是;
故选:B.
【点睛】本题考查了三角形的中线和三角形的周长,明确三角形中线的定义是关键.
9.A
【分析】根据,是的角平分线,得出,根据是的角平分线,即可得出.
【详解】解:∵,是的角平分线,
∴,
∵是的角平分线,
∴,
故选:A.
【点睛】本题主要考查了三角形的角平分线,解题的关键是掌握三角形的角平分线将三角形的内角平均为为两份.
10.A
【分析】根据三角形中位线性质证△ADF≌△DBE≌△EFD≌△FEC,求出S1=S△FEC=S=16,S2=S1=4,S3=S2=1.
【详解】解:∵点D,E,F分别是△ABC三边的中点,
∴AD=DB,DF=BC=BE,DE=AC=AF,
在△ADF和△DBE中,
,
∴△ADF≌△DBE(SSS),
同理可证,△ADF≌△DBE≌△EFD≌△FEC,
∴S1=S△FEC=S=16,
同理可得,S2=S1=4,S3=S2=1,
∴S1+S2+S3=16+4+1=21,
故答案为:A.
【点睛】本题考查了三角形中位线.理解三角形中位线性质,证三角形全等是解决问题的关键.
11.A
【分析】本题考查了三角形的中线性质,掌握三角形的中线把三角形的面积分成相等的两个部分是解题的关键.
根据三角形中线,可以知道,,从而计算出答案.
【详解】解:∵是边上的中线,
∴,
∴,
又∵,
∴,
∵是的中点,
,
,
,
故选:A.
12.B
【分析】本题主要考查了三角形的中线定理,根据中线定理得出,再根据周长定义即可求得结果.
【详解】解:如下图:
∵是的中线,
∴
∵比的周长大
∴.
故选∶B.
13.1
【分析】本题考查了与中线有关的三角形面积的计算,由点是的中点得出的面积面积的一半,同理:的面积面积的一半,即的面积的面积,即可得出答案,找准三角形之间的面积关系是解此题的关键.
【详解】解:点是的中点,
,
∴的面积面积的一半,
同理:的面积面积的一半,
即的面积的面积,
∵,
,
故答案为:1.
14.
【分析】由是的中线可得的面积的面积,分别表达两个三角形的面积,代入数据即可得出结论.
【详解】解:∵是的中线,
∴,
∴,
∵,,,
∴,
解得.
故答案为:.
【点睛】此题考查了三角形面积:三角形的面积等于底边长与高线乘积的一半,即底高;三角形的中线将三角形分成面积相等的两部分,解题的关键是掌握三角形中线及其应用.
15. 1
【分析】根据“等底同高”可以得出三角形面积之间的关系.
【详解】解:∵D是BC的中点,三角形的面积=底高
∴
故:的底相等,高相同
∴
∵
∴
∵
∴
故答案为:;1
【点睛】本题考查三角形的中线与面积之间的关系.寻找三角形底、高之间的关系是解题关键.
16.30
【分析】根据两个三角形的高相同时,面积的比等于它们的底边的比,求出,的大小,进而求出的大小;然后根据三角形的中线将三角形分成面积相等的两部分,用的面积乘以2,求出的面积即可.
【详解】解:∵,
∴;
∵E是的中点,
∴,
∴
,
∵是的中线,
∴的面积是:.
故答案为:30.
【点睛】此题主要考查了三角形的面积的求法,以及三角形的中线的特征,解答此题的关键是要明确:三角形的中线将三角形分成面积相等的两部分;两个三角形的高相同时,面积的比等于它们的底边的比.
17./
【分析】本题考查三角形的高线,根据三角形高线定义“从三角形一个顶点向它的对边作垂线,顶点和垂足间的线段叫做三角形该边的高线”即可判断.
【详解】解:∵为钝角是三角形,,
∴为边上的高.
故答案为:.
18.不变,
【分析】由角平分线的定义可得,,从而得到,再由三角形内角和定理可得,即可得到答案.
【详解】解:在移动过程中,的大小保持不变.
是的平分线,是的平分线,
,,
,
,
,
在移动过程中,的大小保持不变,为.
【点睛】本题考查了角平分线的定义、三角形内角和定理,熟练掌握角平分线的定义、三角形内角和定理是解题的关键.
19.(1)见解析;
(2)见解析;
(3)见解析.
【分析】(1)用刻度尺找到的中点,连接即可;
(2)用量角器测量的度数,画出线段平分,即可;
(3)过点作,交延长线于点,即可.
【详解】(1)解:用刻度尺找到的中点,连接,
则为边的上的中线;
(2)用量角器测量的度数,画出线段平分,则线段为的角平分线;
(3)过点作,交延长线于点,为垂足,则为边上的高.
【点睛】此题考查了作三角形的中线,角平分线和高,解题的关键是掌握三角形的中线,角平分线和高的定义.
20.
【分析】根据中线的定义得出,根据的周长比的周长大,推出
,即可求解.
【详解】解:∵为的边上中线,
∴,
∵的周长比的周长大,
∴,
即,
又∵,
∴.
【点睛】本题主要考查了三角形中线的定义,解题的关键是掌握三角形一个顶点和对边中点的连线是三角形的中线.
21.(1)
(2)
【分析】(1)设,,根据角平分线的定义得出,,根据三角形内角和定理得出①.根据三角形外角的性质得出②.③,进而得出;
(2)由(1)同理可知:,即可求解.
【详解】(1)解:设,,
根据和的角平分线相交于点可知:
,,
三角形的内角和等于,,,
,即①.
是与的外角,
,即②.
同理,是与的外角,
,即③,
①②得,④,
①③得,⑤,
④代入⑤得,,
,
解得;
(2),理由如下:
由(1)同理可知:
,
解得:.
【点睛】本题考查了三角形的角平分线,三角形的外角的性质,熟练掌握三角形的外角的性质是解题的关键.
22.4
【分析】本题考查了三角形的面积,与高有关的计算,正确掌握相关性质内容是解题的关键.因为边上的高,则,结合,故,因为,得,即可作答.
【详解】解:如图,连结.
边上的高,
∴,
∵于点,于点.
∴,,
∵,
.
又,
,
.
23.(1)10°
(2)相等,理由见解析
【分析】本题考查了直角三角形的性质、三角形角平分线、中线和高的有关知识.
(1)根据直角三角形的性质得出∠CBE,进而利用角平分线的定义和三角形内角和定理解答即可,
(2)题目中有两对直角,可得两对角互余,由角平分线及对顶角可得两对角相等,然后利用等量代换可得答案.
【详解】(1)解:∵,,
∴,
∵平分,
∴,
∴.
(2)如下图:
∵,
∴,
∵,
∴,
又∵平分,
∴,
∴,
∵,
∴,
即.
24.(1)见解析
(2)见解析
(3)
【分析】(1)根据三角形高的定义画出图形即可.
(2)根据垂线的定义画出图形即可.
(3)根据点到直线的距离,判断即可.
【详解】(1)解:如图,线段即为所求.
(2)如图,线段即为所求.
(3)到直线的距离是线段的长度.
故答案为:.
【点睛】本题考查作图基本作图,点到直线的距离等知识,解题的关键是理解三角形高的定义,垂线的定义,属于中考常考题型.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
10.3三角形的角平分线、中线和高线
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列说法中错误的是( )
A.三角形的高、中线、角平分线都是线段 B.三角形的三条中线都在三角形内部
C.锐角三角形的三条中线一定交于同一点 D.三角形的三条高交于同一点
2.如图,在中,是高,是中线,,,则的长为( )
A. B.3 C.4 D.6
3.如图,已知,,垂足分别是C,D,其中,,,那么点C到的距离是( )
A.3 B.4 C. D.
4.如图,在中,点在边上,并给出部分数据,则是的( )
A.角平分线 B.中线 C.高线 D.垂直平分线
5.如图,中边上的高、中边上的高、中边上的高分别是( )
A. B. C. D.
6.如图,是的中线,是的中线,是的中线,若,则等于( )
A.16 B.14 C.12 D.10
7.如图,点D、E在的边上,连接AD、BE交于点F.若,,,则图中两个阴影面积之差即等于( ).
A.8 B.4 C.2 D.1
8.如图,中,为边中线,若的周长为8,则的周长是( )
A.8 B.9 C.10 D.12
9.如图所示,是的角平分线,是的角平分线.若,则的度数是( )
A. B. C. D.
10.如图,顺次连接三边的中点D,E,F得到的三角形面积为,顺次连接三边的中点M,G,H得到的三角形面积为,顺次连接三边的中点得到的三角形面积为,设的面积为64,则( )
A.21 B.24 C.27 D.32
11.如图,在中,是边上的中线,E是的中点,连接,且的面积为,则阴影部分的面积是( )
A. B. C. D.
12.若是的中线,已知比的周长大,则与的差为 ( )
A. B. C. D.
二、填空题
13.如图在中,已知点,分别为,的中点,且,则阴影部分的面积为 .
14.如图,是的中线,于点,于点已知:,,,则 .
15.如图,在中,D,E分别是BC,AD的中点,则 .若,则 .
16.如图,中,点D、E、F分别在三边上,E是的中点,,,交于一点G,,,,则的面积是 .
17.在如图所示的的三条高中,其中边上的高是线段
三、解答题
18.如图,在平面直角坐标系中,点和点分别在轴、轴上移动,是的平分线,是的平分线,是与的交点.在移动过程中,的大小是否发生变化?如果保持不变,请求出的度数;如果发生变化,请求出变化范围.
19.已知(如图).
(1)用刻度尺画AC边上的中线.
(2)用量角器画的平分线.
(3)用三角尺画BC边上的高线.
20.如图所示,为的边上中线,的周长比的周长大,,求边的长.
21.如图,与的角平分线交于点,与相交于点,交于点、交于.
(1)若,,求的度数;
(2)猜想,,的等量关系,直接写出结果.
22.如图,在中,,边上的高,点为上一点,于点,于点.求的值.
23.如图,在中,,为AB边上的高,平分,分别交,于点F,E.
(1)若,求的度数;
(2)与相等吗?请说明理由.
24.如图,已知,根据下列要求作图并回答问题:
(1)作边上的高;
(2)过点D作直线的垂线,垂足为E;
(3)点B到直线的距离是线段_______的长度,(不要求写画法,只需写出结论即可)
《10.3三角形的角平分线、中线和高线》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D B B A B B A A
题号 11 12
答案 A B
1.D
【分析】根据三角形的高线、中线、角平分线即可解答.
【详解】解: 三角形的高、中线、角平分线都是线段,此说法正确,故项不符合题意;
三角形的三条中线都在三角形内部,此说法正确,故不符合题意;
锐角三角形的三条中线一定交于同一点,此说法正确,故不符合题意;
三角形的三条高线所在的直线交于一点,故符合题意.
故选.
【点睛】本题考查了三角形的高线、中线、角平分线的概念,理解三角形的高线、中线、角平分线的概念是解题的关键.
2.B
【分析】本题考查了三角形的高线和中线的意义,根据和求出,根据是中线即可求解.
【详解】解:∵,,
∴
∵是中线,
∴
故选:B
3.D
【分析】本题考查了三角形的面积;
根据三角形面积的不同计算方法列式求解即可.
【详解】解:因为
所以,即,
∴,即点C到的距离是,
故选:D.
4.B
【分析】根据三角形的中线的定义求解即可.
【详解】解:∵,
∴是的中线,
故选:B.
【点睛】本题考查三角形的中线,熟练掌握连接三角形一边的中点与这边所对角的顶点的线段叫三角形的中线是解题的关键.
5.B
【分析】本题考查三角形的高线,根据三角形的高线的定义:从三角形的一个顶点引对边的垂线,顶点与垂足形成的线段,叫做三角形的高,据此进行判断即可.
【详解】解:由图可知:,,
∴是中边上的高,是中边上的高,是中边上的高;
故选C.
6.A
【分析】根据三角形中线平分三角形面积进行求解即可.
【详解】解:∵是的中线,
∴,
∴,
∵是的中线,
∴,
∴,
∵是的中线,
∴,
∴.
故选:A.
【点睛】本题主要考查了三角形中线与三角形的面积关系,关键是掌握三角形中线把三角形面积平分.
7.B
【分析】利用,,求出,再利用求出,再根据,即可求出.
【详解】解:∵,.
∴.
∵.
∴,.
∵.
∴.
故选:B
【点睛】本题考查利用中线求三角形面积,解题的关键是找出.
8.B
【分析】根据的周长为8且,可得,再根据三角形中线的定义和三角形的周长公式解答即可.
【详解】解:∵的周长为8,,
∴,
∴,
∵为边中线,
∴,
∵
∴的周长是;
故选:B.
【点睛】本题考查了三角形的中线和三角形的周长,明确三角形中线的定义是关键.
9.A
【分析】根据,是的角平分线,得出,根据是的角平分线,即可得出.
【详解】解:∵,是的角平分线,
∴,
∵是的角平分线,
∴,
故选:A.
【点睛】本题主要考查了三角形的角平分线,解题的关键是掌握三角形的角平分线将三角形的内角平均为为两份.
10.A
【分析】根据三角形中位线性质证△ADF≌△DBE≌△EFD≌△FEC,求出S1=S△FEC=S=16,S2=S1=4,S3=S2=1.
【详解】解:∵点D,E,F分别是△ABC三边的中点,
∴AD=DB,DF=BC=BE,DE=AC=AF,
在△ADF和△DBE中,
,
∴△ADF≌△DBE(SSS),
同理可证,△ADF≌△DBE≌△EFD≌△FEC,
∴S1=S△FEC=S=16,
同理可得,S2=S1=4,S3=S2=1,
∴S1+S2+S3=16+4+1=21,
故答案为:A.
【点睛】本题考查了三角形中位线.理解三角形中位线性质,证三角形全等是解决问题的关键.
11.A
【分析】本题考查了三角形的中线性质,掌握三角形的中线把三角形的面积分成相等的两个部分是解题的关键.
根据三角形中线,可以知道,,从而计算出答案.
【详解】解:∵是边上的中线,
∴,
∴,
又∵,
∴,
∵是的中点,
,
,
,
故选:A.
12.B
【分析】本题主要考查了三角形的中线定理,根据中线定理得出,再根据周长定义即可求得结果.
【详解】解:如下图:
∵是的中线,
∴
∵比的周长大
∴.
故选∶B.
13.1
【分析】本题考查了与中线有关的三角形面积的计算,由点是的中点得出的面积面积的一半,同理:的面积面积的一半,即的面积的面积,即可得出答案,找准三角形之间的面积关系是解此题的关键.
【详解】解:点是的中点,
,
∴的面积面积的一半,
同理:的面积面积的一半,
即的面积的面积,
∵,
,
故答案为:1.
14.
【分析】由是的中线可得的面积的面积,分别表达两个三角形的面积,代入数据即可得出结论.
【详解】解:∵是的中线,
∴,
∴,
∵,,,
∴,
解得.
故答案为:.
【点睛】此题考查了三角形面积:三角形的面积等于底边长与高线乘积的一半,即底高;三角形的中线将三角形分成面积相等的两部分,解题的关键是掌握三角形中线及其应用.
15. 1
【分析】根据“等底同高”可以得出三角形面积之间的关系.
【详解】解:∵D是BC的中点,三角形的面积=底高
∴
故:的底相等,高相同
∴
∵
∴
∵
∴
故答案为:;1
【点睛】本题考查三角形的中线与面积之间的关系.寻找三角形底、高之间的关系是解题关键.
16.30
【分析】根据两个三角形的高相同时,面积的比等于它们的底边的比,求出,的大小,进而求出的大小;然后根据三角形的中线将三角形分成面积相等的两部分,用的面积乘以2,求出的面积即可.
【详解】解:∵,
∴;
∵E是的中点,
∴,
∴
,
∵是的中线,
∴的面积是:.
故答案为:30.
【点睛】此题主要考查了三角形的面积的求法,以及三角形的中线的特征,解答此题的关键是要明确:三角形的中线将三角形分成面积相等的两部分;两个三角形的高相同时,面积的比等于它们的底边的比.
17./
【分析】本题考查三角形的高线,根据三角形高线定义“从三角形一个顶点向它的对边作垂线,顶点和垂足间的线段叫做三角形该边的高线”即可判断.
【详解】解:∵为钝角是三角形,,
∴为边上的高.
故答案为:.
18.不变,
【分析】由角平分线的定义可得,,从而得到,再由三角形内角和定理可得,即可得到答案.
【详解】解:在移动过程中,的大小保持不变.
是的平分线,是的平分线,
,,
,
,
,
在移动过程中,的大小保持不变,为.
【点睛】本题考查了角平分线的定义、三角形内角和定理,熟练掌握角平分线的定义、三角形内角和定理是解题的关键.
19.(1)见解析;
(2)见解析;
(3)见解析.
【分析】(1)用刻度尺找到的中点,连接即可;
(2)用量角器测量的度数,画出线段平分,即可;
(3)过点作,交延长线于点,即可.
【详解】(1)解:用刻度尺找到的中点,连接,
则为边的上的中线;
(2)用量角器测量的度数,画出线段平分,则线段为的角平分线;
(3)过点作,交延长线于点,为垂足,则为边上的高.
【点睛】此题考查了作三角形的中线,角平分线和高,解题的关键是掌握三角形的中线,角平分线和高的定义.
20.
【分析】根据中线的定义得出,根据的周长比的周长大,推出
,即可求解.
【详解】解:∵为的边上中线,
∴,
∵的周长比的周长大,
∴,
即,
又∵,
∴.
【点睛】本题主要考查了三角形中线的定义,解题的关键是掌握三角形一个顶点和对边中点的连线是三角形的中线.
21.(1)
(2)
【分析】(1)设,,根据角平分线的定义得出,,根据三角形内角和定理得出①.根据三角形外角的性质得出②.③,进而得出;
(2)由(1)同理可知:,即可求解.
【详解】(1)解:设,,
根据和的角平分线相交于点可知:
,,
三角形的内角和等于,,,
,即①.
是与的外角,
,即②.
同理,是与的外角,
,即③,
①②得,④,
①③得,⑤,
④代入⑤得,,
,
解得;
(2),理由如下:
由(1)同理可知:
,
解得:.
【点睛】本题考查了三角形的角平分线,三角形的外角的性质,熟练掌握三角形的外角的性质是解题的关键.
22.4
【分析】本题考查了三角形的面积,与高有关的计算,正确掌握相关性质内容是解题的关键.因为边上的高,则,结合,故,因为,得,即可作答.
【详解】解:如图,连结.
边上的高,
∴,
∵于点,于点.
∴,,
∵,
.
又,
,
.
23.(1)10°
(2)相等,理由见解析
【分析】本题考查了直角三角形的性质、三角形角平分线、中线和高的有关知识.
(1)根据直角三角形的性质得出∠CBE,进而利用角平分线的定义和三角形内角和定理解答即可,
(2)题目中有两对直角,可得两对角互余,由角平分线及对顶角可得两对角相等,然后利用等量代换可得答案.
【详解】(1)解:∵,,
∴,
∵平分,
∴,
∴.
(2)如下图:
∵,
∴,
∵,
∴,
又∵平分,
∴,
∴,
∵,
∴,
即.
24.(1)见解析
(2)见解析
(3)
【分析】(1)根据三角形高的定义画出图形即可.
(2)根据垂线的定义画出图形即可.
(3)根据点到直线的距离,判断即可.
【详解】(1)解:如图,线段即为所求.
(2)如图,线段即为所求.
(3)到直线的距离是线段的长度.
故答案为:.
【点睛】本题考查作图基本作图,点到直线的距离等知识,解题的关键是理解三角形高的定义,垂线的定义,属于中考常考题型.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
