6.3二元一次方程组的应用同步练习(含解析)
文档属性
| 名称 | 6.3二元一次方程组的应用同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 589.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 22:11:28 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
6.3二元一次方程组的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.为打造成渝地区双城经济圈,成渝高速公路在今年开始打造八车道高速公路通道,其中重庆段从重庆江北区到荣昌区全长约为,若一辆小汽车,一辆货车同时从江北,荣昌两地同时相向开出,经过45分钟相遇,相遇时小汽车比货车多行,设小汽车和货车的速度分别为,,则下列方程组正确的是( )
A. B. C. D.
2.若一个两位数,它的个位上的数字与十位上的数字和为5,则这样的两位数有( )
A.3个 B.4个 C.5个 D.6个
3.某公司有新员工和老员工若干名.已知1名新员工每天制造的零件个数比1名老员工少30,1名新员工与2名老员工每天共可制造180个零件,则1名新员工与1名老员工每天各能制造多少个零件?设1名新员工每天能制造个零件,1名老员工每天能制造个零件.根据题意可列方程组为()
A. B. C. D.
4.植树节这天有20名同学共种了52棵树苗,其中男生每人种树3棵,女生每人种树2棵设男生有人,女生有人,根据题意,下列方程组正确的是( )
A. B. C. D.
5.甲和乙两人玩“打弹珠”游戏,甲对乙说:“把你一半的弹珠给我,我就有35颗弹珠.”乙说:“把你弹珠的给我,我就有40颗弹珠.”若设乙有颗弹珠,甲有颗弹珠,则可列方程组为( )
A. B. C. D.
6.客车和货车分别在两条平行的铁轨上行驶,客车长米,货车长米如果两车相向而行,那么从两车车头相遇到车尾离开共需秒钟;如果客车从后面追货车,那么从客车车头追上货车车尾到客车车尾离开货车车头共需分秒,假设客车和货车每秒钟分别行驶和米,则可列方程组为( )
A. B.
C. D.
7.第二届杭州市月季花展于2024年4月27日在杭州开展,若黄色月季花每支4元,红色月季花每支6元,小明想要花费30元全部用于购买这两个品种的花送给妈妈,那么小明的购买方案有( )
A.1种 B.2种 C.3种 D.4种
8.一个两位数,十位数字比个位数字的2倍大1.若这个两位数减去36恰好等于个位数字与十位数字对调后所得的两位数,则这个两位数是( )
A.86 B.68 C.94 D.73
9.某班的一个综合实践活动小组去甲、乙两个超市调查去年和今年“元旦”期间的销售情况,下面是调查后小明与其他两位同学进行交流的对话.
小明说:“去年两超市的销售额共为150万元,今年两超市的销售额共为170万元.”
小亮说:“甲超市的销售额今年比去年增加.”
小颖说:“乙超市的销售额今年比去年增加.”
根据他们的对话,得出今年甲超市的销售额为( )万元.
A.100 B.50 C.60 D.110
10.文峰超市以同样的价格卖出同样的牙刷和牙膏,以下是4天的记录:第1天,卖出13支牙刷和7盒牙膏,收入144元;第2天,卖出18支牙刷和11盒牙膏,收入219元;第3天,卖出23支牙刷和20盒牙膏,收入368元;第4天,卖出17支牙刷和11盒牙膏,收入216元.已知第1天和第2天的记录无误,第3天和第4天有一天的记录有误,则记录有误的一天收入( )
A.多记1元 B.多记2元 C.少记1元 D.少记2元
11.如图,宽为的矩形图案是由10个形状和大小完全一样的小长方形拼成,则一个小长方形的面积为( )
A. B. C. D.
12.爸爸骑摩托车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下:
时刻 9:00 10:00 11:30
里程碑上的数 是一个两位数,它的两个数字之和是6 是一个两位数,它的十位与个位数字与9:00所看到的正好互换了 是一个三位数,它比9:00时看到的两位数中间多了个0
则10:00时看到里程碑上的数是( )
A.15 B.24 C.42 D.51
二、填空题
13.某市为进一步加快文明城市的建设,园林局尝试种植A、B两种树种.经过试种后发现,种植A种树苗a棵,种下后成活了棵,种植B种树苗b棵,种下后成活了(b-2)棵.第一阶段两种树苗共种植40棵,且两种树苗的成活棵树相同,则种植A种树苗 棵.第二阶段,该园林局又种植A种树苗m棵,B种树苗n棵,若m=2n,在第一阶段的基础上进行统计,则这两个阶段种植A种树苗成活棵数 种植B种树苗成活棵数(填“>”“<”或“=”).
14.我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足.问鸡兔各几何.”设有只鸡,只兔,根据题意,可列方程组为 .
15.某工厂去年的总产值比总支出多500万元,而今年计划的总产值比总支出多950万元,已知今年计划总产值比去年增加15%,而计划总支出比去年减少10%,求去年计划的总产值和总支出各是多少万元?解:设去年计划的总产值、总支出分别是x万元、y万元,根据题意,可列方程组 .
16.中国古代数学著作《九章算术》中记载了这样一个题目:今有共买琎,人出半,盈四;人出少半,不足三.问人数,琎价各几何.其大意是今有人合伙买琎石,每人出钱,会多出4钱;每人出钱,又差了3钱.问人数,琎价各是多少.设人数为,琎价为,则可列方程组为 .
17.如图,在大长方形中不重叠的放入七个长、宽都相同的小长方形,根据图中给出的数据,可得出阴影部分面积为 .
三、解答题
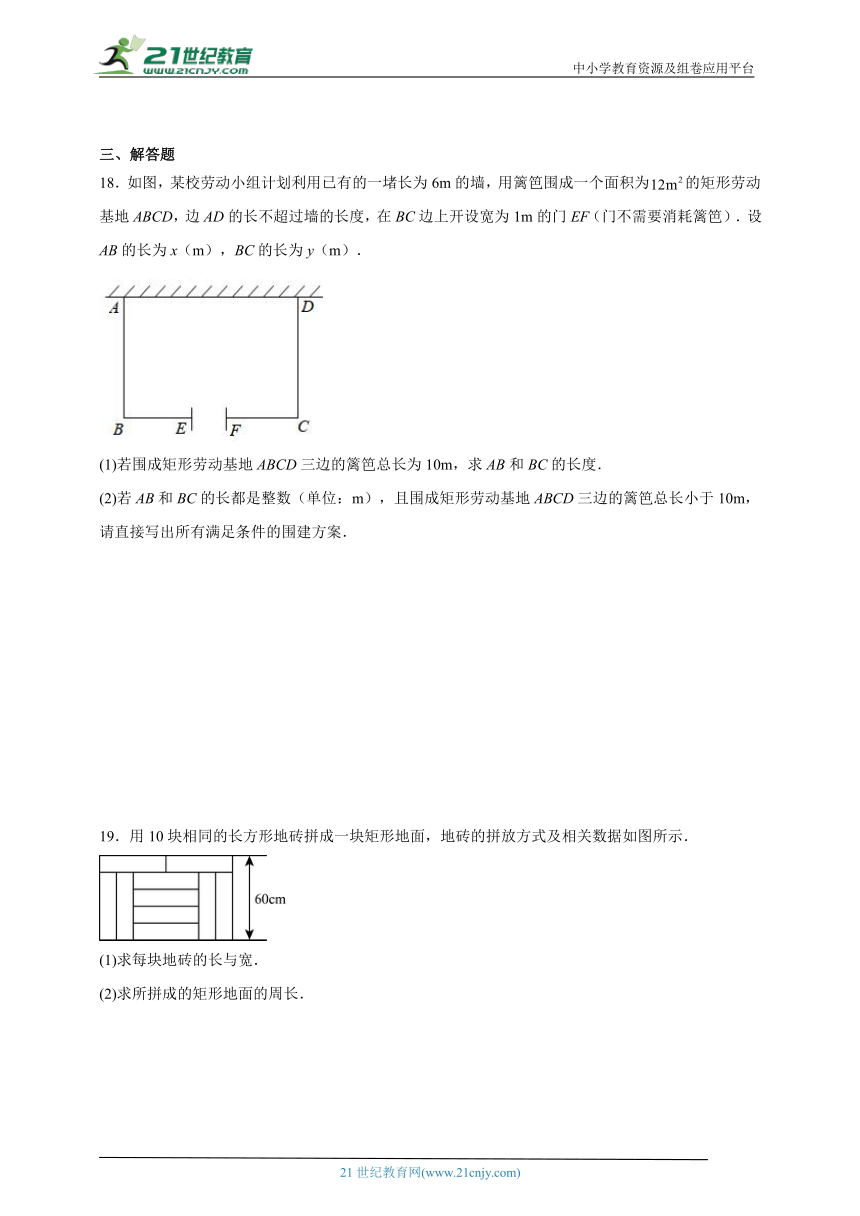
18.如图,某校劳动小组计划利用已有的一堵长为6m的墙,用篱笆围成一个面积为的矩形劳动基地ABCD,边AD的长不超过墙的长度,在BC边上开设宽为1m的门EF(门不需要消耗篱笆).设AB的长为x(m),BC的长为y(m).
(1)若围成矩形劳动基地ABCD三边的篱笆总长为10m,求AB和BC的长度.
(2)若AB和BC的长都是整数(单位:m),且围成矩形劳动基地ABCD三边的篱笆总长小于10m,请直接写出所有满足条件的围建方案.
19.用10块相同的长方形地砖拼成一块矩形地面,地砖的拼放方式及相关数据如图所示.
(1)求每块地砖的长与宽.
(2)求所拼成的矩形地面的周长.
20.阅读感悟:
已知实数x,y满足3x-y=5①,2x+3y=7②,求x-4y和7x+5y的值.
本题常规思路是将①②两式联立组成方程组,解得x,y的值再代入欲求值的式子中得到答案,常规思路运算量比较大.其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得式子的值,如由①-②可得x-4y=-2,由①+②×2可得7x+5y= 19.这样的解题思路就利用了通常所说的“整体思想”.
[解决问题]已知二元一次方程组,则x-y= ,x+y= .
[拓展延伸]某班级组织活动需购买小奖品,买18支铅笔、27本笔记本共需86.4元,买22支铅笔、13本笔记本共需53.6元,则购买5支铅笔、5本笔记本共需多少元?
21.一只小船从港口顺水航行到港口需8小时,而从港口逆水返回到港口需12小时.某日,该小船在早晨8点出发,由港口顺水航行到港口时,发现船上一个救生圈在途中掉入水中,于是立即返回寻找救生圈,4小时后找到救生圈.
(1)若港口到港口的航程为240千米,求水流速度是每小时多少千米?
(2)若救生圈从港口漂流到港口,需要多长时间?
(3)救生圈于何时掉入水中?
22.某服装店用5700元购进A,B两种新式服装,按标价售出后可获得毛利润3600元(毛利润=售价-进价),这两种服装的进价,标价如表所示.
类型价格 A型 B型
进价(元/件) 60 100
标价(元/件) 100 160
(1)请利用二元一次方程组求这两种服装各购进的件数;
(2)如果A种服装按标价的9折出售,B种服装按标价的8折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?
23.随着“低碳生活,绿色出行”理念的普及,某汽车销售公司计划购进一批新能源汽车进行销售.据了解,1辆A型汽车、2辆B型汽车的进价共计110万元;2辆A型汽车、3辆B型汽车的进价共计175万元.
(1)每辆A,B两种型号的汽车进价分别为多少万元?
(2)若该公司计划正好用400万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),则该公司有哪几套方案?
24.现有一辆卡车,要运输若干套某种设备,每套设备由A部件和部件组成.已知3个A部件和2个部件的总质量为7.6吨,5个A部件和3个部件的质量相等.求1个A部件和1个部件的质量各是多少.
《6.3二元一次方程组的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C A D A A B D D C
题号 11 12
答案 A D
1.D
【分析】设小汽车和货车的速度分别为,,根据“全长约为,经过45分钟相遇,相遇时小汽车比货车多行”列方程组即可.
【详解】解:设小汽车和货车的速度分别为,,
45分钟小时,
由题意得:,
故选:D.
【点睛】本题考查了二元一次方程组的应用,找出合适的等量关系列出方程组是解题的关键.
2.C
【分析】根据题意列举出符合条件的数字即可解得.
【详解】解:一个两位数,个位上的数字和十位上的数字合起来是5,这样的两位数有:50,14,41,23,32.
故选:C.
3.A
【分析】本题二元一次方程组的应用,解题的关键是能够根据题意找到两个等量关系,这是列方程的依据.
找到两个等量关系列出方程组即可.
【详解】解:设一个生手工每天能制作x个零件,一个熟手工每天能制造y个零件,
根据题意得:,
故选A.
4.D
【分析】设男生有x人,女生有y人,根据男女生人数为20,共种了52棵树苗,列出方程组成方程组即可.
【详解】解:设男生有x人,女生有y人,
根据题意可得:,
故选:D.
【点睛】本题考查二元一次方程组的实际运用,找出题目蕴含的数量关系是解决问题的关键.
5.A
【分析】本题考查了列二元一次方程组(根据实际问题列二元一次方程组),读懂题意,根据题中的等量关系正确列出方程组是解题的关键.
根据题意即可直接得出答案.
【详解】解:由题意,可列方程组为:
,
故选:.
6.A
【分析】根据题意和题目中的数据,可知,,然后即可列出相应的方程组,本题得以解决.
【详解】解:分秒秒,
由题意可得,
,
故选:A.
【点睛】本题考查由实际问题抽象出二元一次方程组,解答本题的关键是明确题意,列出相应的方程组.
7.B
【分析】本题主要考查了二元一次方程的应用,解题的关键是根据题意列出方程.设黄色月季花x支,红色月季花y支,根据两种花的花费总共为30元,列出方程,解方程即可.
【详解】解:设黄色月季花x支,红色月季花y支,根据题意得:
,
∵x、y为正整数,
∴,,
∴小明的购买方案有2种,
故选:B.
8.D
【分析】本题考查二元一次方程组的实际应用,设十位数字是,个位数字是,由题意列方程组求解即可得到答案,读懂题意,准确列出二元一次方程组是解决问题的关键.
【详解】解:设十位数字是,个位数字是,
则,
解得,
原来的两位数是,
故选:D.
9.D
【分析】设甲超市去年销售额为x万元,乙超市去年销售额为y万元,根据题意列出方程组求解后,再求出甲超市今年的销售额即可.
【详解】解:设甲超市去年销售额为x万元,乙超市去年销售额为y万元,
根据题意,得:
,,
,
解得:,
所以今年甲超市销售额为.
故选:D.
【点睛】本题考查了二元一次方程组的应用,解决本题的关键是根据题意找到等量关系.
10.C
【解析】略
11.A
【分析】本题主要考查了二元一次方程组的实际应用,根据题意找到等量关系列出方程组是解题的关键.设小长方形的宽为,长为,再根据题意列方程组求得、,最后求面积即可.
【详解】解:设小长方形的宽为,长为,
根据题意得, ,
解得,
一个小长方形的面积为.
故选:A.
12.D
【分析】解:设小明9:00看到的两位数,十位数为x,个位数为y,根据车的速度不变和12:00时看到的两位数字之和为6,即可列出二元一次方程组,解方程组即可求解.
【详解】解:设小明9:00看到的两位数,十位数为x,个位数为y,由题意列方程组得:,
解得:,
∴9:00时看到的两位数是15.
10:00时看到里程碑上的数是
故选:D
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题关键.
13. 22 >
【详解】解:第一阶段,依题意得:,
解得:,
则种植A种树苗22棵;
第二阶段,∵种植A种树苗m棵,B种树苗n棵,若m=2n,
∴A种树苗成活了 n+5(棵),
B种树苗成活了n-2(棵),
∴这两个阶段A种树苗共成活了×22+5+ n+5= n+21(棵),
B种树苗共成活了18-2+ n-2= n+14(棵),
∵n+21> n+14,
∴这两个阶段A种树苗共成活棵数>B种树苗共成活棵数,
故答案为:>.
【点睛】本题考查了二元一次方程组的应用,列代数式,整式的加减运算,找准等量关系,正确列出二元一次方程组是解题的关键.
14.
【分析】根据“鸡的数量兔的数量,鸡的脚的数量兔子的脚的数量”可列方程组.
【详解】解:根据题意可得:,
故答案为:.
【点睛】本题考查由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,找出等量关系,列出相应的方程组.
15.
【分析】设去年计划的总产值是x万元,总支出y万元.根据“去年的总产值比总支出多500万元.由于今年总产值比去年增加15%,总支出比去年节约10%,因此,今年总产值比总支出多950万元”列方程组.
【详解】解:设去年计划的总产值是x万元,总支出y万元.根据题意,得
,
故答案为:.
【点睛】考查了二元一次方程组的应用,根据实际问题中的条件列方程时,要注意抓住题目中的一些关键性词语,找出等量关系,列出方程.
16.
【分析】本题考查了二元一次方程组的应用(古代问题),读懂题意,根据题中的等量关系正确列出方程组是解题的关键.
根据题意即可直接得出答案.
【详解】解:由题意,可列方程组为:
,
故答案为:.
17.
【分析】设小长方形的长为a,宽为b,观察图形,根据各边之间的关系,可得出关于a,b的二元一次方程组,解之可求出a,b的值,再利用阴影部分的面积=大长方形的面积-7×小长方形的面积,即可求出结论.
【详解】设小长方形的长为a,宽为b,
根据题意得:,
解得:,
∴阴影部分面积为:,
故答案为:.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
18.(1)AB=4,BC=3
(2)AB=2,BC=6或AB=3,BC=4
【分析】(1)根据;篱笆总长和门的长表示出AB、BC,列出方程即可.
(2)根据围成矩形三边的篱笆总长小于10列出不等式,再由x和y为整数且xy=12确定出满足题意的方案.
【详解】(1)根据题意得:,即.
代入得:,整理得:.
解得:或.
当时,,不符合题意;当时,,符合题意.
则AB=4,BC=3.
(2)根据题意得:,即.
∵AB,BC为整数,即x,y为整数,且.
∴当y=6时,x=2;当y=4时,x=3.
则满足条件的围建方案为:AB=2,BC=6或AB=3,BC=4.
【点睛】本题考查了一元二次方程的应用,弄清题意是解题的关键.
19.(1)每块地砖的长与宽分别为和
(2)所拼成的矩形地面的周长是
【分析】本题考查了二元一次方程组的应用,通过理解题意和观察图示可知本题存在两个等量关系是解题的关键.
(1)设每块地砖的长与宽分别为,根据图中关系可得,解方程组即可;
(2)由矩形周长公式求解.
【详解】(1)解:设每块地砖的长与宽分别为,
由题意得:,
解得:,
∴每块地砖的长与宽分别为和;
(2)解:所拼成的矩形地面的周长,
答:所拼成的矩形地面的周长是.
20.2;4;购买5支铅笔、5本笔记本共需17.5元
【分析】[解决问题]分别② ①,①+②即可求得;
[拓展延伸]设每只铅笔x元,每本笔记本y元,根据题意列出方程组,然后求得5(x+y)的值即可.
【详解】解:[解决问题],
② ①,得2x 2y=2,
即x y=4;
①+②,得4x+4y=16,
即x+y=4,
故答案为:2,4.
[拓展延伸]设每只铅笔x元,每本笔记本y元,
根据题意,得,
①+②,得40x+40y=140,
则5x+5y=17.5,
答:购买5支铅笔、5本笔记本共需17.5元.
【点睛】本题考查了二元一次方程组,找出方程组中各方程的关系以及整体思想是解题的关键.
21.(1)水流速度是每小时5千米;
(2)救生圈从A港口漂流到B港口所需时间为48小时;
(3)救生圈于上午12时掉入水中.
【分析】本题主要考查二元一次方程组的应用,解题的关键是理解题意;
(1)设小船在静水中的速度为x千米/小时,水流速度为y千米/小时,然后根据题意可列方程组为,可进行求解;
(2)设小船在静水中的速度为a千米/小时,水流速度为b千米/小时,A港口到B港口的距离为s千米,然后根据题意可列方程为,然后根据行船问题可进行求解;
(3)设救生圈在出发小时掉入水中,小船需8小时到B港口,则救生圈从掉入水中到被找到共在水中漂流了小时,然后根据题意可列方程为,进而问题可求解.
【详解】(1)解:设小船在静水中的速度为x千米/小时,水流速度为y千米/小时,
由题意得:
,
解得:,
答:水流速度是每小时5千米;
(2)解:设小船在静水中的速度为a千米/小时,水流速度为b千米/小时,A港口到B港口的距离为s千米,由题意得:
,
解得:,
∴救生圈按水流速度由A港口漂流到B港口需要的时间为(小时);
答:救生圈从A港口漂流到B港口所需时间为48小时;
(3)解:设救生圈在出发小时掉入水中,小船需8小时到B港口,则救生圈从掉入水中到被找到共在水中漂流了小时,由题意得:
,
解得:,
∴;
答:救生圈于上午12时掉入水中.
22.(1)购进A型服装45件,购进B型服装30件
(2)服装店比按标价出售少收入1410元
【分析】(1)设购进A型服装x件,B型服装y件,根据“某服装店用5700元购进A,B两种新式服装,按标价售出后可获得毛利润3600元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)利用少收入的钱数=每件A型服装少挣的钱数×销售数量+每件B型服装少挣的钱数×销售数量,即可求出结论.
【详解】(1)设购进A种服装x件,购进B种服装y件,
根据题意得:,
解得:
答:购进A型服装45件,购进B型服装30件;
(2)
=450+960
(元).
答:服装店比按标价出售少收入1410元.
【点睛】本题考查了二元一次方程组的应用以及有理数的混合运算,找准等量关系,正确列出二元一次方程组是解题的关键.
23.(1)每辆型汽车的进价为20万元,每辆型汽车的进价为45万元;
(2)共两种购买方案,方案如下.方案一:购进型汽车11辆,型汽车4辆;方案二:购进型汽车2辆,型汽车8辆.
【分析】本题考查二元一次方程组的应用以及二元一次方程的应用,解题的关键是找准等量关系,正确列出二元一次方程(组).
(1)设每辆型汽车的进价为万元,每辆型汽车的进价为万元,根据题意列二元一次方程组,即可求解;
(2)设购买A型号的汽车m辆,B种型号的汽车n辆,根据总价为400万元列出二元一次方程,进而分析得出购买方案.
【详解】(1)设每辆型汽车的进价为万元,每辆型汽车的进价为万元.
依题意,得
解得
答:每辆型汽车的进价为20万元,每辆型汽车的进价为45万元;
(2)设购进型汽车辆,型汽车辆.
依题意,得,所以.
因为,均为正整数,
所以或
所以共两种购买方案,方案如下.
方案一:购进型汽车11辆,型汽车4辆.
方案二:购进型汽车2辆,型汽车8辆.
24.1个部件的质量为1.2吨,1个部件的质量为2吨
【分析】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
设1个部件的质量为吨,1个部件的质量为吨,根据3个部件和2个部件的总质量为7.6吨,5个部件和3个部件的质量相等.列出二元一次方程组,解方程组即可.
【详解】解:设1个部件的质量为吨,1个部件的质量为吨,
由题意得:,
解得:,
答:1个部件的质量为1.2吨,1个部件的质量为2吨.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.3二元一次方程组的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.为打造成渝地区双城经济圈,成渝高速公路在今年开始打造八车道高速公路通道,其中重庆段从重庆江北区到荣昌区全长约为,若一辆小汽车,一辆货车同时从江北,荣昌两地同时相向开出,经过45分钟相遇,相遇时小汽车比货车多行,设小汽车和货车的速度分别为,,则下列方程组正确的是( )
A. B. C. D.
2.若一个两位数,它的个位上的数字与十位上的数字和为5,则这样的两位数有( )
A.3个 B.4个 C.5个 D.6个
3.某公司有新员工和老员工若干名.已知1名新员工每天制造的零件个数比1名老员工少30,1名新员工与2名老员工每天共可制造180个零件,则1名新员工与1名老员工每天各能制造多少个零件?设1名新员工每天能制造个零件,1名老员工每天能制造个零件.根据题意可列方程组为()
A. B. C. D.
4.植树节这天有20名同学共种了52棵树苗,其中男生每人种树3棵,女生每人种树2棵设男生有人,女生有人,根据题意,下列方程组正确的是( )
A. B. C. D.
5.甲和乙两人玩“打弹珠”游戏,甲对乙说:“把你一半的弹珠给我,我就有35颗弹珠.”乙说:“把你弹珠的给我,我就有40颗弹珠.”若设乙有颗弹珠,甲有颗弹珠,则可列方程组为( )
A. B. C. D.
6.客车和货车分别在两条平行的铁轨上行驶,客车长米,货车长米如果两车相向而行,那么从两车车头相遇到车尾离开共需秒钟;如果客车从后面追货车,那么从客车车头追上货车车尾到客车车尾离开货车车头共需分秒,假设客车和货车每秒钟分别行驶和米,则可列方程组为( )
A. B.
C. D.
7.第二届杭州市月季花展于2024年4月27日在杭州开展,若黄色月季花每支4元,红色月季花每支6元,小明想要花费30元全部用于购买这两个品种的花送给妈妈,那么小明的购买方案有( )
A.1种 B.2种 C.3种 D.4种
8.一个两位数,十位数字比个位数字的2倍大1.若这个两位数减去36恰好等于个位数字与十位数字对调后所得的两位数,则这个两位数是( )
A.86 B.68 C.94 D.73
9.某班的一个综合实践活动小组去甲、乙两个超市调查去年和今年“元旦”期间的销售情况,下面是调查后小明与其他两位同学进行交流的对话.
小明说:“去年两超市的销售额共为150万元,今年两超市的销售额共为170万元.”
小亮说:“甲超市的销售额今年比去年增加.”
小颖说:“乙超市的销售额今年比去年增加.”
根据他们的对话,得出今年甲超市的销售额为( )万元.
A.100 B.50 C.60 D.110
10.文峰超市以同样的价格卖出同样的牙刷和牙膏,以下是4天的记录:第1天,卖出13支牙刷和7盒牙膏,收入144元;第2天,卖出18支牙刷和11盒牙膏,收入219元;第3天,卖出23支牙刷和20盒牙膏,收入368元;第4天,卖出17支牙刷和11盒牙膏,收入216元.已知第1天和第2天的记录无误,第3天和第4天有一天的记录有误,则记录有误的一天收入( )
A.多记1元 B.多记2元 C.少记1元 D.少记2元
11.如图,宽为的矩形图案是由10个形状和大小完全一样的小长方形拼成,则一个小长方形的面积为( )
A. B. C. D.
12.爸爸骑摩托车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下:
时刻 9:00 10:00 11:30
里程碑上的数 是一个两位数,它的两个数字之和是6 是一个两位数,它的十位与个位数字与9:00所看到的正好互换了 是一个三位数,它比9:00时看到的两位数中间多了个0
则10:00时看到里程碑上的数是( )
A.15 B.24 C.42 D.51
二、填空题
13.某市为进一步加快文明城市的建设,园林局尝试种植A、B两种树种.经过试种后发现,种植A种树苗a棵,种下后成活了棵,种植B种树苗b棵,种下后成活了(b-2)棵.第一阶段两种树苗共种植40棵,且两种树苗的成活棵树相同,则种植A种树苗 棵.第二阶段,该园林局又种植A种树苗m棵,B种树苗n棵,若m=2n,在第一阶段的基础上进行统计,则这两个阶段种植A种树苗成活棵数 种植B种树苗成活棵数(填“>”“<”或“=”).
14.我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足.问鸡兔各几何.”设有只鸡,只兔,根据题意,可列方程组为 .
15.某工厂去年的总产值比总支出多500万元,而今年计划的总产值比总支出多950万元,已知今年计划总产值比去年增加15%,而计划总支出比去年减少10%,求去年计划的总产值和总支出各是多少万元?解:设去年计划的总产值、总支出分别是x万元、y万元,根据题意,可列方程组 .
16.中国古代数学著作《九章算术》中记载了这样一个题目:今有共买琎,人出半,盈四;人出少半,不足三.问人数,琎价各几何.其大意是今有人合伙买琎石,每人出钱,会多出4钱;每人出钱,又差了3钱.问人数,琎价各是多少.设人数为,琎价为,则可列方程组为 .
17.如图,在大长方形中不重叠的放入七个长、宽都相同的小长方形,根据图中给出的数据,可得出阴影部分面积为 .
三、解答题
18.如图,某校劳动小组计划利用已有的一堵长为6m的墙,用篱笆围成一个面积为的矩形劳动基地ABCD,边AD的长不超过墙的长度,在BC边上开设宽为1m的门EF(门不需要消耗篱笆).设AB的长为x(m),BC的长为y(m).
(1)若围成矩形劳动基地ABCD三边的篱笆总长为10m,求AB和BC的长度.
(2)若AB和BC的长都是整数(单位:m),且围成矩形劳动基地ABCD三边的篱笆总长小于10m,请直接写出所有满足条件的围建方案.
19.用10块相同的长方形地砖拼成一块矩形地面,地砖的拼放方式及相关数据如图所示.
(1)求每块地砖的长与宽.
(2)求所拼成的矩形地面的周长.
20.阅读感悟:
已知实数x,y满足3x-y=5①,2x+3y=7②,求x-4y和7x+5y的值.
本题常规思路是将①②两式联立组成方程组,解得x,y的值再代入欲求值的式子中得到答案,常规思路运算量比较大.其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得式子的值,如由①-②可得x-4y=-2,由①+②×2可得7x+5y= 19.这样的解题思路就利用了通常所说的“整体思想”.
[解决问题]已知二元一次方程组,则x-y= ,x+y= .
[拓展延伸]某班级组织活动需购买小奖品,买18支铅笔、27本笔记本共需86.4元,买22支铅笔、13本笔记本共需53.6元,则购买5支铅笔、5本笔记本共需多少元?
21.一只小船从港口顺水航行到港口需8小时,而从港口逆水返回到港口需12小时.某日,该小船在早晨8点出发,由港口顺水航行到港口时,发现船上一个救生圈在途中掉入水中,于是立即返回寻找救生圈,4小时后找到救生圈.
(1)若港口到港口的航程为240千米,求水流速度是每小时多少千米?
(2)若救生圈从港口漂流到港口,需要多长时间?
(3)救生圈于何时掉入水中?
22.某服装店用5700元购进A,B两种新式服装,按标价售出后可获得毛利润3600元(毛利润=售价-进价),这两种服装的进价,标价如表所示.
类型价格 A型 B型
进价(元/件) 60 100
标价(元/件) 100 160
(1)请利用二元一次方程组求这两种服装各购进的件数;
(2)如果A种服装按标价的9折出售,B种服装按标价的8折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?
23.随着“低碳生活,绿色出行”理念的普及,某汽车销售公司计划购进一批新能源汽车进行销售.据了解,1辆A型汽车、2辆B型汽车的进价共计110万元;2辆A型汽车、3辆B型汽车的进价共计175万元.
(1)每辆A,B两种型号的汽车进价分别为多少万元?
(2)若该公司计划正好用400万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),则该公司有哪几套方案?
24.现有一辆卡车,要运输若干套某种设备,每套设备由A部件和部件组成.已知3个A部件和2个部件的总质量为7.6吨,5个A部件和3个部件的质量相等.求1个A部件和1个部件的质量各是多少.
《6.3二元一次方程组的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C A D A A B D D C
题号 11 12
答案 A D
1.D
【分析】设小汽车和货车的速度分别为,,根据“全长约为,经过45分钟相遇,相遇时小汽车比货车多行”列方程组即可.
【详解】解:设小汽车和货车的速度分别为,,
45分钟小时,
由题意得:,
故选:D.
【点睛】本题考查了二元一次方程组的应用,找出合适的等量关系列出方程组是解题的关键.
2.C
【分析】根据题意列举出符合条件的数字即可解得.
【详解】解:一个两位数,个位上的数字和十位上的数字合起来是5,这样的两位数有:50,14,41,23,32.
故选:C.
3.A
【分析】本题二元一次方程组的应用,解题的关键是能够根据题意找到两个等量关系,这是列方程的依据.
找到两个等量关系列出方程组即可.
【详解】解:设一个生手工每天能制作x个零件,一个熟手工每天能制造y个零件,
根据题意得:,
故选A.
4.D
【分析】设男生有x人,女生有y人,根据男女生人数为20,共种了52棵树苗,列出方程组成方程组即可.
【详解】解:设男生有x人,女生有y人,
根据题意可得:,
故选:D.
【点睛】本题考查二元一次方程组的实际运用,找出题目蕴含的数量关系是解决问题的关键.
5.A
【分析】本题考查了列二元一次方程组(根据实际问题列二元一次方程组),读懂题意,根据题中的等量关系正确列出方程组是解题的关键.
根据题意即可直接得出答案.
【详解】解:由题意,可列方程组为:
,
故选:.
6.A
【分析】根据题意和题目中的数据,可知,,然后即可列出相应的方程组,本题得以解决.
【详解】解:分秒秒,
由题意可得,
,
故选:A.
【点睛】本题考查由实际问题抽象出二元一次方程组,解答本题的关键是明确题意,列出相应的方程组.
7.B
【分析】本题主要考查了二元一次方程的应用,解题的关键是根据题意列出方程.设黄色月季花x支,红色月季花y支,根据两种花的花费总共为30元,列出方程,解方程即可.
【详解】解:设黄色月季花x支,红色月季花y支,根据题意得:
,
∵x、y为正整数,
∴,,
∴小明的购买方案有2种,
故选:B.
8.D
【分析】本题考查二元一次方程组的实际应用,设十位数字是,个位数字是,由题意列方程组求解即可得到答案,读懂题意,准确列出二元一次方程组是解决问题的关键.
【详解】解:设十位数字是,个位数字是,
则,
解得,
原来的两位数是,
故选:D.
9.D
【分析】设甲超市去年销售额为x万元,乙超市去年销售额为y万元,根据题意列出方程组求解后,再求出甲超市今年的销售额即可.
【详解】解:设甲超市去年销售额为x万元,乙超市去年销售额为y万元,
根据题意,得:
,,
,
解得:,
所以今年甲超市销售额为.
故选:D.
【点睛】本题考查了二元一次方程组的应用,解决本题的关键是根据题意找到等量关系.
10.C
【解析】略
11.A
【分析】本题主要考查了二元一次方程组的实际应用,根据题意找到等量关系列出方程组是解题的关键.设小长方形的宽为,长为,再根据题意列方程组求得、,最后求面积即可.
【详解】解:设小长方形的宽为,长为,
根据题意得, ,
解得,
一个小长方形的面积为.
故选:A.
12.D
【分析】解:设小明9:00看到的两位数,十位数为x,个位数为y,根据车的速度不变和12:00时看到的两位数字之和为6,即可列出二元一次方程组,解方程组即可求解.
【详解】解:设小明9:00看到的两位数,十位数为x,个位数为y,由题意列方程组得:,
解得:,
∴9:00时看到的两位数是15.
10:00时看到里程碑上的数是
故选:D
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题关键.
13. 22 >
【详解】解:第一阶段,依题意得:,
解得:,
则种植A种树苗22棵;
第二阶段,∵种植A种树苗m棵,B种树苗n棵,若m=2n,
∴A种树苗成活了 n+5(棵),
B种树苗成活了n-2(棵),
∴这两个阶段A种树苗共成活了×22+5+ n+5= n+21(棵),
B种树苗共成活了18-2+ n-2= n+14(棵),
∵n+21> n+14,
∴这两个阶段A种树苗共成活棵数>B种树苗共成活棵数,
故答案为:>.
【点睛】本题考查了二元一次方程组的应用,列代数式,整式的加减运算,找准等量关系,正确列出二元一次方程组是解题的关键.
14.
【分析】根据“鸡的数量兔的数量,鸡的脚的数量兔子的脚的数量”可列方程组.
【详解】解:根据题意可得:,
故答案为:.
【点睛】本题考查由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,找出等量关系,列出相应的方程组.
15.
【分析】设去年计划的总产值是x万元,总支出y万元.根据“去年的总产值比总支出多500万元.由于今年总产值比去年增加15%,总支出比去年节约10%,因此,今年总产值比总支出多950万元”列方程组.
【详解】解:设去年计划的总产值是x万元,总支出y万元.根据题意,得
,
故答案为:.
【点睛】考查了二元一次方程组的应用,根据实际问题中的条件列方程时,要注意抓住题目中的一些关键性词语,找出等量关系,列出方程.
16.
【分析】本题考查了二元一次方程组的应用(古代问题),读懂题意,根据题中的等量关系正确列出方程组是解题的关键.
根据题意即可直接得出答案.
【详解】解:由题意,可列方程组为:
,
故答案为:.
17.
【分析】设小长方形的长为a,宽为b,观察图形,根据各边之间的关系,可得出关于a,b的二元一次方程组,解之可求出a,b的值,再利用阴影部分的面积=大长方形的面积-7×小长方形的面积,即可求出结论.
【详解】设小长方形的长为a,宽为b,
根据题意得:,
解得:,
∴阴影部分面积为:,
故答案为:.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
18.(1)AB=4,BC=3
(2)AB=2,BC=6或AB=3,BC=4
【分析】(1)根据;篱笆总长和门的长表示出AB、BC,列出方程即可.
(2)根据围成矩形三边的篱笆总长小于10列出不等式,再由x和y为整数且xy=12确定出满足题意的方案.
【详解】(1)根据题意得:,即.
代入得:,整理得:.
解得:或.
当时,,不符合题意;当时,,符合题意.
则AB=4,BC=3.
(2)根据题意得:,即.
∵AB,BC为整数,即x,y为整数,且.
∴当y=6时,x=2;当y=4时,x=3.
则满足条件的围建方案为:AB=2,BC=6或AB=3,BC=4.
【点睛】本题考查了一元二次方程的应用,弄清题意是解题的关键.
19.(1)每块地砖的长与宽分别为和
(2)所拼成的矩形地面的周长是
【分析】本题考查了二元一次方程组的应用,通过理解题意和观察图示可知本题存在两个等量关系是解题的关键.
(1)设每块地砖的长与宽分别为,根据图中关系可得,解方程组即可;
(2)由矩形周长公式求解.
【详解】(1)解:设每块地砖的长与宽分别为,
由题意得:,
解得:,
∴每块地砖的长与宽分别为和;
(2)解:所拼成的矩形地面的周长,
答:所拼成的矩形地面的周长是.
20.2;4;购买5支铅笔、5本笔记本共需17.5元
【分析】[解决问题]分别② ①,①+②即可求得;
[拓展延伸]设每只铅笔x元,每本笔记本y元,根据题意列出方程组,然后求得5(x+y)的值即可.
【详解】解:[解决问题],
② ①,得2x 2y=2,
即x y=4;
①+②,得4x+4y=16,
即x+y=4,
故答案为:2,4.
[拓展延伸]设每只铅笔x元,每本笔记本y元,
根据题意,得,
①+②,得40x+40y=140,
则5x+5y=17.5,
答:购买5支铅笔、5本笔记本共需17.5元.
【点睛】本题考查了二元一次方程组,找出方程组中各方程的关系以及整体思想是解题的关键.
21.(1)水流速度是每小时5千米;
(2)救生圈从A港口漂流到B港口所需时间为48小时;
(3)救生圈于上午12时掉入水中.
【分析】本题主要考查二元一次方程组的应用,解题的关键是理解题意;
(1)设小船在静水中的速度为x千米/小时,水流速度为y千米/小时,然后根据题意可列方程组为,可进行求解;
(2)设小船在静水中的速度为a千米/小时,水流速度为b千米/小时,A港口到B港口的距离为s千米,然后根据题意可列方程为,然后根据行船问题可进行求解;
(3)设救生圈在出发小时掉入水中,小船需8小时到B港口,则救生圈从掉入水中到被找到共在水中漂流了小时,然后根据题意可列方程为,进而问题可求解.
【详解】(1)解:设小船在静水中的速度为x千米/小时,水流速度为y千米/小时,
由题意得:
,
解得:,
答:水流速度是每小时5千米;
(2)解:设小船在静水中的速度为a千米/小时,水流速度为b千米/小时,A港口到B港口的距离为s千米,由题意得:
,
解得:,
∴救生圈按水流速度由A港口漂流到B港口需要的时间为(小时);
答:救生圈从A港口漂流到B港口所需时间为48小时;
(3)解:设救生圈在出发小时掉入水中,小船需8小时到B港口,则救生圈从掉入水中到被找到共在水中漂流了小时,由题意得:
,
解得:,
∴;
答:救生圈于上午12时掉入水中.
22.(1)购进A型服装45件,购进B型服装30件
(2)服装店比按标价出售少收入1410元
【分析】(1)设购进A型服装x件,B型服装y件,根据“某服装店用5700元购进A,B两种新式服装,按标价售出后可获得毛利润3600元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)利用少收入的钱数=每件A型服装少挣的钱数×销售数量+每件B型服装少挣的钱数×销售数量,即可求出结论.
【详解】(1)设购进A种服装x件,购进B种服装y件,
根据题意得:,
解得:
答:购进A型服装45件,购进B型服装30件;
(2)
=450+960
(元).
答:服装店比按标价出售少收入1410元.
【点睛】本题考查了二元一次方程组的应用以及有理数的混合运算,找准等量关系,正确列出二元一次方程组是解题的关键.
23.(1)每辆型汽车的进价为20万元,每辆型汽车的进价为45万元;
(2)共两种购买方案,方案如下.方案一:购进型汽车11辆,型汽车4辆;方案二:购进型汽车2辆,型汽车8辆.
【分析】本题考查二元一次方程组的应用以及二元一次方程的应用,解题的关键是找准等量关系,正确列出二元一次方程(组).
(1)设每辆型汽车的进价为万元,每辆型汽车的进价为万元,根据题意列二元一次方程组,即可求解;
(2)设购买A型号的汽车m辆,B种型号的汽车n辆,根据总价为400万元列出二元一次方程,进而分析得出购买方案.
【详解】(1)设每辆型汽车的进价为万元,每辆型汽车的进价为万元.
依题意,得
解得
答:每辆型汽车的进价为20万元,每辆型汽车的进价为45万元;
(2)设购进型汽车辆,型汽车辆.
依题意,得,所以.
因为,均为正整数,
所以或
所以共两种购买方案,方案如下.
方案一:购进型汽车11辆,型汽车4辆.
方案二:购进型汽车2辆,型汽车8辆.
24.1个部件的质量为1.2吨,1个部件的质量为2吨
【分析】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
设1个部件的质量为吨,1个部件的质量为吨,根据3个部件和2个部件的总质量为7.6吨,5个部件和3个部件的质量相等.列出二元一次方程组,解方程组即可.
【详解】解:设1个部件的质量为吨,1个部件的质量为吨,
由题意得:,
解得:,
答:1个部件的质量为1.2吨,1个部件的质量为2吨.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
