5.2 角 同步练习(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
5.2角
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图AB,交于点O,,,平分,则下列结论:①图中的余角有四个;②∠AOF的补角有2个;③为的平分线;④.其中结论正确的序号是( )
A.①②④ B.①③④ C.①④ D.②③④
2.下列说法中,正确的是( )
A.射线和射线是同一条射线
B.如果,那么是线段的中点
C.如果两个角互补,那么它们的角平分线所在直线的夹角为
D.如果两个角是同一个角的补角,那么它们相等
3.如图,已知点O在直线上,平分,平分,则的度数为( )
A. B. C. D.无法确定
4.如图,点在直线上,、分别平分、,则图中互为余角的有( )对
A.1 B.2 C.3 D.4
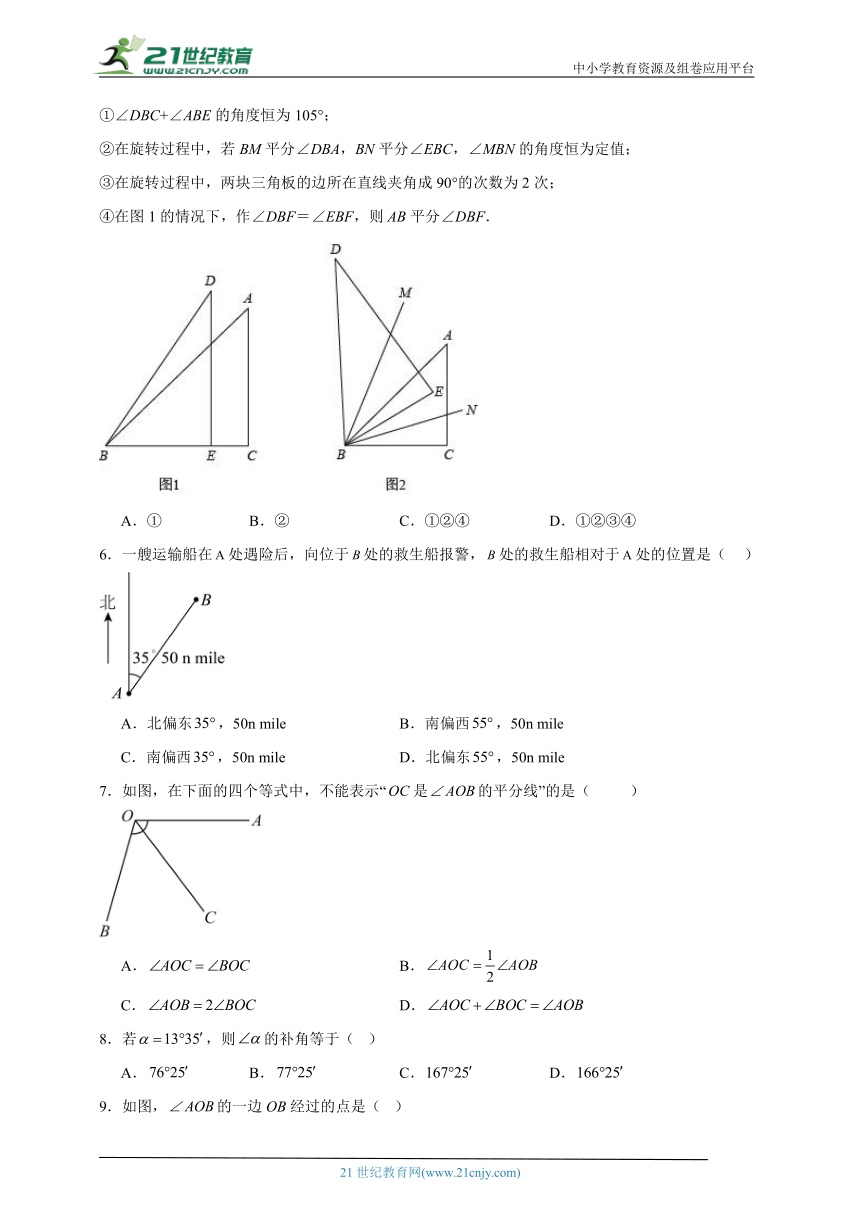
5.一副三角板ABC、DBE,如图1放置,(∠D=30°、∠BAC=45°),将三角板DBE绕点B逆时针旋转一定角度,如图2所示,且0°<∠CBE<90°,则下列结论中正确的是( )
①∠DBC+∠ABE的角度恒为105°;
②在旋转过程中,若BM平分∠DBA,BN平分∠EBC,∠MBN的角度恒为定值;
③在旋转过程中,两块三角板的边所在直线夹角成90°的次数为2次;
④在图1的情况下,作∠DBF=∠EBF,则AB平分∠DBF.
A.① B.② C.①②④ D.①②③④
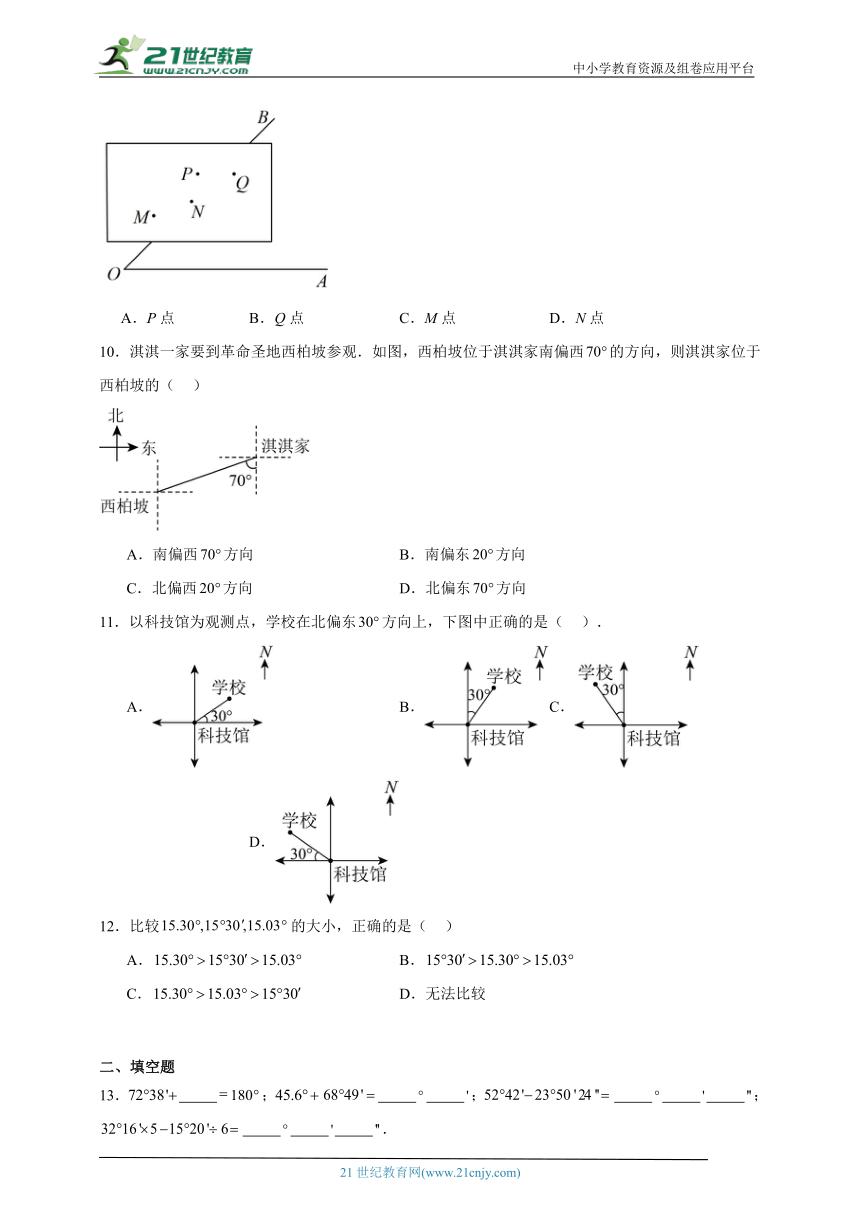
6.一艘运输船在处遇险后,向位于处的救生船报警,处的救生船相对于处的位置是( )
A.北偏东,50n mile B.南偏西,50n mile
C.南偏西,50n mile D.北偏东,50n mile
7.如图,在下面的四个等式中,不能表示“是的平分线”的是( )
A. B.
C. D.
8.若,则的补角等于( )
A. B. C. D.
9.如图,的一边OB经过的点是( )
A.P点 B.Q点 C.M点 D.N点
10.淇淇一家要到革命圣地西柏坡参观.如图,西柏坡位于淇淇家南偏西的方向,则淇淇家位于西柏坡的( )
A.南偏西方向 B.南偏东方向
C.北偏西方向 D.北偏东方向
11.以科技馆为观测点,学校在北偏东方向上,下图中正确的是( ).
A. B. C. D.
12.比较的大小,正确的是( )
A. B.
C. D.无法比较
二、填空题
13. ; ; ; .
14.如图,是的平分线,平分,且,则 .
15.已知与是对顶角,,则 ,的余角 .
16.如图,,垂足为O,射线在的内部,,若,平分,设,则 °(用含m的代数式表示).
17.角也可以由一条 线绕着它的端点旋转而成的图形.
三、解答题
18.已知、,求作:,使(保留作图痕迹).
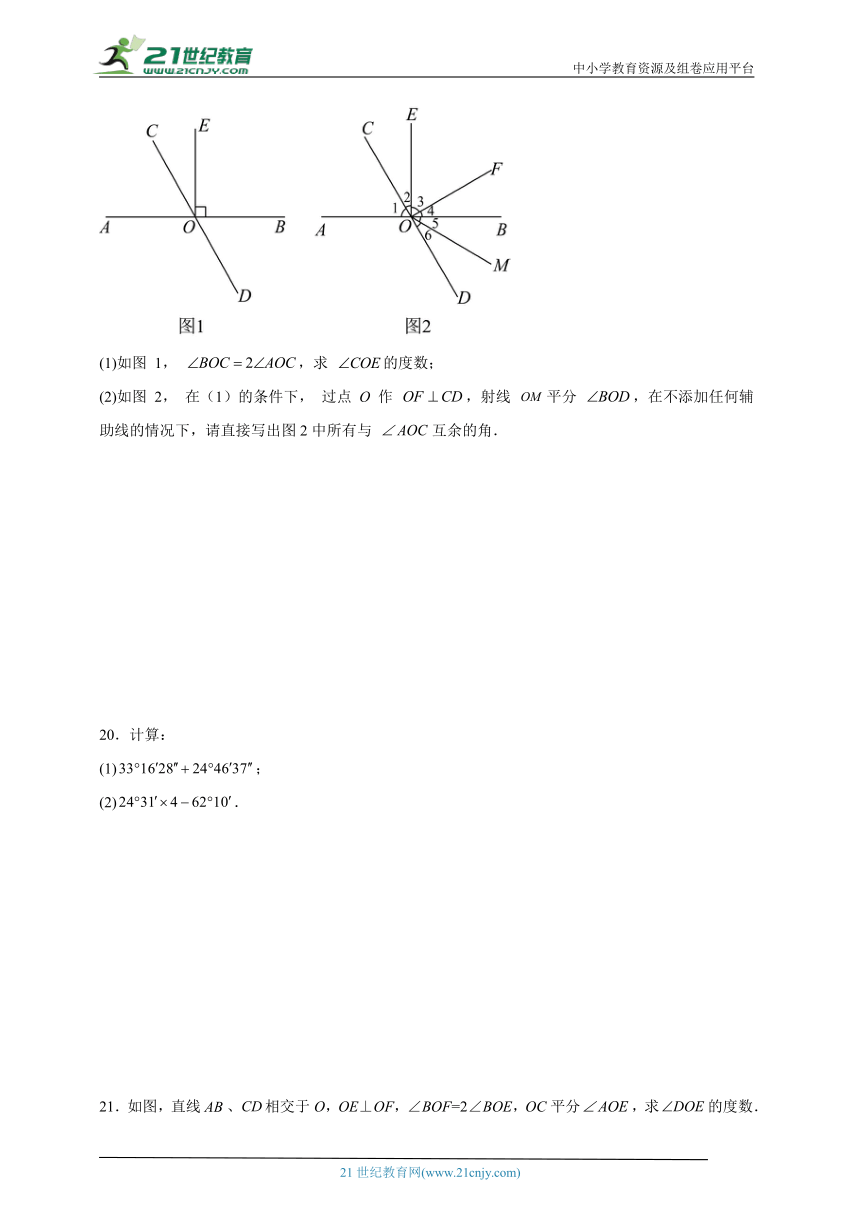
19.已知: 直线与直线交于点 O, 过点 O 作
(1)如图 1, ,求 的度数;
(2)如图 2, 在(1)的条件下, 过点 O 作 ,射线 平分 ,在不添加任何辅助线的情况下,请直接写出图2中所有与 互余的角.
20.计算:
(1);
(2).
21.如图,直线、相交于O,OE⊥OF,∠BOF=2∠BOE,OC平分,求的度数.
22.如图,,点A,B分别在射线,上,按下列要求画图,并回答问题.
(1)连接,过点O画线段的垂线,垂足为点D;
(2)画出的平分线,交于点E;
(3)在线段的延长线上取一点F,使得O是线段的中点;
(4)若,则 (用含x的代数式表示).
23.如图,是的角平分线,是的角平分线,是的角平分线,,求.
24.如图,已知,是的平分线,和互余,求的度数;
《5.2角》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A D B A D D D D
题号 11 12
答案 B B
1.C
【分析】①根据余角的定义可求解.②根据补角的定义可求解.③根据角平分线的定义无法证明.④根据对顶角及余角性质可求解.
【详解】①∵,
∴,
∵,
∴,
∵平分,
∴,
∵,
∴余角有,
故①正确.
②根据补角的定义可知的补角为,故②错误.
③∵不能证明,∴无法证明OD为∠EOG的平分线.
④根据对顶角以及余角的性质可知,
由①得,
∴,故④正确.
故选C.
【点睛】本题考查了余角、补角、对顶角以及角平分线的性质,注意结合图形,发现角与角之间的联系是解题关键.
2.D
【分析】根据射线、线段中点、补角、角平分线的定义和性质分析判断即可.
【详解】解:A. 射线和射线的端点不同,不是同一条射线,该说法错误,不符合题意;
B. 如果在同一直线上,,则是线段的中点,因为无法确定是否在同一直线,故该说法错误,不符合题意;
C. 如果相邻的两个角互补,那么它们的角平分线所在直线的夹角为,故该说法错误,不符合题意;
D. 如果两个角是同一个角的补角,那么它们相等,该说法正确,符合题意.
故选:D.
【点睛】本题主要考查了射线、线段中点、补角、角平分线的定义和性质等知识,熟练掌握相关知识是解题关键.
3.A
【分析】本题考查了角的计算和角平分线,解题的关键是掌握角的和差,角平分线的定义.
利用角平分线的定义进行解答即可.
【详解】解:∵平分,平分,
∴,
∴,
故选:A.
4.D
【分析】根据、分别平分、,可知;即可得出答案.
【详解】解:∵、分别平分、,
∴,;
∴
∴;
∴与互余,
与互余,
与互余,
与互余,
∴图中互为余角的有4对.
故选D
【点睛】本题考查角平分线的性质,互余的概念,角的相关计算等,熟练掌握角平分线平分角是解题的关键.
5.B
【分析】根据直角三角形两锐角互余、角平分线的定义、角的和差逐个判断即可得.
【详解】解:
如图1,当时
如图2,当时
因此,的角度不恒为,则①错误
如图1,当时
由角平分线的定义得
如图2,当时
由角平分线的定义得
因此,的角度恒为定值,则②正确
边与三角板的三边所在直线夹角不可能成
如图1,当时,设DE与AB的交点为F
,即
DE只与三角板的AB边所在直线夹角成,次数为1次;DB只与三角板的BC边所在直线夹角成,次数为1次
如图2,当时,延长DE交AB于点F
,即
只有DB与三角板的AB边所在直线夹角成,次数为1次
因此,在旋转过程中,两块三角板的边所在直线夹角成的次数为3次,则③错误
如图3,作
,即平分
如图4,作
显然不平分,则④错误
综上,正确的个数只有②这1个
故选:B.
【点睛】本题是一道较难的综合题,考查了直角三角形两锐角互余、角平分线的定义、角的和差等知识点,依据正确分两种情况讨论是解题关键.需注意的是,不能受两个示意图的影响,而少讨论一种情况.
6.A
【分析】根据方位角的概念以及确定位置的方法,可得答案.
【详解】解:由图知,遇险船B相对于救生船A的位置是北偏东,50n mile,
故选:A.
【点睛】本题考查了方向角的知识点,解答本题的关键是理解确定一个点的位置需要两个量:一个是方向角,一个是距离.
7.D
【分析】本题考查了角平分线的定义;根据角平分线的定义逐项判断即可.
【详解】解:A、,可得是的平分线,不符合题意;
B、,则,可得是的平分线,不符合题意;
C、,则,可得是的平分线,不符合题意;
D、,不能表示“是的平分线”, 符合题意;
故选:D.
8.D
【分析】本题考查了余角和补角,度分秒的换算,熟知互为补角的定义是解题的关键.如果两个角的和为,那么这两个角互为补角;由此计算即可.
【详解】解:若,
则的补角为,
故选:D.
9.D
【分析】组成角的两边是射线,射线的特点有:①只有一个端点;②直的;③向一边无线延伸.据此可用直尺去连接OB,看矩形内的哪个点在这条射线上即可.
【详解】解:画出射线可知,经过点.
故选:D.
【点睛】此题考查了角、射线的定义和画法,解题的关键是知道射线是直的.
10.D
【分析】根据方向角的定义可得答案.
【详解】解:如图:∵西柏坡位于淇淇家南偏西的方向,
∴淇淇家位于西柏坡的北偏东方向.
故选D.
【点睛】本题主要考查方向角,理解方向角的定义是正确解答的关键.
11.B
【分析】本题考查了方向角,熟练掌握方向角的定义是解题的关键.根据方向角的定义,即可解答.
【详解】解:以科技馆为观测点,学校在北偏东方向上,正确的是:
故选B
12.B
【分析】根据度分秒的换算方法,即,即可求解.
【详解】解:,,
∴,
故选:.
【点睛】本题主要考查角度的换算,掌握度分秒的换算方法是解题的关键.
13. 114 25 28 51 36 158 46 40
【分析】根据,逐个计算即可解答.注意:高级单位化为低级单位时,乘以60,反之,将低级单位转化为高级单位时除以60.同时,在进行度、分、秒的运算时也应注意借位和进位的方法.
【详解】解:
;
;
;
,
故答案为:;114;25;28;51;36;158;46;40.
【点睛】此题主要考查了度、分、秒的换算,此类题是进行度、分、秒的加、减、乘、除计算,注意以60为进制即可.
14./72度
【分析】本题考查角平分线,理解角平分线的概念是正确计算的前提.
根据角平分线的概念进行计算即可.
【详解】解:平分,,
,
又是的平分线,
,
故答案为:.
15.
【分析】本题考查了对顶角的性质,余角的定义,角度的换算,根据对顶角相等可得的度数,再根据余角的定义求出的余角,最后进行单位换算即可,掌握以上知识点是解题的关键.
【详解】解:∵与是对顶角,
∴,
∵,
∴的余角,
故答案为:,,.
16.2m或
【分析】分两种情况,由角平分线的定义,即可解决问题.
【详解】解:当在内时,如图(1),
∵平分,
∴,
∴,
∴;
当在外时,如图(2),
∵平分,
∴,
∴,
∴,
∴,
∴或.
故答案为:2m或.
【点睛】本题考查角的计算,角平分线定义,关键是要分两种情况讨论.
17.射
【解析】略
18.见解析
【分析】根据作一个角等于已知角的作法,先作,进而再的外部作,即可得到.
【详解】解:即为所求.
【点睛】本题考查了作图—复杂作图,解题关键是掌握作一个角等于已知角的尺规作图.
19.(1)
(2),,,
【分析】本题主要考查了几何图中角度的计算,求角的余角,角平分线的有关计算等知识.
(1)先利用平角的定义以及即可得出,进而可求出,由垂直的定义即可求出,最后根据角的和差关系即可得出答案.
(2)根据互余两角的和为90度一一计算即可得出答案.
【详解】(1)解:∵,
∴,
∴,
∴,
∵,
∴,
∴
(2)解:由(1)知,
∵,
∴和互余.
∵,
∴,,,
∴,
∴,
∴,
∵平分
∴,
∴,,,
则和互余,和互余,和互余,
综上:与互余的角有,,,.
20.(1)
(2)
【分析】(1)根据度分秒的进制,进行计算即可解答;
(2)根据度分秒的进制,进行计算即可解答.
【详解】(1)解:
(2)解:
【点睛】本题考查了度分秒的换算,熟练掌握度分秒的进制是解题的关键.
21.105°
【分析】根据垂直的定义可得∠EOF=90°,根据∠BOF=2∠BOE可得∠BOE=30°,根据平角的定义可得∠AOE=150°,根据角平分线的定义可得∠COE=75°,进而根据平角的定义可得答案.
【详解】∵OE⊥OF,
∴∠EOF=90°,
∵∠BOF=2∠BOE,∠BOE+∠BOF=∠EOF,
∴∠BOE=∠EOF=30°,
∴∠AOE=180°-∠BOE=150°,
∵OC平分,
∴∠COE=∠AOE=75°,
∴=180°-∠COE=105°.
【点睛】本题考查垂线的定义、平角的定义及角平分线的定义,熟练掌握定义是解题关键.
22.(1)见解析
(2)见解析
(3)见解析
(4)
【分析】(1)根据题意画出线段,用三角板过点O画线段的垂线即可;
(2)用量角器画出的平分线即可;
(3)在线段的延长线截取即可;
(4)根据角平分线定义得出,根据,得出,根据,求出即可.
【详解】(1)解:如图,即为所求;
(2)解:如图,即为所求;
(3)解:如图,点F即为所求;
(4)∵平分,
∴,
∵,
∴,
∵,
∴
.
【点睛】本题主要考查了作线段,垂线和角平分线,角平分线定义,解题的关键是数形结合,熟练掌握角平分线定义.
23.
【分析】本题考查的是角平分线的定义,角的和差倍分关系,能够根据定义正确表达出关系式是解决此题的关键.根据角平分线可得,,进而得出,即可求解.
【详解】解∶∵是的角平分线,
∴,
∵是的角平分线,是的角平分线,
∴,,
∴,
∴,
∴,
∴,
又,
∴.
24.
【分析】本题考查了余角和补角以及角平分线的定义,解答本题的关键是掌握互余两角之和为.先根据,是的平分线,求出的度数,然后根据互余两角之和为,求出的度数.
【详解】解:因为,是的平分线,
所以
因为和互余,
所以
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.2角
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图AB,交于点O,,,平分,则下列结论:①图中的余角有四个;②∠AOF的补角有2个;③为的平分线;④.其中结论正确的序号是( )
A.①②④ B.①③④ C.①④ D.②③④
2.下列说法中,正确的是( )
A.射线和射线是同一条射线
B.如果,那么是线段的中点
C.如果两个角互补,那么它们的角平分线所在直线的夹角为
D.如果两个角是同一个角的补角,那么它们相等
3.如图,已知点O在直线上,平分,平分,则的度数为( )
A. B. C. D.无法确定
4.如图,点在直线上,、分别平分、,则图中互为余角的有( )对
A.1 B.2 C.3 D.4
5.一副三角板ABC、DBE,如图1放置,(∠D=30°、∠BAC=45°),将三角板DBE绕点B逆时针旋转一定角度,如图2所示,且0°<∠CBE<90°,则下列结论中正确的是( )
①∠DBC+∠ABE的角度恒为105°;
②在旋转过程中,若BM平分∠DBA,BN平分∠EBC,∠MBN的角度恒为定值;
③在旋转过程中,两块三角板的边所在直线夹角成90°的次数为2次;
④在图1的情况下,作∠DBF=∠EBF,则AB平分∠DBF.
A.① B.② C.①②④ D.①②③④
6.一艘运输船在处遇险后,向位于处的救生船报警,处的救生船相对于处的位置是( )
A.北偏东,50n mile B.南偏西,50n mile
C.南偏西,50n mile D.北偏东,50n mile
7.如图,在下面的四个等式中,不能表示“是的平分线”的是( )
A. B.
C. D.
8.若,则的补角等于( )
A. B. C. D.
9.如图,的一边OB经过的点是( )
A.P点 B.Q点 C.M点 D.N点
10.淇淇一家要到革命圣地西柏坡参观.如图,西柏坡位于淇淇家南偏西的方向,则淇淇家位于西柏坡的( )
A.南偏西方向 B.南偏东方向
C.北偏西方向 D.北偏东方向
11.以科技馆为观测点,学校在北偏东方向上,下图中正确的是( ).
A. B. C. D.
12.比较的大小,正确的是( )
A. B.
C. D.无法比较
二、填空题
13. ; ; ; .
14.如图,是的平分线,平分,且,则 .
15.已知与是对顶角,,则 ,的余角 .
16.如图,,垂足为O,射线在的内部,,若,平分,设,则 °(用含m的代数式表示).
17.角也可以由一条 线绕着它的端点旋转而成的图形.
三、解答题
18.已知、,求作:,使(保留作图痕迹).
19.已知: 直线与直线交于点 O, 过点 O 作
(1)如图 1, ,求 的度数;
(2)如图 2, 在(1)的条件下, 过点 O 作 ,射线 平分 ,在不添加任何辅助线的情况下,请直接写出图2中所有与 互余的角.
20.计算:
(1);
(2).
21.如图,直线、相交于O,OE⊥OF,∠BOF=2∠BOE,OC平分,求的度数.
22.如图,,点A,B分别在射线,上,按下列要求画图,并回答问题.
(1)连接,过点O画线段的垂线,垂足为点D;
(2)画出的平分线,交于点E;
(3)在线段的延长线上取一点F,使得O是线段的中点;
(4)若,则 (用含x的代数式表示).
23.如图,是的角平分线,是的角平分线,是的角平分线,,求.
24.如图,已知,是的平分线,和互余,求的度数;
《5.2角》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A D B A D D D D
题号 11 12
答案 B B
1.C
【分析】①根据余角的定义可求解.②根据补角的定义可求解.③根据角平分线的定义无法证明.④根据对顶角及余角性质可求解.
【详解】①∵,
∴,
∵,
∴,
∵平分,
∴,
∵,
∴余角有,
故①正确.
②根据补角的定义可知的补角为,故②错误.
③∵不能证明,∴无法证明OD为∠EOG的平分线.
④根据对顶角以及余角的性质可知,
由①得,
∴,故④正确.
故选C.
【点睛】本题考查了余角、补角、对顶角以及角平分线的性质,注意结合图形,发现角与角之间的联系是解题关键.
2.D
【分析】根据射线、线段中点、补角、角平分线的定义和性质分析判断即可.
【详解】解:A. 射线和射线的端点不同,不是同一条射线,该说法错误,不符合题意;
B. 如果在同一直线上,,则是线段的中点,因为无法确定是否在同一直线,故该说法错误,不符合题意;
C. 如果相邻的两个角互补,那么它们的角平分线所在直线的夹角为,故该说法错误,不符合题意;
D. 如果两个角是同一个角的补角,那么它们相等,该说法正确,符合题意.
故选:D.
【点睛】本题主要考查了射线、线段中点、补角、角平分线的定义和性质等知识,熟练掌握相关知识是解题关键.
3.A
【分析】本题考查了角的计算和角平分线,解题的关键是掌握角的和差,角平分线的定义.
利用角平分线的定义进行解答即可.
【详解】解:∵平分,平分,
∴,
∴,
故选:A.
4.D
【分析】根据、分别平分、,可知;即可得出答案.
【详解】解:∵、分别平分、,
∴,;
∴
∴;
∴与互余,
与互余,
与互余,
与互余,
∴图中互为余角的有4对.
故选D
【点睛】本题考查角平分线的性质,互余的概念,角的相关计算等,熟练掌握角平分线平分角是解题的关键.
5.B
【分析】根据直角三角形两锐角互余、角平分线的定义、角的和差逐个判断即可得.
【详解】解:
如图1,当时
如图2,当时
因此,的角度不恒为,则①错误
如图1,当时
由角平分线的定义得
如图2,当时
由角平分线的定义得
因此,的角度恒为定值,则②正确
边与三角板的三边所在直线夹角不可能成
如图1,当时,设DE与AB的交点为F
,即
DE只与三角板的AB边所在直线夹角成,次数为1次;DB只与三角板的BC边所在直线夹角成,次数为1次
如图2,当时,延长DE交AB于点F
,即
只有DB与三角板的AB边所在直线夹角成,次数为1次
因此,在旋转过程中,两块三角板的边所在直线夹角成的次数为3次,则③错误
如图3,作
,即平分
如图4,作
显然不平分,则④错误
综上,正确的个数只有②这1个
故选:B.
【点睛】本题是一道较难的综合题,考查了直角三角形两锐角互余、角平分线的定义、角的和差等知识点,依据正确分两种情况讨论是解题关键.需注意的是,不能受两个示意图的影响,而少讨论一种情况.
6.A
【分析】根据方位角的概念以及确定位置的方法,可得答案.
【详解】解:由图知,遇险船B相对于救生船A的位置是北偏东,50n mile,
故选:A.
【点睛】本题考查了方向角的知识点,解答本题的关键是理解确定一个点的位置需要两个量:一个是方向角,一个是距离.
7.D
【分析】本题考查了角平分线的定义;根据角平分线的定义逐项判断即可.
【详解】解:A、,可得是的平分线,不符合题意;
B、,则,可得是的平分线,不符合题意;
C、,则,可得是的平分线,不符合题意;
D、,不能表示“是的平分线”, 符合题意;
故选:D.
8.D
【分析】本题考查了余角和补角,度分秒的换算,熟知互为补角的定义是解题的关键.如果两个角的和为,那么这两个角互为补角;由此计算即可.
【详解】解:若,
则的补角为,
故选:D.
9.D
【分析】组成角的两边是射线,射线的特点有:①只有一个端点;②直的;③向一边无线延伸.据此可用直尺去连接OB,看矩形内的哪个点在这条射线上即可.
【详解】解:画出射线可知,经过点.
故选:D.
【点睛】此题考查了角、射线的定义和画法,解题的关键是知道射线是直的.
10.D
【分析】根据方向角的定义可得答案.
【详解】解:如图:∵西柏坡位于淇淇家南偏西的方向,
∴淇淇家位于西柏坡的北偏东方向.
故选D.
【点睛】本题主要考查方向角,理解方向角的定义是正确解答的关键.
11.B
【分析】本题考查了方向角,熟练掌握方向角的定义是解题的关键.根据方向角的定义,即可解答.
【详解】解:以科技馆为观测点,学校在北偏东方向上,正确的是:
故选B
12.B
【分析】根据度分秒的换算方法,即,即可求解.
【详解】解:,,
∴,
故选:.
【点睛】本题主要考查角度的换算,掌握度分秒的换算方法是解题的关键.
13. 114 25 28 51 36 158 46 40
【分析】根据,逐个计算即可解答.注意:高级单位化为低级单位时,乘以60,反之,将低级单位转化为高级单位时除以60.同时,在进行度、分、秒的运算时也应注意借位和进位的方法.
【详解】解:
;
;
;
,
故答案为:;114;25;28;51;36;158;46;40.
【点睛】此题主要考查了度、分、秒的换算,此类题是进行度、分、秒的加、减、乘、除计算,注意以60为进制即可.
14./72度
【分析】本题考查角平分线,理解角平分线的概念是正确计算的前提.
根据角平分线的概念进行计算即可.
【详解】解:平分,,
,
又是的平分线,
,
故答案为:.
15.
【分析】本题考查了对顶角的性质,余角的定义,角度的换算,根据对顶角相等可得的度数,再根据余角的定义求出的余角,最后进行单位换算即可,掌握以上知识点是解题的关键.
【详解】解:∵与是对顶角,
∴,
∵,
∴的余角,
故答案为:,,.
16.2m或
【分析】分两种情况,由角平分线的定义,即可解决问题.
【详解】解:当在内时,如图(1),
∵平分,
∴,
∴,
∴;
当在外时,如图(2),
∵平分,
∴,
∴,
∴,
∴,
∴或.
故答案为:2m或.
【点睛】本题考查角的计算,角平分线定义,关键是要分两种情况讨论.
17.射
【解析】略
18.见解析
【分析】根据作一个角等于已知角的作法,先作,进而再的外部作,即可得到.
【详解】解:即为所求.
【点睛】本题考查了作图—复杂作图,解题关键是掌握作一个角等于已知角的尺规作图.
19.(1)
(2),,,
【分析】本题主要考查了几何图中角度的计算,求角的余角,角平分线的有关计算等知识.
(1)先利用平角的定义以及即可得出,进而可求出,由垂直的定义即可求出,最后根据角的和差关系即可得出答案.
(2)根据互余两角的和为90度一一计算即可得出答案.
【详解】(1)解:∵,
∴,
∴,
∴,
∵,
∴,
∴
(2)解:由(1)知,
∵,
∴和互余.
∵,
∴,,,
∴,
∴,
∴,
∵平分
∴,
∴,,,
则和互余,和互余,和互余,
综上:与互余的角有,,,.
20.(1)
(2)
【分析】(1)根据度分秒的进制,进行计算即可解答;
(2)根据度分秒的进制,进行计算即可解答.
【详解】(1)解:
(2)解:
【点睛】本题考查了度分秒的换算,熟练掌握度分秒的进制是解题的关键.
21.105°
【分析】根据垂直的定义可得∠EOF=90°,根据∠BOF=2∠BOE可得∠BOE=30°,根据平角的定义可得∠AOE=150°,根据角平分线的定义可得∠COE=75°,进而根据平角的定义可得答案.
【详解】∵OE⊥OF,
∴∠EOF=90°,
∵∠BOF=2∠BOE,∠BOE+∠BOF=∠EOF,
∴∠BOE=∠EOF=30°,
∴∠AOE=180°-∠BOE=150°,
∵OC平分,
∴∠COE=∠AOE=75°,
∴=180°-∠COE=105°.
【点睛】本题考查垂线的定义、平角的定义及角平分线的定义,熟练掌握定义是解题关键.
22.(1)见解析
(2)见解析
(3)见解析
(4)
【分析】(1)根据题意画出线段,用三角板过点O画线段的垂线即可;
(2)用量角器画出的平分线即可;
(3)在线段的延长线截取即可;
(4)根据角平分线定义得出,根据,得出,根据,求出即可.
【详解】(1)解:如图,即为所求;
(2)解:如图,即为所求;
(3)解:如图,点F即为所求;
(4)∵平分,
∴,
∵,
∴,
∵,
∴
.
【点睛】本题主要考查了作线段,垂线和角平分线,角平分线定义,解题的关键是数形结合,熟练掌握角平分线定义.
23.
【分析】本题考查的是角平分线的定义,角的和差倍分关系,能够根据定义正确表达出关系式是解决此题的关键.根据角平分线可得,,进而得出,即可求解.
【详解】解∶∵是的角平分线,
∴,
∵是的角平分线,是的角平分线,
∴,,
∴,
∴,
∴,
∴,
又,
∴.
24.
【分析】本题考查了余角和补角以及角平分线的定义,解答本题的关键是掌握互余两角之和为.先根据,是的平分线,求出的度数,然后根据互余两角之和为,求出的度数.
【详解】解:因为,是的平分线,
所以
因为和互余,
所以
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
