7.1 两条直线的位置关系 同步练习(含解析)
文档属性
| 名称 | 7.1 两条直线的位置关系 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 921.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-02 06:14:13 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
7.1两条直线的位置关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若,则的余角为( )
A. B. C. D.
2.已知 与 是对顶角,且,则 的度数为( )
A. B. C. D.
3.下列生活实例中,属于平行线的有( )
①交通路口的斑马线;②天上的彩虹;③体操的纵队所在直线;④百米跑道线;⑤火车的水平铁轨直线.
A.1个 B.2个 C.3个 D.4个
4.下列选项中,过点画的垂线,三角板放法正确的是( )
A. B.
C. D.
5.如图,C,D在线段上,下列四个说法:
①直线上以B,C,D,E为端点的线段共有6条;
②图中有3对互为补角的角;
③若,,则以A为顶点的所有小于平角的角的度数和为370°;
④若,,,点F是线段上任意一点(包含端点),则点F到点B,C,D,E的距离之和的最小值为15,最大值为25
其中正确说法的个数是( )
A.1个 B.2个 C.3个 D.4个
6.一个角的度数为,则这个角的余角和补角的度数分别为( ).
A., B.,
C., D.,
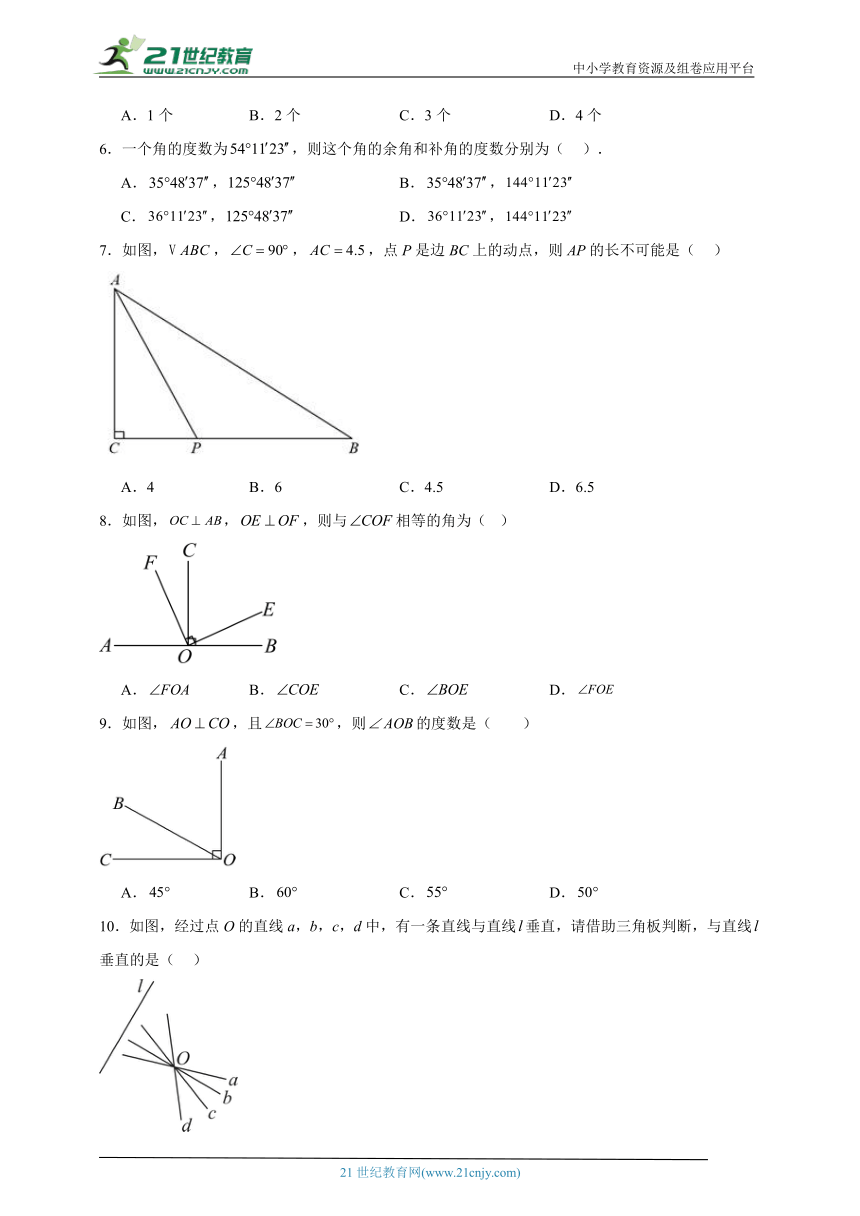
7.如图,,,,点P是边BC上的动点,则AP的长不可能是( )
A.4 B.6 C.4.5 D.6.5
8.如图,,,则与相等的角为( )
A. B. C. D.
9.如图,,且,则的度数是( )
A. B. C. D.
10.如图,经过点O的直线a,b,c,d中,有一条直线与直线垂直,请借助三角板判断,与直线垂直的是( )
A.直线a B.直线b C.直线c D.直线d
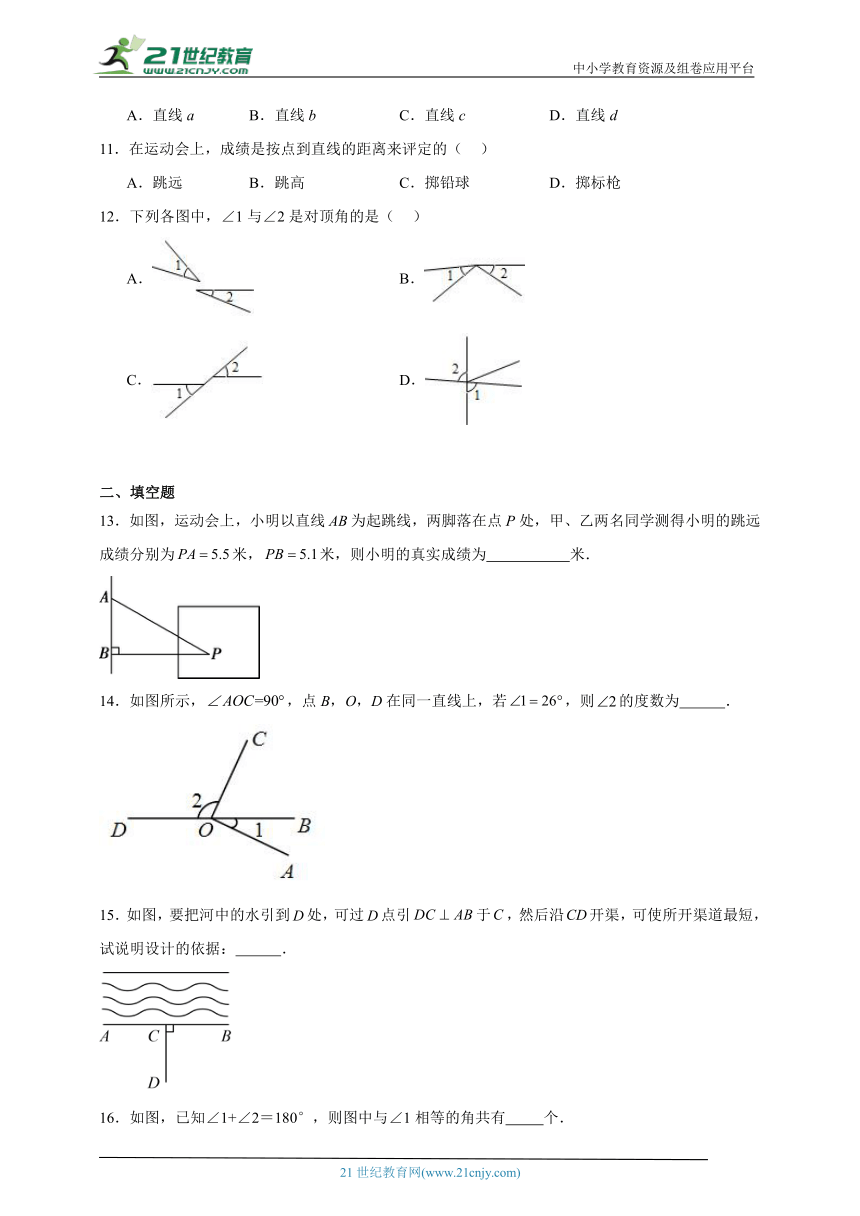
11.在运动会上,成绩是按点到直线的距离来评定的( )
A.跳远 B.跳高 C.掷铅球 D.掷标枪
12.下列各图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
二、填空题
13.如图,运动会上,小明以直线为起跳线,两脚落在点P处,甲、乙两名同学测得小明的跳远成绩分别为米,米,则小明的真实成绩为 米.
14.如图所示,,点B,O,D在同一直线上,若,则的度数为 .
15.如图,要把河中的水引到处,可过点引于,然后沿开渠,可使所开渠道最短,试说明设计的依据: .
16.如图,已知∠1+∠2=180°,则图中与∠1相等的角共有 个.
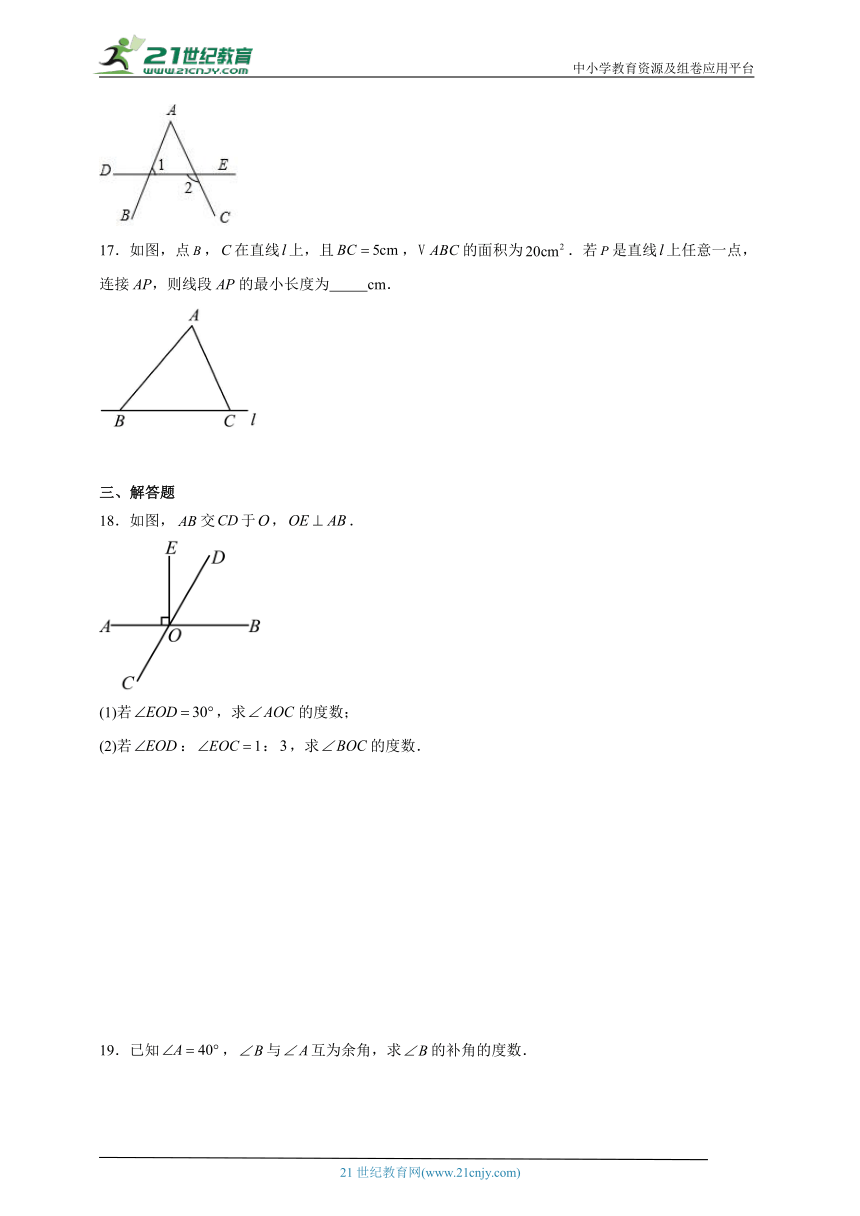
17.如图,点,在直线上,且,的面积为.若是直线上任意一点,连接AP,则线段AP的最小长度为 cm.
三、解答题
18.如图,交于,.
(1)若,求的度数;
(2)若::,求的度数.
19.已知,与互为余角,求的补角的度数.
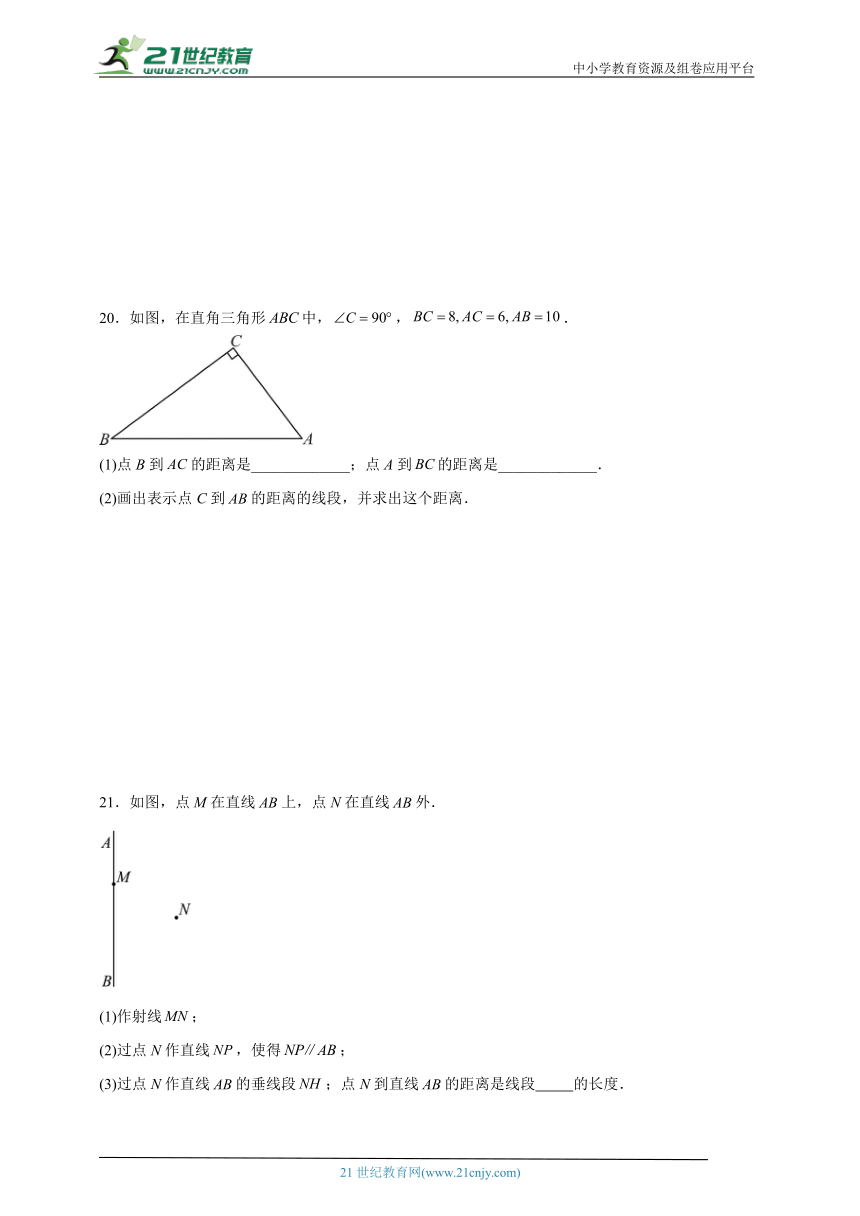
20.如图,在直角三角形中,,.
(1)点B到的距离是_____________;点A到的距离是_____________.
(2)画出表示点C到的距离的线段,并求出这个距离.
21.如图,点M在直线上,点N在直线外.
(1)作射线;
(2)过点N作直线,使得;
(3)过点N作直线的垂线段;点N到直线的距离是线段 的长度.
22.图,国道上有一出口,现要在附近公路旁建一个加油站.欲使加油站到出口的距离最短,请在公路上作出点的位置.
23.利用网格画图:
(1)过点C画的垂线,垂足为E;
(2)线段的长度是点C到直线_______的距离;
(3)连接,在线段中,线段_______最短.
24.如图(甲),和都是直角.
(1)如果,说出的度数.
(2)找出图(甲)中相等的角.如果,它们还会相等吗?
(3)若变小,如何变化?
(4)在图(乙)中利用能够画直角的工具再画一个与相等的角.
《3.1两条直线的位置关系》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C D C C A A C B B
题号 11 12
答案 A D
1.A
【分析】本题考查了求一个角的余角,掌握和为 的两角互为余角是解题的关键.
用减去即可求解.
【详解】解:由,则的余角为
故选:A.
2.C
【分析】根据对顶角相等,即,结合已知,即可求的度数.
【详解】解:∵ 与 是对顶角
∴,
∵,
∴,
故选:C.
【点睛】本题考查了对顶角相等,熟练掌握对顶角相等是解题的关键.
3.D
【分析】本题考查了平行线的定义:在同一平面内,不相交的两条直线叫平行线.根据在同一平面内,不相交的两条直线叫平行线即可确定.
【详解】根据平行线的定义可知①③④⑤是平行线,②天上的彩虹不是直线,故不是平行线,
所以属于平行线的有4个,
故选D.
4.C
【分析】本题主要考查了用三角板画垂线,解题的关键是熟练掌握用三角板画垂线的方法.根据画垂线的方法进行判断即可.
【详解】解:∵三角板有一个角是直角,
∴三角板的一条直角边与直线重合,
∵过点P作直线的垂线,
∴三角板的另一条直角边过点P,
∴符合上述条件的图形只有选项C.
故选:C.
5.C
【分析】①按照一定的顺序数出线段的条数即可;②图中互补的角就是分别以C、D为顶点的两对邻补角,由此即可确定选择项;③根据角的和与差计算即可;④分两种情况探讨:当F在线段上最小,点F和E重合最大计算得出答案即可.
【详解】解:①以B、C、D、E为端点的线段共6条,故①正确;
②图中互补的角就是分别以C、D为顶点的两对邻补角,即和互补,和互补,故②错误;
③由,根据图形可以求出
,故③正确;
④当F在线段上,则点F到点B,C,D,E的距离之和最小为,当F和E重合,则点F到点B、C、D、E的距离之和最大为,④正确.
故选:C.
【点睛】此题分别考查了线段、角的和与差以及补角的定义,解题时注意:互为邻补角的两个角的和为180°.
6.A
【分析】根据余角和补角的定义得出结果.
【详解】解:∵一个角的度数为54°11′23″,
∴这个角的余角的度数为:90°-54°11′23″=35°48′37″;
补角的度数为:180°-54°11′23″=125°48′37″.
故选:A.
【点睛】本题考查了余角与补角的定义,主要记住互为余角的两个角的和为90度,互为补角的两个角的和为180度,比较简单.
7.A
【分析】根据点到直线的距离,垂线段最短即可求解.
【详解】解:∵,,,
∴到的距离为4.5,
点P是边BC上的动点,则AP的长不可能是4.
故选A.
【点睛】本题考查了点到直线的距离,垂线段最短,理解到的距离为4.5是解题的关键.
8.C
【分析】本题主要考查余角和补角,由垂直的定义得出,即,根据余角的性质可得答案.
【详解】解:∵,,
∴,
∴,
∴.
故选:C.
9.B
【分析】根据垂直的定义,由,得.由,根据角的和差关系得到.
【详解】解:∵,
∴.
∵,
∴.
故选:B.
【点睛】本题考查了垂线,余角的知识.要注意领会由垂直得直角这一要点.
10.B
【分析】用三角板的两条直角边中的一条与直线L重合,再另一条边直角边能与a、b、c、d中的那条边重合即可得解.
【详解】解:用三角板的两条直角边中的一条与直线l重合,再另一条边直角边能与b重合,
故选:B.
【点睛】本题主要是考查了两条直线垂直的性质,两条直线垂直其所夹的角为直角.
11.A
【分析】点到直线的距离是指垂线段的长度,据此逐一分析即可得到答案.
【详解】解:点到直线的距离是指垂线段的长度,
只有跳远的成绩按此评定,
故选:A.
【点睛】本题考查了点到直线的距离,解题关键是掌握点到直线的距离即垂线段的长度.
12.D
【解析】略
13.
【分析】本题考查的是垂线段最短,熟知“垂线段最短”是解答此题的关键. 根据垂线段最短即可得出结论.
【详解】解:∵小明的真实成绩为点P到直线的距离,
∴小明的真实成绩为米,
故答案为:.
14.116°
【分析】由图示可得,∠1与∠BOC互余,结合已知可求∠BOC,又因为∠2与∠COB互补,即可求出∠2的度数.
【详解】解:∵,∠AOC=90°,
∴∠BOC=64°,
∵∠2+∠BOC=180°,
∴∠2=116°.
故答案为:116°.
【点睛】此题考查了余角和补角的知识,属于基础题,关键是掌握互余的两角之和为90°,互补的两角之和为180°.
15.垂线段最短
【分析】本题考查了垂线段最短,利用了垂线段的性质:直线外的点与直线上任意一点的连线中垂线段最短.根据垂线段的性质,可得答案.
【详解】解:要把池中的水引到处,可过点引于,然后沿开渠,可使所开渠道最短,试说明设计的依据:垂线段最短.
故答案为:垂线段最短.
16.3
【分析】根据补角的性质、对顶角的性质,可得答案.
【详解】解:如图
,
∵∠1和∠3是对顶角.
∴∠1=∠3.
∵∠1+∠2=180°,∠2+∠4=180°,∠2+∠5=180°,
∴∠1=∠4=∠5,
故答案为:3.
【点睛】本题考查了对顶角、邻补角,利用补角的性质、对顶角的性质是解题关键.
17.8
【分析】根据点到直线的垂线段最短,再由面积求出高,即为AP的最小值,由题知,过点A作BC的垂线,即为所求,此时,该垂线也是三角形的高.
【详解】解:过点A作BC的垂线AP,根据点到直线的所有线段中,垂线段最短,
∴垂线段即为AP的最小值,
∵BC=5cm,ΔABC的面积为20,
∴,
∴AP=8,
故答案为:8.
【点睛】本题考查三角形的面积公式,垂线段最短的性质,属于基础题.
18.(1)
(2)
【分析】利用垂直定义和对顶角的性质可得答案;
设,,利用邻补角互补可得方程,然后解出的值,进而可得的度数,再利用对顶角的性质可得答案.
【详解】(1)解:,
,
,
,
;
(2)设,,
,
解得:,
,
,
,
,
.
【点睛】此题主要考查了垂线,以及对顶角,关键是掌握对顶角相等,理清图中角之间的关系.
19.
【分析】本题考查了与余角、补角有关的计算,互余的两个角和为,互补的两个角和为,据此即可求解.
【详解】解∶∵与互为余角,
∴,
∵,
∴,
∴的补角的度数为.
20.(1)8; 6
(2)图见解析;点C到的距离是
【分析】本题考查了点到直线的距离,熟练掌握点到直线的距离的概念及等面积法是解题的关键,
(1)根据点到直线的距离的概念进行求解即可得到答案;
(2)过点作,则线段表示点C到的距离,再利用等面积法即可求得线段的长.
【详解】(1)解:∵三角形为直角三角形,,,
∵,
∴点B到的距离是的长度为8,
∵
∴点A到的距离是的长度为6.
故答案为:8;6.
(2)解:过点作,如图,线段即为所求.
,即,
,
∴点C到的距离是.
21.(1)作图见解析
(2)作图见解析
(3)作图见解析,
【分析】(1)作射线即可;
(2)过点N作直线,使得即可;
(3)过点N作直线的垂线段;进而可得点N到直线的距离.
【详解】(1)
如图,射线即为所求;
(2)如图,直线即为所求;
(3)如图,垂线段即为所求;
所以点N到直线的距离是线段的长度.
故答案为:.
【点睛】本题考查了作图﹣复杂作图,垂线,点到直线的距离,平行线的性质,解决本题的关键是掌握基本作图方法.
22.见解析
【分析】本题考查了垂线段的性质,熟练掌握垂线段最短是解题的关键.过点作,交于点,根据垂线段最短解答即可.
【详解】解:过点作,交于点,
如图所示,点即为所求.
23.(1)见详解
(2)
(3)
【分析】本题主要垂线及其做图,点到直线的距离概念,垂线段最短,注意作图的准确性.
(1)根据网格结构的特点,利用直线与网格的夹角的关系找出与垂直的格点;
(2)根据点到直线的距离概念回答;
(3)根据垂线段最短直接回答即可.
【详解】(1)解:如图所示:
(2)解:线段的长度是点C到直线的距离,
故答案为:;
(3)解:连接,在线段中,线段最短,
理由:垂线段最短.
故答案为:.
24.(1)的度数为;(2),,还会相等;(3)变大;(4)见解析.
【分析】(1)根据∠AOC=90°,∠DOC=28°,求出∠AOD的度数,然后即可求出∠AOB的度数;
(2)根据直角和等式的性质可得,∠AOD=∠BOC;
(3)根据∠AOD+∠DOC+∠DOC+∠BOC=180°,可得∠AOB+∠DOC=180°,进而得到∠DOC变小∠AOB变大,若∠DOC越来越大,则∠AOB越来越小.
(4)首先以OE为边,在∠EOF外画∠GOE=90°,再以OF为边在∠EOF外画∠HOF=90°,即可得到∠HOG=∠EOF.
【详解】解:(1)因为,∠AOC=∠DOB=90°,∠DOC=28°
所以,∠COB=90°﹣28°=62°,
所以,∠AOB=90°+62°=152°,
(2)相等的角有:∠AOC=∠DOB=90°,∠AOD=∠BOC;
因为∠AOD=∠AOC-∠DOC=∠DOB-∠DOC=∠COB
所以∠AOD=∠BOC;
如果∠DOC≠28°,他们还会相等;
(3)因为∠AOB=∠AOC+∠DOB-∠DOC=180°-∠DOC
所以当∠DOC越来越小,则∠AOB越来越大;
当∠DOC越来越大,则∠AOB越来越小
(4)如图,
画∠BOD=∠COE=90°,则∠BOC=∠DOH
即,∠DOH为所画的角.
【点睛】本题考查了余角和补角,以及角的计算,是基础题,准确识图是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
7.1两条直线的位置关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若,则的余角为( )
A. B. C. D.
2.已知 与 是对顶角,且,则 的度数为( )
A. B. C. D.
3.下列生活实例中,属于平行线的有( )
①交通路口的斑马线;②天上的彩虹;③体操的纵队所在直线;④百米跑道线;⑤火车的水平铁轨直线.
A.1个 B.2个 C.3个 D.4个
4.下列选项中,过点画的垂线,三角板放法正确的是( )
A. B.
C. D.
5.如图,C,D在线段上,下列四个说法:
①直线上以B,C,D,E为端点的线段共有6条;
②图中有3对互为补角的角;
③若,,则以A为顶点的所有小于平角的角的度数和为370°;
④若,,,点F是线段上任意一点(包含端点),则点F到点B,C,D,E的距离之和的最小值为15,最大值为25
其中正确说法的个数是( )
A.1个 B.2个 C.3个 D.4个
6.一个角的度数为,则这个角的余角和补角的度数分别为( ).
A., B.,
C., D.,
7.如图,,,,点P是边BC上的动点,则AP的长不可能是( )
A.4 B.6 C.4.5 D.6.5
8.如图,,,则与相等的角为( )
A. B. C. D.
9.如图,,且,则的度数是( )
A. B. C. D.
10.如图,经过点O的直线a,b,c,d中,有一条直线与直线垂直,请借助三角板判断,与直线垂直的是( )
A.直线a B.直线b C.直线c D.直线d
11.在运动会上,成绩是按点到直线的距离来评定的( )
A.跳远 B.跳高 C.掷铅球 D.掷标枪
12.下列各图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
二、填空题
13.如图,运动会上,小明以直线为起跳线,两脚落在点P处,甲、乙两名同学测得小明的跳远成绩分别为米,米,则小明的真实成绩为 米.
14.如图所示,,点B,O,D在同一直线上,若,则的度数为 .
15.如图,要把河中的水引到处,可过点引于,然后沿开渠,可使所开渠道最短,试说明设计的依据: .
16.如图,已知∠1+∠2=180°,则图中与∠1相等的角共有 个.
17.如图,点,在直线上,且,的面积为.若是直线上任意一点,连接AP,则线段AP的最小长度为 cm.
三、解答题
18.如图,交于,.
(1)若,求的度数;
(2)若::,求的度数.
19.已知,与互为余角,求的补角的度数.
20.如图,在直角三角形中,,.
(1)点B到的距离是_____________;点A到的距离是_____________.
(2)画出表示点C到的距离的线段,并求出这个距离.
21.如图,点M在直线上,点N在直线外.
(1)作射线;
(2)过点N作直线,使得;
(3)过点N作直线的垂线段;点N到直线的距离是线段 的长度.
22.图,国道上有一出口,现要在附近公路旁建一个加油站.欲使加油站到出口的距离最短,请在公路上作出点的位置.
23.利用网格画图:
(1)过点C画的垂线,垂足为E;
(2)线段的长度是点C到直线_______的距离;
(3)连接,在线段中,线段_______最短.
24.如图(甲),和都是直角.
(1)如果,说出的度数.
(2)找出图(甲)中相等的角.如果,它们还会相等吗?
(3)若变小,如何变化?
(4)在图(乙)中利用能够画直角的工具再画一个与相等的角.
《3.1两条直线的位置关系》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C D C C A A C B B
题号 11 12
答案 A D
1.A
【分析】本题考查了求一个角的余角,掌握和为 的两角互为余角是解题的关键.
用减去即可求解.
【详解】解:由,则的余角为
故选:A.
2.C
【分析】根据对顶角相等,即,结合已知,即可求的度数.
【详解】解:∵ 与 是对顶角
∴,
∵,
∴,
故选:C.
【点睛】本题考查了对顶角相等,熟练掌握对顶角相等是解题的关键.
3.D
【分析】本题考查了平行线的定义:在同一平面内,不相交的两条直线叫平行线.根据在同一平面内,不相交的两条直线叫平行线即可确定.
【详解】根据平行线的定义可知①③④⑤是平行线,②天上的彩虹不是直线,故不是平行线,
所以属于平行线的有4个,
故选D.
4.C
【分析】本题主要考查了用三角板画垂线,解题的关键是熟练掌握用三角板画垂线的方法.根据画垂线的方法进行判断即可.
【详解】解:∵三角板有一个角是直角,
∴三角板的一条直角边与直线重合,
∵过点P作直线的垂线,
∴三角板的另一条直角边过点P,
∴符合上述条件的图形只有选项C.
故选:C.
5.C
【分析】①按照一定的顺序数出线段的条数即可;②图中互补的角就是分别以C、D为顶点的两对邻补角,由此即可确定选择项;③根据角的和与差计算即可;④分两种情况探讨:当F在线段上最小,点F和E重合最大计算得出答案即可.
【详解】解:①以B、C、D、E为端点的线段共6条,故①正确;
②图中互补的角就是分别以C、D为顶点的两对邻补角,即和互补,和互补,故②错误;
③由,根据图形可以求出
,故③正确;
④当F在线段上,则点F到点B,C,D,E的距离之和最小为,当F和E重合,则点F到点B、C、D、E的距离之和最大为,④正确.
故选:C.
【点睛】此题分别考查了线段、角的和与差以及补角的定义,解题时注意:互为邻补角的两个角的和为180°.
6.A
【分析】根据余角和补角的定义得出结果.
【详解】解:∵一个角的度数为54°11′23″,
∴这个角的余角的度数为:90°-54°11′23″=35°48′37″;
补角的度数为:180°-54°11′23″=125°48′37″.
故选:A.
【点睛】本题考查了余角与补角的定义,主要记住互为余角的两个角的和为90度,互为补角的两个角的和为180度,比较简单.
7.A
【分析】根据点到直线的距离,垂线段最短即可求解.
【详解】解:∵,,,
∴到的距离为4.5,
点P是边BC上的动点,则AP的长不可能是4.
故选A.
【点睛】本题考查了点到直线的距离,垂线段最短,理解到的距离为4.5是解题的关键.
8.C
【分析】本题主要考查余角和补角,由垂直的定义得出,即,根据余角的性质可得答案.
【详解】解:∵,,
∴,
∴,
∴.
故选:C.
9.B
【分析】根据垂直的定义,由,得.由,根据角的和差关系得到.
【详解】解:∵,
∴.
∵,
∴.
故选:B.
【点睛】本题考查了垂线,余角的知识.要注意领会由垂直得直角这一要点.
10.B
【分析】用三角板的两条直角边中的一条与直线L重合,再另一条边直角边能与a、b、c、d中的那条边重合即可得解.
【详解】解:用三角板的两条直角边中的一条与直线l重合,再另一条边直角边能与b重合,
故选:B.
【点睛】本题主要是考查了两条直线垂直的性质,两条直线垂直其所夹的角为直角.
11.A
【分析】点到直线的距离是指垂线段的长度,据此逐一分析即可得到答案.
【详解】解:点到直线的距离是指垂线段的长度,
只有跳远的成绩按此评定,
故选:A.
【点睛】本题考查了点到直线的距离,解题关键是掌握点到直线的距离即垂线段的长度.
12.D
【解析】略
13.
【分析】本题考查的是垂线段最短,熟知“垂线段最短”是解答此题的关键. 根据垂线段最短即可得出结论.
【详解】解:∵小明的真实成绩为点P到直线的距离,
∴小明的真实成绩为米,
故答案为:.
14.116°
【分析】由图示可得,∠1与∠BOC互余,结合已知可求∠BOC,又因为∠2与∠COB互补,即可求出∠2的度数.
【详解】解:∵,∠AOC=90°,
∴∠BOC=64°,
∵∠2+∠BOC=180°,
∴∠2=116°.
故答案为:116°.
【点睛】此题考查了余角和补角的知识,属于基础题,关键是掌握互余的两角之和为90°,互补的两角之和为180°.
15.垂线段最短
【分析】本题考查了垂线段最短,利用了垂线段的性质:直线外的点与直线上任意一点的连线中垂线段最短.根据垂线段的性质,可得答案.
【详解】解:要把池中的水引到处,可过点引于,然后沿开渠,可使所开渠道最短,试说明设计的依据:垂线段最短.
故答案为:垂线段最短.
16.3
【分析】根据补角的性质、对顶角的性质,可得答案.
【详解】解:如图
,
∵∠1和∠3是对顶角.
∴∠1=∠3.
∵∠1+∠2=180°,∠2+∠4=180°,∠2+∠5=180°,
∴∠1=∠4=∠5,
故答案为:3.
【点睛】本题考查了对顶角、邻补角,利用补角的性质、对顶角的性质是解题关键.
17.8
【分析】根据点到直线的垂线段最短,再由面积求出高,即为AP的最小值,由题知,过点A作BC的垂线,即为所求,此时,该垂线也是三角形的高.
【详解】解:过点A作BC的垂线AP,根据点到直线的所有线段中,垂线段最短,
∴垂线段即为AP的最小值,
∵BC=5cm,ΔABC的面积为20,
∴,
∴AP=8,
故答案为:8.
【点睛】本题考查三角形的面积公式,垂线段最短的性质,属于基础题.
18.(1)
(2)
【分析】利用垂直定义和对顶角的性质可得答案;
设,,利用邻补角互补可得方程,然后解出的值,进而可得的度数,再利用对顶角的性质可得答案.
【详解】(1)解:,
,
,
,
;
(2)设,,
,
解得:,
,
,
,
,
.
【点睛】此题主要考查了垂线,以及对顶角,关键是掌握对顶角相等,理清图中角之间的关系.
19.
【分析】本题考查了与余角、补角有关的计算,互余的两个角和为,互补的两个角和为,据此即可求解.
【详解】解∶∵与互为余角,
∴,
∵,
∴,
∴的补角的度数为.
20.(1)8; 6
(2)图见解析;点C到的距离是
【分析】本题考查了点到直线的距离,熟练掌握点到直线的距离的概念及等面积法是解题的关键,
(1)根据点到直线的距离的概念进行求解即可得到答案;
(2)过点作,则线段表示点C到的距离,再利用等面积法即可求得线段的长.
【详解】(1)解:∵三角形为直角三角形,,,
∵,
∴点B到的距离是的长度为8,
∵
∴点A到的距离是的长度为6.
故答案为:8;6.
(2)解:过点作,如图,线段即为所求.
,即,
,
∴点C到的距离是.
21.(1)作图见解析
(2)作图见解析
(3)作图见解析,
【分析】(1)作射线即可;
(2)过点N作直线,使得即可;
(3)过点N作直线的垂线段;进而可得点N到直线的距离.
【详解】(1)
如图,射线即为所求;
(2)如图,直线即为所求;
(3)如图,垂线段即为所求;
所以点N到直线的距离是线段的长度.
故答案为:.
【点睛】本题考查了作图﹣复杂作图,垂线,点到直线的距离,平行线的性质,解决本题的关键是掌握基本作图方法.
22.见解析
【分析】本题考查了垂线段的性质,熟练掌握垂线段最短是解题的关键.过点作,交于点,根据垂线段最短解答即可.
【详解】解:过点作,交于点,
如图所示,点即为所求.
23.(1)见详解
(2)
(3)
【分析】本题主要垂线及其做图,点到直线的距离概念,垂线段最短,注意作图的准确性.
(1)根据网格结构的特点,利用直线与网格的夹角的关系找出与垂直的格点;
(2)根据点到直线的距离概念回答;
(3)根据垂线段最短直接回答即可.
【详解】(1)解:如图所示:
(2)解:线段的长度是点C到直线的距离,
故答案为:;
(3)解:连接,在线段中,线段最短,
理由:垂线段最短.
故答案为:.
24.(1)的度数为;(2),,还会相等;(3)变大;(4)见解析.
【分析】(1)根据∠AOC=90°,∠DOC=28°,求出∠AOD的度数,然后即可求出∠AOB的度数;
(2)根据直角和等式的性质可得,∠AOD=∠BOC;
(3)根据∠AOD+∠DOC+∠DOC+∠BOC=180°,可得∠AOB+∠DOC=180°,进而得到∠DOC变小∠AOB变大,若∠DOC越来越大,则∠AOB越来越小.
(4)首先以OE为边,在∠EOF外画∠GOE=90°,再以OF为边在∠EOF外画∠HOF=90°,即可得到∠HOG=∠EOF.
【详解】解:(1)因为,∠AOC=∠DOB=90°,∠DOC=28°
所以,∠COB=90°﹣28°=62°,
所以,∠AOB=90°+62°=152°,
(2)相等的角有:∠AOC=∠DOB=90°,∠AOD=∠BOC;
因为∠AOD=∠AOC-∠DOC=∠DOB-∠DOC=∠COB
所以∠AOD=∠BOC;
如果∠DOC≠28°,他们还会相等;
(3)因为∠AOB=∠AOC+∠DOB-∠DOC=180°-∠DOC
所以当∠DOC越来越小,则∠AOB越来越大;
当∠DOC越来越大,则∠AOB越来越小
(4)如图,
画∠BOD=∠COE=90°,则∠BOC=∠DOH
即,∠DOH为所画的角.
【点睛】本题考查了余角和补角,以及角的计算,是基础题,准确识图是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
