人教版八年级数学下册 18.2.3 正方形 同步测试(含详解)
文档属性
| 名称 | 人教版八年级数学下册 18.2.3 正方形 同步测试(含详解) |
|
|
| 格式 | docx | ||
| 文件大小 | 936.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 00:00:00 | ||
图片预览



文档简介
18.2.3 正方形同步测试
一、单选题
1.下列命题正确的是( )
A.正方形的对角线相等且互相平分 B.对角互补的四边形是平行四边形
C.矩形的对角线互相垂直 D.一组邻边相等的四边形是菱形
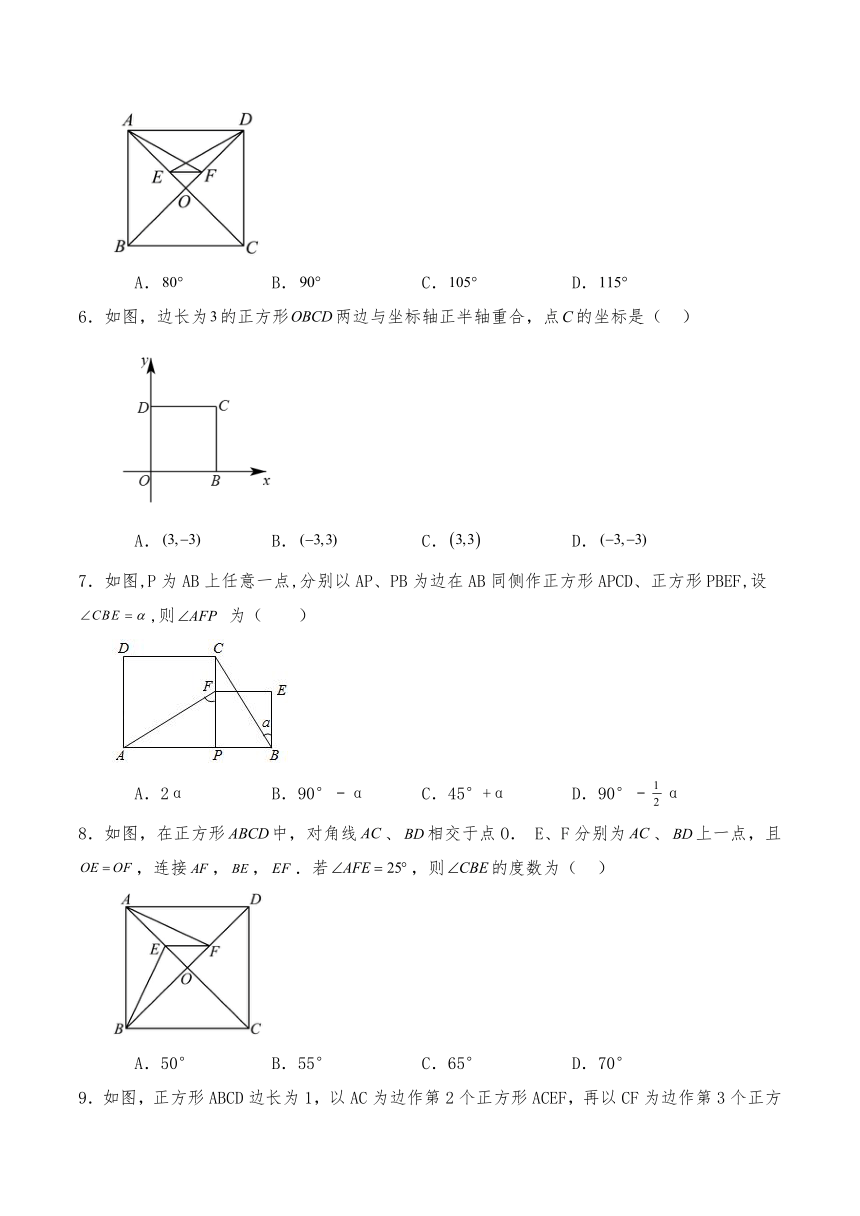
2.如图,在正方形中,点E,F分别是,的中点,,相交于点M,G为上一点,N为的中点.若,,则线段的长度为( )
A. B. C.2 D.
3.如图,在菱形中,,,顺次连接菱形各边中点、、、,则四边形的周长为( )
A. B. C. D.
4.若顺次连接四边形各边的中点所得的四边形是正方形,则四边形的两条对角线一定是( )
A.互相平分 B.互相垂直 C.互相平分且相等 D.互相垂直且相等
5.如图1,在正方形中,对角线相交于点O,E,F分别为,上的一点,且,连接.若,则的度数为( )
A. B. C. D.
6.如图,边长为的正方形两边与坐标轴正半轴重合,点的坐标是( )
A. B. C. D.
7.如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设,则 为( )
A.2α B.90°﹣α C.45°+α D.90°﹣α
8.如图,在正方形中,对角线、相交于点O. E、F分别为、上一点,且,连接,,.若,则的度数为( )
A.50° B.55° C.65° D.70°
9.如图,正方形ABCD边长为1,以AC为边作第2个正方形ACEF,再以CF为边作第3个正方形FCGH,…,按照这样的规律作下去,第6个正方形的边长为( )
A.(2)5 B.(2)6 C.()5 D.()6
10.如图,边长为的正方形的对角线与交于点,将正方形沿直线折叠,点落在对角线上的点处,折痕交于点,则( )
A. B. C. D.
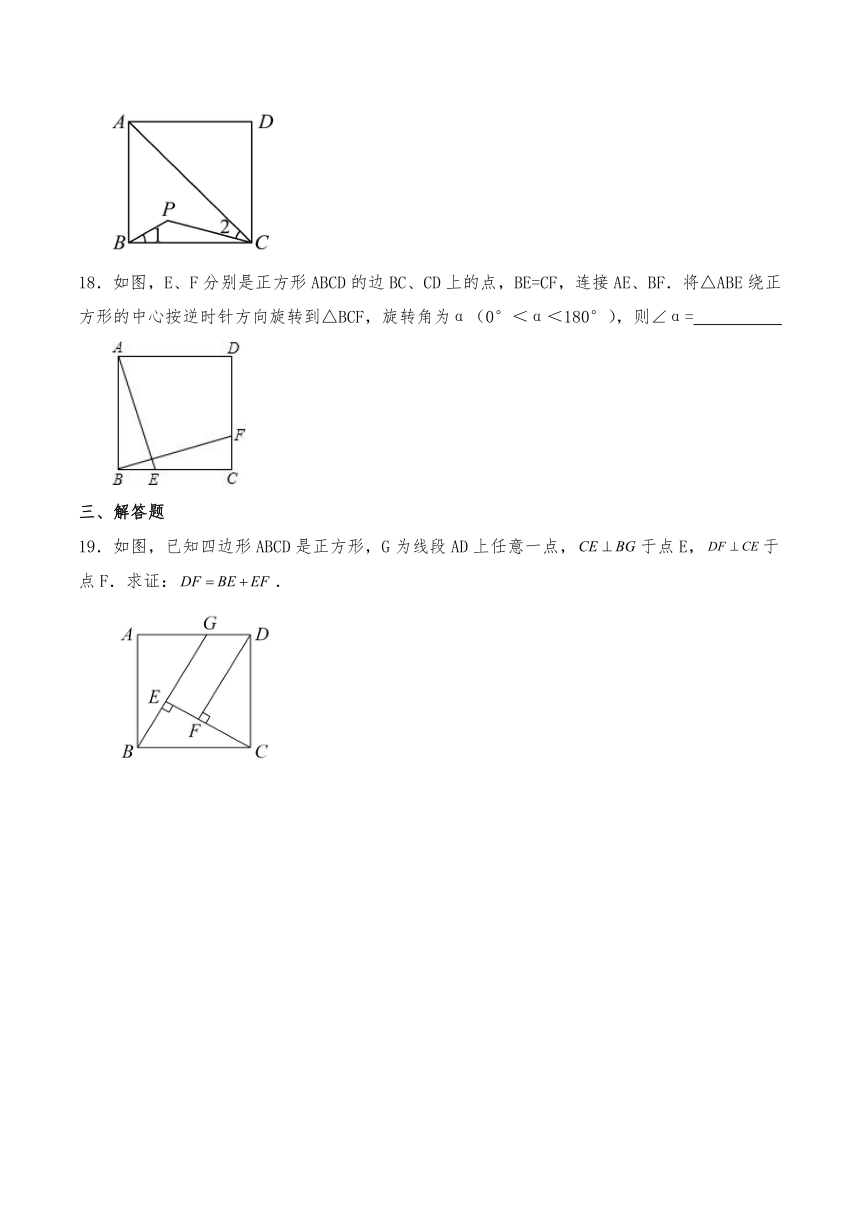
二、填空题
11.如图,矩形的对角线,相交于点O,再添加一个条件,使得四边形是正方形,这个条件可以是 (写出一个条件即可).
12.若直三棱柱的上下底面为正三角形,侧面展开图是边长为的正方形,则该直三棱柱的表面积为 .
13.如图,四边形是边长为4的正方形,是等边三角形,则阴影部分的面积为 .
14.七巧板是我国民间广为流传的一种益智玩具,某同学用边长为的正方形纸板制作了一副七巧板(如图),由5个等腰直角三角形,1个正方形和1个平行四边形组成.则图中阴影部分的面积为 .
15.如图,点是正方形的对角线上的一点,于点,.则点到直线的距离为 .
16.如图,正方形的边长为4,点E在边上,且,F为对角线上一动点,连接,,则的最小值为 .
17.如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为 °.
18.如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF.将△ABE绕正方形的中心按逆时针方向旋转到△BCF,旋转角为α(0°<α<180°),则∠α=
三、解答题
19.如图,已知四边形ABCD是正方形,G为线段AD上任意一点,于点E,于点F.求证:.
20.如图,在正方形ABCD中,点E,F在AC上,且AF=CE.求证:四边形BEDF是菱形.
21.如图,在正方形中,点是上的一点,点是延长线上的一点,且,连结.
(1)求证:≌;
(2)若,请求出的长.
22.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
23.如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M、N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
24.(1)如图1,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请你完成图形(尺规作图,不写做法,保留作图痕迹),并写出:BE与CD的数量关系 ;
(2)如图2,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE与CD,BE与CD有什么数量关系?说明理由;
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°、∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.
答案:
一、单选题
1.A
【分析】根据正方形、平行四边形、矩形、菱形的各自性质和构成条件进行判断即可.
解:A、正方形的对角线相等且互相垂直平分,描述正确;
B、对角互补的四边形不一定是平行四边形,只是内接于圆,描述错误;
C、矩形的对角线不一定垂直,但相等,描述错误;
D、一组邻边相等的平行四边形才构成菱形,描述错误.
故选:A.
2.B
【分析】根据条件正方形边长为4,由勾股定理求出线段长,利用中位线得到长即可.
解:连接,,
∵点E,F分别是,的中点,
∴四边形是矩形,
∴M是的中点,
在正方形中,,,
∴,
在中,由勾股定理得,
,
在中,M是的中点,N是的中点,
∴是的中位线,
∴.
故选:B.
3.C
【分析】首先利用三角形的中位线定理证得四边形为平行四边形,再求对角线长度,然后利用三角形中位线定理求出此平行四边形边长即可求出周长.
解:如图,连接、,相交于点,
点分别是边的中点,
,,
,同理,
四边形是平行四边形,
四边形是菱形, ,,
对角线互相垂直,
,
,
,,
是等边三角形,
,
在中,,,
,
,
,,
四边形的周长为.
故选:C.
4.D
【分析】由题意作出图形,然后根据正方形的判定定理可进行排除选项.
解:如图所示,点E、F、G、H分别是四边形ABCD边AD、DC、BC、AB的中点,
∴,
∴四边形EFGH是平行四边形,
对于A选项:对角线互相平分,四边形EFGH仍是平行四边形,故不符合题意;
对于B选项:对角线互相垂直,则有,可推出四边形EFGH是矩形,故不符合题意;
对于C选项:对角线互相平分且相等,则有,可推出四边形EFGH是菱形,故不符合题意;
对于D选项:对角线互相垂直且相等,则有,,可推出四边形EFGH是正方形,故符合题意;
故选D.
5.C
【分析】首先根据正方形的性质得到,,然后结合得到,然后证明出,最后利用三角形内角和定理求解即可.
解:∵四边形是正方形
∴,
∵
∴,
∴
∴
又∵,
∴
∴
∴
∴
故选:C.
6.C
【分析】根据正方形的性质,结合坐标的意义即可求解.
解:∵边长为的正方形两边与坐标轴正半轴重合,
∴
∴,
故选:C.
7.B
8.C
【分析】根据正方形的性质证明△AOF≌△BOE(SAS),得到∠OBE=∠OAF,利用OE=OF,∠EOF=90°,求出∠OEF=∠OFE=45°,由此得到∠OAF=∠OEF-∠AFE=20°,进而得到∠CBE的度数.
解:在正方形中,AO=BO,∠AOD=∠AOB=90°,∠CBO=45°,
∵,
∴△AOF≌△BOE(SAS),
∴∠OBE=∠OAF,
∵OE=OF,∠EOF=90°,
∴∠OEF=∠OFE=45°,
∵,
∴∠OAF=∠OEF-∠AFE=20°,
∴∠CBE=∠CBO+∠OBE=45°+20°=65°,
故选:C.
9.C
【分析】根据勾股定理得出正方形的对角线是边长的,第1个正方形的边长为1,其对角线长为;第2个正方形的边长为,其对角线长为;第3个正方形的边长为,其对角线长为; ;第n个正方形的边长为.所以,第6个正方形的边长.
解:由题知,第1个正方形的边长,
根据勾股定理得,第2个正方形的边长,
根据勾股定理得,第3个正方形的边长,
根据勾股定理得,第4个正方形的边长,
根据勾股定理得,第5个正方形的边长,
根据勾股定理得,第6个正方形的边长.
故选:C.
10.D
【分析】根据正方形的性质得到AB=AD=BC=CD=,∠DCB=∠COD=∠BOC=90°,OD=OC,求得BD=AB=2,得到OD=BO=OC=1,根据折叠的性质得到DE=DC=,DF⊥CE,求得OE=-1,根据全等三角形的性质即可得到结论.
解:∵四边形ABCD是正方形,
∴AB=AD=BC=CD=,∠DCB=∠COD=∠BOC=90°,OD=OC,
∴BD=AB=2,
∴OD=BO=OC=1,
∵将正方形ABCD沿直线DF折叠,点C落在对角线BD上的点E处,
∴DE=DC=,DF⊥CE,
∴OE=-1,∠EDF+∠FED=∠ECO+∠OEC=90°,
∴∠ODM=∠ECO,
在△OEC与△OMD中,
,
△OEC≌△OMD(ASA),
∴OM=OE=-1,
故选:D.
二、填空题
11.(答案不唯一)
【分析】根据正方形的判定定理即可得到结论.
解:这个条件可以是(答案不唯一),
理由:四边形是矩形,,
四边形是正方形,
故答案为:(答案不唯一).
12.
【分析】根据题意得出正三角形的边长为,进而根据表面积等于两个底面积加上侧面正方形的面积即可求解.
解:∵侧面展开图是边长为的正方形,
∴底面周长为,
∵底面为正三角形,
∴正三角形的边长为
作,
是等边三角形,,
,
在直角中,
,
;
∴该直三棱柱的表面积为,
故答案为:.
13.
【分析】作于点,于点,首先求出正方形的面积,然后根据等边三角形和正方形的性质求出和,从而求出和的面积,最后作差求解即可.
解:如图所示,作于点,于点,
∵四边形是边长为4的正方形,
∴,,,
∵是等边三角形,
∴,,,
∴,
∴,
∵,,
∴,
∴在中,,
∴,
∵,
∴,
故答案为:.
14.
【分析】根据正方形的性质,以及七巧板的特点,求得的长,即可求解.
解:如图所示,
依题意,,
∴图中阴影部分的面积为
故答案为:.
15.
【分析】过点作于,证明四边形四边形是正方形,即可求解.
解:如图所示,过点作于,
∵点是正方形的对角线上的一点,于点
∴四边形是矩形,
∴是等腰直角三角形,
∴
∴四边形是正方形,
∴,
即点到直线的距离为
故答案为:.
16.
【分析】连接交于一点F,连接,根据正方形的对称性得到此时最小,利用勾股定理求出即可.
解:如图,连接交于一点F,连接,
∵四边形是正方形,
∴点A与点C关于对称,
∴,
∴,此时最小,
∵正方形的边长为4,
∴,
∵点E在上,且,
∴,即的最小值为
故答案为:.
17.135
【分析】由正方形的性质可得∠ACB=∠BAC=45°,可得∠2+∠BCP=45°=∠1+∠BCP,由三角形内角和定理可求解.
解:∵四边形ABCD是正方形
∴∠ACB=∠BAC=45°
∴∠2+∠BCP=45°
∵∠1=∠2
∴∠1+∠BCP=45°
∵∠BPC=180°﹣∠1﹣∠BCP
∴∠BPC=135°
故答案为:135.
18.90°
解::∵四边形ABCD是正方形.
∴将△ABE绕正方形的中心按逆时针方向旋转到△BCF,∠α=90°,
故答案是:90°.
三、解答题
19.
解:证明:四边形是正方形,
,
,
,
,
,
,
在和中,,
,
,
,
.
20.
解:证明:连接BD交AC于O,
∵四边形ABCD是正方形,
∴BO=DO,AO=CO,AC⊥BD,
∵AF=CE,
∴EO=FO,
∴四边形DEBF是平行四边形,
又∵AC⊥BD,
∴平行四边形DEBF是菱形.
21.
解:(1)证明:∵四边形是正方形,
∴,,
在和中,
,
∴≌();
(2)解:∵≌,
∴,,
∵,
∴,即,
∴.
22.
解:(1)在正方形ABCD中,BC=CD,∠B=∠CDF=90°,
∵,
∴△CBE△CDF(SAS).
∴CE=CF.
(2)GE=BE+GD成立.
理由:∵由(1)得:△CBE△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,
又∵∠GCE=45°,
∴∠GCF=∠GCE=45°,CE=CF.
∵∠GCE=∠GCF, GC=GC,
∴△ECG△FCG(SAS).
∴GE=GF.
∴GE=DF+GD=BE+GD.
23.
解:证明:(1)∵对角线BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB;
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四边形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°
∴PM=MD,
∴四边形MPND是正方形.
24.
解:(1)根据题意,画出图形,如图所示:
BE=CD,理由如下:
∵△ABD和△ACE都是等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB,
在△CAD和△EAB中,
∵,
∴△CAD≌△EAB(SAS),
∴BE=CD;
(2)BE=CD,理由如下:
∵四边形ABFD和ACGE均为正方形,
∴AD=AB,AC=AE,∠BAD=∠CAE=90°,
∴∠CAD=∠EAB,
在△CAD和△EAB中,
∵,
∴△CAD≌△EAB(SAS).
∴BE=CD;
(3)过A作等腰直角三角形ABD,∠BAD=90°,连接CD,则AD=AB=100米,∠ABD=45°,∴米,
∵∠CAE=90°,
∴∠BAD=∠CAE,
∴∠CAD=∠BAE,
∵AC=AE,
∴△ACD≌△AEB,
∴CD=BE,
∵∠ABC=45°,
∴∠DBC=90°,
在Rt△DBC中,BC=100米,BD=100米,
∴(米),
∴BE=CD=米.
一、单选题
1.下列命题正确的是( )
A.正方形的对角线相等且互相平分 B.对角互补的四边形是平行四边形
C.矩形的对角线互相垂直 D.一组邻边相等的四边形是菱形
2.如图,在正方形中,点E,F分别是,的中点,,相交于点M,G为上一点,N为的中点.若,,则线段的长度为( )
A. B. C.2 D.
3.如图,在菱形中,,,顺次连接菱形各边中点、、、,则四边形的周长为( )
A. B. C. D.
4.若顺次连接四边形各边的中点所得的四边形是正方形,则四边形的两条对角线一定是( )
A.互相平分 B.互相垂直 C.互相平分且相等 D.互相垂直且相等
5.如图1,在正方形中,对角线相交于点O,E,F分别为,上的一点,且,连接.若,则的度数为( )
A. B. C. D.
6.如图,边长为的正方形两边与坐标轴正半轴重合,点的坐标是( )
A. B. C. D.
7.如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设,则 为( )
A.2α B.90°﹣α C.45°+α D.90°﹣α
8.如图,在正方形中,对角线、相交于点O. E、F分别为、上一点,且,连接,,.若,则的度数为( )
A.50° B.55° C.65° D.70°
9.如图,正方形ABCD边长为1,以AC为边作第2个正方形ACEF,再以CF为边作第3个正方形FCGH,…,按照这样的规律作下去,第6个正方形的边长为( )
A.(2)5 B.(2)6 C.()5 D.()6
10.如图,边长为的正方形的对角线与交于点,将正方形沿直线折叠,点落在对角线上的点处,折痕交于点,则( )
A. B. C. D.
二、填空题
11.如图,矩形的对角线,相交于点O,再添加一个条件,使得四边形是正方形,这个条件可以是 (写出一个条件即可).
12.若直三棱柱的上下底面为正三角形,侧面展开图是边长为的正方形,则该直三棱柱的表面积为 .
13.如图,四边形是边长为4的正方形,是等边三角形,则阴影部分的面积为 .
14.七巧板是我国民间广为流传的一种益智玩具,某同学用边长为的正方形纸板制作了一副七巧板(如图),由5个等腰直角三角形,1个正方形和1个平行四边形组成.则图中阴影部分的面积为 .
15.如图,点是正方形的对角线上的一点,于点,.则点到直线的距离为 .
16.如图,正方形的边长为4,点E在边上,且,F为对角线上一动点,连接,,则的最小值为 .
17.如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为 °.
18.如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF.将△ABE绕正方形的中心按逆时针方向旋转到△BCF,旋转角为α(0°<α<180°),则∠α=
三、解答题
19.如图,已知四边形ABCD是正方形,G为线段AD上任意一点,于点E,于点F.求证:.
20.如图,在正方形ABCD中,点E,F在AC上,且AF=CE.求证:四边形BEDF是菱形.
21.如图,在正方形中,点是上的一点,点是延长线上的一点,且,连结.
(1)求证:≌;
(2)若,请求出的长.
22.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
23.如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M、N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
24.(1)如图1,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请你完成图形(尺规作图,不写做法,保留作图痕迹),并写出:BE与CD的数量关系 ;
(2)如图2,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE与CD,BE与CD有什么数量关系?说明理由;
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°、∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.
答案:
一、单选题
1.A
【分析】根据正方形、平行四边形、矩形、菱形的各自性质和构成条件进行判断即可.
解:A、正方形的对角线相等且互相垂直平分,描述正确;
B、对角互补的四边形不一定是平行四边形,只是内接于圆,描述错误;
C、矩形的对角线不一定垂直,但相等,描述错误;
D、一组邻边相等的平行四边形才构成菱形,描述错误.
故选:A.
2.B
【分析】根据条件正方形边长为4,由勾股定理求出线段长,利用中位线得到长即可.
解:连接,,
∵点E,F分别是,的中点,
∴四边形是矩形,
∴M是的中点,
在正方形中,,,
∴,
在中,由勾股定理得,
,
在中,M是的中点,N是的中点,
∴是的中位线,
∴.
故选:B.
3.C
【分析】首先利用三角形的中位线定理证得四边形为平行四边形,再求对角线长度,然后利用三角形中位线定理求出此平行四边形边长即可求出周长.
解:如图,连接、,相交于点,
点分别是边的中点,
,,
,同理,
四边形是平行四边形,
四边形是菱形, ,,
对角线互相垂直,
,
,
,,
是等边三角形,
,
在中,,,
,
,
,,
四边形的周长为.
故选:C.
4.D
【分析】由题意作出图形,然后根据正方形的判定定理可进行排除选项.
解:如图所示,点E、F、G、H分别是四边形ABCD边AD、DC、BC、AB的中点,
∴,
∴四边形EFGH是平行四边形,
对于A选项:对角线互相平分,四边形EFGH仍是平行四边形,故不符合题意;
对于B选项:对角线互相垂直,则有,可推出四边形EFGH是矩形,故不符合题意;
对于C选项:对角线互相平分且相等,则有,可推出四边形EFGH是菱形,故不符合题意;
对于D选项:对角线互相垂直且相等,则有,,可推出四边形EFGH是正方形,故符合题意;
故选D.
5.C
【分析】首先根据正方形的性质得到,,然后结合得到,然后证明出,最后利用三角形内角和定理求解即可.
解:∵四边形是正方形
∴,
∵
∴,
∴
∴
又∵,
∴
∴
∴
∴
故选:C.
6.C
【分析】根据正方形的性质,结合坐标的意义即可求解.
解:∵边长为的正方形两边与坐标轴正半轴重合,
∴
∴,
故选:C.
7.B
8.C
【分析】根据正方形的性质证明△AOF≌△BOE(SAS),得到∠OBE=∠OAF,利用OE=OF,∠EOF=90°,求出∠OEF=∠OFE=45°,由此得到∠OAF=∠OEF-∠AFE=20°,进而得到∠CBE的度数.
解:在正方形中,AO=BO,∠AOD=∠AOB=90°,∠CBO=45°,
∵,
∴△AOF≌△BOE(SAS),
∴∠OBE=∠OAF,
∵OE=OF,∠EOF=90°,
∴∠OEF=∠OFE=45°,
∵,
∴∠OAF=∠OEF-∠AFE=20°,
∴∠CBE=∠CBO+∠OBE=45°+20°=65°,
故选:C.
9.C
【分析】根据勾股定理得出正方形的对角线是边长的,第1个正方形的边长为1,其对角线长为;第2个正方形的边长为,其对角线长为;第3个正方形的边长为,其对角线长为; ;第n个正方形的边长为.所以,第6个正方形的边长.
解:由题知,第1个正方形的边长,
根据勾股定理得,第2个正方形的边长,
根据勾股定理得,第3个正方形的边长,
根据勾股定理得,第4个正方形的边长,
根据勾股定理得,第5个正方形的边长,
根据勾股定理得,第6个正方形的边长.
故选:C.
10.D
【分析】根据正方形的性质得到AB=AD=BC=CD=,∠DCB=∠COD=∠BOC=90°,OD=OC,求得BD=AB=2,得到OD=BO=OC=1,根据折叠的性质得到DE=DC=,DF⊥CE,求得OE=-1,根据全等三角形的性质即可得到结论.
解:∵四边形ABCD是正方形,
∴AB=AD=BC=CD=,∠DCB=∠COD=∠BOC=90°,OD=OC,
∴BD=AB=2,
∴OD=BO=OC=1,
∵将正方形ABCD沿直线DF折叠,点C落在对角线BD上的点E处,
∴DE=DC=,DF⊥CE,
∴OE=-1,∠EDF+∠FED=∠ECO+∠OEC=90°,
∴∠ODM=∠ECO,
在△OEC与△OMD中,
,
△OEC≌△OMD(ASA),
∴OM=OE=-1,
故选:D.
二、填空题
11.(答案不唯一)
【分析】根据正方形的判定定理即可得到结论.
解:这个条件可以是(答案不唯一),
理由:四边形是矩形,,
四边形是正方形,
故答案为:(答案不唯一).
12.
【分析】根据题意得出正三角形的边长为,进而根据表面积等于两个底面积加上侧面正方形的面积即可求解.
解:∵侧面展开图是边长为的正方形,
∴底面周长为,
∵底面为正三角形,
∴正三角形的边长为
作,
是等边三角形,,
,
在直角中,
,
;
∴该直三棱柱的表面积为,
故答案为:.
13.
【分析】作于点,于点,首先求出正方形的面积,然后根据等边三角形和正方形的性质求出和,从而求出和的面积,最后作差求解即可.
解:如图所示,作于点,于点,
∵四边形是边长为4的正方形,
∴,,,
∵是等边三角形,
∴,,,
∴,
∴,
∵,,
∴,
∴在中,,
∴,
∵,
∴,
故答案为:.
14.
【分析】根据正方形的性质,以及七巧板的特点,求得的长,即可求解.
解:如图所示,
依题意,,
∴图中阴影部分的面积为
故答案为:.
15.
【分析】过点作于,证明四边形四边形是正方形,即可求解.
解:如图所示,过点作于,
∵点是正方形的对角线上的一点,于点
∴四边形是矩形,
∴是等腰直角三角形,
∴
∴四边形是正方形,
∴,
即点到直线的距离为
故答案为:.
16.
【分析】连接交于一点F,连接,根据正方形的对称性得到此时最小,利用勾股定理求出即可.
解:如图,连接交于一点F,连接,
∵四边形是正方形,
∴点A与点C关于对称,
∴,
∴,此时最小,
∵正方形的边长为4,
∴,
∵点E在上,且,
∴,即的最小值为
故答案为:.
17.135
【分析】由正方形的性质可得∠ACB=∠BAC=45°,可得∠2+∠BCP=45°=∠1+∠BCP,由三角形内角和定理可求解.
解:∵四边形ABCD是正方形
∴∠ACB=∠BAC=45°
∴∠2+∠BCP=45°
∵∠1=∠2
∴∠1+∠BCP=45°
∵∠BPC=180°﹣∠1﹣∠BCP
∴∠BPC=135°
故答案为:135.
18.90°
解::∵四边形ABCD是正方形.
∴将△ABE绕正方形的中心按逆时针方向旋转到△BCF,∠α=90°,
故答案是:90°.
三、解答题
19.
解:证明:四边形是正方形,
,
,
,
,
,
,
在和中,,
,
,
,
.
20.
解:证明:连接BD交AC于O,
∵四边形ABCD是正方形,
∴BO=DO,AO=CO,AC⊥BD,
∵AF=CE,
∴EO=FO,
∴四边形DEBF是平行四边形,
又∵AC⊥BD,
∴平行四边形DEBF是菱形.
21.
解:(1)证明:∵四边形是正方形,
∴,,
在和中,
,
∴≌();
(2)解:∵≌,
∴,,
∵,
∴,即,
∴.
22.
解:(1)在正方形ABCD中,BC=CD,∠B=∠CDF=90°,
∵,
∴△CBE△CDF(SAS).
∴CE=CF.
(2)GE=BE+GD成立.
理由:∵由(1)得:△CBE△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,
又∵∠GCE=45°,
∴∠GCF=∠GCE=45°,CE=CF.
∵∠GCE=∠GCF, GC=GC,
∴△ECG△FCG(SAS).
∴GE=GF.
∴GE=DF+GD=BE+GD.
23.
解:证明:(1)∵对角线BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB;
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四边形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°
∴PM=MD,
∴四边形MPND是正方形.
24.
解:(1)根据题意,画出图形,如图所示:
BE=CD,理由如下:
∵△ABD和△ACE都是等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB,
在△CAD和△EAB中,
∵,
∴△CAD≌△EAB(SAS),
∴BE=CD;
(2)BE=CD,理由如下:
∵四边形ABFD和ACGE均为正方形,
∴AD=AB,AC=AE,∠BAD=∠CAE=90°,
∴∠CAD=∠EAB,
在△CAD和△EAB中,
∵,
∴△CAD≌△EAB(SAS).
∴BE=CD;
(3)过A作等腰直角三角形ABD,∠BAD=90°,连接CD,则AD=AB=100米,∠ABD=45°,∴米,
∵∠CAE=90°,
∴∠BAD=∠CAE,
∴∠CAD=∠BAE,
∵AC=AE,
∴△ACD≌△AEB,
∴CD=BE,
∵∠ABC=45°,
∴∠DBC=90°,
在Rt△DBC中,BC=100米,BD=100米,
∴(米),
∴BE=CD=米.
