人教版八年级数学下册 第18章 平行四边形 章节复习卷 (含详解)
文档属性
| 名称 | 人教版八年级数学下册 第18章 平行四边形 章节复习卷 (含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 11:13:20 | ||
图片预览


文档简介
第18章《平行四边形》章节复习卷
一、单选题(本大题共10小题,每小题3分,共30分)
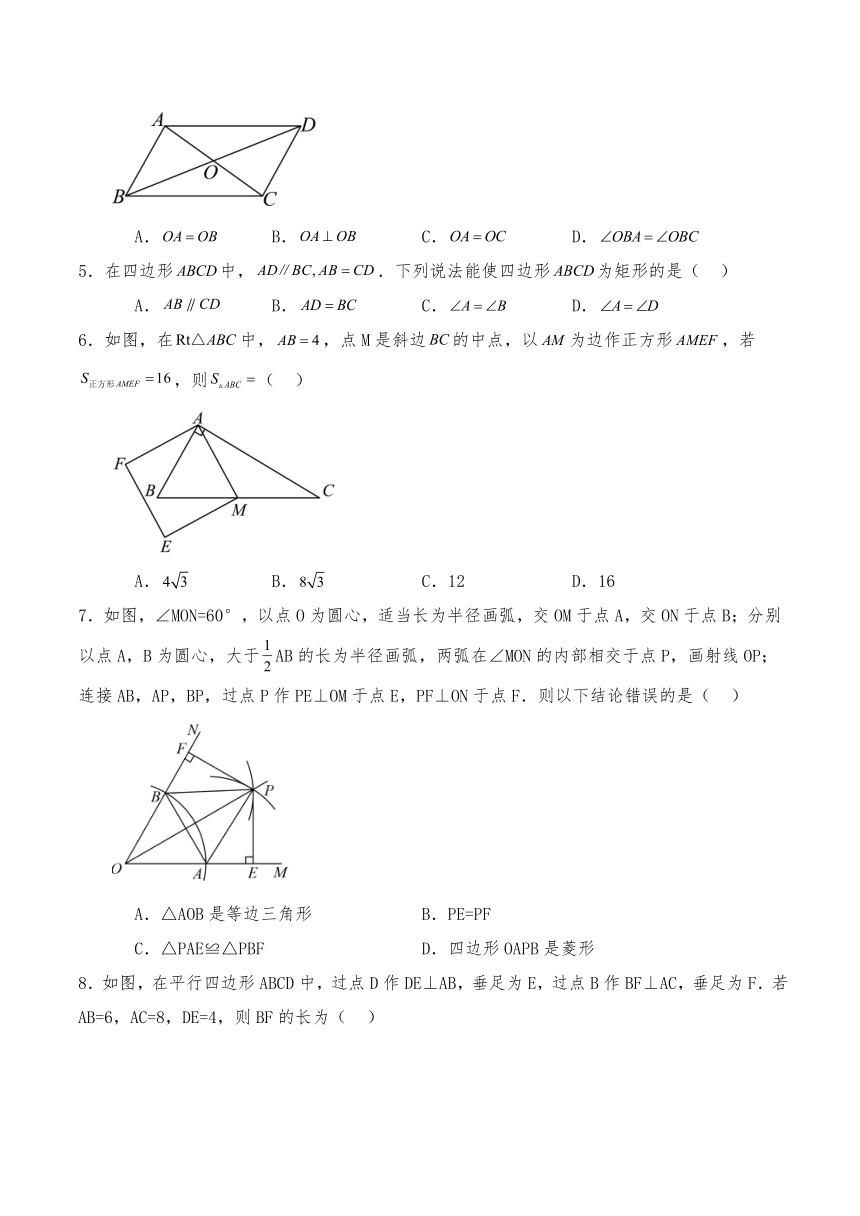
1.一技术人员用刻度尺(单位:)测量某三角形部件的尺寸.如图所示,已知,点D为边的中点,点A、B对应的刻度为1、7,则( )
A. B. C. D.
2.如图,矩形的对角线相交于点,下列结论一定正确的是( )
A.平分 B. C. D.
3.如图,两张宽为3的长方形纸条叠放在一起,已知,则阴影部分的面积是( )
A. B. C. D.
4.如图,平行四边形ABCD的对角线交于点,下列结论一定成立的是( )
A. B. C. D.
5.在四边形中,.下列说法能使四边形为矩形的是( )
A. B. C. D.
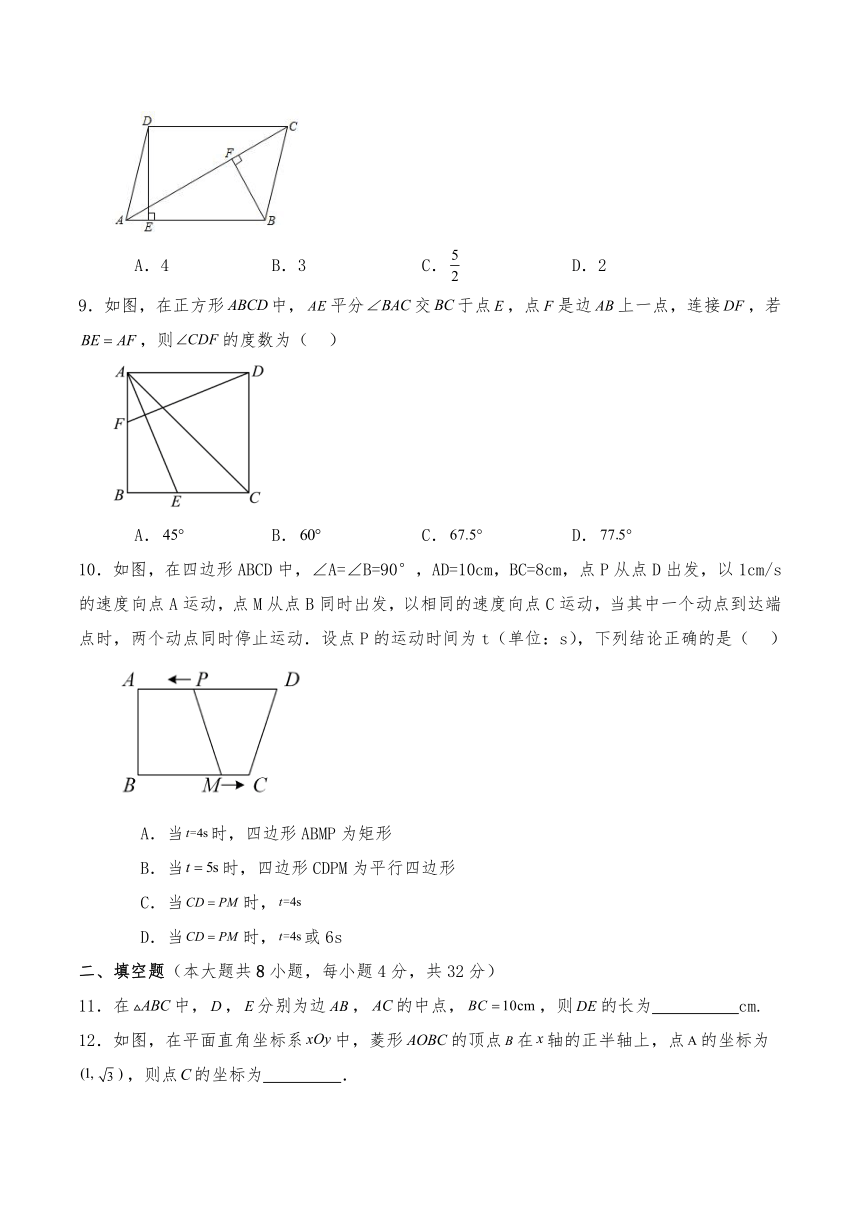
6.如图,在中,,点M是斜边的中点,以为边作正方形,若,则( )
A. B. C.12 D.16
7.如图,∠MON=60°,以点O为圆心,适当长为半径画弧,交OM于点A,交ON于点B;分别以点A,B为圆心,大于AB的长为半径画弧,两弧在∠MON的内部相交于点P,画射线OP;连接AB,AP,BP,过点P作PE⊥OM于点E,PF⊥ON于点F.则以下结论错误的是( )
A.△AOB是等边三角形 B.PE=PF
C.△PAE≌△PBF D.四边形OAPB是菱形
8.如图,在平行四边形ABCD中,过点D作DE⊥AB,垂足为E,过点B作BF⊥AC,垂足为F.若AB=6,AC=8,DE=4,则BF的长为( )
A.4 B.3 C. D.2
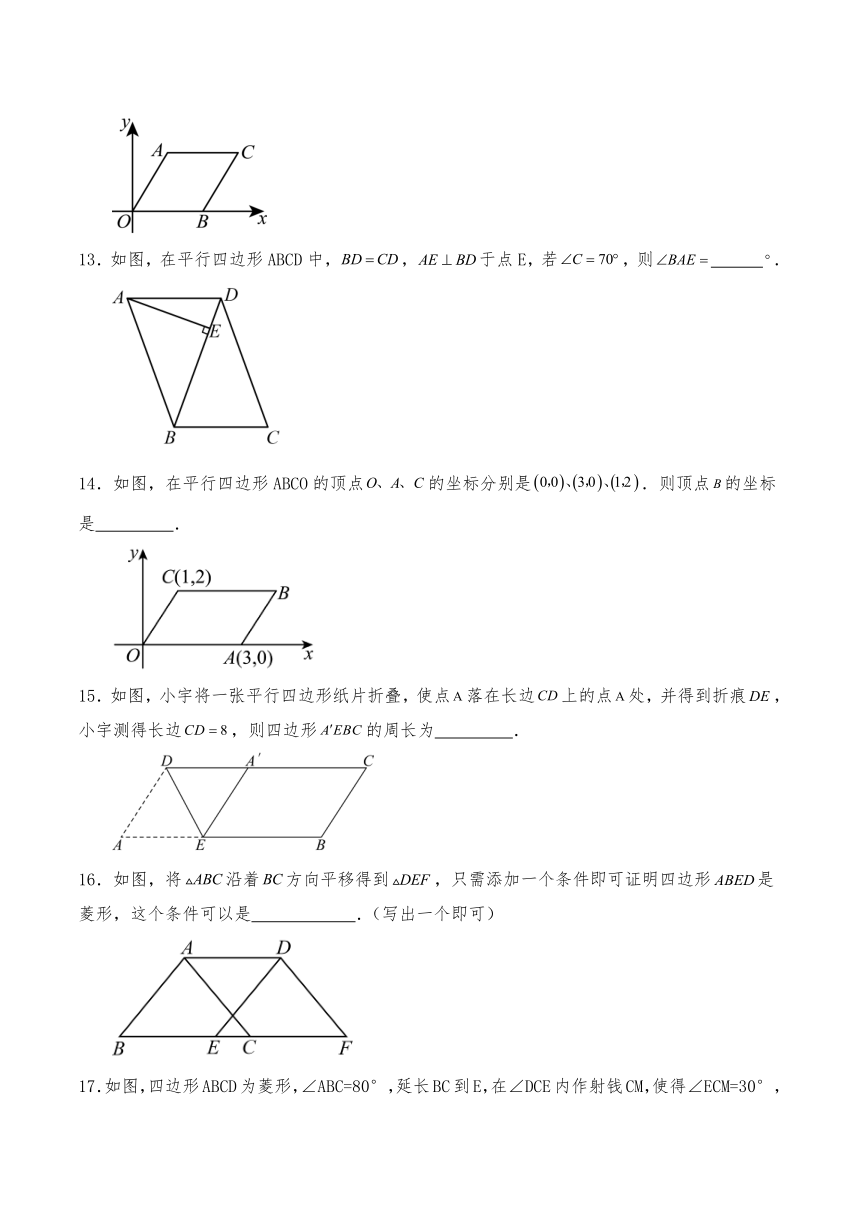
9.如图,在正方形中,平分交于点,点是边上一点,连接,若,则的度数为( )
A. B. C. D.
10.如图,在四边形ABCD中,∠A=∠B=90°,AD=10cm,BC=8cm,点P从点D出发,以1cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是( )
A.当时,四边形ABMP为矩形
B.当时,四边形CDPM为平行四边形
C.当时,
D.当时,或6s
二、填空题(本大题共8小题,每小题4分,共32分)
11.在中,,分别为边,的中点,,则的长为 cm.
12.如图,在平面直角坐标系中,菱形的顶点在轴的正半轴上,点的坐标为,则点的坐标为 .
13.如图,在平行四边形ABCD中,,于点E,若,则 .
14.如图,在平行四边形ABCO的顶点的坐标分别是.则顶点的坐标是 .
15.如图,小宇将一张平行四边形纸片折叠,使点落在长边上的点处,并得到折痕,小宇测得长边,则四边形的周长为 .
16.如图,将沿着方向平移得到,只需添加一个条件即可证明四边形是菱形,这个条件可以是 .(写出一个即可)
17.如图,四边形ABCD为菱形,∠ABC=80°,延长BC到E,在∠DCE内作射钱CM,使得∠ECM=30°,过点D作DF⊥CM,垂足为F.若DF=,则BD的长为 (结果保留很号).
18.菱形的边长为2,,点、分别是、上的动点,的最小值为 .
三、解答题(本大题共6小题,共58分)
19.(8分)如图,分别是的边上的点,已知,求证:.
20.(8分)如图,在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF.求证:
(1)△ABE≌△CDF;
(2)四边形AECF是平行四边形.
21.(10分)如图,在 ABCD中,点O为对角线BD的中点,EF过点O且分别交AB、DC于点E、F,连接DE、BF.
求证:
(1)△DOF≌△BOE;
(2)DE=BF.
22.(10分)在中,点D,F分别为边AC,AB的中点.延长DF到点E,使,连接BE.
(1)求证:;
(2)求证:四边形BCDE是平行四边形.
23.(10分)如图,将矩形纸片折叠,使点B与点D重合,点A落在点P处,折痕为.
(1)求证:;
(2)若,求的长.
24.(12分)如图所示,点在四边形的边上,连接,并延长交的延长线于点,已知,.
(1)求证:;
(2)若,求证:四边形为平行四边形.
答案:
一、单选题
1.B
【分析】由图求得的长度,结合直角三角形斜边上的中线等于斜边的一半即可求解.
解:由图可知,
在中,,点D为边的中点,
,
故选:B.
2.C
【分析】根据矩形的对角线相等,以及矩形与菱形性质的区别判断即可.
解:由矩形的对角线相交于点,
根据矩形的对角线相等,
可得.
故选:C.
3.D
【分析】首先过点作于点E,于点,由题意可得四边形是平行四边形,继而求得的长,判定四边形是菱形,则可求得答案.
解:过点作于点E,于点,
根据题意得:,,,
∴四边形是平行四边形,
∵,
∴,
∴,,
∵,,
∴,
同理: ,
∴,
∴四边形是菱形,
∴,
∴.
故选:D.
4.C
【分析】根据平行四边形性质逐项验证即可得到答案.
解:A、根据平行四边形性质:对角线相互平分,在在平行四边形ABCD中,,,则不一定成立,该选项不符合题意;
B、根据平行四边形性质:对角线相互平分,不一定垂直,则不一定成立,该选项不符合题意;
C、根据平行四边形性质:对角线相互平分,在在平行四边形ABCD中,,该选项符合题意;
D、根据平行四边形性质,对角线不一定平分对角,则不一定成立,该选项不符合题意;
故选:C.
5.C
【分析】结合平行四边形的判定和性质及矩形的判定逐一分析即可.
解:A:,
为平行四边形而非矩形
故A不符合题意
B:,
为平行四边形而非矩形
故B不符合题意
C:
∴∥
四边形为矩形
故C符合题意
D:
不是平行四边形也不是矩形
故D不符合题意
故选:C .
6.B
【分析】根据正方形的面积可求得的长,利用直角三角形斜边的中线求得斜边的长,利用勾股定理求得的长,根据三角形的面积公式即可求解.
解:∵,
∴,
∵中,点M是斜边的中点,
∴,
∴,
∴,
故选:B.
7.D
【分析】利用等边三角形的判定定理可判定选项A;根据角平分线的性质可判定选项B;利用HL可证明△PAE≌△PBF;利用菱形的判定定理可判定选项D.
解:∵∠MON=60°,OA=OB,∴△AOB是等边三角形,故选项A成立,不符合题意;
由作图知:射线OP是∠MON的平分线,且PE⊥OM,PF⊥ON,∴PE=PF,故选项B成立,不符合题意;
由作图知:AP=BP,又PE=PF,∴△PAE≌△PBF(HL) ,故选项C成立,不符合题意;
∵OA与AP不一定相等,∴四边形OAPB不一定是菱形,故选项D不成立,符合题意;
故选:D.
8.B
【分析】利用平行四边形ABCD的面积公式即可求解.
解:∵DE⊥AB,BF⊥AC,
∴S平行四边形ABCD=DE×AB=2××AC×BF,
∴4×6=2××8×BF,
∴BF=3,
故选:B.
9.C
【分析】先利用正方形的性质得到,,,利用角平分线的定义求得,再证得,利用全等三角形的性质求得,最后利用即可求解.
解:∵四边形是正方形,
∴,,,
∵平分交于点,
∴,
在和中,
,
∴,
∴ ,
∴,
故选:C
10.D
【分析】计算AP和BM的长,得到AP≠BM,判断选项A;计算PD和CM的长,得到PD≠CM,判断选项B;按PM=CD,且PM与CD不平行,或PM=CD,且PM∥CD分类讨论判断选项C和D.
解:由题意得PD=t,AP=AD-PD=10-t,BM=t,CM=8-t,∠A=∠B=90°,
A、当时,AP=10-t=6 cm,BM=4 cm,AP≠BM,则四边形ABMP不是矩形,该选项不符合题意;
B、当时,PD=5 cm,CM=8-5=3 cm,PD≠CM,则四边形CDPM不是平行四边形,该选项不符合题意;
作CE⊥AD于点E,则∠CEA=∠A=∠B=90°,
∴四边形ABCE是矩形,
∴BC=AE=8 cm,
∴DE=2 cm,
当PM=CD,且PM与CD不平行时,作MF⊥AD于点F,CE⊥AD于点E,
∴四边形CEFM是矩形,
∴FM=CE;
∴Rt△PFM≌Rt△DEC(HL),
∴PF=DE=2,EF=CM=8-t,
∴AP=10-4-(8-t)=10-t,
解得t=6 s;
当PM=CD,且PM∥CD时,
∴四边形CDPM是平行四边形,
∴DP=CM,
∴t=8-t,
解得t=4 s;
综上,当PM=CD时,t=4s或6s;选项C不符合题意;选项D符合题意;
故选:D.
二、填空题
11.
【分析】由于、分别为、边上的中点,那么是的中位线,根据三角形中位线定理可求.
解:如图所示,
、分别为、边上的中点,
是的中位线,
;
又∵,
∴;
故答案为:.
12.
【分析】根据点的坐标是,可得的长,再根据菱形的四条边都相等即可得点的坐标.
解:点的坐标是,
,
四边形为菱形,
,,
则点的坐标为.
故答案为:.
13.
【分析】证明,,由,可得,结合,可得.
解:∵,,
∴,,
∵在平行四边形ABCD,
∴,
∴,
∵,
∴;
故答案为:
14.
【分析】根据“平行四边形的对边平行且相等的性质”得到点的纵坐标与点的纵坐标相等,且,即可得到结果.
解:在中,,,
,
,
点的纵坐标与点的纵坐标相等,
,
故答案为:.
15.
【分析】可证,从而可得,再证四边形是平行四边形,可得,即可求解.
解:四边形是平行四边形,
,
,
由折叠得:,
,,
,
,
,
,
,
四边形是平行四边形,
.
故答案:.
16.AB=BE(答案不唯一)
【分析】由题目提供的条件可以得到四边形是平行四边形,再添加一个条件使其成为菱形即可.
解:添加AB=BE,
∵将沿着方向平移得到,
∴AB=DE,AB∥DE,
∴四边形ABED是平行四边形,
又∵AB=BE,
∴四边形是菱形,
故答案为:AB=BE(答案不唯一)
17.
【分析】连接AC交BD于H,证明△DCH≌△DCF,得出DH的长度,再根据菱形的性质得出BD的长度.
解:如图,连接AC交BD于点H,
由菱形的性质得∠ADC=∠ABC=80°,∠DCE=80°,∠DHC=90°,
又∵∠ECM=30°,
∴∠DCF=50°,
∵DF⊥CM,
∴∠CFD=90°,
∴∠CDF=40°,
又∵四边形ABCD是菱形,
∴BD平分∠ADC,
∴∠HDC=40°,
在△CDH和△CDF中,,
∴△CDH≌△CDF(AAS),
∴DH=DF=,
∴DB=2DH=.
故答案为:.
18.
【分析】过点C作CE⊥AB于E,交BD于G,根据轴对称确定最短路线问题以及垂线段最短可知CE为FG+CG的最小值,当P与点F重合,Q与G重合时,PQ+QC最小,在直角三角形BEC中,勾股定理即可求解.
解:如图,过点C作CE⊥AB于E,交BD于G,根据轴对称确定最短路线问题以及垂线段最短可知CE为FG+CG的最小值,当P与点F重合,Q与G重合时,PQ+QC最小,
菱形的边长为2,,
中,
PQ+QC的最小值为
故答案为:
三、解答题
19.
解:证明:∵四边形是平行四边形,
∴,,
在和中,
,
∴,
∴.
20.
(1)证明:解:∵四边形是平行四边形,
∴,,
∴,
又,
∴(SAS);
(2)证明:∵,
∴
∴,
∴四边形AECF是平行四边形
21.
解:(1)证明:∵四边形ABCD是平行四边形,O是BD的中点,
∴AB∥DC,OB=OD,
∴∠OBE=∠ODF.
在△BOE和△DOF中,,
∴△BOE≌△DOF(ASA);
(2)证明:∵△BOE≌△DOF,
∴EO=FO,
∵OB=OD,
∴四边形BEDF是平行四边形.
∴DE=BF.
22.
解:(1)证明:∵点F为边AB的中点,
∴,
在与中,
,
∴;
(2)证明:∵点D为边AC的中点,
∴,
由(1)得,
∴,,
∴,,
∴四边形BCDE是平行四边形.
23.
解:(1)∵四边形ABCD是矩形,
∴AB=CD,∠A=∠B=∠ADC=∠C=90°,
由折叠知,AB=PD,∠A=∠P,∠B=∠PDF=90°,
∴PD=CD,∠P=∠C,∠PDF =∠ADC,
∴∠PDF -∠EDF=∠ADC -∠EDF,
∴∠PDE=∠CDF,
在△PDE和△CDF中,
,
∴(ASA);
(2)如图,过点E作EG⊥BC交于点G,
∵四边形ABCD是矩形,
∴AB=CD=EG=4cm,
又∵EF=5cm,∴cm,
设AE=xcm,
∴EP=xcm,
由知,EP=CF=xcm,
∴DE=GC=GF+FC=3+x,
在Rt△PED中,,
即,
解得,,
∴BC=BG+GC= (cm).
24.
解:(1)证明:∵与是对顶角,
∴,
在与中,
,
∴
(2)证明:由(1)知,
∴,
∴,
∵点在的延长线上,
∴,
又∵,
∴四边形为平行四边形.
一、单选题(本大题共10小题,每小题3分,共30分)
1.一技术人员用刻度尺(单位:)测量某三角形部件的尺寸.如图所示,已知,点D为边的中点,点A、B对应的刻度为1、7,则( )
A. B. C. D.
2.如图,矩形的对角线相交于点,下列结论一定正确的是( )
A.平分 B. C. D.
3.如图,两张宽为3的长方形纸条叠放在一起,已知,则阴影部分的面积是( )
A. B. C. D.
4.如图,平行四边形ABCD的对角线交于点,下列结论一定成立的是( )
A. B. C. D.
5.在四边形中,.下列说法能使四边形为矩形的是( )
A. B. C. D.
6.如图,在中,,点M是斜边的中点,以为边作正方形,若,则( )
A. B. C.12 D.16
7.如图,∠MON=60°,以点O为圆心,适当长为半径画弧,交OM于点A,交ON于点B;分别以点A,B为圆心,大于AB的长为半径画弧,两弧在∠MON的内部相交于点P,画射线OP;连接AB,AP,BP,过点P作PE⊥OM于点E,PF⊥ON于点F.则以下结论错误的是( )
A.△AOB是等边三角形 B.PE=PF
C.△PAE≌△PBF D.四边形OAPB是菱形
8.如图,在平行四边形ABCD中,过点D作DE⊥AB,垂足为E,过点B作BF⊥AC,垂足为F.若AB=6,AC=8,DE=4,则BF的长为( )
A.4 B.3 C. D.2
9.如图,在正方形中,平分交于点,点是边上一点,连接,若,则的度数为( )
A. B. C. D.
10.如图,在四边形ABCD中,∠A=∠B=90°,AD=10cm,BC=8cm,点P从点D出发,以1cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是( )
A.当时,四边形ABMP为矩形
B.当时,四边形CDPM为平行四边形
C.当时,
D.当时,或6s
二、填空题(本大题共8小题,每小题4分,共32分)
11.在中,,分别为边,的中点,,则的长为 cm.
12.如图,在平面直角坐标系中,菱形的顶点在轴的正半轴上,点的坐标为,则点的坐标为 .
13.如图,在平行四边形ABCD中,,于点E,若,则 .
14.如图,在平行四边形ABCO的顶点的坐标分别是.则顶点的坐标是 .
15.如图,小宇将一张平行四边形纸片折叠,使点落在长边上的点处,并得到折痕,小宇测得长边,则四边形的周长为 .
16.如图,将沿着方向平移得到,只需添加一个条件即可证明四边形是菱形,这个条件可以是 .(写出一个即可)
17.如图,四边形ABCD为菱形,∠ABC=80°,延长BC到E,在∠DCE内作射钱CM,使得∠ECM=30°,过点D作DF⊥CM,垂足为F.若DF=,则BD的长为 (结果保留很号).
18.菱形的边长为2,,点、分别是、上的动点,的最小值为 .
三、解答题(本大题共6小题,共58分)
19.(8分)如图,分别是的边上的点,已知,求证:.
20.(8分)如图,在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF.求证:
(1)△ABE≌△CDF;
(2)四边形AECF是平行四边形.
21.(10分)如图,在 ABCD中,点O为对角线BD的中点,EF过点O且分别交AB、DC于点E、F,连接DE、BF.
求证:
(1)△DOF≌△BOE;
(2)DE=BF.
22.(10分)在中,点D,F分别为边AC,AB的中点.延长DF到点E,使,连接BE.
(1)求证:;
(2)求证:四边形BCDE是平行四边形.
23.(10分)如图,将矩形纸片折叠,使点B与点D重合,点A落在点P处,折痕为.
(1)求证:;
(2)若,求的长.
24.(12分)如图所示,点在四边形的边上,连接,并延长交的延长线于点,已知,.
(1)求证:;
(2)若,求证:四边形为平行四边形.
答案:
一、单选题
1.B
【分析】由图求得的长度,结合直角三角形斜边上的中线等于斜边的一半即可求解.
解:由图可知,
在中,,点D为边的中点,
,
故选:B.
2.C
【分析】根据矩形的对角线相等,以及矩形与菱形性质的区别判断即可.
解:由矩形的对角线相交于点,
根据矩形的对角线相等,
可得.
故选:C.
3.D
【分析】首先过点作于点E,于点,由题意可得四边形是平行四边形,继而求得的长,判定四边形是菱形,则可求得答案.
解:过点作于点E,于点,
根据题意得:,,,
∴四边形是平行四边形,
∵,
∴,
∴,,
∵,,
∴,
同理: ,
∴,
∴四边形是菱形,
∴,
∴.
故选:D.
4.C
【分析】根据平行四边形性质逐项验证即可得到答案.
解:A、根据平行四边形性质:对角线相互平分,在在平行四边形ABCD中,,,则不一定成立,该选项不符合题意;
B、根据平行四边形性质:对角线相互平分,不一定垂直,则不一定成立,该选项不符合题意;
C、根据平行四边形性质:对角线相互平分,在在平行四边形ABCD中,,该选项符合题意;
D、根据平行四边形性质,对角线不一定平分对角,则不一定成立,该选项不符合题意;
故选:C.
5.C
【分析】结合平行四边形的判定和性质及矩形的判定逐一分析即可.
解:A:,
为平行四边形而非矩形
故A不符合题意
B:,
为平行四边形而非矩形
故B不符合题意
C:
∴∥
四边形为矩形
故C符合题意
D:
不是平行四边形也不是矩形
故D不符合题意
故选:C .
6.B
【分析】根据正方形的面积可求得的长,利用直角三角形斜边的中线求得斜边的长,利用勾股定理求得的长,根据三角形的面积公式即可求解.
解:∵,
∴,
∵中,点M是斜边的中点,
∴,
∴,
∴,
故选:B.
7.D
【分析】利用等边三角形的判定定理可判定选项A;根据角平分线的性质可判定选项B;利用HL可证明△PAE≌△PBF;利用菱形的判定定理可判定选项D.
解:∵∠MON=60°,OA=OB,∴△AOB是等边三角形,故选项A成立,不符合题意;
由作图知:射线OP是∠MON的平分线,且PE⊥OM,PF⊥ON,∴PE=PF,故选项B成立,不符合题意;
由作图知:AP=BP,又PE=PF,∴△PAE≌△PBF(HL) ,故选项C成立,不符合题意;
∵OA与AP不一定相等,∴四边形OAPB不一定是菱形,故选项D不成立,符合题意;
故选:D.
8.B
【分析】利用平行四边形ABCD的面积公式即可求解.
解:∵DE⊥AB,BF⊥AC,
∴S平行四边形ABCD=DE×AB=2××AC×BF,
∴4×6=2××8×BF,
∴BF=3,
故选:B.
9.C
【分析】先利用正方形的性质得到,,,利用角平分线的定义求得,再证得,利用全等三角形的性质求得,最后利用即可求解.
解:∵四边形是正方形,
∴,,,
∵平分交于点,
∴,
在和中,
,
∴,
∴ ,
∴,
故选:C
10.D
【分析】计算AP和BM的长,得到AP≠BM,判断选项A;计算PD和CM的长,得到PD≠CM,判断选项B;按PM=CD,且PM与CD不平行,或PM=CD,且PM∥CD分类讨论判断选项C和D.
解:由题意得PD=t,AP=AD-PD=10-t,BM=t,CM=8-t,∠A=∠B=90°,
A、当时,AP=10-t=6 cm,BM=4 cm,AP≠BM,则四边形ABMP不是矩形,该选项不符合题意;
B、当时,PD=5 cm,CM=8-5=3 cm,PD≠CM,则四边形CDPM不是平行四边形,该选项不符合题意;
作CE⊥AD于点E,则∠CEA=∠A=∠B=90°,
∴四边形ABCE是矩形,
∴BC=AE=8 cm,
∴DE=2 cm,
当PM=CD,且PM与CD不平行时,作MF⊥AD于点F,CE⊥AD于点E,
∴四边形CEFM是矩形,
∴FM=CE;
∴Rt△PFM≌Rt△DEC(HL),
∴PF=DE=2,EF=CM=8-t,
∴AP=10-4-(8-t)=10-t,
解得t=6 s;
当PM=CD,且PM∥CD时,
∴四边形CDPM是平行四边形,
∴DP=CM,
∴t=8-t,
解得t=4 s;
综上,当PM=CD时,t=4s或6s;选项C不符合题意;选项D符合题意;
故选:D.
二、填空题
11.
【分析】由于、分别为、边上的中点,那么是的中位线,根据三角形中位线定理可求.
解:如图所示,
、分别为、边上的中点,
是的中位线,
;
又∵,
∴;
故答案为:.
12.
【分析】根据点的坐标是,可得的长,再根据菱形的四条边都相等即可得点的坐标.
解:点的坐标是,
,
四边形为菱形,
,,
则点的坐标为.
故答案为:.
13.
【分析】证明,,由,可得,结合,可得.
解:∵,,
∴,,
∵在平行四边形ABCD,
∴,
∴,
∵,
∴;
故答案为:
14.
【分析】根据“平行四边形的对边平行且相等的性质”得到点的纵坐标与点的纵坐标相等,且,即可得到结果.
解:在中,,,
,
,
点的纵坐标与点的纵坐标相等,
,
故答案为:.
15.
【分析】可证,从而可得,再证四边形是平行四边形,可得,即可求解.
解:四边形是平行四边形,
,
,
由折叠得:,
,,
,
,
,
,
,
四边形是平行四边形,
.
故答案:.
16.AB=BE(答案不唯一)
【分析】由题目提供的条件可以得到四边形是平行四边形,再添加一个条件使其成为菱形即可.
解:添加AB=BE,
∵将沿着方向平移得到,
∴AB=DE,AB∥DE,
∴四边形ABED是平行四边形,
又∵AB=BE,
∴四边形是菱形,
故答案为:AB=BE(答案不唯一)
17.
【分析】连接AC交BD于H,证明△DCH≌△DCF,得出DH的长度,再根据菱形的性质得出BD的长度.
解:如图,连接AC交BD于点H,
由菱形的性质得∠ADC=∠ABC=80°,∠DCE=80°,∠DHC=90°,
又∵∠ECM=30°,
∴∠DCF=50°,
∵DF⊥CM,
∴∠CFD=90°,
∴∠CDF=40°,
又∵四边形ABCD是菱形,
∴BD平分∠ADC,
∴∠HDC=40°,
在△CDH和△CDF中,,
∴△CDH≌△CDF(AAS),
∴DH=DF=,
∴DB=2DH=.
故答案为:.
18.
【分析】过点C作CE⊥AB于E,交BD于G,根据轴对称确定最短路线问题以及垂线段最短可知CE为FG+CG的最小值,当P与点F重合,Q与G重合时,PQ+QC最小,在直角三角形BEC中,勾股定理即可求解.
解:如图,过点C作CE⊥AB于E,交BD于G,根据轴对称确定最短路线问题以及垂线段最短可知CE为FG+CG的最小值,当P与点F重合,Q与G重合时,PQ+QC最小,
菱形的边长为2,,
中,
PQ+QC的最小值为
故答案为:
三、解答题
19.
解:证明:∵四边形是平行四边形,
∴,,
在和中,
,
∴,
∴.
20.
(1)证明:解:∵四边形是平行四边形,
∴,,
∴,
又,
∴(SAS);
(2)证明:∵,
∴
∴,
∴四边形AECF是平行四边形
21.
解:(1)证明:∵四边形ABCD是平行四边形,O是BD的中点,
∴AB∥DC,OB=OD,
∴∠OBE=∠ODF.
在△BOE和△DOF中,,
∴△BOE≌△DOF(ASA);
(2)证明:∵△BOE≌△DOF,
∴EO=FO,
∵OB=OD,
∴四边形BEDF是平行四边形.
∴DE=BF.
22.
解:(1)证明:∵点F为边AB的中点,
∴,
在与中,
,
∴;
(2)证明:∵点D为边AC的中点,
∴,
由(1)得,
∴,,
∴,,
∴四边形BCDE是平行四边形.
23.
解:(1)∵四边形ABCD是矩形,
∴AB=CD,∠A=∠B=∠ADC=∠C=90°,
由折叠知,AB=PD,∠A=∠P,∠B=∠PDF=90°,
∴PD=CD,∠P=∠C,∠PDF =∠ADC,
∴∠PDF -∠EDF=∠ADC -∠EDF,
∴∠PDE=∠CDF,
在△PDE和△CDF中,
,
∴(ASA);
(2)如图,过点E作EG⊥BC交于点G,
∵四边形ABCD是矩形,
∴AB=CD=EG=4cm,
又∵EF=5cm,∴cm,
设AE=xcm,
∴EP=xcm,
由知,EP=CF=xcm,
∴DE=GC=GF+FC=3+x,
在Rt△PED中,,
即,
解得,,
∴BC=BG+GC= (cm).
24.
解:(1)证明:∵与是对顶角,
∴,
在与中,
,
∴
(2)证明:由(1)知,
∴,
∴,
∵点在的延长线上,
∴,
又∵,
∴四边形为平行四边形.
