浙江2025年中考解答题专题——解直角三角形(含解析)
文档属性
| 名称 | 浙江2025年中考解答题专题——解直角三角形(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 15:04:20 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙江中考解答题专题——解直角三角形(含解析)
1.(2025·金华模拟)如图1,是一台小型输送机,其示意图如图2所示.已知两个支架的端点的距离,传输带与支架所成的角,支架端点离地面的高度,求支架端点离地面的高度.(结果精确到0.1m;参考数据,,).
2.(2024九下·南陵模拟)《海岛算经》是中国古代测量术的代表作,原名《重差》.这本著作建立起了从直接测量向间接测量的桥梁.直至近代,重差测量法仍有借鉴意义.
如图,为测量海岛上一座山峰的高度,直立两根高2米的标杆和,两杆间距相距6米,D、B、H三点共线.从点B处退行到点F,观察山顶A,发现A、C、F三点共线,且仰角为;从点D处退行到点G,观察山顶A,发现A、E、G三点共线,且仰角为.(点F、G都在直线上)
(1)求的长(结果保留根号);
(2)山峰高度的长(结果精确到米).
(参考数据:,)
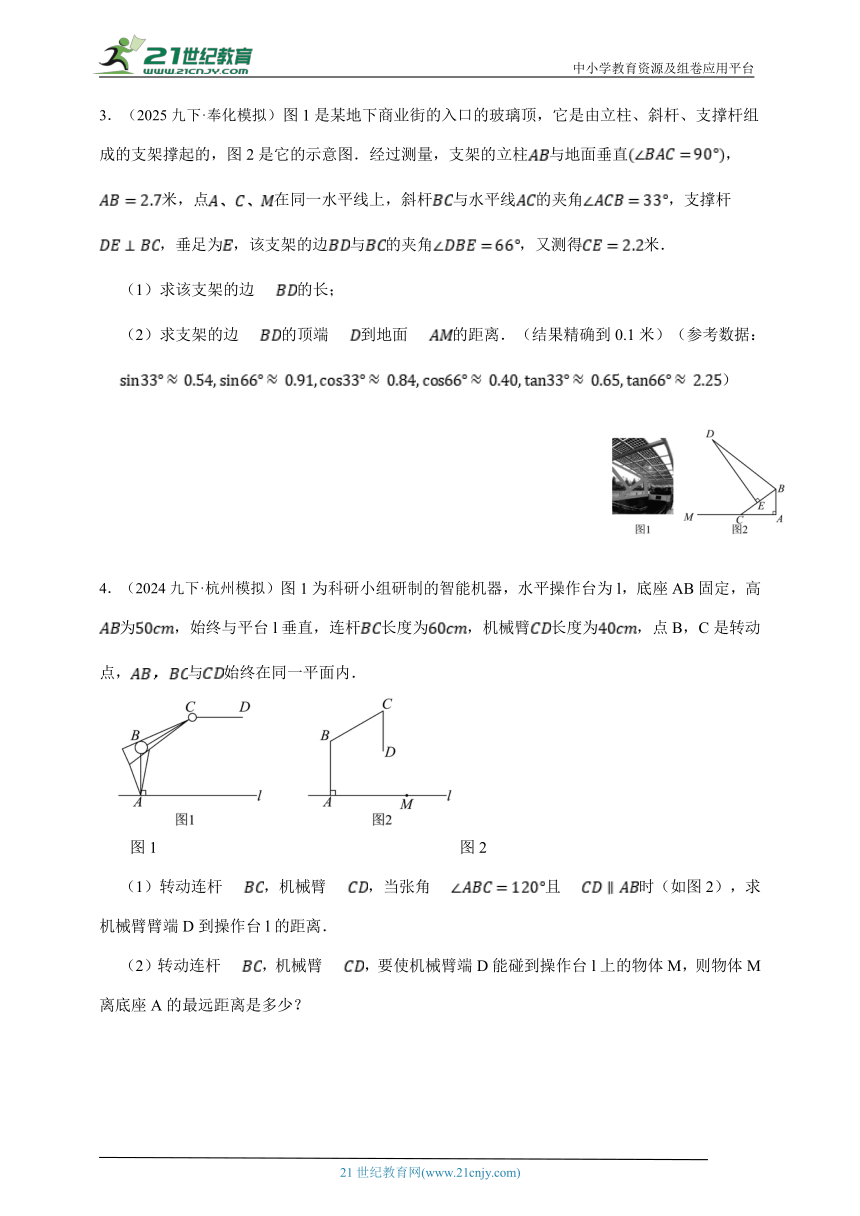
3.(2025九下·奉化模拟)图1是某地下商业街的入口的玻璃顶,它是由立柱、斜杆、支撑杆组成的支架撑起的,图2是它的示意图.经过测量,支架的立柱与地面垂直,米,点在同一水平线上,斜杆与水平线的夹角,支撑杆,垂足为,该支架的边与的夹角,又测得米.
(1)求该支架的边的长;
(2)求支架的边的顶端到地面的距离.(结果精确到0.1米)(参考数据:)
4.(2024九下·杭州模拟)图1为科研小组研制的智能机器,水平操作台为l,底座AB固定,高为,始终与平台l垂直,连杆长度为,机械臂长度为,点B,C是转动点,与始终在同一平面内.
图1 图2
(1)转动连杆,机械臂,当张角且时(如图2),求机械臂臂端D到操作台l的距离.
(2)转动连杆,机械臂,要使机械臂端D能碰到操作台l上的物体M,则物体M离底座A的最远距离是多少?
5.(2024九下·浙江模拟)如图是水槽水龙头(图1)的侧面平面示意图,矩形为水槽侧面,有,在水槽边上方安装水管,水龙头,其中.测得,.
(1)求点F离水槽底的高度.
(2)若水柱与共线,当手伸到水槽内洗手时(即手与水柱的交点在下面),水不会溅出.当手与水柱交点P离水槽壁的距离为,洗手时水会不会溅出?试通过计算说明.(参考数据:)
6.(2025·绍兴模拟)综合与实践活动中,某数学兴趣小组利用所学的知识测量矩形广告牌的高度.
如图,在地面处测得广告牌顶端顶点的仰角为,走向广告牌到达处,在处测得广告牌低端顶点的仰角为,已知,立柱垂直于,且点,,在同一条水平直线上.(矩形广告牌与立柱垂直)过点作,垂足为.设(单位:).
(1)用含有和的式子表示线段的长;
(2)求广告牌低端顶点到地面的距离的长.(取,结果取整数)
7.(2024九下·柯桥模拟)随着时代的发展,手机“直播带货”已经成为当前最为强劲的购物新潮流.某种手机支架如图1所示,立杆垂直于地面,其高为,为支杆,它可绕点旋转,其中长为,为悬杆,滑动悬杆可调节的长度.(参考数据:,,)
(1)如图2,当、、三点共线,时,且支杆与立杆之间的夹角为,求端点距离地面的高度;
(2)调节支杆,悬杆,使得,,如图3所示,且点到地面的距离为,求的长.(结果精确到)
8.(2025九下·定海模拟)有一种升降熨烫台如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度.图2是这种升降熨烫台的平面示意图.AB和CD是两根相同长度的活动支撑杆,点O是它们的连接点,OA=OC,h(cm)表示熨烫台的高度.
(1)如图2﹣1.若AB=CD=110cm,∠AOC=120°,求h的值;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度为120cm时,两根支撑杆的夹角∠AOC是74°(如图2﹣2).求该熨烫台支撑杆AB的长度(结果精确到1cm).
(参考数据:sin37°≈0.6,cos37°≈0.8,sin53°≈0.8,cos53°≈0.6.)
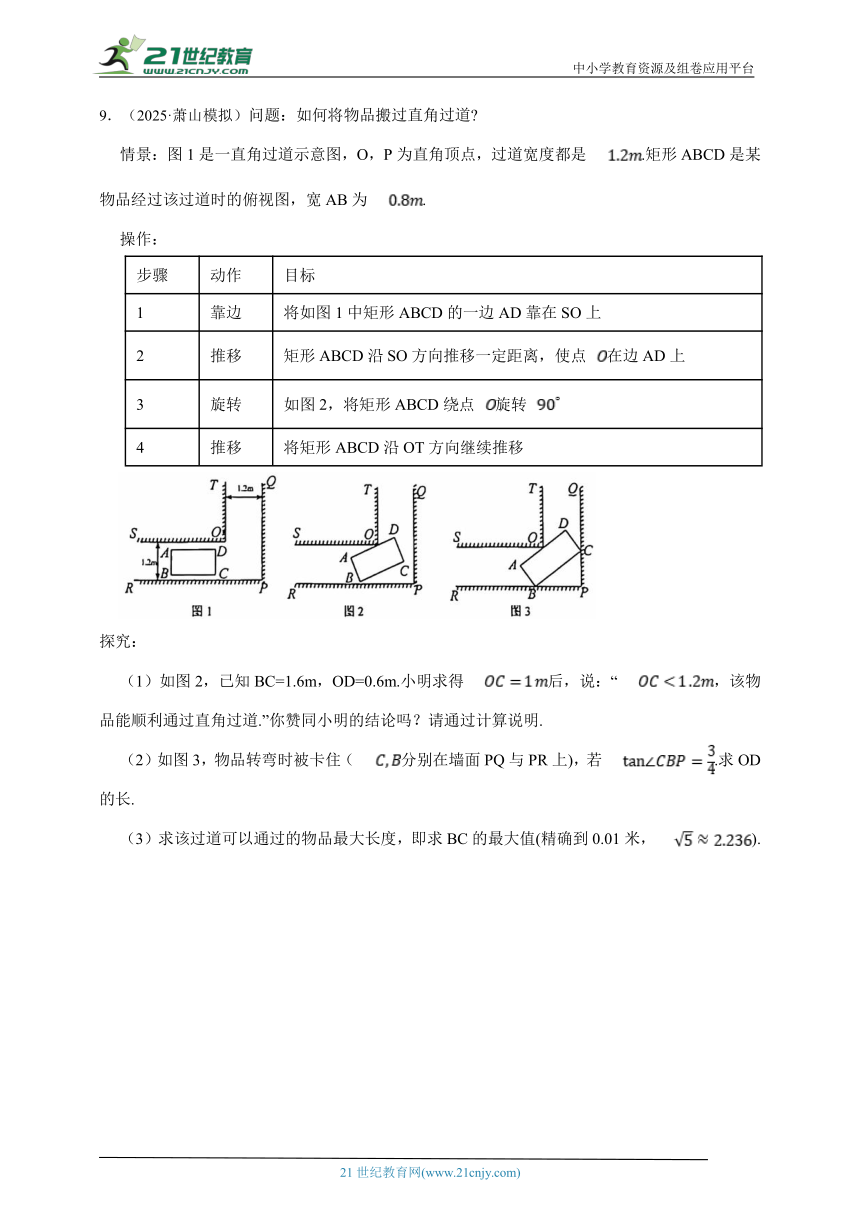
9.(2025·萧山模拟)问题:如何将物品搬过直角过道
情景:图1是一直角过道示意图,O,P为直角顶点,过道宽度都是.矩形ABCD是某物品经过该过道时的俯视图,宽AB为.
操作:
步骤 动作 目标
1 靠边 将如图1中矩形ABCD的一边AD靠在SO上
2 推移 矩形ABCD沿SO方向推移一定距离,使点在边AD上
3 旋转 如图2,将矩形ABCD绕点旋转
4 推移 将矩形ABCD沿OT方向继续推移
探究:
(1)如图2,已知BC=1.6m,OD=0.6m.小明求得后,说:“,该物品能顺利通过直角过道.”你赞同小明的结论吗?请通过计算说明.
(2)如图3,物品转弯时被卡住(分别在墙面PQ与PR上),若.求OD的长.
(3)求该过道可以通过的物品最大长度,即求BC的最大值(精确到0.01米,).
10.(2024九下·杭州模拟)如图,玻璃桌面与地面平行、桌面上有一盏台灯和一支铅笔,点光源O与铅笔所确定的平面垂直于桌面.在灯光照射下,在地面上形成的影子为(不计折射),.
(1)在桌面上沿着方向平移铅笔,试说明的长度不变.
(2)桌面上一点P恰在点O的正下方,且,,,桌面的高度为.在点O与所确定的平面内,将绕点A旋转,使得的长度最大.
①画出此时所在位置的示意图;
②的长度的最大值为 cm.
答案解析部分
1.【答案】解:过点作于点,可得,在中,,
∴
∴
【解析】【分析】过点A作于点 F,可得CF长,然后在中根据余弦的定义求BF长解题即可.
2.【答案】(1)解:由题意得:,,
在中,,,
(米),
在中,,,
(米),
米,
米,
的长为米;
(2)解:设米,在中,,
(米),
∵米,
米,
在中,,
,
,
解得:,
米,
∴山峰高度的长约为米.
【解析】【分析】(1)根据题意得到,,然后在和中,利用解直角三角形求出和的长,解题即可;
(2)设米,在中,利用锐角三角函数的定义得到的长,从而表示长,再在中,利用解直角三角形可得,列方程解题即可.
3.【答案】(1)解:由题意得,,,
∴.
∵
∴.
∵,
∴,
∵
∴.
答:该支架的边的长7米.
(2)解:过点作,垂足为,过点作,垂足为G.则,
∵,
∴四边形是矩形,
∵,
∴.
∵,
∴.
∴,
∵,
∴.
答:支架的边的顶端到地面的距离为6.5米.
【解析】【分析】(1)先根据正弦的定义求出BC长,然后在Rt△BDE中利用余弦解题即可.
(2)过点作,垂足为,过点作,垂足为G.即可得到四边形是矩形,进而求出.然后根据正弦求出DG长解题即可.
(1)解:由题意得,,,
∴.
∵
∴.
∵,
∴,
∵
∴.
答:该支架的边的长7米.
(2)解:过点作,垂足为,过点作,垂足为G.
则,
∵,
∴四边形是矩形,
∵,
∴.
∵,
∴.
∴,
∵,
∴.
答:支架的边的顶端到地面的距离为6.5米.
4.【答案】(1)解:过点B作,垂足为F,延长交l于点E,如图,
则,
∵,
∴,
在中,,
∴,
∴,
∴,
∴机械臂臂端D到操作台l的距离为;
(2)解:当B、C、D三点共线时,此时M点与底座距离最远,如图:
∵,
∴,
在中,,
∴,
∴物体M离底座A的最远距离为.
【解析】【分析】(1)过点B作,垂足为F,根据题意可得,,从而可得,然后在中,利用锐角三角函数的定义sin∠CBF=求出的长,从而求出的长,然后根据线段的构成DE=CE-CD即可求解;
(2)当B、C、D三点共线时,此时M点与底座距离最远,由线段的构成BD=BC+CD求出BD的值,在Rt△ABD中,用勾股定理计算即可求解.
(1)解:过点B作,垂足为F,延长交l于点E,如图,
则,
∵,
∴,
在中,,
∴,
∴,
∴,
∴机械臂臂端D到操作台l的距离为;
(2)解:当B、C、D三点共线时,此时M点与底座距离最远,如图:
∵,
∴,
在中,,
∴,
∴物体M离底座A的最远距离为
5.【答案】(1)解:如图,过点E作,∵,,
∴四边形是矩形,
∵,,
∴,,
∵,
∴,
∴;
(2)解:水不会溅出由(1)可得,,,
在中,,
∴,
作交于点L,,
∵,,
∴,
∵在中,,
∴,
∴水不会溅出.
【解析】【分析】(1)要求FM的高度,可过点E作FM的垂线段AN,由矩形性质知,;由题意知,//,则与互补,又已知,解 求出即可;
(2)水会不会溅出的实质是求点到距离时,点P是否在的下方,可作交于点,,可得到矩形、和,则可求,分别解这两个直角三角形即可。
(1)解:如图,过点E作,
∵,,
∴四边形是矩形,
∵,,
∴,,
∵,
∴,
∴;
(2)解:水不会溅出
由(1)可得,,,
在中,,
∴,
作交于点L,,
∵,,
∴,
∵在中,,
∴,
∴水不会溅出.
6.【答案】(1)解:在中,,,,
.
(2)解:解法一:在中,,,
.
,
.即.
解得.
答:广告牌低端顶点到地面的距离的长约为.
解法二:
在中,,,
.
在中,,,
,
.
答:广告牌低端顶点到地面的距离的长约为.
【解析】【分析】(1)在中运用正切解题即可;
(2)解法一:先在中根据正切得到,然后列方程解题即可;解法二:先在中得到,然后根据正切的定义求出h即可.
(1)解:在中,,,,
.
(2)解:解法一:在中,,,
.
,
.即.
解得.
答:广告牌低端顶点到地面的距离的长约为.
解法二:
在中,,,
.
在中,,,
,
.
答:广告牌低端顶点到地面的距离的长约为.
7.【答案】(1)解:过点作,垂足为,
,,
,
在中,,
,
,
,
端点距离地面的高度约为;
(2)解:过点作,交的延长线于点,过点作,垂足为,延长交于点,
由题意得:,,,
,
,
,
,
,
,
,
,
,
,
在中,,
答:的长约为.
【解析】【分析】(1)过点作,垂足为,由已知易得:,然后在中,根据锐角三角函数的定义cos∠ABC=求出的长,然后由线段的和差关系AE=AB-BE进行计算即可求解;
(2)过点作,交的延长线于点,过点作,垂足为,延长交于点,根据题意易得,在中,由含30度角的直角三角形的性质“30度角所对的直角边等于斜边的一半”可得BH=BC,然后由线段的和差关系FG=AH=AB-BH求出FG=AH的值,DG=DF-FG求出DG的值,由平角定义可得,然后在中,用锐角三角函数的定义sin∠DCG=即可求解.
8.【答案】(1)解:过点B作BE⊥AC于E,
∵OA=OC,∠AOC=120°,
∴∠OAC=∠OCA==30°,
∴h=BE=AB sin30°=110×=55;
(2)解:过点B作BE⊥AC于E,
∵OA=OC,∠AOC=74°,
∴∠OAC=∠OCA==53°,
∴AB=BE÷sin53°=120÷0.8=150(cm),
即该熨烫台支撑杆AB的长度约为150cm.
【解析】【分析】(1)先求出 ∠OAC=∠OCA==30°, 再求解即可;
(2)根据题意先求出 ∠OAC=∠OCA==53°, 再利用锐角三角函数计算求解即可。
9.【答案】(1)解:不赞同,理由如下:
连结OB,
由题知,,
则,
该物品不能顺利通过直角过道,
(2)解:如图,过点作PR的平行线,交过道两侧分别于点,由题可知,
,
,
,
,
(3)解:当时,物品能通过直角过道.
当,则,
同理,,
此时,,
所以物品的最大长度为米.
10.【答案】(1)解:设平移到,在地面上形成的影子为.
,
,,,
,,,
,
,
,
沿着方向平移时,长度不变.
(2)解:①以为圆心,长为半径画圆,
当与相切于时,此时最大为.
此时所在位置为.
②,,
,
,
设,则,
在中,
,
,
,
,(舍去),
,
由①,
,
,
即的长度的最大值为,
故答案为:80.
【解析】【分析】(1)设AB平移到EF,EF在地面上形成的影子为MN.根据平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似以及相似三角形的对应边之比相等,即可求解;
(2)①以A为圆心,AB长为半径画圆,当OQ与⊙A相切于H时,此时CD最大为CQ.
②根据有两组角对应相等的两个三角形相似得出△GHA∽△GPO,结合相似三角形的对应边之比相等和直角三角形中两直角边的平方和等于斜边的平方列出方程求出AG=30,由,即可求出CD的长度的最大值.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙江中考解答题专题——解直角三角形(含解析)
1.(2025·金华模拟)如图1,是一台小型输送机,其示意图如图2所示.已知两个支架的端点的距离,传输带与支架所成的角,支架端点离地面的高度,求支架端点离地面的高度.(结果精确到0.1m;参考数据,,).
2.(2024九下·南陵模拟)《海岛算经》是中国古代测量术的代表作,原名《重差》.这本著作建立起了从直接测量向间接测量的桥梁.直至近代,重差测量法仍有借鉴意义.
如图,为测量海岛上一座山峰的高度,直立两根高2米的标杆和,两杆间距相距6米,D、B、H三点共线.从点B处退行到点F,观察山顶A,发现A、C、F三点共线,且仰角为;从点D处退行到点G,观察山顶A,发现A、E、G三点共线,且仰角为.(点F、G都在直线上)
(1)求的长(结果保留根号);
(2)山峰高度的长(结果精确到米).
(参考数据:,)
3.(2025九下·奉化模拟)图1是某地下商业街的入口的玻璃顶,它是由立柱、斜杆、支撑杆组成的支架撑起的,图2是它的示意图.经过测量,支架的立柱与地面垂直,米,点在同一水平线上,斜杆与水平线的夹角,支撑杆,垂足为,该支架的边与的夹角,又测得米.
(1)求该支架的边的长;
(2)求支架的边的顶端到地面的距离.(结果精确到0.1米)(参考数据:)
4.(2024九下·杭州模拟)图1为科研小组研制的智能机器,水平操作台为l,底座AB固定,高为,始终与平台l垂直,连杆长度为,机械臂长度为,点B,C是转动点,与始终在同一平面内.
图1 图2
(1)转动连杆,机械臂,当张角且时(如图2),求机械臂臂端D到操作台l的距离.
(2)转动连杆,机械臂,要使机械臂端D能碰到操作台l上的物体M,则物体M离底座A的最远距离是多少?
5.(2024九下·浙江模拟)如图是水槽水龙头(图1)的侧面平面示意图,矩形为水槽侧面,有,在水槽边上方安装水管,水龙头,其中.测得,.
(1)求点F离水槽底的高度.
(2)若水柱与共线,当手伸到水槽内洗手时(即手与水柱的交点在下面),水不会溅出.当手与水柱交点P离水槽壁的距离为,洗手时水会不会溅出?试通过计算说明.(参考数据:)
6.(2025·绍兴模拟)综合与实践活动中,某数学兴趣小组利用所学的知识测量矩形广告牌的高度.
如图,在地面处测得广告牌顶端顶点的仰角为,走向广告牌到达处,在处测得广告牌低端顶点的仰角为,已知,立柱垂直于,且点,,在同一条水平直线上.(矩形广告牌与立柱垂直)过点作,垂足为.设(单位:).
(1)用含有和的式子表示线段的长;
(2)求广告牌低端顶点到地面的距离的长.(取,结果取整数)
7.(2024九下·柯桥模拟)随着时代的发展,手机“直播带货”已经成为当前最为强劲的购物新潮流.某种手机支架如图1所示,立杆垂直于地面,其高为,为支杆,它可绕点旋转,其中长为,为悬杆,滑动悬杆可调节的长度.(参考数据:,,)
(1)如图2,当、、三点共线,时,且支杆与立杆之间的夹角为,求端点距离地面的高度;
(2)调节支杆,悬杆,使得,,如图3所示,且点到地面的距离为,求的长.(结果精确到)
8.(2025九下·定海模拟)有一种升降熨烫台如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度.图2是这种升降熨烫台的平面示意图.AB和CD是两根相同长度的活动支撑杆,点O是它们的连接点,OA=OC,h(cm)表示熨烫台的高度.
(1)如图2﹣1.若AB=CD=110cm,∠AOC=120°,求h的值;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度为120cm时,两根支撑杆的夹角∠AOC是74°(如图2﹣2).求该熨烫台支撑杆AB的长度(结果精确到1cm).
(参考数据:sin37°≈0.6,cos37°≈0.8,sin53°≈0.8,cos53°≈0.6.)
9.(2025·萧山模拟)问题:如何将物品搬过直角过道
情景:图1是一直角过道示意图,O,P为直角顶点,过道宽度都是.矩形ABCD是某物品经过该过道时的俯视图,宽AB为.
操作:
步骤 动作 目标
1 靠边 将如图1中矩形ABCD的一边AD靠在SO上
2 推移 矩形ABCD沿SO方向推移一定距离,使点在边AD上
3 旋转 如图2,将矩形ABCD绕点旋转
4 推移 将矩形ABCD沿OT方向继续推移
探究:
(1)如图2,已知BC=1.6m,OD=0.6m.小明求得后,说:“,该物品能顺利通过直角过道.”你赞同小明的结论吗?请通过计算说明.
(2)如图3,物品转弯时被卡住(分别在墙面PQ与PR上),若.求OD的长.
(3)求该过道可以通过的物品最大长度,即求BC的最大值(精确到0.01米,).
10.(2024九下·杭州模拟)如图,玻璃桌面与地面平行、桌面上有一盏台灯和一支铅笔,点光源O与铅笔所确定的平面垂直于桌面.在灯光照射下,在地面上形成的影子为(不计折射),.
(1)在桌面上沿着方向平移铅笔,试说明的长度不变.
(2)桌面上一点P恰在点O的正下方,且,,,桌面的高度为.在点O与所确定的平面内,将绕点A旋转,使得的长度最大.
①画出此时所在位置的示意图;
②的长度的最大值为 cm.
答案解析部分
1.【答案】解:过点作于点,可得,在中,,
∴
∴
【解析】【分析】过点A作于点 F,可得CF长,然后在中根据余弦的定义求BF长解题即可.
2.【答案】(1)解:由题意得:,,
在中,,,
(米),
在中,,,
(米),
米,
米,
的长为米;
(2)解:设米,在中,,
(米),
∵米,
米,
在中,,
,
,
解得:,
米,
∴山峰高度的长约为米.
【解析】【分析】(1)根据题意得到,,然后在和中,利用解直角三角形求出和的长,解题即可;
(2)设米,在中,利用锐角三角函数的定义得到的长,从而表示长,再在中,利用解直角三角形可得,列方程解题即可.
3.【答案】(1)解:由题意得,,,
∴.
∵
∴.
∵,
∴,
∵
∴.
答:该支架的边的长7米.
(2)解:过点作,垂足为,过点作,垂足为G.则,
∵,
∴四边形是矩形,
∵,
∴.
∵,
∴.
∴,
∵,
∴.
答:支架的边的顶端到地面的距离为6.5米.
【解析】【分析】(1)先根据正弦的定义求出BC长,然后在Rt△BDE中利用余弦解题即可.
(2)过点作,垂足为,过点作,垂足为G.即可得到四边形是矩形,进而求出.然后根据正弦求出DG长解题即可.
(1)解:由题意得,,,
∴.
∵
∴.
∵,
∴,
∵
∴.
答:该支架的边的长7米.
(2)解:过点作,垂足为,过点作,垂足为G.
则,
∵,
∴四边形是矩形,
∵,
∴.
∵,
∴.
∴,
∵,
∴.
答:支架的边的顶端到地面的距离为6.5米.
4.【答案】(1)解:过点B作,垂足为F,延长交l于点E,如图,
则,
∵,
∴,
在中,,
∴,
∴,
∴,
∴机械臂臂端D到操作台l的距离为;
(2)解:当B、C、D三点共线时,此时M点与底座距离最远,如图:
∵,
∴,
在中,,
∴,
∴物体M离底座A的最远距离为.
【解析】【分析】(1)过点B作,垂足为F,根据题意可得,,从而可得,然后在中,利用锐角三角函数的定义sin∠CBF=求出的长,从而求出的长,然后根据线段的构成DE=CE-CD即可求解;
(2)当B、C、D三点共线时,此时M点与底座距离最远,由线段的构成BD=BC+CD求出BD的值,在Rt△ABD中,用勾股定理计算即可求解.
(1)解:过点B作,垂足为F,延长交l于点E,如图,
则,
∵,
∴,
在中,,
∴,
∴,
∴,
∴机械臂臂端D到操作台l的距离为;
(2)解:当B、C、D三点共线时,此时M点与底座距离最远,如图:
∵,
∴,
在中,,
∴,
∴物体M离底座A的最远距离为
5.【答案】(1)解:如图,过点E作,∵,,
∴四边形是矩形,
∵,,
∴,,
∵,
∴,
∴;
(2)解:水不会溅出由(1)可得,,,
在中,,
∴,
作交于点L,,
∵,,
∴,
∵在中,,
∴,
∴水不会溅出.
【解析】【分析】(1)要求FM的高度,可过点E作FM的垂线段AN,由矩形性质知,;由题意知,//,则与互补,又已知,解 求出即可;
(2)水会不会溅出的实质是求点到距离时,点P是否在的下方,可作交于点,,可得到矩形、和,则可求,分别解这两个直角三角形即可。
(1)解:如图,过点E作,
∵,,
∴四边形是矩形,
∵,,
∴,,
∵,
∴,
∴;
(2)解:水不会溅出
由(1)可得,,,
在中,,
∴,
作交于点L,,
∵,,
∴,
∵在中,,
∴,
∴水不会溅出.
6.【答案】(1)解:在中,,,,
.
(2)解:解法一:在中,,,
.
,
.即.
解得.
答:广告牌低端顶点到地面的距离的长约为.
解法二:
在中,,,
.
在中,,,
,
.
答:广告牌低端顶点到地面的距离的长约为.
【解析】【分析】(1)在中运用正切解题即可;
(2)解法一:先在中根据正切得到,然后列方程解题即可;解法二:先在中得到,然后根据正切的定义求出h即可.
(1)解:在中,,,,
.
(2)解:解法一:在中,,,
.
,
.即.
解得.
答:广告牌低端顶点到地面的距离的长约为.
解法二:
在中,,,
.
在中,,,
,
.
答:广告牌低端顶点到地面的距离的长约为.
7.【答案】(1)解:过点作,垂足为,
,,
,
在中,,
,
,
,
端点距离地面的高度约为;
(2)解:过点作,交的延长线于点,过点作,垂足为,延长交于点,
由题意得:,,,
,
,
,
,
,
,
,
,
,
,
在中,,
答:的长约为.
【解析】【分析】(1)过点作,垂足为,由已知易得:,然后在中,根据锐角三角函数的定义cos∠ABC=求出的长,然后由线段的和差关系AE=AB-BE进行计算即可求解;
(2)过点作,交的延长线于点,过点作,垂足为,延长交于点,根据题意易得,在中,由含30度角的直角三角形的性质“30度角所对的直角边等于斜边的一半”可得BH=BC,然后由线段的和差关系FG=AH=AB-BH求出FG=AH的值,DG=DF-FG求出DG的值,由平角定义可得,然后在中,用锐角三角函数的定义sin∠DCG=即可求解.
8.【答案】(1)解:过点B作BE⊥AC于E,
∵OA=OC,∠AOC=120°,
∴∠OAC=∠OCA==30°,
∴h=BE=AB sin30°=110×=55;
(2)解:过点B作BE⊥AC于E,
∵OA=OC,∠AOC=74°,
∴∠OAC=∠OCA==53°,
∴AB=BE÷sin53°=120÷0.8=150(cm),
即该熨烫台支撑杆AB的长度约为150cm.
【解析】【分析】(1)先求出 ∠OAC=∠OCA==30°, 再求解即可;
(2)根据题意先求出 ∠OAC=∠OCA==53°, 再利用锐角三角函数计算求解即可。
9.【答案】(1)解:不赞同,理由如下:
连结OB,
由题知,,
则,
该物品不能顺利通过直角过道,
(2)解:如图,过点作PR的平行线,交过道两侧分别于点,由题可知,
,
,
,
,
(3)解:当时,物品能通过直角过道.
当,则,
同理,,
此时,,
所以物品的最大长度为米.
10.【答案】(1)解:设平移到,在地面上形成的影子为.
,
,,,
,,,
,
,
,
沿着方向平移时,长度不变.
(2)解:①以为圆心,长为半径画圆,
当与相切于时,此时最大为.
此时所在位置为.
②,,
,
,
设,则,
在中,
,
,
,
,(舍去),
,
由①,
,
,
即的长度的最大值为,
故答案为:80.
【解析】【分析】(1)设AB平移到EF,EF在地面上形成的影子为MN.根据平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似以及相似三角形的对应边之比相等,即可求解;
(2)①以A为圆心,AB长为半径画圆,当OQ与⊙A相切于H时,此时CD最大为CQ.
②根据有两组角对应相等的两个三角形相似得出△GHA∽△GPO,结合相似三角形的对应边之比相等和直角三角形中两直角边的平方和等于斜边的平方列出方程求出AG=30,由,即可求出CD的长度的最大值.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
