浙江2025年中考解答题专题——一次函数反比例函数(含解析)
文档属性
| 名称 | 浙江2025年中考解答题专题——一次函数反比例函数(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙江中考解答题专题——一次函数反比例函数(含解析)
一、解答题:
1.(2025·绍兴模拟)已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程 与时间 的函数关系的图象,根据图象解答下列问题.
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?
2.(2025·浙江模拟)在一条笔直的公路上依次有A,B,C三地,小明、小红两人同时出发,小明从B地骑自行车匀速去A地拿东西,停留一段时间后,再以相同的速度匀速前往C地,小红步行匀速从C地至A地,小明、小红两人距C地的距离y(米)与时间x(分)之间的函数关系如图所示,请结合图象解答下列问题:
(1)求小明、小红两人的速度.
(2)求小明从A地前往C地过程中y关于x的函数表达式.
(3)请求出经过多少时间后,小明与小红相距600米.
3.(2024九下·乐清模拟)小乐和小嘉同时从学校出发,分别骑自行车沿同一条路线到体育馆进行锻炼,图中折线和线段OD分别表示小乐和小嘉离学校的距离y(米)与时间x(分钟)的函数关系的图象,且两人骑车速度均保持不变,根据图中信息,解答下列问题:
(1)求出小嘉离学校的距离y(米)与时间x(分钟)的函数表达式,并直接写出图中a的值.
(2)出发后经过15分钟,小乐和小嘉相距多少米?
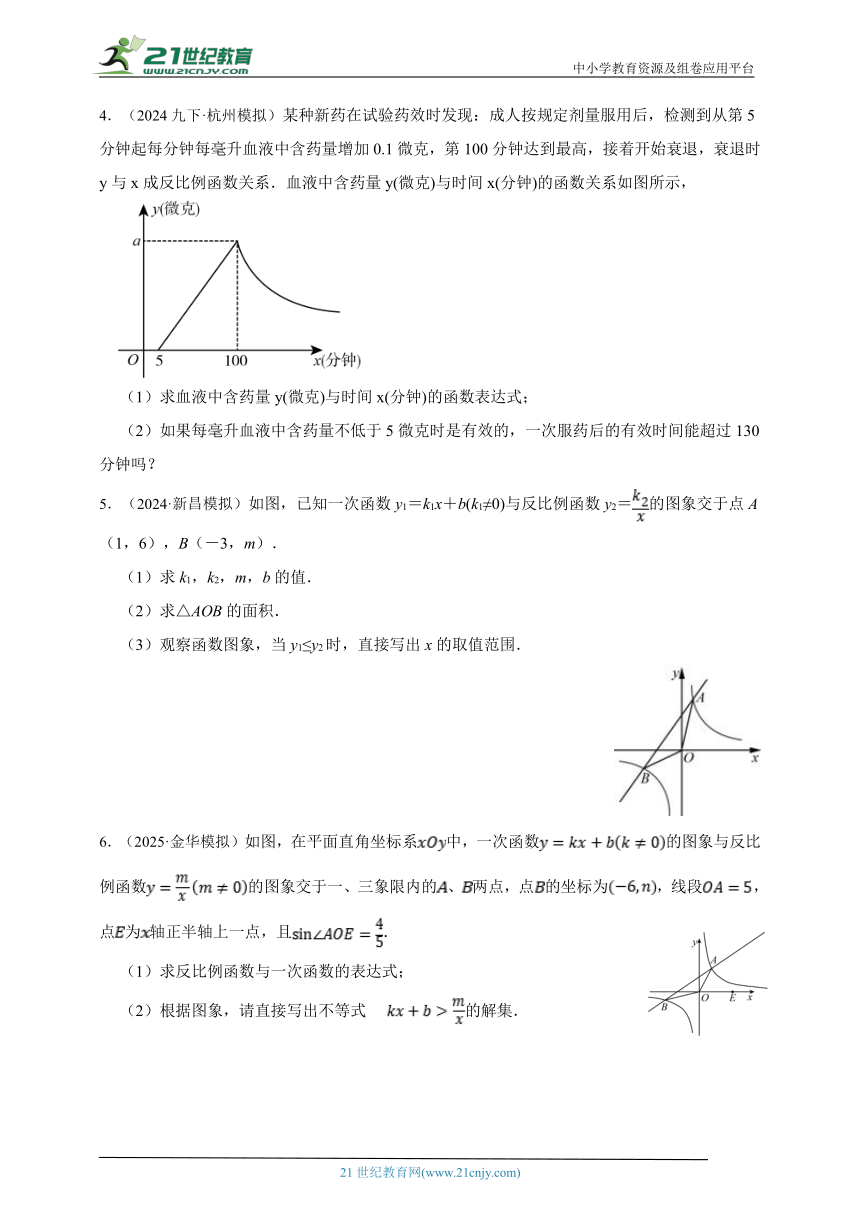
4.(2024九下·杭州模拟)某种新药在试验药效时发现:成人按规定剂量服用后,检测到从第5分钟起每分钟每毫升血液中含药量增加0.1微克,第100分钟达到最高,接着开始衰退,衰退时y与x成反比例函数关系.血液中含药量y(微克)与时间x(分钟)的函数关系如图所示,
(1)求血液中含药量y(微克)与时间x(分钟)的函数表达式;
(2)如果每毫升血液中含药量不低于5微克时是有效的,一次服药后的有效时间能超过130分钟吗?
5.(2024·新昌模拟)如图,已知一次函数y1=k1x+b(k1≠0)与反比例函数y2=的图象交于点A(1,6),B(-3,m).
(1)求k1,k2,m,b的值.
(2)求△AOB的面积.
(3)观察函数图象,当y1≤y2时,直接写出x的取值范围.
6.(2025·金华模拟)如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于一、三象限内的、两点,点的坐标为,线段,点为轴正半轴上一点,且.
(1)求反比例函数与一次函数的表达式;
(2)根据图象,请直接写出不等式的解集.
7.(2025·萧山模拟)【背景】在一次物理实验中,小冉同学用一个固定电压为12V的蓄电池,通过调节滑动变阻器来改变电流大小,完成控制灯泡L(灯丝的阻值RL=2Ω)亮度的实验(如图),已知串联电路中,电流与电阻R,RL之间关系为,通过实验得出如下数据:
R(Ω) … 1 a 3 4 6 …
I(A) … 4 3 2.4 2 b …
(1)a= ,b= .
(2)【探究】根据以上实验,构建出函数,结合表格信息,探究函数的图象与性质.
①在平面直角坐标系中画出对应函数的图象.
②随着自变量的不断增大,函数值的变化趋势是 ▲ .
(3)【拓展】结合(2)中函数图象分析,当0时,的解为 .
8.(2025·鄞州模拟)如图,一次函数的图象与反比例函数的图象相交于两点.
(1)求一次函数和反比例函数的表达式;
(2)根据图象直接写出时,的取值范围;
(3)过点作直线,交反比例函数图象于点,连结,求的面积.
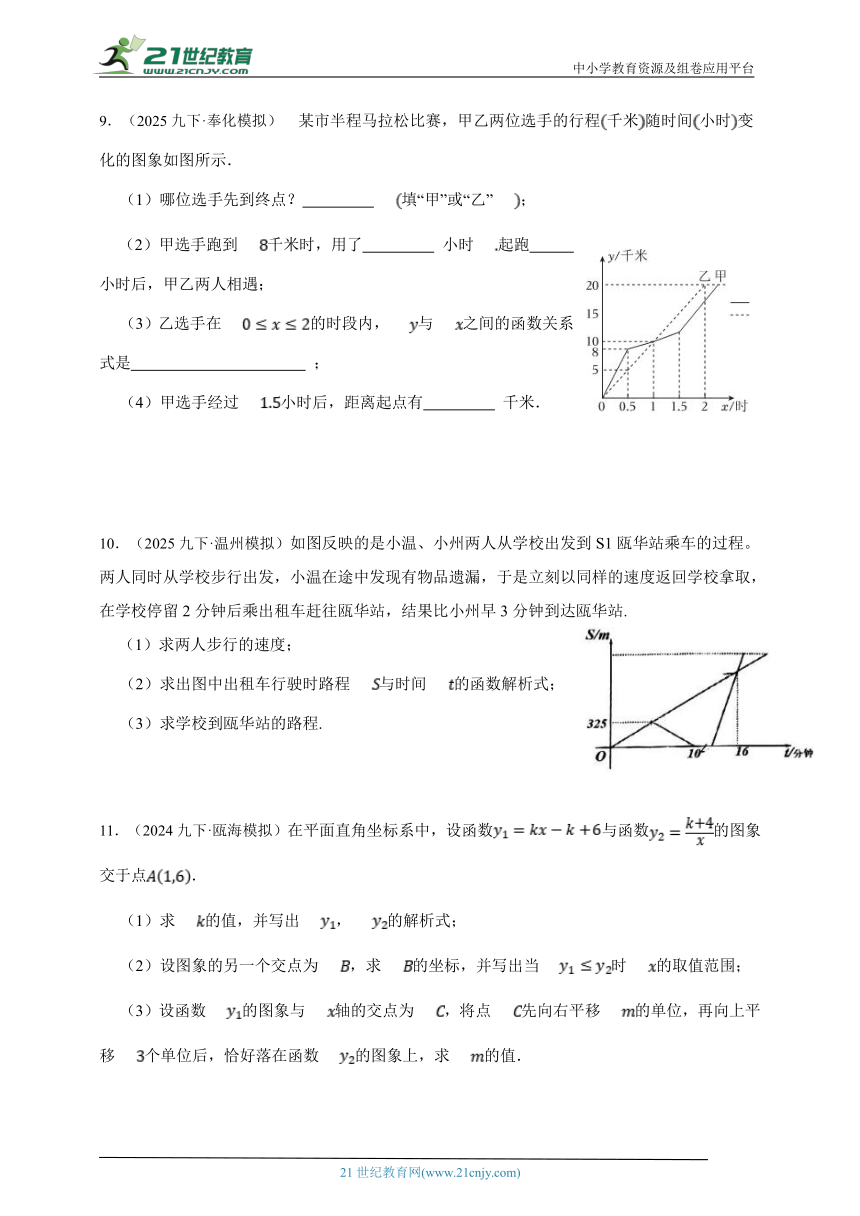
9.(2025九下·奉化模拟) 某市半程马拉松比赛,甲乙两位选手的行程千米随时间小时变化的图象如图所示.
(1)哪位选手先到终点? 填“甲”或“乙”;
(2)甲选手跑到千米时,用了 小时起跑 小时后,甲乙两人相遇;
(3)乙选手在的时段内,与之间的函数关系式是 ;
(4)甲选手经过小时后,距离起点有 千米.
10.(2025九下·温州模拟)如图反映的是小温、小州两人从学校出发到S1瓯华站乘车的过程。两人同时从学校步行出发,小温在途中发现有物品遗漏,于是立刻以同样的速度返回学校拿取,在学校停留2分钟后乘出租车赶往瓯华站,结果比小州早3分钟到达瓯华站.
(1)求两人步行的速度;
(2)求出图中出租车行驶时路程与时间的函数解析式;
(3)求学校到瓯华站的路程.
11.(2024九下·瓯海模拟)在平面直角坐标系中,设函数与函数的图象交于点.
(1)求的值,并写出,的解析式;
(2)设图象的另一个交点为,求的坐标,并写出当时的取值范围;
(3)设函数的图象与轴的交点为,将点先向右平移的单位,再向上平移个单位后,恰好落在函数的图象上,求的值.
12.(2024九下·浙江模拟)如图所示,直线与双曲线交于,两点,与轴交于点.
(1)求的值;
(2)求的面积;
(3)请结合上述两个函数的图象,请直接写出的解集.
答案解析部分
1.【答案】(1)解:由图可知,A比B后出发1小时;
B的速度:
(2)解:由图可知点 , , ,
设OC的解析式为 ,
则 ,
解得 ,
所以, ,
设DE的解析式为 ,
则 ,
解得 ,
所以, ,
由题意得 ,
解得 ,
所以,B出发 小时后两人相遇
【解析】【分析】(1)由图中的信息可知, A比B后出发1小时; B的速度=B走的路程时间可求解;
(2) 由图可知点 , , ,用待定系数法 可求得直线OC和直线DE的解析式,再将两条直线的解析式联立解方程组,即可求得两人相遇的时间。
2.【答案】(1)解:小明骑自行车速度是:(1200-400)÷2=400(米/分)
小红步行速度是:1200÷12=100(米/分)
(2)解:小明从A地骑自行车到C地的时间为1200÷400=3(分)
将(9,1200),(12,0)代入y=kx+b
得
y=-400x+4800
(3)解: 情况一:小明从A地到C地的途中,两人相距600米;此时,小明行驶的路程为400x+400,小红行驶的路程为100x ,
根据题意,得,解得;
情况二:小明到达C地后,两人相距600米;此时,小明到达C地,小红行驶的路程为100x,
根据题意,得,解得x=6;
情况三:小明到达C地后,小红超过小明600米;此时,小明到达C地,小红行驶的路程为100x,
根据题意,得 ,解得 ,
答:经过或6或分钟后,小明与小红相距600米 .
【解析】【分析】(1)由图象可得小明从B地到A地, 停留一段时间后,再以相同的速度匀速从A地到C地,行驶的路程为(1200-400)米时,用时2分钟;小红从A地到C地,行驶的路程是1200米,用时12分钟,从而根据速度等于路程除以时间,列式计算即可;
(2)小明从A地到C地的过程是一条直线,因此y关于x的函数关系式为一次函数,根据图象,我们可以得到该段直线上两个坐标点(9,1200)和(12,0),从而利用待定系数法求解即可;
(3)分类讨论:①小明从A地到C地的途中,两人相距600米;②小明到达C地后,两人相距600米;③小明到达C地后,小红超过小明600米,分别列出方程,求解即可.
3.【答案】(1)解:设小嘉离学校的距离(米与时间(分钟)的函数表达式为,
把代入解析式得:,
解得,
小嘉离学校的距离(米与时间(分钟)的函数表达式为;
由图象知,小乐的速度为(米分),
小乐重新出发到到达体育馆所用时间为(分钟),
;
(2)解:(米),
答:出发后经过15分钟,小乐和小嘉相距900米.
【解析】【分析】本题主要考查了一次函数的应用,正确理解图象是解题关键.
(1)观察图象知,表示小嘉同学路程与时间的函数是正比例函数,因此可利用其图象上的点(6,1200)直接使用待定系数法即可;
(2)观察图象知,小乐有一段停留时间,但由于小乐停留前后的速度保先不变,因此可先利用前1200米所用的时间4求出其速度,再用速度与后面的路程求出行走时间从而得到a的值,再利用待定系数法求出其后一段路程与时间的函数关系式,进而可求出15分钟后两人的距离.
4.【答案】(1)解:从第5分钟起每分钟每毫升血液中含药量增加0.1微克,
∴,
当时,设y与x之间的函数关系式为,
∵经过点,
∴,
解得,
∴;
当时,y与x之间的函数关系式为,
∵经过点,
∴,
解得,即;
(2)解:令,解得,
令,
解得,
∴一次服药后的有效视角为:(分钟),超过分钟.
【解析】【分析】(1)运用待定系数法求函数解析式即可;
(2)把代入一次函数,反比例函数求出时间,然后求差解题.
(1)解:从第5分钟起每分钟每毫升血液中含药量增加0.1微克,
∴,
当时,设y与x之间的函数关系式为,
∵经过点,
∴,
解得,
∴;
当时,y与x之间的函数关系式为,
∵经过点,
∴,
解得,即;
(2)解:令,
解得,
令,
解得,
∴一次服药后的有效视角为:(分钟),超过分钟.
5.【答案】(1)解:由题意,得
k2=6,m=-2.
将点A(1,6),B(-3,-2)代入y1=k1x+b,得
解得k1=2,b=4.
(2)解:因为y1=2x+4,
所以直线与y轴的交点为(0,4).
所以△AOB的面积=×4×4=8.
(3)解:当y1≤y2时,
x的取值范围是x≤-3或0<x≤1.
【解析】【分析】(1)根据反比例函数图象上点的坐标特征求出k2=6,m=-2,再利用待定系数法求出一次函数解析式即可;
(2)先求出直线y1=2x+4与y轴的交点为(0,4),利用三角形的面积公式计算即可.
(3)根据图象知:当x≤-3或0<x≤1,直线y1的图象在反比例函数y2图象的上方,继而得解 .
6.【答案】(1)解:
如图所示,过点A作 轴于点F,
∴在 中,
∴A(3,4),
∵点A(3,4)在反比例函数 的图象上,
∴反比例函数解析式为
∵点 在反比例函数图象上,
即
把点A(3,4), 代入一次函数得:
解得,
∴一次函数的解析式为
(2)解:已知点A(3,4), 点 结合图象可得,当 时, 当 时,
∴解集为: 或
【解析】【分析】(1)如图所示,过点A作. 轴于点F,根据可求出点A的坐标,由此可求出反比例函数解析式,再把点B的坐标代入,可求出点B的坐标,运用待定系数法可求出一次函数解析式;
(2)根据点A,B的坐标,图形结合即可求解.
7.【答案】(1)2;1.5
(2)解:①根据表格数据描点:,,,,,在平面直角坐标系中画出对应函数的图象如下:
②不断减小
(3)或
【解析】【解答】(1)根据题意,
故答案为: 2, 1.5;
(2)②由图象可知,随着自变量x的不断增大,函数值y的变化趋势是不断减小,
故答案为:不断减小;
(3)如图:
由函数图象知, 当 或 时,
即当 时,
故答案为: 或
【解答】(1)由已知列出方程,即可解得a,b的值;
(2)①描点画出图象即可;
②观察图象可得答案;
(3)同一坐标系内画出图象,观察即可得到答案.
8.【答案】(1)解: 将点A坐标代入反比例函数解析式得,
所以反比例函数解析式为
将点B坐标代入反比例函数解析式得,
所以点B的坐标为(
将A,B两点坐标代入一次函数解析式得,
解得
所以一次函数解析式为
(2)解:由函数图象可知,当 或 时,一次函数的图象在反比例函数图象的上方,即
所以当 x的取值范围是: 或
(3)解:连接AO,令直线AB与x轴的交点为M,
将 代入 得,
所以点M的坐标为(
所以
因为正比例函数图象与反比例函数图象都是中心对
称图形,且坐标原点是对称中心,
所以点B和点C关于点O成中心对称,
所以
所以
【解析】【分析】(1)先将点A坐标代入反比例函数解析式,求出m,再求出点B坐标,最后用待定系数法求出一次函数解析式即可.
(2)利用数形结合的数学思想即可解决问题.
(3)连接AO,根据反比例函数与正比例函数的对称性,将 的面积转化为 面积的2倍即可解决问题.
9.【答案】(1)乙
(2)0.5;1
(3);
(4)12
【解析】【解答】解:(1)由图可知,乙选手先到终点,
故答案为:乙;
(2)由图可知,甲选手跑到8千米时,用了0.5小时,起跑1小时后,甲乙两人相遇,
故答案为: 0.5, 1;
(3)由图可得,乙选手的速度为 (千米/小时) ,
∴y与x之间的函数关系式 是 ;
故答案为:
(4)由图可知,甲0.5小时距离起点8千米,1小时距离起点10千米,
时, 甲用0.5小时跑了 (千米),
时,甲距离起点 (千米),
故答案为: 12.
【分析】(1)观察图象直接可得答案;
(2)观察图象直接可得答案;
(3)求出乙的速度,即可得到y与x之间的函数关系式;
(4)由图象知: 时,甲用0.5小时跑了2千米,即可得到答案.
10.【答案】(1)解:步行速度(分钟);
(2)解:如图所示
由题可知当时,,所以点;
当时,,所以点;
设函数解析式为,
,解得
(3)解:设学校到瓯华站共米,由题意列方程得:
,解得
答: 学校到瓯华站的路程为
【解析】【分析】(1)由于小温出发和返回学校的速度相同,则从学校到返回地点用时为10分钟的一半即5分钟,步行路程为325,则速度等于路程除以时间即可;
(2)求出租车的路程与时间的函数解析式,由题意可分别求出A、B两点的坐标,再利用待定系数法联立方程组即可;
(3)求学校到车站的路程,由于相遇后出租车比小州早到3分钟,即在走完剩余路程中,出租车用时比小州少了3分钟,由于小州的速度已知为65,出租车的速度利用函数关系式知为260,剩余路程为总路程减去小州步行16分钟的路程1040,列方程即可求出总路程。
11.【答案】(1)解:将点代入函数 中,得:,
解得:k=2,
将k=2代入 函数 ,得:,
将k=2代入 函数 ,得:,
答:函数,函数;
(2)解:将函数与函数联立方程组,得:;
解这个方程组,得:或,
∴ 图象的另一个交点为(-3,-2),
根据函数图象可知,当时,的取值范围为或;
(3)解:函数y1得表达式为,
∴ 函数的图象与轴的交点为(-2,0),
∴ 将点先向右平移的单位,再向上平移个单位后,点C的坐标为(-2+m,3) ,
∵ 点C恰好落在函数的图象上,
∴3=,
解得:m=4.
答:的值是4.
【解析】【分析】()先将点代入入函数 即可求出,再将k代入函数,即可确定两个函数的解析式;
()将函数 与函数联立,列出方程组,即可求出的坐标,再根据函数图象即可求出当时的取值范围;
()先根据点C恰好落在函数的图象上求出的坐标,进而表示出平移后的解析式,代入反比例函数解析式求出即可.
(1)把点代入中,得,
解得,
∴函数,函数;
(2)联立解析式得,
解得:或,
∴,
∴当时,的取值范围为或;
(3)当时,,解得,
∴,
∵点先向右平移的单位,再向上平移个单位,
∴平移后的坐标为,
∴代入反比例函数解析式得,
解得:.
12.【答案】(1)解:根据题意可知,直线经过点A(2,n),
∴,
∴点A的坐标为(2,3),
又∵ 双曲线 也经过点A,
∴3=,
∴k=6
答:k的值为6,n的值为3.
(2)解:令直线与x轴的交点为E,如图所示:
将直线 与双曲线联立方程组,得:
,
解得:或,
∴点B(6,1),
将x=0代入得:y=4,
∴点D(0,4),
将y=0代入得:x=8,
∴点E(8,0),
∴S△AOB=S△DOE-S△DOA-S△BOE==8.
(3)解:将不等式 变形为,
根据函数图象可知:
当0<x<2,或者x>6时,,
∴的解集为或.
【解析】【分析】(1)先将点代入直线求得点,再将点代入即可求出的值;
(2)令直线与x轴的交点为E,根据函数解析式分别求出点D、B、E的坐标,再根据S△AOB=S△DOE-S△DOA-S△BOE即可可得结论.
(3)根据图象直接判断不等式的解集即可.
(1)将点代入 得,
,
将代入,
;
(2)令 中,得,
,
解方程组,
得或,
,
;
(3)即为,
根据图象得或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙江中考解答题专题——一次函数反比例函数(含解析)
一、解答题:
1.(2025·绍兴模拟)已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程 与时间 的函数关系的图象,根据图象解答下列问题.
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?
2.(2025·浙江模拟)在一条笔直的公路上依次有A,B,C三地,小明、小红两人同时出发,小明从B地骑自行车匀速去A地拿东西,停留一段时间后,再以相同的速度匀速前往C地,小红步行匀速从C地至A地,小明、小红两人距C地的距离y(米)与时间x(分)之间的函数关系如图所示,请结合图象解答下列问题:
(1)求小明、小红两人的速度.
(2)求小明从A地前往C地过程中y关于x的函数表达式.
(3)请求出经过多少时间后,小明与小红相距600米.
3.(2024九下·乐清模拟)小乐和小嘉同时从学校出发,分别骑自行车沿同一条路线到体育馆进行锻炼,图中折线和线段OD分别表示小乐和小嘉离学校的距离y(米)与时间x(分钟)的函数关系的图象,且两人骑车速度均保持不变,根据图中信息,解答下列问题:
(1)求出小嘉离学校的距离y(米)与时间x(分钟)的函数表达式,并直接写出图中a的值.
(2)出发后经过15分钟,小乐和小嘉相距多少米?
4.(2024九下·杭州模拟)某种新药在试验药效时发现:成人按规定剂量服用后,检测到从第5分钟起每分钟每毫升血液中含药量增加0.1微克,第100分钟达到最高,接着开始衰退,衰退时y与x成反比例函数关系.血液中含药量y(微克)与时间x(分钟)的函数关系如图所示,
(1)求血液中含药量y(微克)与时间x(分钟)的函数表达式;
(2)如果每毫升血液中含药量不低于5微克时是有效的,一次服药后的有效时间能超过130分钟吗?
5.(2024·新昌模拟)如图,已知一次函数y1=k1x+b(k1≠0)与反比例函数y2=的图象交于点A(1,6),B(-3,m).
(1)求k1,k2,m,b的值.
(2)求△AOB的面积.
(3)观察函数图象,当y1≤y2时,直接写出x的取值范围.
6.(2025·金华模拟)如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于一、三象限内的、两点,点的坐标为,线段,点为轴正半轴上一点,且.
(1)求反比例函数与一次函数的表达式;
(2)根据图象,请直接写出不等式的解集.
7.(2025·萧山模拟)【背景】在一次物理实验中,小冉同学用一个固定电压为12V的蓄电池,通过调节滑动变阻器来改变电流大小,完成控制灯泡L(灯丝的阻值RL=2Ω)亮度的实验(如图),已知串联电路中,电流与电阻R,RL之间关系为,通过实验得出如下数据:
R(Ω) … 1 a 3 4 6 …
I(A) … 4 3 2.4 2 b …
(1)a= ,b= .
(2)【探究】根据以上实验,构建出函数,结合表格信息,探究函数的图象与性质.
①在平面直角坐标系中画出对应函数的图象.
②随着自变量的不断增大,函数值的变化趋势是 ▲ .
(3)【拓展】结合(2)中函数图象分析,当0时,的解为 .
8.(2025·鄞州模拟)如图,一次函数的图象与反比例函数的图象相交于两点.
(1)求一次函数和反比例函数的表达式;
(2)根据图象直接写出时,的取值范围;
(3)过点作直线,交反比例函数图象于点,连结,求的面积.
9.(2025九下·奉化模拟) 某市半程马拉松比赛,甲乙两位选手的行程千米随时间小时变化的图象如图所示.
(1)哪位选手先到终点? 填“甲”或“乙”;
(2)甲选手跑到千米时,用了 小时起跑 小时后,甲乙两人相遇;
(3)乙选手在的时段内,与之间的函数关系式是 ;
(4)甲选手经过小时后,距离起点有 千米.
10.(2025九下·温州模拟)如图反映的是小温、小州两人从学校出发到S1瓯华站乘车的过程。两人同时从学校步行出发,小温在途中发现有物品遗漏,于是立刻以同样的速度返回学校拿取,在学校停留2分钟后乘出租车赶往瓯华站,结果比小州早3分钟到达瓯华站.
(1)求两人步行的速度;
(2)求出图中出租车行驶时路程与时间的函数解析式;
(3)求学校到瓯华站的路程.
11.(2024九下·瓯海模拟)在平面直角坐标系中,设函数与函数的图象交于点.
(1)求的值,并写出,的解析式;
(2)设图象的另一个交点为,求的坐标,并写出当时的取值范围;
(3)设函数的图象与轴的交点为,将点先向右平移的单位,再向上平移个单位后,恰好落在函数的图象上,求的值.
12.(2024九下·浙江模拟)如图所示,直线与双曲线交于,两点,与轴交于点.
(1)求的值;
(2)求的面积;
(3)请结合上述两个函数的图象,请直接写出的解集.
答案解析部分
1.【答案】(1)解:由图可知,A比B后出发1小时;
B的速度:
(2)解:由图可知点 , , ,
设OC的解析式为 ,
则 ,
解得 ,
所以, ,
设DE的解析式为 ,
则 ,
解得 ,
所以, ,
由题意得 ,
解得 ,
所以,B出发 小时后两人相遇
【解析】【分析】(1)由图中的信息可知, A比B后出发1小时; B的速度=B走的路程时间可求解;
(2) 由图可知点 , , ,用待定系数法 可求得直线OC和直线DE的解析式,再将两条直线的解析式联立解方程组,即可求得两人相遇的时间。
2.【答案】(1)解:小明骑自行车速度是:(1200-400)÷2=400(米/分)
小红步行速度是:1200÷12=100(米/分)
(2)解:小明从A地骑自行车到C地的时间为1200÷400=3(分)
将(9,1200),(12,0)代入y=kx+b
得
y=-400x+4800
(3)解: 情况一:小明从A地到C地的途中,两人相距600米;此时,小明行驶的路程为400x+400,小红行驶的路程为100x ,
根据题意,得,解得;
情况二:小明到达C地后,两人相距600米;此时,小明到达C地,小红行驶的路程为100x,
根据题意,得,解得x=6;
情况三:小明到达C地后,小红超过小明600米;此时,小明到达C地,小红行驶的路程为100x,
根据题意,得 ,解得 ,
答:经过或6或分钟后,小明与小红相距600米 .
【解析】【分析】(1)由图象可得小明从B地到A地, 停留一段时间后,再以相同的速度匀速从A地到C地,行驶的路程为(1200-400)米时,用时2分钟;小红从A地到C地,行驶的路程是1200米,用时12分钟,从而根据速度等于路程除以时间,列式计算即可;
(2)小明从A地到C地的过程是一条直线,因此y关于x的函数关系式为一次函数,根据图象,我们可以得到该段直线上两个坐标点(9,1200)和(12,0),从而利用待定系数法求解即可;
(3)分类讨论:①小明从A地到C地的途中,两人相距600米;②小明到达C地后,两人相距600米;③小明到达C地后,小红超过小明600米,分别列出方程,求解即可.
3.【答案】(1)解:设小嘉离学校的距离(米与时间(分钟)的函数表达式为,
把代入解析式得:,
解得,
小嘉离学校的距离(米与时间(分钟)的函数表达式为;
由图象知,小乐的速度为(米分),
小乐重新出发到到达体育馆所用时间为(分钟),
;
(2)解:(米),
答:出发后经过15分钟,小乐和小嘉相距900米.
【解析】【分析】本题主要考查了一次函数的应用,正确理解图象是解题关键.
(1)观察图象知,表示小嘉同学路程与时间的函数是正比例函数,因此可利用其图象上的点(6,1200)直接使用待定系数法即可;
(2)观察图象知,小乐有一段停留时间,但由于小乐停留前后的速度保先不变,因此可先利用前1200米所用的时间4求出其速度,再用速度与后面的路程求出行走时间从而得到a的值,再利用待定系数法求出其后一段路程与时间的函数关系式,进而可求出15分钟后两人的距离.
4.【答案】(1)解:从第5分钟起每分钟每毫升血液中含药量增加0.1微克,
∴,
当时,设y与x之间的函数关系式为,
∵经过点,
∴,
解得,
∴;
当时,y与x之间的函数关系式为,
∵经过点,
∴,
解得,即;
(2)解:令,解得,
令,
解得,
∴一次服药后的有效视角为:(分钟),超过分钟.
【解析】【分析】(1)运用待定系数法求函数解析式即可;
(2)把代入一次函数,反比例函数求出时间,然后求差解题.
(1)解:从第5分钟起每分钟每毫升血液中含药量增加0.1微克,
∴,
当时,设y与x之间的函数关系式为,
∵经过点,
∴,
解得,
∴;
当时,y与x之间的函数关系式为,
∵经过点,
∴,
解得,即;
(2)解:令,
解得,
令,
解得,
∴一次服药后的有效视角为:(分钟),超过分钟.
5.【答案】(1)解:由题意,得
k2=6,m=-2.
将点A(1,6),B(-3,-2)代入y1=k1x+b,得
解得k1=2,b=4.
(2)解:因为y1=2x+4,
所以直线与y轴的交点为(0,4).
所以△AOB的面积=×4×4=8.
(3)解:当y1≤y2时,
x的取值范围是x≤-3或0<x≤1.
【解析】【分析】(1)根据反比例函数图象上点的坐标特征求出k2=6,m=-2,再利用待定系数法求出一次函数解析式即可;
(2)先求出直线y1=2x+4与y轴的交点为(0,4),利用三角形的面积公式计算即可.
(3)根据图象知:当x≤-3或0<x≤1,直线y1的图象在反比例函数y2图象的上方,继而得解 .
6.【答案】(1)解:
如图所示,过点A作 轴于点F,
∴在 中,
∴A(3,4),
∵点A(3,4)在反比例函数 的图象上,
∴反比例函数解析式为
∵点 在反比例函数图象上,
即
把点A(3,4), 代入一次函数得:
解得,
∴一次函数的解析式为
(2)解:已知点A(3,4), 点 结合图象可得,当 时, 当 时,
∴解集为: 或
【解析】【分析】(1)如图所示,过点A作. 轴于点F,根据可求出点A的坐标,由此可求出反比例函数解析式,再把点B的坐标代入,可求出点B的坐标,运用待定系数法可求出一次函数解析式;
(2)根据点A,B的坐标,图形结合即可求解.
7.【答案】(1)2;1.5
(2)解:①根据表格数据描点:,,,,,在平面直角坐标系中画出对应函数的图象如下:
②不断减小
(3)或
【解析】【解答】(1)根据题意,
故答案为: 2, 1.5;
(2)②由图象可知,随着自变量x的不断增大,函数值y的变化趋势是不断减小,
故答案为:不断减小;
(3)如图:
由函数图象知, 当 或 时,
即当 时,
故答案为: 或
【解答】(1)由已知列出方程,即可解得a,b的值;
(2)①描点画出图象即可;
②观察图象可得答案;
(3)同一坐标系内画出图象,观察即可得到答案.
8.【答案】(1)解: 将点A坐标代入反比例函数解析式得,
所以反比例函数解析式为
将点B坐标代入反比例函数解析式得,
所以点B的坐标为(
将A,B两点坐标代入一次函数解析式得,
解得
所以一次函数解析式为
(2)解:由函数图象可知,当 或 时,一次函数的图象在反比例函数图象的上方,即
所以当 x的取值范围是: 或
(3)解:连接AO,令直线AB与x轴的交点为M,
将 代入 得,
所以点M的坐标为(
所以
因为正比例函数图象与反比例函数图象都是中心对
称图形,且坐标原点是对称中心,
所以点B和点C关于点O成中心对称,
所以
所以
【解析】【分析】(1)先将点A坐标代入反比例函数解析式,求出m,再求出点B坐标,最后用待定系数法求出一次函数解析式即可.
(2)利用数形结合的数学思想即可解决问题.
(3)连接AO,根据反比例函数与正比例函数的对称性,将 的面积转化为 面积的2倍即可解决问题.
9.【答案】(1)乙
(2)0.5;1
(3);
(4)12
【解析】【解答】解:(1)由图可知,乙选手先到终点,
故答案为:乙;
(2)由图可知,甲选手跑到8千米时,用了0.5小时,起跑1小时后,甲乙两人相遇,
故答案为: 0.5, 1;
(3)由图可得,乙选手的速度为 (千米/小时) ,
∴y与x之间的函数关系式 是 ;
故答案为:
(4)由图可知,甲0.5小时距离起点8千米,1小时距离起点10千米,
时, 甲用0.5小时跑了 (千米),
时,甲距离起点 (千米),
故答案为: 12.
【分析】(1)观察图象直接可得答案;
(2)观察图象直接可得答案;
(3)求出乙的速度,即可得到y与x之间的函数关系式;
(4)由图象知: 时,甲用0.5小时跑了2千米,即可得到答案.
10.【答案】(1)解:步行速度(分钟);
(2)解:如图所示
由题可知当时,,所以点;
当时,,所以点;
设函数解析式为,
,解得
(3)解:设学校到瓯华站共米,由题意列方程得:
,解得
答: 学校到瓯华站的路程为
【解析】【分析】(1)由于小温出发和返回学校的速度相同,则从学校到返回地点用时为10分钟的一半即5分钟,步行路程为325,则速度等于路程除以时间即可;
(2)求出租车的路程与时间的函数解析式,由题意可分别求出A、B两点的坐标,再利用待定系数法联立方程组即可;
(3)求学校到车站的路程,由于相遇后出租车比小州早到3分钟,即在走完剩余路程中,出租车用时比小州少了3分钟,由于小州的速度已知为65,出租车的速度利用函数关系式知为260,剩余路程为总路程减去小州步行16分钟的路程1040,列方程即可求出总路程。
11.【答案】(1)解:将点代入函数 中,得:,
解得:k=2,
将k=2代入 函数 ,得:,
将k=2代入 函数 ,得:,
答:函数,函数;
(2)解:将函数与函数联立方程组,得:;
解这个方程组,得:或,
∴ 图象的另一个交点为(-3,-2),
根据函数图象可知,当时,的取值范围为或;
(3)解:函数y1得表达式为,
∴ 函数的图象与轴的交点为(-2,0),
∴ 将点先向右平移的单位,再向上平移个单位后,点C的坐标为(-2+m,3) ,
∵ 点C恰好落在函数的图象上,
∴3=,
解得:m=4.
答:的值是4.
【解析】【分析】()先将点代入入函数 即可求出,再将k代入函数,即可确定两个函数的解析式;
()将函数 与函数联立,列出方程组,即可求出的坐标,再根据函数图象即可求出当时的取值范围;
()先根据点C恰好落在函数的图象上求出的坐标,进而表示出平移后的解析式,代入反比例函数解析式求出即可.
(1)把点代入中,得,
解得,
∴函数,函数;
(2)联立解析式得,
解得:或,
∴,
∴当时,的取值范围为或;
(3)当时,,解得,
∴,
∵点先向右平移的单位,再向上平移个单位,
∴平移后的坐标为,
∴代入反比例函数解析式得,
解得:.
12.【答案】(1)解:根据题意可知,直线经过点A(2,n),
∴,
∴点A的坐标为(2,3),
又∵ 双曲线 也经过点A,
∴3=,
∴k=6
答:k的值为6,n的值为3.
(2)解:令直线与x轴的交点为E,如图所示:
将直线 与双曲线联立方程组,得:
,
解得:或,
∴点B(6,1),
将x=0代入得:y=4,
∴点D(0,4),
将y=0代入得:x=8,
∴点E(8,0),
∴S△AOB=S△DOE-S△DOA-S△BOE==8.
(3)解:将不等式 变形为,
根据函数图象可知:
当0<x<2,或者x>6时,,
∴的解集为或.
【解析】【分析】(1)先将点代入直线求得点,再将点代入即可求出的值;
(2)令直线与x轴的交点为E,根据函数解析式分别求出点D、B、E的坐标,再根据S△AOB=S△DOE-S△DOA-S△BOE即可可得结论.
(3)根据图象直接判断不等式的解集即可.
(1)将点代入 得,
,
将代入,
;
(2)令 中,得,
,
解方程组,
得或,
,
;
(3)即为,
根据图象得或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
