人教版八年级数学下册 第18章 平行四边形复习题--作图问题(含解析)
文档属性
| 名称 | 人教版八年级数学下册 第18章 平行四边形复习题--作图问题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 15:52:10 | ||
图片预览




文档简介
第18章 平行四边形复习题--作图问题
一、单选题
1.如图,在平行四边形ABCD中,,,按以下步骤作图:
①以点C为圆心,以长为半径作弧,交于点F;②分别以点D,F为圆心,以长为半径作弧,两弧相交于点G,作射线交于点E,则的长为( )
A.4 B. C. D.
2.如图,在中,,BE是AC边上的中线.按下列步骤作图:①分别以点B,C为圆心,大于线段BC长度一半的长为半径作弧,相交于点M,N;②过点M,N作直线MN,交BC于点D;③连接DE.则线段DE的长为( ).
A.5 B.4 C.3 D.2
3.已知:如图,,小静进行了以下作图:①在的两边上分别截取,,使;②分别以点,为圆心,长为半径作弧,两弧交于点;③连接,,,.若,,则的长为( )
A.5 B.4 C.3 D.2
4.在平面直角坐标系中,矩形的边在轴上,为线段的中点,矩形的顶点,,连接按照下列方法作图:以点为圆心,适当的长度为半径画弧分别交、于点、;分别以点、为圆心,大于的长为半径画弧交于点;作射线交于,则线段的长为( )
A. B.1 C. D.
5.如图,在平行四边形ABCD中,,的面积等于.根据作图痕迹,计算出平行四边形ABCD的面积为( )
A. B. C. D.
6.如图,在菱形中,按以下步骤作图,下列结论中错误的是( )
(1)分别以,为圆心,大于长为半径作弧,两弧分别交于点,;
(2)作直线,且直线恰好经过点,且与边交于点;
(3)连接.
A. B.
C. D.
7.如图,中,,平分交于点D,按下列步骤作图.
步骤1:分别以点C和点D为圆心,以大于的长为半径画弧,两弧相交于M,N两点;
步骤2:作直线,分别交,于点E,F;
步骤3:连接,.
若,,则线段的长为( )
A. B. C. D.
8.如图,在中,按以下步骤作图:①分别以点,为圆心,大于的长为半径画弧,两弧相交于,两点,和交于点;②以点为圆心,长为半径画弧,交于点;③分别以点,为圆心,大于的长为半径画弧,两弧相交于点,连接,和相交于点,连接.若,,则的长为( )
A.2.5 B.3 C.3.5 D.4
9.如图,平行四边形ABCD中,,,按以下步骤作图:①以点为圆心,适当长为半径画弧,分别交于点,交于点;②分别以点,为圆心,大于的长为半径画弧,两弧在内相交于点;③画射线,交于点,交对角线于点.若,则的长度为( )
A.3 B. C. D.
10.如图,在矩形中,按以下步骤作图:①以点B为圆心,适当长为半径画弧,分别交,于点N,M;②分别以M,N为圆心,大于的长为半径画弧,两弧在矩形内交于点G;③作射线,若,F为边的中点,E为射线上一动点,则的最小值为( )
A.3 B. C. D.5
11.如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,AB长为半径画弧,交边AD于点;②再分别以B,F为圆心画弧,两弧交于平行四边形ABCD内部的点G处;③连接AG并延长交BC于点E,连接BF,若BF=3,AB=2.5,则AE的长为( )
A.2 B.4 C.8 D.5
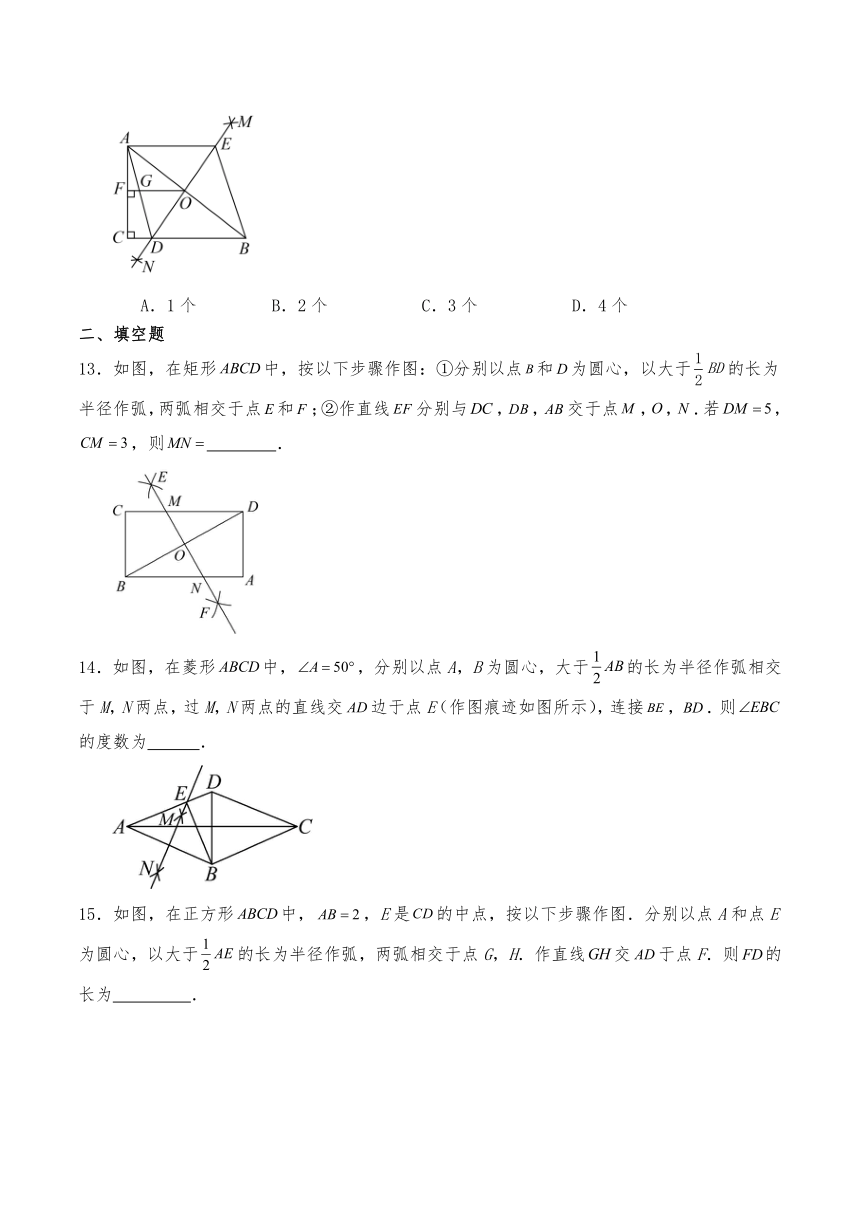
12.如图,在中,,,按以下步骤作图:(1)分别以点为圆心,以大于的长为半径作弧,两弧相交于两点(点M在的上方);(2)作直线交于点O,交于点D;(3)用圆规在射线上截取.连接,过点O作,垂足为F,交于点G.下列结论:
①;②;③;④若,则四边形的周长为25.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
13.如图,在矩形中,按以下步骤作图:①分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;②作直线分别与,,交于点,,.若,,则 .
14.如图,在菱形中,,分别以点A,B为圆心,大于的长为半径作弧相交于M,N两点,过M,N两点的直线交边于点E(作图痕迹如图所示),连接,.则的度数为 .
15.如图,在正方形中,,E是的中点,按以下步骤作图.分别以点A和点E为圆心,以大于的长为半径作弧,两弧相交于点G,H.作直线交于点F.则的长为 .
16.如图,的顶点,按下步骤作图:①以点O为圆心,适当长为半径作弧,分别交OA、OB于点D、E;②分别以点D、E为圆心,大于DE的一半长为半径作弧,两弧交于点F;③作射线OF,交边AC于点G.则AG的长度为 .
17.如图,在平行四边形中,按如下步骤作图:①以点为圆心,以适当长为半径画弧,分别交,于点,;②分别以点,为圆心,以大于的长为半径画弧,两弧在内交于点;③作射线交于点.若,则为 .
18.如图,矩形中,,连接,按下列方法作图:以点C为圆心,适当长为半径画弧,分别交、于点E、F;分别以点E、F为圆心,大于的长为半径画弧,两弧交于点G;作射线交于点H,则的长度为 .
19.如图,在菱形中,,按以下步骤作图:分别以点和点为圆心,大于的长为半径画弧,两弧交于点,;作直线,且恰好经过点,与交于点,连接,则的值为 .
20.(1)如图,点,分别是锐角两边上的点,,分别以点,为圆心,以的长为半径画弧,两弧相交于点,连接,.则根据作图过程判定四边形是菱形的依据是 .
(2)如图,在菱形中,,为的中点,将沿翻折得到,射线交于点,若,则 .
21.如图,在平行四边形ABCD中,按以下步骤作图:①以点A为圆心,的长为半径画弧,交于点F;②分别以点F,B为圆心,以大于的长为半径画弧,两弧在内交于点G;③作射线,交边于点E,交于点O,连接.若,,则四边形的面积为 .
22.如图,在△ABC中,∠ACB=90°.按以下步骤作图,分别以点A和点B为圆心,大于的长为半径作圆弧,两弧交于点E和点F;作直线EF交AB于点D;连结CD,若AC=8,BC=6,则CD的长为 .
23.如图,在矩形中,分别以点B、D为圆心,大于长为半径画弧,两弧分别交于点M、N,过点M、N作直线分别交、于点E、F.若,,则的长是 .
24.如图,正方形ABCD的对角线AC与BD相交于点O,以点C为圆心,适当长为半径画弧,分别交AC,BC于点E、F,分别以点E、F为圆心,大于长为半径画弧,两弧交于点G,连接CG,并延长交DB于M点,若,则线段 .
三、解答题
25.如图,在菱形中,对角线和相交于点.
(1)实践与操作:过点作DE∥AC交的延长线于点.(要求:尺规作图,保留作图痕迹,不写作法,标明字母)
(2)猜想与证明:试猜想线段与之间的数量关系,并证明你的猜想.
26.数学活动课上,小明想取平行四边形的对角线上一点构造一个新平行四边形,具体的做法是:如图,在□的对角线上取一点,连接,,再过点作,交于点,连接,得到四边形,进一步证明四边形是平行四边形.按以上思路完成下面的作图与填空.
证明:用直尺和圆规过点作,交于点,连接.保留作图痕迹
在和中,
四边形是平行四边形,
, ① ,
② .
,
③ .
.
④ ,
四边形是平行四边形.
27.如图,在中,是 的角平分线.
(1)请用圆规和无刻度的直尺作的垂直平分线,分别交,于点,;(保留作图痕迹,不写作法)
(2)连接,,试判断四边形的形状,并证明.
28.学习过程中,小胡发现:四边形是平行四边形,平分交于点,若过点作的垂线,交于点,交于点,连接,则必有四边形为菱形.为验证此规律的正确性,小胡思路是:在下图中,过点作的垂线,再通过证明全等得出结论.请完成以下作图与填空:
(1)用直尺和圆规在下图的基础上过点作的垂线,交于点,交于点,再连接.(只保留作图痕迹)
(2)求证:四边形为菱形请补全下列过程.
证明:∵四边形是平行四边形,
∴,
∴,
∵平分,
∴ ① ,
∴ ② ,
∴.
∵,
∴
∴在和中,
∴(),
∴ ③ .
∴.
又∵,
∴ ④
又∵,
∴四边形是菱形.
29.在中,,为的角平分线.作线段的垂直平分线,分别交、于点、,垂足为.连接、.则四边形是正方形.补全图形(保留作图痕迹,不写作法)并完成以下证明.
证明:∵平分,且
∴又垂直平分,
∴,
∴,同理
∴
∴,
∵垂直平分,
∴① ,② .(③写推理依据 )
∴,
∴四边形是④ .
又∵,
∴四边形是正方形.
30.教材呈现
例:如图(1),在中,,是斜边上的中线.求证:.
证明:延长CD至点E,使,连接.
……
(1)请根据教材提示,结合图(1)写出完整的证明过程.
(2)初步探究
如图(2),在四边形中,,,,于点P,连接,,且.
①的度数为______.
②求的长.
(3)拓展运用
如图(3),在平行四边形ABCD中,,,F是边上一点,且;按以下步骤作图:①以点B为圆心,以适当的长为半径作弧,分别交,于点M,N;②分别以点M,N为圆心,以大于的长为半径作弧,两弧交于点E,作射线.过点F作交于点P,过点P作于点G,Q为射线上一动点,连接,.若,请直接写出的值.
答案:
一、单选题
1.C
【分析】由平行四边形的性质可得,由勾股定理即可求解.
解:四边形是平行四边形,
∴,
∴
由题意可得,
∴
∴.
故选:C.
2.C
【分析】根据作法得∶点D为BC的中点,然后根据三角形中位线定理,即可求解.
解:解∶根据作法得∶MN为BC的垂直平分线,即点D为BC的中点,
∵BE为AC边上的中线.即点E为AC的中点,
∴.
故选:C
3.B
【分析】根据作法判定出四边形是菱形,再根据菱形的面积等于对角线乘积的一半列式计算即可得解.
解:由作图可得,,
∴四边形是菱形,
∴,
即,
解得,
故选:B.
4.C
【分析】由作图可知,是的平分线,如图,过作于,由角平分线的性质可知,,由题意得,设,则,,在中,由勾股定理得,即,计算求解即可.
解:由作图可知,是的平分线,如图,过作于,
由角平分线的性质可知,由勾股定理得:,
∵矩形的顶点D,O为线段的中点,
∴,,
∴,
设,则,,
在中,由勾股定理得,即,
解得,
∴,
故选:C.
5.A
【分析】根据线段垂直平分线性质得到,得到,得到,根据,得到,得到,得到.
本题主要考查了线段垂直平分线,平行四边形,三角形面积.熟练掌握线段垂直平分线性质,平行四边形性质,等高三角形面积比等于底边比,是解决问题的关键.
解:由作图知,垂直平分,
∴,
∴,
∴,
∵,
∴,
∴,
∵是中心对称图形,对称中心是点O,
∴,
∴.
故选:A.
6.B
【分析】连接,,先根据菱形的性质可得,即可判断选项C正确;再证是等边三角形,根据等腰三角形的三线合一即可判断选项A正确;根据菱形的性质可得,根据即可判断选项B错误;根据和三角形的面积公式即可判断选项D正确.
解:如图,连接,,
由题意可知,垂直平分,
,
四边形是菱形,
,
,,选项C正确;
是等边三角形,
,
(等腰三角形的三线合一),选项A正确;
又四边形是菱形,
,,
的边上的高等于的边上的高,,选项B错误;
,
,选项D正确;
故选:B.
7.B
【分析】由作图可知,四边形是正方形,根据,可得,由此即可解决问题.
解:∵平分,,
∴,
由作图可知,是的垂直平分线,
∴,,
∴,
∴,
∴四边形是正方形,
∴,,
∵,
∴,
∵,,
∴,
故选:B.
8.A
【分析】本题考查作图基本作图,三角形中位线定理,线段的垂直平分线的性质等知识,利用三角形中位线定理以及线段的垂直平分线的性质求解.
解:由作图可知垂直平分线段,平分,,
,,
,
,,
,
.
故选:A.
9.A
【分析】先根据平行四边形的性质得到BC=AD=10,再利用勾股定理计算出AC=8,利用基本作图得到BQ平分∠ABC,则根据角平分线的性质得到点O到BA的距离等于点O到BC的距离,接着利用三角形的面积公式得到S△ABO:S△BCO=AB:BC=OA:OC,所以OAAC.
解:∵四边形ABCD为平行四边形,
∴BC=AD=10,
∵BA⊥CA,
∴∠BAC=90°,
在Rt△ABC中,AC8,
由作法得BQ平分∠ABC,
∴点O到BA的距离等于点O到BC的距离,
∴S△ABO:S△BCO=AB:BC=6:10=3:5,
∵S△ABO:S△BCO=OA:OC,
∴OA:OC=3:5,
∴OA:AC=3:8,
∴OAAC8=3.
故选:A.
10.B
【分析】在上截取,连接,可证(),可得,当、、三点共线时,最小,即最小,由即可求解.
解:如图,在上截取,连接,
由作法可得平分,
,
在和中
,
(),
,
,
当、、三点共线时,最小,
即最小,
四边形是矩形,
,
是的中点,
,
,
的最小值;
故选:B.
11.B
【分析】连接EF,先证AF=AB=BE,得四边形ABEF是菱形,据此知AE与BF互相垂直平分,继而得OB的长,由勾股定理求得OA的长,继而得出答案.
解:由题意得:AF=AB,AE为∠BAD的角平分线,则∠BAE=∠FAE.
又∵四边形ABCD是平行四边形,则AD∥BC,∠BAE=∠FAE=∠BEA,
∴AF=AB=BE.
连接EF,则四边形ABEF是菱形,
∴AE与BF互相垂直平分,
设AE与BF相交于点O,OB1.5.
在Rt△AOB中,OA2,
则AE=2OA=4.
故选:B.
12.D
【分析】证明四边形ADBE是菱形,推出FG是△ACD的中位线,即可得到,由此判断①;根据菱形的性质得到AD=BD,再利用Rt△ACD得到,即可判断②;根据FG是△ACD的中位线,证得,即可判断③;设OA=x,则OF=9-x,根据,求出OA=5得到AB=10,BC=8,再根据,求出BD=,即可判断④.
解:由题意知:MN垂直平分AB,
∴OA=OB,ED⊥AB,
∵OD=OE,
∴四边形ADBE是菱形,
∵,,
∴OF∥BC,AF=CF,
∴FG是△ACD的中位线,
∴,故①正确;
∵四边形ADBE是菱形,
∴AD=BD,
在Rt△ACD中,,
∴ ,故②正确;
∵FG是△ACD的中位线,
∴点G是AD的中点,
∴,
∵,
∴,故③正确;
∵AC=6,
∴AF=3,
设OA=x,则OF=9-x,
∵,
∴,
解得x=5,
∴AB=10,
∴BC=8,
∵,
∴,
解得BD=,
∴四边形的周长为.
故选:D.
13.
14.
【分析】本题考查了作图—垂直平分线,菱形的性质,根据题意得,点E在的垂直平分线上,则,即可得,根据四边形为菱形得,,可得,即可得;掌握作图—垂直平分线,菱形的性质是解题的关键.
解:根据题意得,点E在的垂直平分线上,
∴,
∴,
∵四边形为菱形,
∴,
,
∴,
∴,
故答案为:.
15.
【分析】本题考查正方形的性质,作线段垂直平分线,线段垂直平分线的性质,勾股定理,熟练掌握线段垂直平分线的作法和性质、勾股定理是解题的关键.先由作法得出且平分,从而得到,在中,设,则,由勾股定理,得,求解即可.
解:连接,
由作图可知,且平分,
,
∵正方形,
∴,,
∵E是的中点,
,
在中,设,则,
由勾股定理,得,
解得:,
∴,
故答案为:.
16.
【分析】如图,先利用勾股定理计算出OA=,再利用基本作图和平行线的性质得到∠AOG=∠AGO,则AG=AO=,从而求解.
解:如图,∵ AOBC的顶点A的坐标为,
∴ACOB,OA=,
由作法得OG平分∠AOB,
∴∠AOG=∠BOG,
而ACOB,
∴∠AGO=∠BOG,
∴∠AOG=∠AGO,
∴AG=AO=,
故答案为:.
17.
【分析】先利用基本作图得,再根据平行四边形的性质和平行线的性质得到,从而得到.
解:由作法得平分,
,
四边形为平行四边形,
,
,
,
.
故答案为:.
18.
【分析】证明,,,如图,过H点作于M,可得,证明,求解,从而可得答案.
解:∵矩形中,,
∴,,,
如图,过H点作于M,
由作法得平分,
∵,,
∴,
∴,
∴,
∵,,
∴,
∴,而,
∴.
故答案为.
19.
【分析】本题考查了作图基本作图:熟练掌握基本作图作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线.
利用基本作法得到得垂直平分,即,,再利用菱形的性质得到,,则利用勾股定理先计算出,然后计算出.
解:由作法得垂直平分,即,,
四边形为菱形,
,,
,,
在中,,
在中,.
故答案为.
20. 四条边都相等的四边形是菱形
【分析】(1)由AE=AF=ED=DF,根据四条边都相等的四边形是菱形,即可证得:四边形AEDF是菱形.
(2)DE和CB的延长线相交于G'点,连结EF,作EH⊥DF于H点,如图,根据菱形的性质得A=180°﹣∠B=120°,AB=AD=2,AD∥BC,则∠1=∠G,再利用折叠的性质得∠1=∠2,DG=DA=2,EG=EA=1,∠3=∠A=120°,则∠4=60°,在Rt△EHG中利用含30度的直角三角形三边的关系得到HG=EG=,EH=EH=,则在Rt△DEH中利用勾股定理可计算出DE=,再证明∠2=∠G'得到FG'=FD,证明△AED≌△BEG'得到DE=G'E,所以FE⊥DG',然后证明Rt△DEF∽Rt△DHE,利用相似比计算出DF=,则FG=FD﹣DG=,于是得到BF=FG=.
解:(1)根据作图过程判定四边形ABDC是菱形的依据是:四边相等的四边形是菱形,
理由如下:
∵根据题意得:AE=AF=ED=DF,
∴四边形AEDF是菱形,
(2)DE和CB的延长线相交于G'点,连结EF,作EH⊥DF于H点,如图,
∵四边形ABCD为菱形,
∴∠A=180°﹣∠B=120°,AB=AD=2,AD∥BC
∴∠1=∠G',
而E为AB的中点,
∴AE=BE=1,
∵△AED沿DE翻折得到△GED,
∴∠1=∠2,DG=DA=2,EG=EA=1,∠3=∠A=120°,
∴∠4=60°,
∴在Rt△EHG中,HG=EG=,EH=,
∴在Rt△DEH中,DE=,
∵AD∥BG',
∴∠1=∠G',
∴∠G'=∠2,
∴FG'=FD,
在△AED和△BEG'中,
,
∴△AED≌△BEG',
∴DE=G'E,AD=BG'=2,
∴FE⊥DG',
∴∠FED=90°,
∵∠HDE=∠EDF,
∴Rt△DEF∽Rt△DHE,
∴,即,
∴DF=,
∴FG=FD﹣DG=﹣2=,
∵FG'=FD,BG'=DG=2,
∴FG'-BG'=FD-DG,
∴BF=FG=.
故答案为:(1)四条边都相等的四边形是菱形,(2).
21.24.
【分析】根据作图可知AG是角平分线,根据等腰三角形的性质判断四边形AFEB是菱形,求出对角线长即可求面积.
解:由作图可知,AG平分∠BAF,AB=AF,
∴AG垂直平分BF,∠FAG=∠BAE,
∴EF=EB,
∵AD∥BE,
∴∠FAE=∠AEB,
∴∠BAE =∠AEB,
∴AB=BE,
∴AB=BE=EF=AF,
∴四边形ABEF是菱形,
∴BO=FO=4,
∴,
AE=6,
菱形的面积为;
故答案为:24.
22.5
【分析】先根据勾股定理求出AB的长,再由作图的方法得出EF是线段AB的垂直平分线,故可得出点D是线段AB的中点,由直角三角形的性质即可得出结论.
解:∵在△ABC中,∠ACB=90°,AC=8,BC=6,
∴AB===10.
∵由题意可知,EF是线段AB的垂直平分线,
∴点D是线段AB的中点,
∴CD=AB=5.
故答案为5.
23.
【分析】设与交于点G,连接,首先根据作图过程可知:是的垂直平分线,,,可得,再根据矩形的性质及勾股定理可求得,设,则,利用勾股定理即可求得、的长,再根据全等三角形的判定,可证得,可得,据此即可求解.
解:如图:设与交于点G,连接,
根据作图过程可知:是的垂直平分线,
,,
,
四边形是矩形,
,,,
在中,,
设,则,
在中,,
得,
解得,
,,
,
,
在与中,
,
,
,
,
故答案为:.
24.1
【分析】过点N作于点H,由四边形ABCD是正方形,得到是等腰直角三角形,继而求出,再根据角平分线的性质定理得出,再由外角的性质得到,最后由等角对等边得出BM的长度即可.
解:
如图,过点N作于点H
四边形ABCD是正方形
是等腰直角三角形
由作图可知,CM平分
,
故答案为:1
三、解答题
25.
解:(1)如下如:即为所求,
以点为圆心,为半径,画弧交的延长线于点,连接,
证明:
∵四边形是菱形,
∴,,
∴,
∵,
∴,
∴四边形是平行四边形,
∴.
(2)∵四边形是菱形,
∴,
∵,
∴,
∴是上的中线,
∴.
26.
解:如图所示,
在和中,
四边形是平行四边形,
,,
.
,
.
.
,
四边形是平行四边形.
故答案为:;;;.
27.
解:(1)图形如图所示:
(2)结论:四边形是菱形.
理由:设交于点.
垂直平分线段,
,,
平分,
,
,,
,
,
四边形是菱形.
28.
(1)解:如图所示,
(2)证明:∵四边形是平行四边形,
∴,
∴,
∵平分,
∴,
∴,
∴.
∵,
∴
∴在和中,
∴(),
∴.
∴.
又∵,
∴四边形为平行四边形.
又∵,
∴四边形是菱形.
故答案为:①;②;③;④四边形为平行四边形.
29.
解:作图如图所示,
证明:∵平分,且,
∴,
又∵垂直平分,
∴,
∴,
同理
∴,
∴,
∵垂直平分,
∴,,(线段垂直平分线上的点到线段两端的距离相等)
∴,
∴四边形是菱形,
又∵,
∴四边形是正方形.
故答案为:①;②;③线段垂直平分线上的点到线段两端的距离相等;④菱形.
30.
解:(1)证明:延长至点E,使,连接,,
则.
∵是斜边上的中线,
∴,
∴四边形是平行四边形.
∵,
∴四边形是矩形,
∴,
∴.
(2)①∵,,,
∴P为中点,
∴,
∴,,
∵,
∴,
∴,
故答案为:
②如图(1),过点D作于点G.
由题意,,
∴,
∴,
∴,.
由①知,
∴.
设,则,.
∵,
∴,
解得,
∴.
(3)或3.
解:过点Q作于点H.
∵,
∴.
由作图可知,平分,
∴,
∴,
∴;
分两种情况:①如图(2),当点Q在线段上时,连接,
则,
∴由勾股定理得:;
∵,,
∴.
在中,,
∴,,
∴.
在中,,
②如图(3),当点Q在线段BP的延长线上时,
由题意,,.
在中,,
∴,,
∴.
在中,
,
综上可知,的值为或3.
一、单选题
1.如图,在平行四边形ABCD中,,,按以下步骤作图:
①以点C为圆心,以长为半径作弧,交于点F;②分别以点D,F为圆心,以长为半径作弧,两弧相交于点G,作射线交于点E,则的长为( )
A.4 B. C. D.
2.如图,在中,,BE是AC边上的中线.按下列步骤作图:①分别以点B,C为圆心,大于线段BC长度一半的长为半径作弧,相交于点M,N;②过点M,N作直线MN,交BC于点D;③连接DE.则线段DE的长为( ).
A.5 B.4 C.3 D.2
3.已知:如图,,小静进行了以下作图:①在的两边上分别截取,,使;②分别以点,为圆心,长为半径作弧,两弧交于点;③连接,,,.若,,则的长为( )
A.5 B.4 C.3 D.2
4.在平面直角坐标系中,矩形的边在轴上,为线段的中点,矩形的顶点,,连接按照下列方法作图:以点为圆心,适当的长度为半径画弧分别交、于点、;分别以点、为圆心,大于的长为半径画弧交于点;作射线交于,则线段的长为( )
A. B.1 C. D.
5.如图,在平行四边形ABCD中,,的面积等于.根据作图痕迹,计算出平行四边形ABCD的面积为( )
A. B. C. D.
6.如图,在菱形中,按以下步骤作图,下列结论中错误的是( )
(1)分别以,为圆心,大于长为半径作弧,两弧分别交于点,;
(2)作直线,且直线恰好经过点,且与边交于点;
(3)连接.
A. B.
C. D.
7.如图,中,,平分交于点D,按下列步骤作图.
步骤1:分别以点C和点D为圆心,以大于的长为半径画弧,两弧相交于M,N两点;
步骤2:作直线,分别交,于点E,F;
步骤3:连接,.
若,,则线段的长为( )
A. B. C. D.
8.如图,在中,按以下步骤作图:①分别以点,为圆心,大于的长为半径画弧,两弧相交于,两点,和交于点;②以点为圆心,长为半径画弧,交于点;③分别以点,为圆心,大于的长为半径画弧,两弧相交于点,连接,和相交于点,连接.若,,则的长为( )
A.2.5 B.3 C.3.5 D.4
9.如图,平行四边形ABCD中,,,按以下步骤作图:①以点为圆心,适当长为半径画弧,分别交于点,交于点;②分别以点,为圆心,大于的长为半径画弧,两弧在内相交于点;③画射线,交于点,交对角线于点.若,则的长度为( )
A.3 B. C. D.
10.如图,在矩形中,按以下步骤作图:①以点B为圆心,适当长为半径画弧,分别交,于点N,M;②分别以M,N为圆心,大于的长为半径画弧,两弧在矩形内交于点G;③作射线,若,F为边的中点,E为射线上一动点,则的最小值为( )
A.3 B. C. D.5
11.如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,AB长为半径画弧,交边AD于点;②再分别以B,F为圆心画弧,两弧交于平行四边形ABCD内部的点G处;③连接AG并延长交BC于点E,连接BF,若BF=3,AB=2.5,则AE的长为( )
A.2 B.4 C.8 D.5
12.如图,在中,,,按以下步骤作图:(1)分别以点为圆心,以大于的长为半径作弧,两弧相交于两点(点M在的上方);(2)作直线交于点O,交于点D;(3)用圆规在射线上截取.连接,过点O作,垂足为F,交于点G.下列结论:
①;②;③;④若,则四边形的周长为25.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
13.如图,在矩形中,按以下步骤作图:①分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;②作直线分别与,,交于点,,.若,,则 .
14.如图,在菱形中,,分别以点A,B为圆心,大于的长为半径作弧相交于M,N两点,过M,N两点的直线交边于点E(作图痕迹如图所示),连接,.则的度数为 .
15.如图,在正方形中,,E是的中点,按以下步骤作图.分别以点A和点E为圆心,以大于的长为半径作弧,两弧相交于点G,H.作直线交于点F.则的长为 .
16.如图,的顶点,按下步骤作图:①以点O为圆心,适当长为半径作弧,分别交OA、OB于点D、E;②分别以点D、E为圆心,大于DE的一半长为半径作弧,两弧交于点F;③作射线OF,交边AC于点G.则AG的长度为 .
17.如图,在平行四边形中,按如下步骤作图:①以点为圆心,以适当长为半径画弧,分别交,于点,;②分别以点,为圆心,以大于的长为半径画弧,两弧在内交于点;③作射线交于点.若,则为 .
18.如图,矩形中,,连接,按下列方法作图:以点C为圆心,适当长为半径画弧,分别交、于点E、F;分别以点E、F为圆心,大于的长为半径画弧,两弧交于点G;作射线交于点H,则的长度为 .
19.如图,在菱形中,,按以下步骤作图:分别以点和点为圆心,大于的长为半径画弧,两弧交于点,;作直线,且恰好经过点,与交于点,连接,则的值为 .
20.(1)如图,点,分别是锐角两边上的点,,分别以点,为圆心,以的长为半径画弧,两弧相交于点,连接,.则根据作图过程判定四边形是菱形的依据是 .
(2)如图,在菱形中,,为的中点,将沿翻折得到,射线交于点,若,则 .
21.如图,在平行四边形ABCD中,按以下步骤作图:①以点A为圆心,的长为半径画弧,交于点F;②分别以点F,B为圆心,以大于的长为半径画弧,两弧在内交于点G;③作射线,交边于点E,交于点O,连接.若,,则四边形的面积为 .
22.如图,在△ABC中,∠ACB=90°.按以下步骤作图,分别以点A和点B为圆心,大于的长为半径作圆弧,两弧交于点E和点F;作直线EF交AB于点D;连结CD,若AC=8,BC=6,则CD的长为 .
23.如图,在矩形中,分别以点B、D为圆心,大于长为半径画弧,两弧分别交于点M、N,过点M、N作直线分别交、于点E、F.若,,则的长是 .
24.如图,正方形ABCD的对角线AC与BD相交于点O,以点C为圆心,适当长为半径画弧,分别交AC,BC于点E、F,分别以点E、F为圆心,大于长为半径画弧,两弧交于点G,连接CG,并延长交DB于M点,若,则线段 .
三、解答题
25.如图,在菱形中,对角线和相交于点.
(1)实践与操作:过点作DE∥AC交的延长线于点.(要求:尺规作图,保留作图痕迹,不写作法,标明字母)
(2)猜想与证明:试猜想线段与之间的数量关系,并证明你的猜想.
26.数学活动课上,小明想取平行四边形的对角线上一点构造一个新平行四边形,具体的做法是:如图,在□的对角线上取一点,连接,,再过点作,交于点,连接,得到四边形,进一步证明四边形是平行四边形.按以上思路完成下面的作图与填空.
证明:用直尺和圆规过点作,交于点,连接.保留作图痕迹
在和中,
四边形是平行四边形,
, ① ,
② .
,
③ .
.
④ ,
四边形是平行四边形.
27.如图,在中,是 的角平分线.
(1)请用圆规和无刻度的直尺作的垂直平分线,分别交,于点,;(保留作图痕迹,不写作法)
(2)连接,,试判断四边形的形状,并证明.
28.学习过程中,小胡发现:四边形是平行四边形,平分交于点,若过点作的垂线,交于点,交于点,连接,则必有四边形为菱形.为验证此规律的正确性,小胡思路是:在下图中,过点作的垂线,再通过证明全等得出结论.请完成以下作图与填空:
(1)用直尺和圆规在下图的基础上过点作的垂线,交于点,交于点,再连接.(只保留作图痕迹)
(2)求证:四边形为菱形请补全下列过程.
证明:∵四边形是平行四边形,
∴,
∴,
∵平分,
∴ ① ,
∴ ② ,
∴.
∵,
∴
∴在和中,
∴(),
∴ ③ .
∴.
又∵,
∴ ④
又∵,
∴四边形是菱形.
29.在中,,为的角平分线.作线段的垂直平分线,分别交、于点、,垂足为.连接、.则四边形是正方形.补全图形(保留作图痕迹,不写作法)并完成以下证明.
证明:∵平分,且
∴又垂直平分,
∴,
∴,同理
∴
∴,
∵垂直平分,
∴① ,② .(③写推理依据 )
∴,
∴四边形是④ .
又∵,
∴四边形是正方形.
30.教材呈现
例:如图(1),在中,,是斜边上的中线.求证:.
证明:延长CD至点E,使,连接.
……
(1)请根据教材提示,结合图(1)写出完整的证明过程.
(2)初步探究
如图(2),在四边形中,,,,于点P,连接,,且.
①的度数为______.
②求的长.
(3)拓展运用
如图(3),在平行四边形ABCD中,,,F是边上一点,且;按以下步骤作图:①以点B为圆心,以适当的长为半径作弧,分别交,于点M,N;②分别以点M,N为圆心,以大于的长为半径作弧,两弧交于点E,作射线.过点F作交于点P,过点P作于点G,Q为射线上一动点,连接,.若,请直接写出的值.
答案:
一、单选题
1.C
【分析】由平行四边形的性质可得,由勾股定理即可求解.
解:四边形是平行四边形,
∴,
∴
由题意可得,
∴
∴.
故选:C.
2.C
【分析】根据作法得∶点D为BC的中点,然后根据三角形中位线定理,即可求解.
解:解∶根据作法得∶MN为BC的垂直平分线,即点D为BC的中点,
∵BE为AC边上的中线.即点E为AC的中点,
∴.
故选:C
3.B
【分析】根据作法判定出四边形是菱形,再根据菱形的面积等于对角线乘积的一半列式计算即可得解.
解:由作图可得,,
∴四边形是菱形,
∴,
即,
解得,
故选:B.
4.C
【分析】由作图可知,是的平分线,如图,过作于,由角平分线的性质可知,,由题意得,设,则,,在中,由勾股定理得,即,计算求解即可.
解:由作图可知,是的平分线,如图,过作于,
由角平分线的性质可知,由勾股定理得:,
∵矩形的顶点D,O为线段的中点,
∴,,
∴,
设,则,,
在中,由勾股定理得,即,
解得,
∴,
故选:C.
5.A
【分析】根据线段垂直平分线性质得到,得到,得到,根据,得到,得到,得到.
本题主要考查了线段垂直平分线,平行四边形,三角形面积.熟练掌握线段垂直平分线性质,平行四边形性质,等高三角形面积比等于底边比,是解决问题的关键.
解:由作图知,垂直平分,
∴,
∴,
∴,
∵,
∴,
∴,
∵是中心对称图形,对称中心是点O,
∴,
∴.
故选:A.
6.B
【分析】连接,,先根据菱形的性质可得,即可判断选项C正确;再证是等边三角形,根据等腰三角形的三线合一即可判断选项A正确;根据菱形的性质可得,根据即可判断选项B错误;根据和三角形的面积公式即可判断选项D正确.
解:如图,连接,,
由题意可知,垂直平分,
,
四边形是菱形,
,
,,选项C正确;
是等边三角形,
,
(等腰三角形的三线合一),选项A正确;
又四边形是菱形,
,,
的边上的高等于的边上的高,,选项B错误;
,
,选项D正确;
故选:B.
7.B
【分析】由作图可知,四边形是正方形,根据,可得,由此即可解决问题.
解:∵平分,,
∴,
由作图可知,是的垂直平分线,
∴,,
∴,
∴,
∴四边形是正方形,
∴,,
∵,
∴,
∵,,
∴,
故选:B.
8.A
【分析】本题考查作图基本作图,三角形中位线定理,线段的垂直平分线的性质等知识,利用三角形中位线定理以及线段的垂直平分线的性质求解.
解:由作图可知垂直平分线段,平分,,
,,
,
,,
,
.
故选:A.
9.A
【分析】先根据平行四边形的性质得到BC=AD=10,再利用勾股定理计算出AC=8,利用基本作图得到BQ平分∠ABC,则根据角平分线的性质得到点O到BA的距离等于点O到BC的距离,接着利用三角形的面积公式得到S△ABO:S△BCO=AB:BC=OA:OC,所以OAAC.
解:∵四边形ABCD为平行四边形,
∴BC=AD=10,
∵BA⊥CA,
∴∠BAC=90°,
在Rt△ABC中,AC8,
由作法得BQ平分∠ABC,
∴点O到BA的距离等于点O到BC的距离,
∴S△ABO:S△BCO=AB:BC=6:10=3:5,
∵S△ABO:S△BCO=OA:OC,
∴OA:OC=3:5,
∴OA:AC=3:8,
∴OAAC8=3.
故选:A.
10.B
【分析】在上截取,连接,可证(),可得,当、、三点共线时,最小,即最小,由即可求解.
解:如图,在上截取,连接,
由作法可得平分,
,
在和中
,
(),
,
,
当、、三点共线时,最小,
即最小,
四边形是矩形,
,
是的中点,
,
,
的最小值;
故选:B.
11.B
【分析】连接EF,先证AF=AB=BE,得四边形ABEF是菱形,据此知AE与BF互相垂直平分,继而得OB的长,由勾股定理求得OA的长,继而得出答案.
解:由题意得:AF=AB,AE为∠BAD的角平分线,则∠BAE=∠FAE.
又∵四边形ABCD是平行四边形,则AD∥BC,∠BAE=∠FAE=∠BEA,
∴AF=AB=BE.
连接EF,则四边形ABEF是菱形,
∴AE与BF互相垂直平分,
设AE与BF相交于点O,OB1.5.
在Rt△AOB中,OA2,
则AE=2OA=4.
故选:B.
12.D
【分析】证明四边形ADBE是菱形,推出FG是△ACD的中位线,即可得到,由此判断①;根据菱形的性质得到AD=BD,再利用Rt△ACD得到,即可判断②;根据FG是△ACD的中位线,证得,即可判断③;设OA=x,则OF=9-x,根据,求出OA=5得到AB=10,BC=8,再根据,求出BD=,即可判断④.
解:由题意知:MN垂直平分AB,
∴OA=OB,ED⊥AB,
∵OD=OE,
∴四边形ADBE是菱形,
∵,,
∴OF∥BC,AF=CF,
∴FG是△ACD的中位线,
∴,故①正确;
∵四边形ADBE是菱形,
∴AD=BD,
在Rt△ACD中,,
∴ ,故②正确;
∵FG是△ACD的中位线,
∴点G是AD的中点,
∴,
∵,
∴,故③正确;
∵AC=6,
∴AF=3,
设OA=x,则OF=9-x,
∵,
∴,
解得x=5,
∴AB=10,
∴BC=8,
∵,
∴,
解得BD=,
∴四边形的周长为.
故选:D.
13.
14.
【分析】本题考查了作图—垂直平分线,菱形的性质,根据题意得,点E在的垂直平分线上,则,即可得,根据四边形为菱形得,,可得,即可得;掌握作图—垂直平分线,菱形的性质是解题的关键.
解:根据题意得,点E在的垂直平分线上,
∴,
∴,
∵四边形为菱形,
∴,
,
∴,
∴,
故答案为:.
15.
【分析】本题考查正方形的性质,作线段垂直平分线,线段垂直平分线的性质,勾股定理,熟练掌握线段垂直平分线的作法和性质、勾股定理是解题的关键.先由作法得出且平分,从而得到,在中,设,则,由勾股定理,得,求解即可.
解:连接,
由作图可知,且平分,
,
∵正方形,
∴,,
∵E是的中点,
,
在中,设,则,
由勾股定理,得,
解得:,
∴,
故答案为:.
16.
【分析】如图,先利用勾股定理计算出OA=,再利用基本作图和平行线的性质得到∠AOG=∠AGO,则AG=AO=,从而求解.
解:如图,∵ AOBC的顶点A的坐标为,
∴ACOB,OA=,
由作法得OG平分∠AOB,
∴∠AOG=∠BOG,
而ACOB,
∴∠AGO=∠BOG,
∴∠AOG=∠AGO,
∴AG=AO=,
故答案为:.
17.
【分析】先利用基本作图得,再根据平行四边形的性质和平行线的性质得到,从而得到.
解:由作法得平分,
,
四边形为平行四边形,
,
,
,
.
故答案为:.
18.
【分析】证明,,,如图,过H点作于M,可得,证明,求解,从而可得答案.
解:∵矩形中,,
∴,,,
如图,过H点作于M,
由作法得平分,
∵,,
∴,
∴,
∴,
∵,,
∴,
∴,而,
∴.
故答案为.
19.
【分析】本题考查了作图基本作图:熟练掌握基本作图作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线.
利用基本作法得到得垂直平分,即,,再利用菱形的性质得到,,则利用勾股定理先计算出,然后计算出.
解:由作法得垂直平分,即,,
四边形为菱形,
,,
,,
在中,,
在中,.
故答案为.
20. 四条边都相等的四边形是菱形
【分析】(1)由AE=AF=ED=DF,根据四条边都相等的四边形是菱形,即可证得:四边形AEDF是菱形.
(2)DE和CB的延长线相交于G'点,连结EF,作EH⊥DF于H点,如图,根据菱形的性质得A=180°﹣∠B=120°,AB=AD=2,AD∥BC,则∠1=∠G,再利用折叠的性质得∠1=∠2,DG=DA=2,EG=EA=1,∠3=∠A=120°,则∠4=60°,在Rt△EHG中利用含30度的直角三角形三边的关系得到HG=EG=,EH=EH=,则在Rt△DEH中利用勾股定理可计算出DE=,再证明∠2=∠G'得到FG'=FD,证明△AED≌△BEG'得到DE=G'E,所以FE⊥DG',然后证明Rt△DEF∽Rt△DHE,利用相似比计算出DF=,则FG=FD﹣DG=,于是得到BF=FG=.
解:(1)根据作图过程判定四边形ABDC是菱形的依据是:四边相等的四边形是菱形,
理由如下:
∵根据题意得:AE=AF=ED=DF,
∴四边形AEDF是菱形,
(2)DE和CB的延长线相交于G'点,连结EF,作EH⊥DF于H点,如图,
∵四边形ABCD为菱形,
∴∠A=180°﹣∠B=120°,AB=AD=2,AD∥BC
∴∠1=∠G',
而E为AB的中点,
∴AE=BE=1,
∵△AED沿DE翻折得到△GED,
∴∠1=∠2,DG=DA=2,EG=EA=1,∠3=∠A=120°,
∴∠4=60°,
∴在Rt△EHG中,HG=EG=,EH=,
∴在Rt△DEH中,DE=,
∵AD∥BG',
∴∠1=∠G',
∴∠G'=∠2,
∴FG'=FD,
在△AED和△BEG'中,
,
∴△AED≌△BEG',
∴DE=G'E,AD=BG'=2,
∴FE⊥DG',
∴∠FED=90°,
∵∠HDE=∠EDF,
∴Rt△DEF∽Rt△DHE,
∴,即,
∴DF=,
∴FG=FD﹣DG=﹣2=,
∵FG'=FD,BG'=DG=2,
∴FG'-BG'=FD-DG,
∴BF=FG=.
故答案为:(1)四条边都相等的四边形是菱形,(2).
21.24.
【分析】根据作图可知AG是角平分线,根据等腰三角形的性质判断四边形AFEB是菱形,求出对角线长即可求面积.
解:由作图可知,AG平分∠BAF,AB=AF,
∴AG垂直平分BF,∠FAG=∠BAE,
∴EF=EB,
∵AD∥BE,
∴∠FAE=∠AEB,
∴∠BAE =∠AEB,
∴AB=BE,
∴AB=BE=EF=AF,
∴四边形ABEF是菱形,
∴BO=FO=4,
∴,
AE=6,
菱形的面积为;
故答案为:24.
22.5
【分析】先根据勾股定理求出AB的长,再由作图的方法得出EF是线段AB的垂直平分线,故可得出点D是线段AB的中点,由直角三角形的性质即可得出结论.
解:∵在△ABC中,∠ACB=90°,AC=8,BC=6,
∴AB===10.
∵由题意可知,EF是线段AB的垂直平分线,
∴点D是线段AB的中点,
∴CD=AB=5.
故答案为5.
23.
【分析】设与交于点G,连接,首先根据作图过程可知:是的垂直平分线,,,可得,再根据矩形的性质及勾股定理可求得,设,则,利用勾股定理即可求得、的长,再根据全等三角形的判定,可证得,可得,据此即可求解.
解:如图:设与交于点G,连接,
根据作图过程可知:是的垂直平分线,
,,
,
四边形是矩形,
,,,
在中,,
设,则,
在中,,
得,
解得,
,,
,
,
在与中,
,
,
,
,
故答案为:.
24.1
【分析】过点N作于点H,由四边形ABCD是正方形,得到是等腰直角三角形,继而求出,再根据角平分线的性质定理得出,再由外角的性质得到,最后由等角对等边得出BM的长度即可.
解:
如图,过点N作于点H
四边形ABCD是正方形
是等腰直角三角形
由作图可知,CM平分
,
故答案为:1
三、解答题
25.
解:(1)如下如:即为所求,
以点为圆心,为半径,画弧交的延长线于点,连接,
证明:
∵四边形是菱形,
∴,,
∴,
∵,
∴,
∴四边形是平行四边形,
∴.
(2)∵四边形是菱形,
∴,
∵,
∴,
∴是上的中线,
∴.
26.
解:如图所示,
在和中,
四边形是平行四边形,
,,
.
,
.
.
,
四边形是平行四边形.
故答案为:;;;.
27.
解:(1)图形如图所示:
(2)结论:四边形是菱形.
理由:设交于点.
垂直平分线段,
,,
平分,
,
,,
,
,
四边形是菱形.
28.
(1)解:如图所示,
(2)证明:∵四边形是平行四边形,
∴,
∴,
∵平分,
∴,
∴,
∴.
∵,
∴
∴在和中,
∴(),
∴.
∴.
又∵,
∴四边形为平行四边形.
又∵,
∴四边形是菱形.
故答案为:①;②;③;④四边形为平行四边形.
29.
解:作图如图所示,
证明:∵平分,且,
∴,
又∵垂直平分,
∴,
∴,
同理
∴,
∴,
∵垂直平分,
∴,,(线段垂直平分线上的点到线段两端的距离相等)
∴,
∴四边形是菱形,
又∵,
∴四边形是正方形.
故答案为:①;②;③线段垂直平分线上的点到线段两端的距离相等;④菱形.
30.
解:(1)证明:延长至点E,使,连接,,
则.
∵是斜边上的中线,
∴,
∴四边形是平行四边形.
∵,
∴四边形是矩形,
∴,
∴.
(2)①∵,,,
∴P为中点,
∴,
∴,,
∵,
∴,
∴,
故答案为:
②如图(1),过点D作于点G.
由题意,,
∴,
∴,
∴,.
由①知,
∴.
设,则,.
∵,
∴,
解得,
∴.
(3)或3.
解:过点Q作于点H.
∵,
∴.
由作图可知,平分,
∴,
∴,
∴;
分两种情况:①如图(2),当点Q在线段上时,连接,
则,
∴由勾股定理得:;
∵,,
∴.
在中,,
∴,,
∴.
在中,,
②如图(3),当点Q在线段BP的延长线上时,
由题意,,.
在中,,
∴,,
∴.
在中,
,
综上可知,的值为或3.
