沪教版七年级数学下册 17.2三角形的内角和(含解析)
文档属性
| 名称 | 沪教版七年级数学下册 17.2三角形的内角和(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 824.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 15:57:09 | ||
图片预览

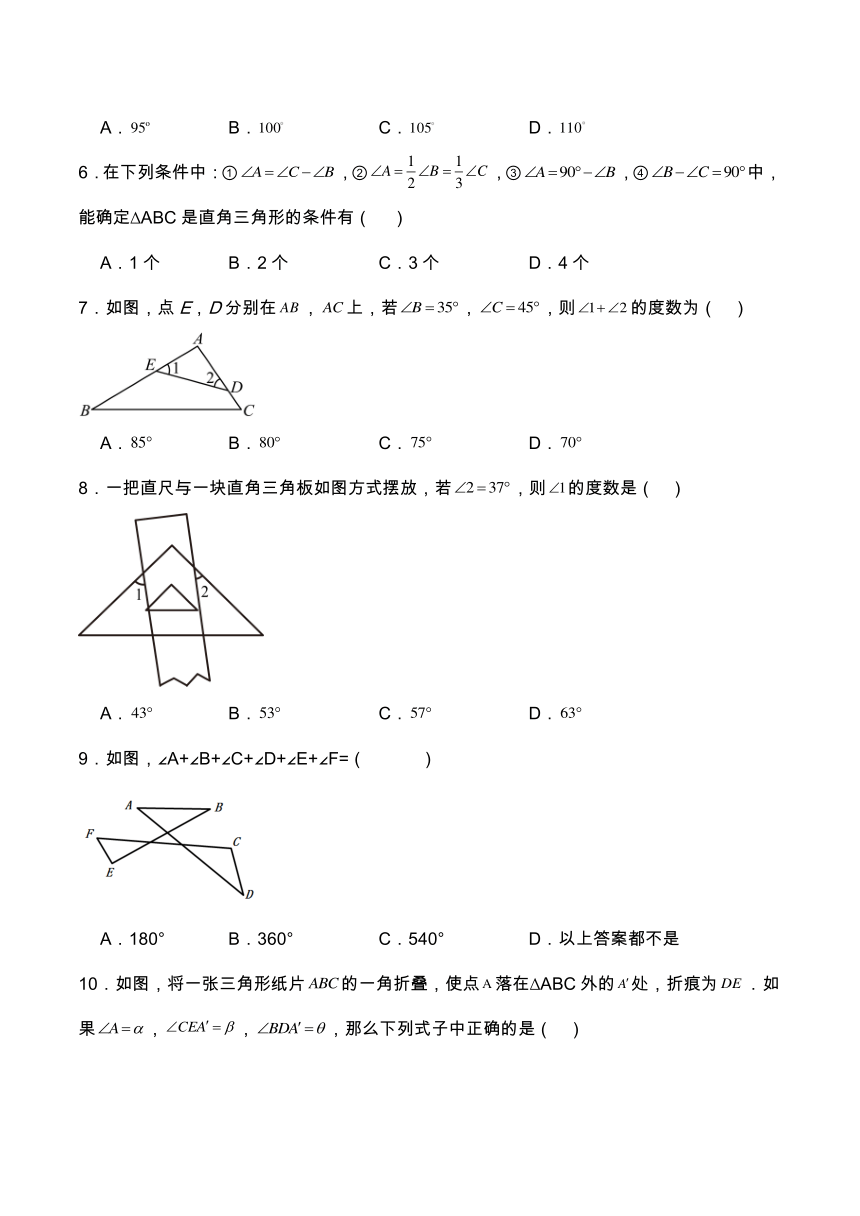

文档简介
17.2三角形的内角和
一、单选题
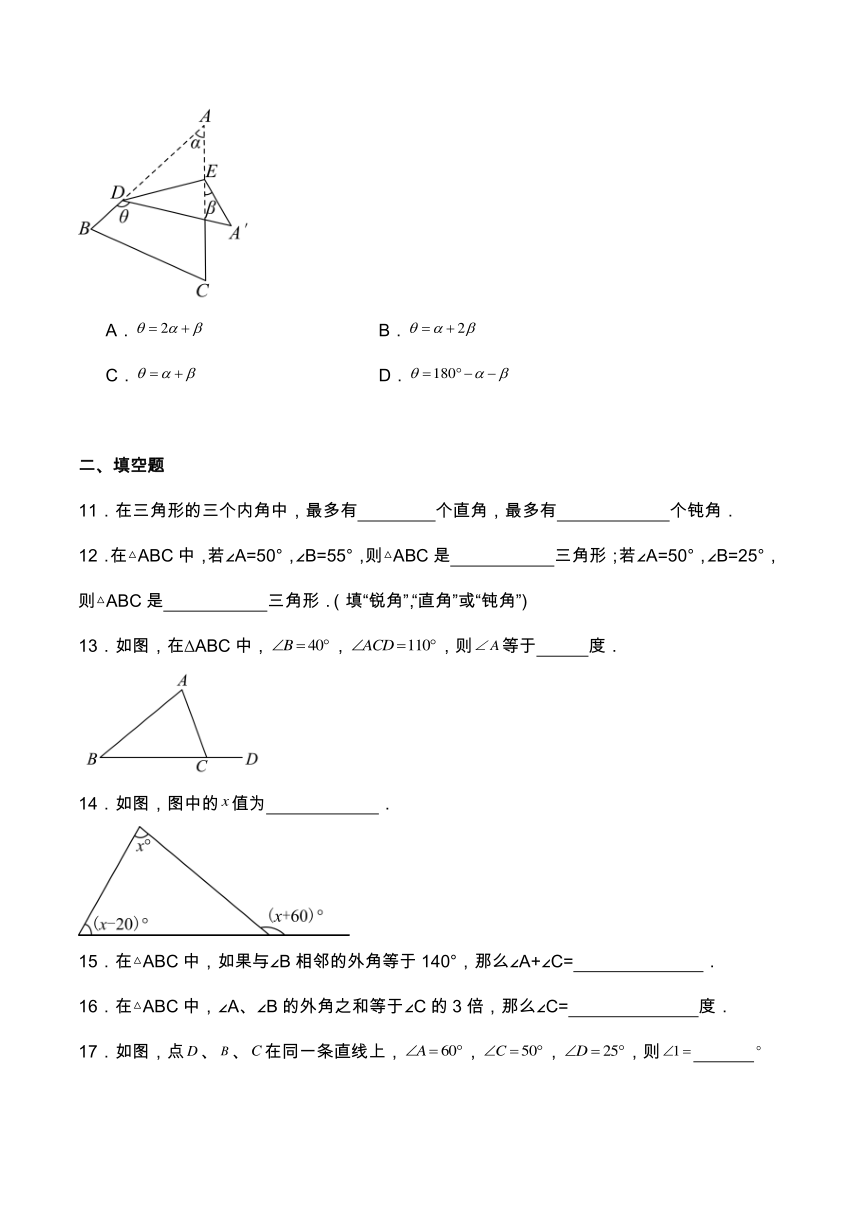
1.在 ABC中,若,,则( )
A. B. C. D.
2.如图,与的大小关系是( )
A. B. C. D.不能确定
3.如图,若,则的度数为( )
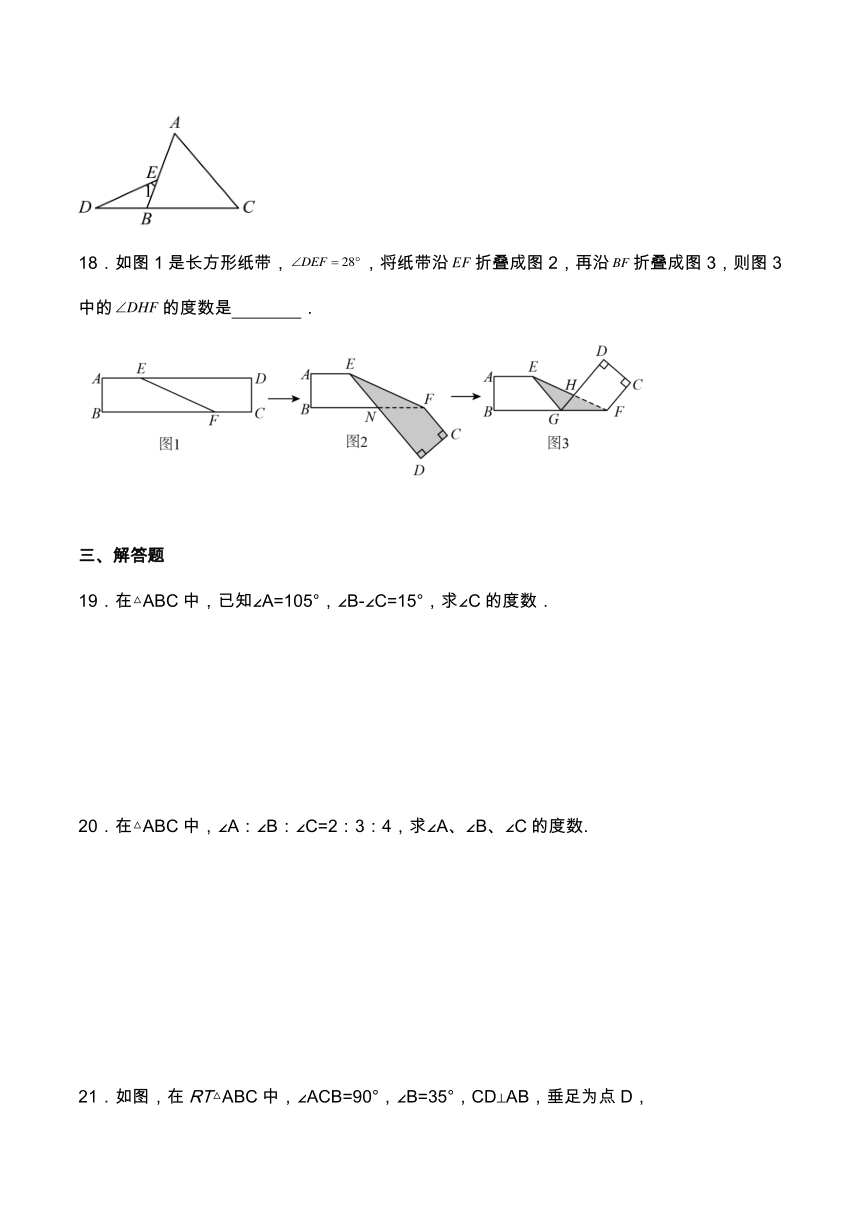
A. B. C. D.
4.如果三角形的一个外角小于与它相邻的内角,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
5.如图,点在 ABC的边上,,,则的度数为( )
A. B. C. D.
6.在下列条件中:①,②,③,④中,能确定 ABC是直角三角形的条件有( )
A.1个 B.2个 C.3个 D.4个
7.如图,点E,D分别在,上,若,,则的度数为( )
A. B. C. D.
8.一把直尺与一块直角三角板如图方式摆放,若,则的度数是( )
A. B. C. D.
9.如图,∠A+∠B+∠C+∠D+∠E+∠F=( )
A.180° B.360° C.540° D.以上答案都不是
10.如图,将一张三角形纸片的一角折叠,使点落在 ABC外的处,折痕为.如果,,,那么下列式子中正确的是( )
A. B.
C. D.
二、填空题
11.在三角形的三个内角中,最多有 个直角,最多有 个钝角.
12.在△ABC中,若∠A=50°,∠B=55°,则△ABC是 三角形;若∠A=50°,∠B=25°,则△ABC是 三角形.(填“锐角”,“直角”或“钝角”)
13.如图,在 ABC中,,,则等于 度.
14.如图,图中的值为 .
15.在△ABC中,如果与∠B相邻的外角等于140°,那么∠A+∠C= .
16.在△ABC中,∠A、∠B的外角之和等于∠C的3倍,那么∠C= 度.
17.如图,点、、在同一条直线上,,,,则
18.如图1是长方形纸带,,将纸带沿折叠成图2,再沿折叠成图3,则图3中的的度数是 .
三、解答题
19.在△ABC中,已知∠A=105°,∠B-∠C=15°,求∠C的度数.
20.在△ABC中,∠A:∠B:∠C=2:3:4,求∠A、∠B、∠C的度数.
21.如图,在RT△ABC中,∠ACB=90°,∠B=35°,CD⊥AB,垂足为点D,
(1)求∠ACD的度数;
(2)找出图中相等的角,并说明理由.
22.如图,在△ABC中,∠ABC=∠ACB=∠BDC,∠A=∠DCA,求∠A的度数.
23.如图,在 ABC中,点、点分别为、上一点,平分,,.
(1)判断与的位置关系并说明理由;
(2)求的度数.
24.在一个三角形中,如果一个内角是另一个内角的3倍,这样的三角形我们称之为“三倍角三角形”,例如,三个内角分别为,,的三角形是“三倍角三角形”.
(1) ABC中,,, ABC是“三倍角三角形”吗?为什么?
(2)若 ABC是“三倍角三角形”,且,求 ABC中最小内角的度数.
25.【问题】
如图,在 ABC中,平分,平分,若,则____________;
若,则____________.
【探究】
()如图,在 ABC中,、三等分,、三等分,若,则____________;
()如图,是与外角的平分线和的交点,试分析和有怎样的关系?请说明理由;
()如图,是外角与外角的平分线和的交点,则与有怎样的关系?请说明理由.
答案
一、单选题
1.B
【分析】本题考查三角形的内角和定理,解题的关键是掌握三角形的内角和定理.利用三角形的内角和等于180度即可求解.
【解析】解:∵,,
∴,
故选B.
2.C
【分析】本题考查了三角形的外角性质.根据三角形的外角性质“三角形的外角大于任何一个不相邻的内角”即可得解.
【解析】解:∵是的一个外角,
∴,
故选:C.
3.B
【分析】本题主要考查了三角形外角的性质,先由平角的定义求出的度数,再由三角形外角的性质即可求出的度数.
【解析】解:∵,
∴,
∴,
故选:B.
4.C
【分析】依据三角形的外角与它相邻的内角互为邻补角,可判断出此三角形有一内角为钝角,从而得出这个三角形是钝角三角形.
【解析】解:∵三角形的一个外角与它相邻的内角和为,而这个外角小于它相邻的内角,
∴与它相邻的这个内角大于,
∴这个三角形是钝角三角形.
故选:C.
5.C
【分析】本题考查了三角形外角的性质,熟记这个知识点是解题的关键.三角形的一个外角等于和它不相邻的两个内角的和,由此求解.
【解析】解:,,
,
故选:C.
6.C
【分析】本题主要考查了三角形的内角和定理,直角三角形的性质等知识点,根据直角三角形的判定方法对各个选项进行分析判定即可得解,熟练掌握三角形的内角和定理,直角三角形的性质是解决此题的关键.
【解析】解:①∵,则,,∴是直角三角形,符合题意;
②∵,设,则,,,∴是直角三角形,符合题意;
③∵,∴,则,∴是直角三角形,符合题意;
④∵,则,∴为钝角三角形,不符合题意;
∴能确定为是直角三角形的有①②③,
故选:C.
7.B
【分析】此题主要考查了三角形内角和定理,熟练掌握三角形内角和定理是解决问题的关键.
先根据三角形内角和定理求出,然后在 ADE中利用三角形的内角和定理即可求出的度数.
【解析】解:在 ABC中,,,
,
在 ADE中,.
故选:B.
8.B
【分析】本题主要考查平行线的性质,由题意可得,,从而可求得,再由三角形的内角和可求得,利用三角形的外角性质即可求的度数.
【解析】解:如图,
由题意得:,,
∴,
∵,
∴,
∴,
∴,
故选:B.
9.B
【分析】根据三角形的内角和等于180°,用∠AGB表示出∠A,∠B,用∠EMF表示出∠E,∠F,用∠CND表示出∠C,∠D,然后再根据对顶角相等的性质解出它们的度数即可.
【解析】解:如图,
∵三角形的内角和等于180°,
∴∠A+∠B=180°-∠AGB,∠E+∠F=180°-∠EMF,∠C+∠D=180°-∠CND.
∵对顶角相等,
∴∠AGB=∠MGN,∠EMF=∠GMN,∠CND=∠MNG.
∵∠MGN+∠GMN+∠MNG=180°,
∴∠A+∠B+∠E+∠F+∠C+∠D
=180°-∠AGB+180°-∠EMF+180°-∠CND
=540°-(∠AGB+∠EMF+∠CND)
=540°-180°
=360°.
故选B
10.A
【分析】本题考查了三角形的外角性质,折叠的性质,设与交于点,由折叠性质可知,然后由三角形的外角性质得,,然后代入即可求解,掌握三角形的外角性质是解题的关键.
【解析】解:设与交于点,
由折叠得:,
∵是的外角,是的外角,
∴,,
∵,,,
∴,
故选:.
二、填空题
11. 1 1
【分析】根据三角形的内角和是180°可知,三角形的内角不可能存在两个(及以上)的直角和钝角.
【解析】解:∵如果三角形中由两个直角或钝角,那么该三角形的内角和就会大于180°,
∴在三角形的三个内角中,最多有1个直角,最多有1个钝角.
故答案为:1,1.
12. 锐角 钝角
【分析】根据三角形的内角和等于180°求出∠C,然后根据三角形的分类解答即可.
【解析】解:在△ABC中,
∵∠A=50°,∠B=55°,
∴∠C=75°,
∴三角形的三个内角都是锐角,
∴这个三角形就是锐角三角形.
∵∠A=50°,∠B=25°,
∴∠C=105°,
∴三角形有一个内角是钝角,
∴这个三角形就是钝角三角形.
故答案为:锐角,钝角
13.70
【分析】本题主要考查三角形的外角性质,直接利用三角形的外角性质进行求解即可.
【解析】解:∵是的外角,
∴,
故答案为:70.
14.
【分析】本题考查了三角形外角的性质,一元一次方程,解题关键是运用三角形一个外角等于与它不相邻的两个内角和得出关系式,由三角形外角性质可得结论.
【解析】∵三角形一个外角等于与它不相邻的两个内角和,
,
解得:,
故答案为:.
15.140°
【分析】根据∠B相邻的外角等于不相邻的两内角∠A、∠C的和解答即可.
【解析】解:∵与∠B相邻的外角等于140°,
∴∠A+∠C=140°.
故答案为:140°.
16.90
【分析】如图,由题意知∠1+∠2=3∠C①,由外角的性质得∠1=∠4+∠C,∠2=∠3+∠C,代入①整理即可.
【解析】解:如图,
∵∠A、∠B的外角之和等于∠C的3倍,
∴∠1+∠2=3∠C,
∵∠1=∠4+∠C,∠2=∠3+∠C,
∴∠4+∠C+∠3+∠C=3∠C,
∴2∠C=∠4+∠C+∠3=180°,
∴∠C=90°.
故答案为:90.
17.
【分析】本题考查三角形外角的性质及三角形的内角和定理,根据三角形的内角和定理以及三角形的外角的性质即可解决问题.
【解析】解:是 ABC的外角,,,
,
∵,
,
故答案为:45.
18.
【分析】本题考查矩形的性质、平行线的性质、折叠的性质、三角形外角的性质,
如图2,延长到点M,由折叠的性质可得,根据矩形的性质和平行线的性质得,再利用三角形外角的性质求得,如图3,由折叠的性质得,,再利用三角形外角的性质求解即可.
【解析】解:如图2,延长到点M,
由折叠的性质得,,
∵,
∴,
∴,
如图3,由折叠的性质得,,
∴,
故答案为:.
三、解答题
19.∵∠B-∠C=15°,
∴∠B=∠C+15°,
∵∠A+∠B+∠C=180°,
∴105°+∠C+15°+∠C=180°,
∴∠C=30°.
20.解:设∠A=2k,∠B=3k,∠C=4k,
2k+3k+4k=180,
解得k=20,
∴∠A=2k=40°、∠B=3k=60°、∠C=4k=80°.
21.解:(1)在Rt△ABC中,∵∠ACB=90°,∠B=35°,
∴∠A=180°-90°-35°=55°,
∵CD⊥AB,
∴∠BDC=∠ADC=90°,
∴∠ACD=180°-90°-55°=35°;
(2))∵CD⊥AB,
∴∠BDC=∠ADC=90°,
∴∠BDC=∠ADC=∠ACB;
∵∠B=35°,∠ACD=35°,
∴∠B=∠ACD;
∵∠A=55°,∠BCD=∠ACB -∠ACD=90°-35°=55°,
∴∠A=∠BCD.
∴图中相等的角有:∠BDC=∠ADC=∠ACB,∠B=∠ACD,∠A=∠BCD.
22.解:∵∠A=∠DCA,
∴∠BDC=2∠A,
∵∠ABC=∠ACB=∠BDC,
∴∠ABC=∠ACB=2∠A,
∵∠ABC+∠ACB+∠A=180°,
∴2∠A+2∠A+∠A=180°,
∴5∠A=180°,
∴∠A=36°.
23.(1)解:,理由如下:
∵平分,
∴,
∵,
∴,
∴;
(2)解:∵,,
∴,
∴,
∴.
24.(1)解: ABC是“三倍角三角形”,理由如下:
∵,,
∴,
∴ ABC是“三倍角三角形”.
(2)∵,
∴,
设最小的角为,
①当时,,满足题意;
②最小角为时,另外两个角为,,满足题意;
③当时,,,(不合题意,舍去)
答②: ABC中最小内角的度数为或.
25.解:问题:若,
则,
∵平分,平分,
∴ ,,
∴,
∴,
故答案为:;
若,
则,
∵平分,平分,
∴ ,,
∴,
∴,
故答案为:;
()如图,∵,
∴,
∵、三等分,、三等分,
∴,,
∴,
∴,
故答案为:;
().
理由:由三角形的外角性质得,,,
∵是与外角的平分线和的交点,
∴, ,
∴ ,
∴∠A=2∠BOC;
().
理由:∵是外角与外角的平分线和的交点,
∴,
,
在中,
,
,
∵,
∴.
一、单选题
1.在 ABC中,若,,则( )
A. B. C. D.
2.如图,与的大小关系是( )
A. B. C. D.不能确定
3.如图,若,则的度数为( )
A. B. C. D.
4.如果三角形的一个外角小于与它相邻的内角,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
5.如图,点在 ABC的边上,,,则的度数为( )
A. B. C. D.
6.在下列条件中:①,②,③,④中,能确定 ABC是直角三角形的条件有( )
A.1个 B.2个 C.3个 D.4个
7.如图,点E,D分别在,上,若,,则的度数为( )
A. B. C. D.
8.一把直尺与一块直角三角板如图方式摆放,若,则的度数是( )
A. B. C. D.
9.如图,∠A+∠B+∠C+∠D+∠E+∠F=( )
A.180° B.360° C.540° D.以上答案都不是
10.如图,将一张三角形纸片的一角折叠,使点落在 ABC外的处,折痕为.如果,,,那么下列式子中正确的是( )
A. B.
C. D.
二、填空题
11.在三角形的三个内角中,最多有 个直角,最多有 个钝角.
12.在△ABC中,若∠A=50°,∠B=55°,则△ABC是 三角形;若∠A=50°,∠B=25°,则△ABC是 三角形.(填“锐角”,“直角”或“钝角”)
13.如图,在 ABC中,,,则等于 度.
14.如图,图中的值为 .
15.在△ABC中,如果与∠B相邻的外角等于140°,那么∠A+∠C= .
16.在△ABC中,∠A、∠B的外角之和等于∠C的3倍,那么∠C= 度.
17.如图,点、、在同一条直线上,,,,则
18.如图1是长方形纸带,,将纸带沿折叠成图2,再沿折叠成图3,则图3中的的度数是 .
三、解答题
19.在△ABC中,已知∠A=105°,∠B-∠C=15°,求∠C的度数.
20.在△ABC中,∠A:∠B:∠C=2:3:4,求∠A、∠B、∠C的度数.
21.如图,在RT△ABC中,∠ACB=90°,∠B=35°,CD⊥AB,垂足为点D,
(1)求∠ACD的度数;
(2)找出图中相等的角,并说明理由.
22.如图,在△ABC中,∠ABC=∠ACB=∠BDC,∠A=∠DCA,求∠A的度数.
23.如图,在 ABC中,点、点分别为、上一点,平分,,.
(1)判断与的位置关系并说明理由;
(2)求的度数.
24.在一个三角形中,如果一个内角是另一个内角的3倍,这样的三角形我们称之为“三倍角三角形”,例如,三个内角分别为,,的三角形是“三倍角三角形”.
(1) ABC中,,, ABC是“三倍角三角形”吗?为什么?
(2)若 ABC是“三倍角三角形”,且,求 ABC中最小内角的度数.
25.【问题】
如图,在 ABC中,平分,平分,若,则____________;
若,则____________.
【探究】
()如图,在 ABC中,、三等分,、三等分,若,则____________;
()如图,是与外角的平分线和的交点,试分析和有怎样的关系?请说明理由;
()如图,是外角与外角的平分线和的交点,则与有怎样的关系?请说明理由.
答案
一、单选题
1.B
【分析】本题考查三角形的内角和定理,解题的关键是掌握三角形的内角和定理.利用三角形的内角和等于180度即可求解.
【解析】解:∵,,
∴,
故选B.
2.C
【分析】本题考查了三角形的外角性质.根据三角形的外角性质“三角形的外角大于任何一个不相邻的内角”即可得解.
【解析】解:∵是的一个外角,
∴,
故选:C.
3.B
【分析】本题主要考查了三角形外角的性质,先由平角的定义求出的度数,再由三角形外角的性质即可求出的度数.
【解析】解:∵,
∴,
∴,
故选:B.
4.C
【分析】依据三角形的外角与它相邻的内角互为邻补角,可判断出此三角形有一内角为钝角,从而得出这个三角形是钝角三角形.
【解析】解:∵三角形的一个外角与它相邻的内角和为,而这个外角小于它相邻的内角,
∴与它相邻的这个内角大于,
∴这个三角形是钝角三角形.
故选:C.
5.C
【分析】本题考查了三角形外角的性质,熟记这个知识点是解题的关键.三角形的一个外角等于和它不相邻的两个内角的和,由此求解.
【解析】解:,,
,
故选:C.
6.C
【分析】本题主要考查了三角形的内角和定理,直角三角形的性质等知识点,根据直角三角形的判定方法对各个选项进行分析判定即可得解,熟练掌握三角形的内角和定理,直角三角形的性质是解决此题的关键.
【解析】解:①∵,则,,∴是直角三角形,符合题意;
②∵,设,则,,,∴是直角三角形,符合题意;
③∵,∴,则,∴是直角三角形,符合题意;
④∵,则,∴为钝角三角形,不符合题意;
∴能确定为是直角三角形的有①②③,
故选:C.
7.B
【分析】此题主要考查了三角形内角和定理,熟练掌握三角形内角和定理是解决问题的关键.
先根据三角形内角和定理求出,然后在 ADE中利用三角形的内角和定理即可求出的度数.
【解析】解:在 ABC中,,,
,
在 ADE中,.
故选:B.
8.B
【分析】本题主要考查平行线的性质,由题意可得,,从而可求得,再由三角形的内角和可求得,利用三角形的外角性质即可求的度数.
【解析】解:如图,
由题意得:,,
∴,
∵,
∴,
∴,
∴,
故选:B.
9.B
【分析】根据三角形的内角和等于180°,用∠AGB表示出∠A,∠B,用∠EMF表示出∠E,∠F,用∠CND表示出∠C,∠D,然后再根据对顶角相等的性质解出它们的度数即可.
【解析】解:如图,
∵三角形的内角和等于180°,
∴∠A+∠B=180°-∠AGB,∠E+∠F=180°-∠EMF,∠C+∠D=180°-∠CND.
∵对顶角相等,
∴∠AGB=∠MGN,∠EMF=∠GMN,∠CND=∠MNG.
∵∠MGN+∠GMN+∠MNG=180°,
∴∠A+∠B+∠E+∠F+∠C+∠D
=180°-∠AGB+180°-∠EMF+180°-∠CND
=540°-(∠AGB+∠EMF+∠CND)
=540°-180°
=360°.
故选B
10.A
【分析】本题考查了三角形的外角性质,折叠的性质,设与交于点,由折叠性质可知,然后由三角形的外角性质得,,然后代入即可求解,掌握三角形的外角性质是解题的关键.
【解析】解:设与交于点,
由折叠得:,
∵是的外角,是的外角,
∴,,
∵,,,
∴,
故选:.
二、填空题
11. 1 1
【分析】根据三角形的内角和是180°可知,三角形的内角不可能存在两个(及以上)的直角和钝角.
【解析】解:∵如果三角形中由两个直角或钝角,那么该三角形的内角和就会大于180°,
∴在三角形的三个内角中,最多有1个直角,最多有1个钝角.
故答案为:1,1.
12. 锐角 钝角
【分析】根据三角形的内角和等于180°求出∠C,然后根据三角形的分类解答即可.
【解析】解:在△ABC中,
∵∠A=50°,∠B=55°,
∴∠C=75°,
∴三角形的三个内角都是锐角,
∴这个三角形就是锐角三角形.
∵∠A=50°,∠B=25°,
∴∠C=105°,
∴三角形有一个内角是钝角,
∴这个三角形就是钝角三角形.
故答案为:锐角,钝角
13.70
【分析】本题主要考查三角形的外角性质,直接利用三角形的外角性质进行求解即可.
【解析】解:∵是的外角,
∴,
故答案为:70.
14.
【分析】本题考查了三角形外角的性质,一元一次方程,解题关键是运用三角形一个外角等于与它不相邻的两个内角和得出关系式,由三角形外角性质可得结论.
【解析】∵三角形一个外角等于与它不相邻的两个内角和,
,
解得:,
故答案为:.
15.140°
【分析】根据∠B相邻的外角等于不相邻的两内角∠A、∠C的和解答即可.
【解析】解:∵与∠B相邻的外角等于140°,
∴∠A+∠C=140°.
故答案为:140°.
16.90
【分析】如图,由题意知∠1+∠2=3∠C①,由外角的性质得∠1=∠4+∠C,∠2=∠3+∠C,代入①整理即可.
【解析】解:如图,
∵∠A、∠B的外角之和等于∠C的3倍,
∴∠1+∠2=3∠C,
∵∠1=∠4+∠C,∠2=∠3+∠C,
∴∠4+∠C+∠3+∠C=3∠C,
∴2∠C=∠4+∠C+∠3=180°,
∴∠C=90°.
故答案为:90.
17.
【分析】本题考查三角形外角的性质及三角形的内角和定理,根据三角形的内角和定理以及三角形的外角的性质即可解决问题.
【解析】解:是 ABC的外角,,,
,
∵,
,
故答案为:45.
18.
【分析】本题考查矩形的性质、平行线的性质、折叠的性质、三角形外角的性质,
如图2,延长到点M,由折叠的性质可得,根据矩形的性质和平行线的性质得,再利用三角形外角的性质求得,如图3,由折叠的性质得,,再利用三角形外角的性质求解即可.
【解析】解:如图2,延长到点M,
由折叠的性质得,,
∵,
∴,
∴,
如图3,由折叠的性质得,,
∴,
故答案为:.
三、解答题
19.∵∠B-∠C=15°,
∴∠B=∠C+15°,
∵∠A+∠B+∠C=180°,
∴105°+∠C+15°+∠C=180°,
∴∠C=30°.
20.解:设∠A=2k,∠B=3k,∠C=4k,
2k+3k+4k=180,
解得k=20,
∴∠A=2k=40°、∠B=3k=60°、∠C=4k=80°.
21.解:(1)在Rt△ABC中,∵∠ACB=90°,∠B=35°,
∴∠A=180°-90°-35°=55°,
∵CD⊥AB,
∴∠BDC=∠ADC=90°,
∴∠ACD=180°-90°-55°=35°;
(2))∵CD⊥AB,
∴∠BDC=∠ADC=90°,
∴∠BDC=∠ADC=∠ACB;
∵∠B=35°,∠ACD=35°,
∴∠B=∠ACD;
∵∠A=55°,∠BCD=∠ACB -∠ACD=90°-35°=55°,
∴∠A=∠BCD.
∴图中相等的角有:∠BDC=∠ADC=∠ACB,∠B=∠ACD,∠A=∠BCD.
22.解:∵∠A=∠DCA,
∴∠BDC=2∠A,
∵∠ABC=∠ACB=∠BDC,
∴∠ABC=∠ACB=2∠A,
∵∠ABC+∠ACB+∠A=180°,
∴2∠A+2∠A+∠A=180°,
∴5∠A=180°,
∴∠A=36°.
23.(1)解:,理由如下:
∵平分,
∴,
∵,
∴,
∴;
(2)解:∵,,
∴,
∴,
∴.
24.(1)解: ABC是“三倍角三角形”,理由如下:
∵,,
∴,
∴ ABC是“三倍角三角形”.
(2)∵,
∴,
设最小的角为,
①当时,,满足题意;
②最小角为时,另外两个角为,,满足题意;
③当时,,,(不合题意,舍去)
答②: ABC中最小内角的度数为或.
25.解:问题:若,
则,
∵平分,平分,
∴ ,,
∴,
∴,
故答案为:;
若,
则,
∵平分,平分,
∴ ,,
∴,
∴,
故答案为:;
()如图,∵,
∴,
∵、三等分,、三等分,
∴,,
∴,
∴,
故答案为:;
().
理由:由三角形的外角性质得,,,
∵是与外角的平分线和的交点,
∴, ,
∴ ,
∴∠A=2∠BOC;
().
理由:∵是外角与外角的平分线和的交点,
∴,
,
在中,
,
,
∵,
∴.
同课章节目录
