10.2 一次函数和它的图象 第1课时 课件(共13张PPT) 青岛版八年级数学下册
文档属性
| 名称 | 10.2 一次函数和它的图象 第1课时 课件(共13张PPT) 青岛版八年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 17:49:27 | ||
图片预览




文档简介
(共13张PPT)
第十章 一次函数
10.2 一次函数和它的图象
第1课时
1.理解一次函数和正比例函数的概念,知道正比例函数是一次函数的特例;
2.能根据已知条件确定一次函数的表达式.
活动:和同伴一起交流,回答下列问题.
任务一:理解一次函数和正比例函数的概念.
一列高铁列车自北京站出发,运行10km后,便以300km∕h的速度匀速行驶.如果从运行10km后开始计时,请你写出该列车离开北京站的距离S
(单位:km)与时间t(单位:h)之间的函数表达式.
S=10+300t
思考:观察下面的函数表达式,说说它们有哪些共同特征?它们的一般形式是什么?
S=10+300t.
(1)y=2x-1; (2) ; (3) y=x-1;
(4) y=2x; (5)
共同特征: 1. 表达式都是自变量的一次式.
2. 都可以抽象成y=kx+b的形式 .
说说上面所举的函数中,k和b代表哪些数?
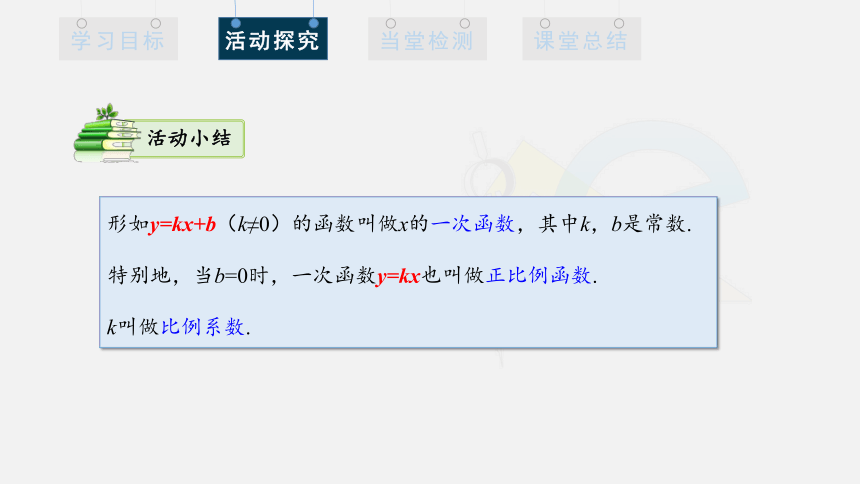
形如y=kx+b(k≠0)的函数叫做x的一次函数,其中k,b是常数.
特别地,当b=0时,一次函数y=kx也叫做正比例函数.
k叫做比例系数.
活动小结
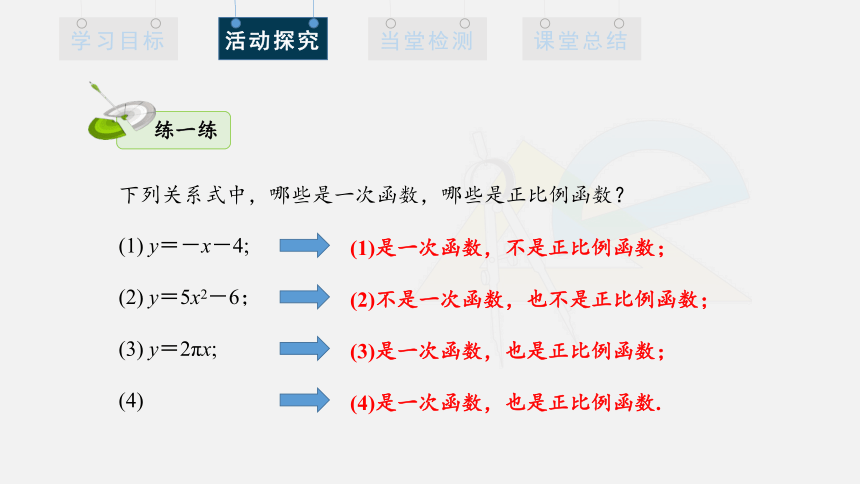
下列关系式中,哪些是一次函数,哪些是正比例函数?
(1) y=-x-4;
(2) y=5x2-6;
(3) y=2πx;
(4)
(1)是一次函数,不是正比例函数;
(2)不是一次函数,也不是正比例函数;
(3)是一次函数,也是正比例函数;
(4)是一次函数,也是正比例函数.
练一练
任务二:根据已知条件确定一次函数的表达式.
活动:阅读下列情境,回答问题.
情境1:铜的质量m(单位:g)与它的体积V(单位:cm3)是成正比例的量.当铜的体积V=3cm3时,测得它的质量是m=26.7g.
(1)求铜的质量m与体积V之间的函数表达式;
(2)当铜块的体积为2.5cm3时,求它的质量.
(2) 当V=2.5时,m=8.9×2.5=22.25.
∴当铜块的体积为2.5cm3时,铜块的质量为22.25g.
解:(1)∵m与V是成正比例的量,∴设m=kV,其中k为比例系数.
把V=3,m=26.7 代入 ,得 26.7=3k,解得k=8.9 .
∴质量m与体积V之间的函数表达式为m=8.9V(V>0).
情境2:小亮用如图的装置测定一根弹簧的长度与所挂重物间的函数关系,把弹簧的一端固定在铁架的横梁上,将刻度尺直立于铁架台上. 量出弹簧不挂任何重物时的长度 l0 . 在弹簧下端挂上一个钩码,待钩码静止后,量出弹簧的长度 l1 . 类似地,在弹簧的弹性限度内,依次量出弹簧下端挂 2 个、3 个、 、10 个钩码时,弹簧的长度 l2,l3, ,l10,并将得到的数据记录在下面的表格中:
钩码的个数 n / 个 0 1 2 3 4 5 6 7 8 9 10
弹簧长度 l / mm 120 125 130 135 140 145 150 155 160 165 170
(1)如果用n表示悬挂的钩码数量,l表示弹簧长度,在弹簧的弹性限度内,随着n的逐渐增加,l的变化趋势是什么?
(2)n每增加1个时,长度l伸长了多少?由此你能写出弹簧长度l与钩码个数n之间的函数表达式吗?l是n的一次函数吗?
解:(1)在弹簧的弹性限度内,当n逐渐增加时,l逐渐变大.
(2)从上表可知,在弹簧不挂钩码时,弹簧长度l0=120mm,当弹簧下端每增加1个钩码,弹簧长度l均增加5mm.所以弹簧长度l与钩码个数n之间函数的表达式是l=120+5n,由此可知,在弹性限度内,弹簧长度l是钩码个数n的一次函数.
钩码的个数 n / 个 0 1 2 3 4 5 6 7 8 9 10
弹簧长度 l / mm 120 125 130 135 140 145 150 155 160 165 170
C
1.下列函数中,y是x的正比例函数的是( )
A.y=4x+1 B.y=2x
C.y=-x D.
选项中y=4x+1是一次函数,不是正比例函数;y=2x , ,自变量的次数不为1;y=-x符合正比例函数的定义.
2.写出下列y与x的关系式,并判断:是否为一次函数?是否为正比例函数?
(1)正方形周长y与它的边长x的关系;
(2)一棵树的高度为60cm,每个月长高3cm,x月后这棵树的高度为y cm;
(3)正方形的面积y与它的边长x的关系.
解:(1)正方形周长为4倍的边长,则:y=4x,
y是x的正比例函数,也是一次函数.
(2)由题可知:y=60+3x,y是x的一次函数,但不是正比例函数.
(3)正方形面积为边长的平方,则:y=x2,
y不是x的一次函数,也不是正比例函数.
针对本课关键词“一次函数”,说说你学到了什么?
一次函数和正比例函数的概念
根据已知条件确定一次函数的表达式
一次函数与正比例函数
第十章 一次函数
10.2 一次函数和它的图象
第1课时
1.理解一次函数和正比例函数的概念,知道正比例函数是一次函数的特例;
2.能根据已知条件确定一次函数的表达式.
活动:和同伴一起交流,回答下列问题.
任务一:理解一次函数和正比例函数的概念.
一列高铁列车自北京站出发,运行10km后,便以300km∕h的速度匀速行驶.如果从运行10km后开始计时,请你写出该列车离开北京站的距离S
(单位:km)与时间t(单位:h)之间的函数表达式.
S=10+300t
思考:观察下面的函数表达式,说说它们有哪些共同特征?它们的一般形式是什么?
S=10+300t.
(1)y=2x-1; (2) ; (3) y=x-1;
(4) y=2x; (5)
共同特征: 1. 表达式都是自变量的一次式.
2. 都可以抽象成y=kx+b的形式 .
说说上面所举的函数中,k和b代表哪些数?
形如y=kx+b(k≠0)的函数叫做x的一次函数,其中k,b是常数.
特别地,当b=0时,一次函数y=kx也叫做正比例函数.
k叫做比例系数.
活动小结
下列关系式中,哪些是一次函数,哪些是正比例函数?
(1) y=-x-4;
(2) y=5x2-6;
(3) y=2πx;
(4)
(1)是一次函数,不是正比例函数;
(2)不是一次函数,也不是正比例函数;
(3)是一次函数,也是正比例函数;
(4)是一次函数,也是正比例函数.
练一练
任务二:根据已知条件确定一次函数的表达式.
活动:阅读下列情境,回答问题.
情境1:铜的质量m(单位:g)与它的体积V(单位:cm3)是成正比例的量.当铜的体积V=3cm3时,测得它的质量是m=26.7g.
(1)求铜的质量m与体积V之间的函数表达式;
(2)当铜块的体积为2.5cm3时,求它的质量.
(2) 当V=2.5时,m=8.9×2.5=22.25.
∴当铜块的体积为2.5cm3时,铜块的质量为22.25g.
解:(1)∵m与V是成正比例的量,∴设m=kV,其中k为比例系数.
把V=3,m=26.7 代入 ,得 26.7=3k,解得k=8.9 .
∴质量m与体积V之间的函数表达式为m=8.9V(V>0).
情境2:小亮用如图的装置测定一根弹簧的长度与所挂重物间的函数关系,把弹簧的一端固定在铁架的横梁上,将刻度尺直立于铁架台上. 量出弹簧不挂任何重物时的长度 l0 . 在弹簧下端挂上一个钩码,待钩码静止后,量出弹簧的长度 l1 . 类似地,在弹簧的弹性限度内,依次量出弹簧下端挂 2 个、3 个、 、10 个钩码时,弹簧的长度 l2,l3, ,l10,并将得到的数据记录在下面的表格中:
钩码的个数 n / 个 0 1 2 3 4 5 6 7 8 9 10
弹簧长度 l / mm 120 125 130 135 140 145 150 155 160 165 170
(1)如果用n表示悬挂的钩码数量,l表示弹簧长度,在弹簧的弹性限度内,随着n的逐渐增加,l的变化趋势是什么?
(2)n每增加1个时,长度l伸长了多少?由此你能写出弹簧长度l与钩码个数n之间的函数表达式吗?l是n的一次函数吗?
解:(1)在弹簧的弹性限度内,当n逐渐增加时,l逐渐变大.
(2)从上表可知,在弹簧不挂钩码时,弹簧长度l0=120mm,当弹簧下端每增加1个钩码,弹簧长度l均增加5mm.所以弹簧长度l与钩码个数n之间函数的表达式是l=120+5n,由此可知,在弹性限度内,弹簧长度l是钩码个数n的一次函数.
钩码的个数 n / 个 0 1 2 3 4 5 6 7 8 9 10
弹簧长度 l / mm 120 125 130 135 140 145 150 155 160 165 170
C
1.下列函数中,y是x的正比例函数的是( )
A.y=4x+1 B.y=2x
C.y=-x D.
选项中y=4x+1是一次函数,不是正比例函数;y=2x , ,自变量的次数不为1;y=-x符合正比例函数的定义.
2.写出下列y与x的关系式,并判断:是否为一次函数?是否为正比例函数?
(1)正方形周长y与它的边长x的关系;
(2)一棵树的高度为60cm,每个月长高3cm,x月后这棵树的高度为y cm;
(3)正方形的面积y与它的边长x的关系.
解:(1)正方形周长为4倍的边长,则:y=4x,
y是x的正比例函数,也是一次函数.
(2)由题可知:y=60+3x,y是x的一次函数,但不是正比例函数.
(3)正方形面积为边长的平方,则:y=x2,
y不是x的一次函数,也不是正比例函数.
针对本课关键词“一次函数”,说说你学到了什么?
一次函数和正比例函数的概念
根据已知条件确定一次函数的表达式
一次函数与正比例函数
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
