11.1 图形的平移 第2课时 课件(共11张PPT)2024-2025学年青岛版八年级数学下册
文档属性
| 名称 | 11.1 图形的平移 第2课时 课件(共11张PPT)2024-2025学年青岛版八年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 18:15:16 | ||
图片预览




文档简介
(共11张PPT)
第十一章 图形的平移与旋转
11.1 图形的平移
第2课时
1.掌握画平移图形的一般步骤;
2.能运用平移的概念与基本性质解决有关几何问题.
活动1:小组合作讨论,完成下列问题.
任务一:运用平移的概念与基本性质解决有关几何问题.
如图,任意剪一张平行四边形纸片ABCD,设∠B<90°.在边BC上取一点E,连接AE,沿AE将ΔABE剪下,将它沿边AD向右平移,平移距离等于AD的长.
(1)试判断平移后所得到的四边形AEFD的形状,并说明理由;
(2)四边形AEFD能否是矩形?如果能,AE应满足什么条件?
如果不能,请说明理由;
(3)四边形AEFD能否是菱形?如果能,AD应满足什么条件?
如果不能,请说明理由.
(1)试判断平移后所得到的四边形AEFD的形状,并说明理由;
解:四边形AEFD是平行四边形.
在上述平移过程中,A与D,B与C,E与F分别是对应点,点B,E,C,F在同一条直线上.
根据平移的性质,AD∥EF且AD=EF,∴四边形AEFD是平行四边形.
(2)四边形AEFD能否是矩形?如果能,AE应满足什么条件?如果不能,请说明理由;
解:由∠B<90°,过点A作AE⊥BC,垂足为E,
点E在线段BC上.平移ΔABE所得到的
平行四边形AEFD是矩形.
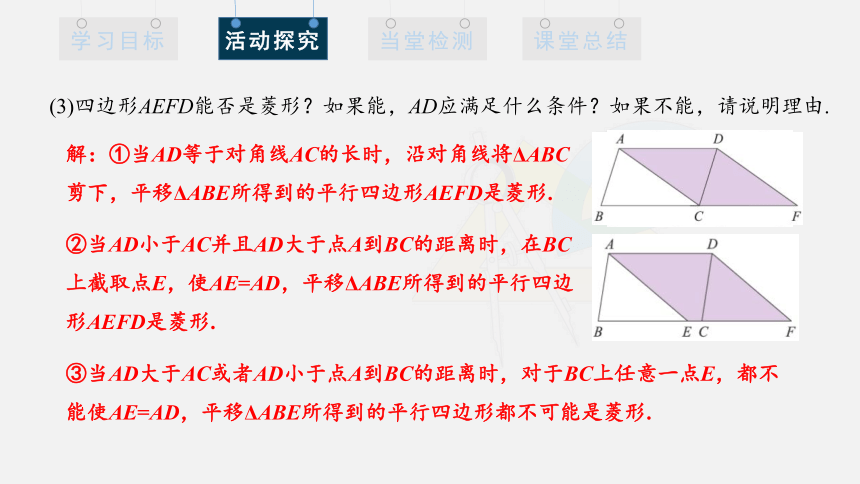
解:①当AD等于对角线AC的长时,沿对角线将ΔABC剪下,平移ΔABE所得到的平行四边形AEFD是菱形.
(3)四边形AEFD能否是菱形?如果能,AD应满足什么条件?如果不能,请说明理由.
②当AD小于AC并且AD大于点A到BC的距离时,在BC上截取点E,使AE=AD,平移ΔABE所得到的平行四边形AEFD是菱形.
③当AD大于AC或者AD小于点A到BC的距离时,对于BC上任意一点E,都不能使AE=AD,平移ΔABE所得到的平行四边形都不可能是菱形.
任务二:掌握画平移图形的一般步骤.
活动:动手画图,并尝试总结画平移图形的一般步骤.
如图,平移四边形ABCD,使点A移动到点A',画出平移后的四边形A'B'C'D'.
B'
C'
D'
解:如图所示:
(1)连接AA';
(2)过点B作AA'的平行线l,在l上截取BB'=AA',得到B的对应点B';
(3)同理,分别作C、D的对应点C'、 D' ;
(4)连接A'B',B'C',C'D', D'A' ,四边形A'B'C'D'为所求.
活动小结
平移作图的步骤:
(1)确定平移的方向和距离;
(2)根据平移的性质作出图形上各关键点的对应点;
(3)依次连接各关键点的对应点.
1.在下图的方格纸中将小船中的点A移到点A',作出平移后的小船.
解:如图:
2.如图①,A′是矩形ABCD边AD上一点.把ABCD沿对角线AC剪开,然后把ΔABC沿AD向右平移,平移距离等于AA′的长,得到ΔA′B′C′(图②).设A′B′交AC于点E,A′C′交CD于点F,是判断ΔA′DF与ΔCB′E是否相等,请说明理由.
解:ΔA′DF≌ΔCB′E.
∵ΔA′B′C′是ΔABC沿AD向右平移得到,
又∵AB∥CD,∴A′B′∥CD.
∴A′B′∥AB,A′C′∥AC.
∴四边形A′ECF是平行四边形.∴A′F=CE,A′E=CF.
2.如图①,A′是矩形ABCD边AD上一点.把ABCD沿对角线AC剪开,然后把ΔABC沿AD向右平移,平移距离等于AA′的长,得到ΔA′B′C′(图②).设A′B′交AC于点E,A′C′交CD于点F,是判断ΔA′DF与ΔCB′E是否相等,请说明理由.
∵A′B′=CD,∴B′E′=DF.
又∵∠D=90°,而A′B′∥AB,
∴∠CB′E=∠B=90°.
∴RtΔA′DF≌RtΔCB′E.
针对本课关键词“图形的平移”,回答下列问题.
平移作图的一般步骤是什么?
第十一章 图形的平移与旋转
11.1 图形的平移
第2课时
1.掌握画平移图形的一般步骤;
2.能运用平移的概念与基本性质解决有关几何问题.
活动1:小组合作讨论,完成下列问题.
任务一:运用平移的概念与基本性质解决有关几何问题.
如图,任意剪一张平行四边形纸片ABCD,设∠B<90°.在边BC上取一点E,连接AE,沿AE将ΔABE剪下,将它沿边AD向右平移,平移距离等于AD的长.
(1)试判断平移后所得到的四边形AEFD的形状,并说明理由;
(2)四边形AEFD能否是矩形?如果能,AE应满足什么条件?
如果不能,请说明理由;
(3)四边形AEFD能否是菱形?如果能,AD应满足什么条件?
如果不能,请说明理由.
(1)试判断平移后所得到的四边形AEFD的形状,并说明理由;
解:四边形AEFD是平行四边形.
在上述平移过程中,A与D,B与C,E与F分别是对应点,点B,E,C,F在同一条直线上.
根据平移的性质,AD∥EF且AD=EF,∴四边形AEFD是平行四边形.
(2)四边形AEFD能否是矩形?如果能,AE应满足什么条件?如果不能,请说明理由;
解:由∠B<90°,过点A作AE⊥BC,垂足为E,
点E在线段BC上.平移ΔABE所得到的
平行四边形AEFD是矩形.
解:①当AD等于对角线AC的长时,沿对角线将ΔABC剪下,平移ΔABE所得到的平行四边形AEFD是菱形.
(3)四边形AEFD能否是菱形?如果能,AD应满足什么条件?如果不能,请说明理由.
②当AD小于AC并且AD大于点A到BC的距离时,在BC上截取点E,使AE=AD,平移ΔABE所得到的平行四边形AEFD是菱形.
③当AD大于AC或者AD小于点A到BC的距离时,对于BC上任意一点E,都不能使AE=AD,平移ΔABE所得到的平行四边形都不可能是菱形.
任务二:掌握画平移图形的一般步骤.
活动:动手画图,并尝试总结画平移图形的一般步骤.
如图,平移四边形ABCD,使点A移动到点A',画出平移后的四边形A'B'C'D'.
B'
C'
D'
解:如图所示:
(1)连接AA';
(2)过点B作AA'的平行线l,在l上截取BB'=AA',得到B的对应点B';
(3)同理,分别作C、D的对应点C'、 D' ;
(4)连接A'B',B'C',C'D', D'A' ,四边形A'B'C'D'为所求.
活动小结
平移作图的步骤:
(1)确定平移的方向和距离;
(2)根据平移的性质作出图形上各关键点的对应点;
(3)依次连接各关键点的对应点.
1.在下图的方格纸中将小船中的点A移到点A',作出平移后的小船.
解:如图:
2.如图①,A′是矩形ABCD边AD上一点.把ABCD沿对角线AC剪开,然后把ΔABC沿AD向右平移,平移距离等于AA′的长,得到ΔA′B′C′(图②).设A′B′交AC于点E,A′C′交CD于点F,是判断ΔA′DF与ΔCB′E是否相等,请说明理由.
解:ΔA′DF≌ΔCB′E.
∵ΔA′B′C′是ΔABC沿AD向右平移得到,
又∵AB∥CD,∴A′B′∥CD.
∴A′B′∥AB,A′C′∥AC.
∴四边形A′ECF是平行四边形.∴A′F=CE,A′E=CF.
2.如图①,A′是矩形ABCD边AD上一点.把ABCD沿对角线AC剪开,然后把ΔABC沿AD向右平移,平移距离等于AA′的长,得到ΔA′B′C′(图②).设A′B′交AC于点E,A′C′交CD于点F,是判断ΔA′DF与ΔCB′E是否相等,请说明理由.
∵A′B′=CD,∴B′E′=DF.
又∵∠D=90°,而A′B′∥AB,
∴∠CB′E=∠B=90°.
∴RtΔA′DF≌RtΔCB′E.
针对本课关键词“图形的平移”,回答下列问题.
平移作图的一般步骤是什么?
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
