第11章 图形的平移与旋转 综合与实践 哪条路径最短 课件(共13张PPT)2024-2025学年青岛版八年级数学下册
文档属性
| 名称 | 第11章 图形的平移与旋转 综合与实践 哪条路径最短 课件(共13张PPT)2024-2025学年青岛版八年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 18:22:15 | ||
图片预览




文档简介
(共13张PPT)
综合与实践
哪条路径最短
1.学会利用轴对称及平移等图形变换解决最短路径问题.
活动1:小组合作讨论,完成下列问题.
任务一:解决最短路径问题.
问题1:在七(上),我们曾遇到这样一个实际问题:如图,l表示一条河流,A,B是两个村庄,现准备在河上建一座桥.在哪里建桥可使A,B两村之间的路径最短呢?
B
l
A
C
解析:连接A,B两点,交直线l于点C,则点C即为所求的位置,可以使得AC+BC的值最小.
依据:两点之间,线段最短.
问题2:前面的问题1属于河流很窄,宽度可以忽略不计的情况.如果河流较宽,河的两岸互相平行,要在河上修建一座与河岸垂直的桥梁CD,在哪里建桥可使A,B两村之间的路径A-C-D-B最短?
A
B
小亮的方案如下:连接AB,交l1与点C,过点C作CD⊥l2,垂足为D.连接BD,则在点C处所见的垂直于河岸的桥梁CD是最佳的建桥方案.
你同意他的说法吗?
C
D
l1
l2
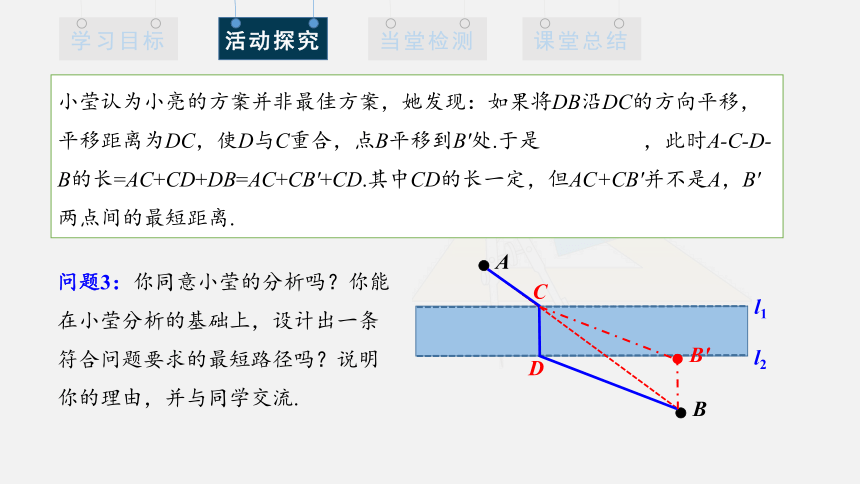
小莹认为小亮的方案并非最佳方案,她发现:如果将DB沿DC的方向平移,平移距离为DC,使D与C重合,点B平移到B′处.于是 ,此时A-C-D-B的长=AC+CD+DB=AC+CB′+CD.其中CD的长一定,但AC+CB′并不是A,B′两点间的最短距离.
A
B
C
D
l1
l2
B′
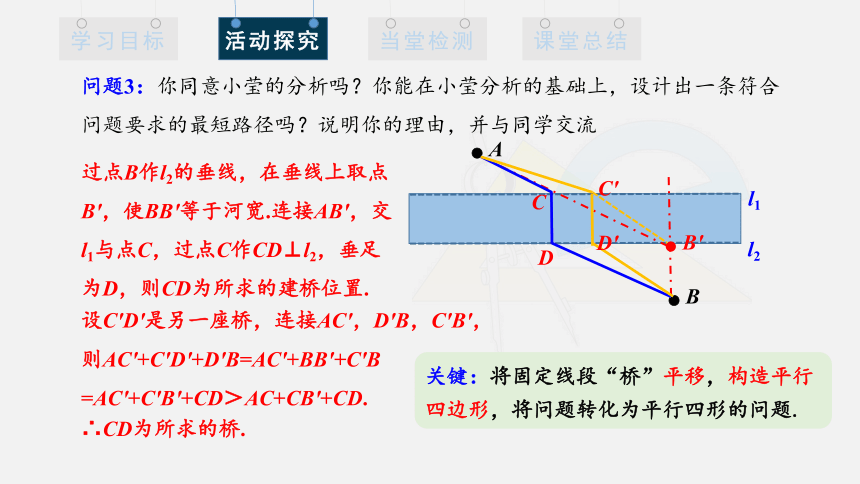
问题3:你同意小莹的分析吗?你能在小莹分析的基础上,设计出一条符合问题要求的最短路径吗?说明你的理由,并与同学交流.
A
B
过点B作l2的垂线,在垂线上取点B′,使BB′等于河宽.连接AB′,交l1与点C,过点C作CD⊥l2,垂足为D,则CD为所求的建桥位置.
C
D
设C′D′是另一座桥,连接AC′,D′B,C′B′,
则AC′+C′D′+D′B=AC′+BB′+C′B
=AC′+C′B′+CD>AC+CB′+CD.
B′
∴CD为所求的桥.
l1
l2
C′
D′
关键:将固定线段“桥”平移,构造平行四边形,将问题转化为平行四形的问题.
问题3:你同意小莹的分析吗?你能在小莹分析的基础上,设计出一条符合问题要求的最短路径吗?说明你的理由,并与同学交流
活动2:和同伴一起交流,完成下列问题.
B
l
A
C
A
B
l
数学问题
抽象成
实际问题
问题1:你还记得八(上)的将军饮马的故事吗?将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的B地开会,应该怎样走才能使路程最短?
将这则故事转化为数学问题,就是在 l 上确定一点 C,使路径A—C—B最短
B′
A
B
l
C
作法:利用轴对称,作出点B关于直线l的对称点B′.连接AB′交直线l于点C,则点C即为所求.
问题1:你还记得八(上)的将军饮马的故事吗?将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的B地开会,应该怎样走才能使路程最短?
问题2:如图,在河岸的同侧新建两个居民小区,现计划沿河岸修建一条长为s的绿化带CD(宽度不计),供小区的居民散步使用,当CD选在何处时,路径AC与BD的和最小?
B
·
A
l
·
D
A′
A1
s
C
s
B′
B1
将点A向右平移长度s,得点A1.
设B1为B关于l的轴对称点,连A1B1,交l与点D,在l上点D的左侧取点C,使CD=s,则CD为所求.
为了证明CD符合要求,可在l上任取C′,D′,使 C′D′=s,证明AC′+BD′>AC+BD.
活动小结
点在直线同侧
两点一线型
点在直线异侧
B
l
A
C
最短路径问题:
B′
A
B
l
C
活动3:阅读课本P197中的问题(4)-问题(6),完成下列问题.
问题:由(5)(6)的结果你有什么发现?设 AB = a,点 A,B 到直线 l 的距离分别是 n,m(0 < n < m),根据 a 与 m,n 三个数据之间的关系,你能分情况算出他们二人设计的方案中,哪个更节省吗?
设d1,d2分别代表小亮、小莹方案中铺设的管道长度.
①当a<2m- 时,d1>d2;②当a=2m- 时,d1=d2;③当a>2m- 时,d1<d2.
1.如图,在∠AOB内部有两点M、N,是否在OA、OB上分别存在点E、F,使得E、F、M、N,四点组成的四边形的周长最短,找出E、F两点.
针对本课关键词“哪条路径最短”,说说你学到了哪些知识.
综合与实践
哪条路径最短
1.学会利用轴对称及平移等图形变换解决最短路径问题.
活动1:小组合作讨论,完成下列问题.
任务一:解决最短路径问题.
问题1:在七(上),我们曾遇到这样一个实际问题:如图,l表示一条河流,A,B是两个村庄,现准备在河上建一座桥.在哪里建桥可使A,B两村之间的路径最短呢?
B
l
A
C
解析:连接A,B两点,交直线l于点C,则点C即为所求的位置,可以使得AC+BC的值最小.
依据:两点之间,线段最短.
问题2:前面的问题1属于河流很窄,宽度可以忽略不计的情况.如果河流较宽,河的两岸互相平行,要在河上修建一座与河岸垂直的桥梁CD,在哪里建桥可使A,B两村之间的路径A-C-D-B最短?
A
B
小亮的方案如下:连接AB,交l1与点C,过点C作CD⊥l2,垂足为D.连接BD,则在点C处所见的垂直于河岸的桥梁CD是最佳的建桥方案.
你同意他的说法吗?
C
D
l1
l2
小莹认为小亮的方案并非最佳方案,她发现:如果将DB沿DC的方向平移,平移距离为DC,使D与C重合,点B平移到B′处.于是 ,此时A-C-D-B的长=AC+CD+DB=AC+CB′+CD.其中CD的长一定,但AC+CB′并不是A,B′两点间的最短距离.
A
B
C
D
l1
l2
B′
问题3:你同意小莹的分析吗?你能在小莹分析的基础上,设计出一条符合问题要求的最短路径吗?说明你的理由,并与同学交流.
A
B
过点B作l2的垂线,在垂线上取点B′,使BB′等于河宽.连接AB′,交l1与点C,过点C作CD⊥l2,垂足为D,则CD为所求的建桥位置.
C
D
设C′D′是另一座桥,连接AC′,D′B,C′B′,
则AC′+C′D′+D′B=AC′+BB′+C′B
=AC′+C′B′+CD>AC+CB′+CD.
B′
∴CD为所求的桥.
l1
l2
C′
D′
关键:将固定线段“桥”平移,构造平行四边形,将问题转化为平行四形的问题.
问题3:你同意小莹的分析吗?你能在小莹分析的基础上,设计出一条符合问题要求的最短路径吗?说明你的理由,并与同学交流
活动2:和同伴一起交流,完成下列问题.
B
l
A
C
A
B
l
数学问题
抽象成
实际问题
问题1:你还记得八(上)的将军饮马的故事吗?将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的B地开会,应该怎样走才能使路程最短?
将这则故事转化为数学问题,就是在 l 上确定一点 C,使路径A—C—B最短
B′
A
B
l
C
作法:利用轴对称,作出点B关于直线l的对称点B′.连接AB′交直线l于点C,则点C即为所求.
问题1:你还记得八(上)的将军饮马的故事吗?将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的B地开会,应该怎样走才能使路程最短?
问题2:如图,在河岸的同侧新建两个居民小区,现计划沿河岸修建一条长为s的绿化带CD(宽度不计),供小区的居民散步使用,当CD选在何处时,路径AC与BD的和最小?
B
·
A
l
·
D
A′
A1
s
C
s
B′
B1
将点A向右平移长度s,得点A1.
设B1为B关于l的轴对称点,连A1B1,交l与点D,在l上点D的左侧取点C,使CD=s,则CD为所求.
为了证明CD符合要求,可在l上任取C′,D′,使 C′D′=s,证明AC′+BD′>AC+BD.
活动小结
点在直线同侧
两点一线型
点在直线异侧
B
l
A
C
最短路径问题:
B′
A
B
l
C
活动3:阅读课本P197中的问题(4)-问题(6),完成下列问题.
问题:由(5)(6)的结果你有什么发现?设 AB = a,点 A,B 到直线 l 的距离分别是 n,m(0 < n < m),根据 a 与 m,n 三个数据之间的关系,你能分情况算出他们二人设计的方案中,哪个更节省吗?
设d1,d2分别代表小亮、小莹方案中铺设的管道长度.
①当a<2m- 时,d1>d2;②当a=2m- 时,d1=d2;③当a>2m- 时,d1<d2.
1.如图,在∠AOB内部有两点M、N,是否在OA、OB上分别存在点E、F,使得E、F、M、N,四点组成的四边形的周长最短,找出E、F两点.
针对本课关键词“哪条路径最短”,说说你学到了哪些知识.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
