广东省深圳大学附属实验中学2024-2025学年高二下学期第一次段考数学试题(PDF版,含答案)
文档属性
| 名称 | 广东省深圳大学附属实验中学2024-2025学年高二下学期第一次段考数学试题(PDF版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 10:20:36 | ||
图片预览




文档简介
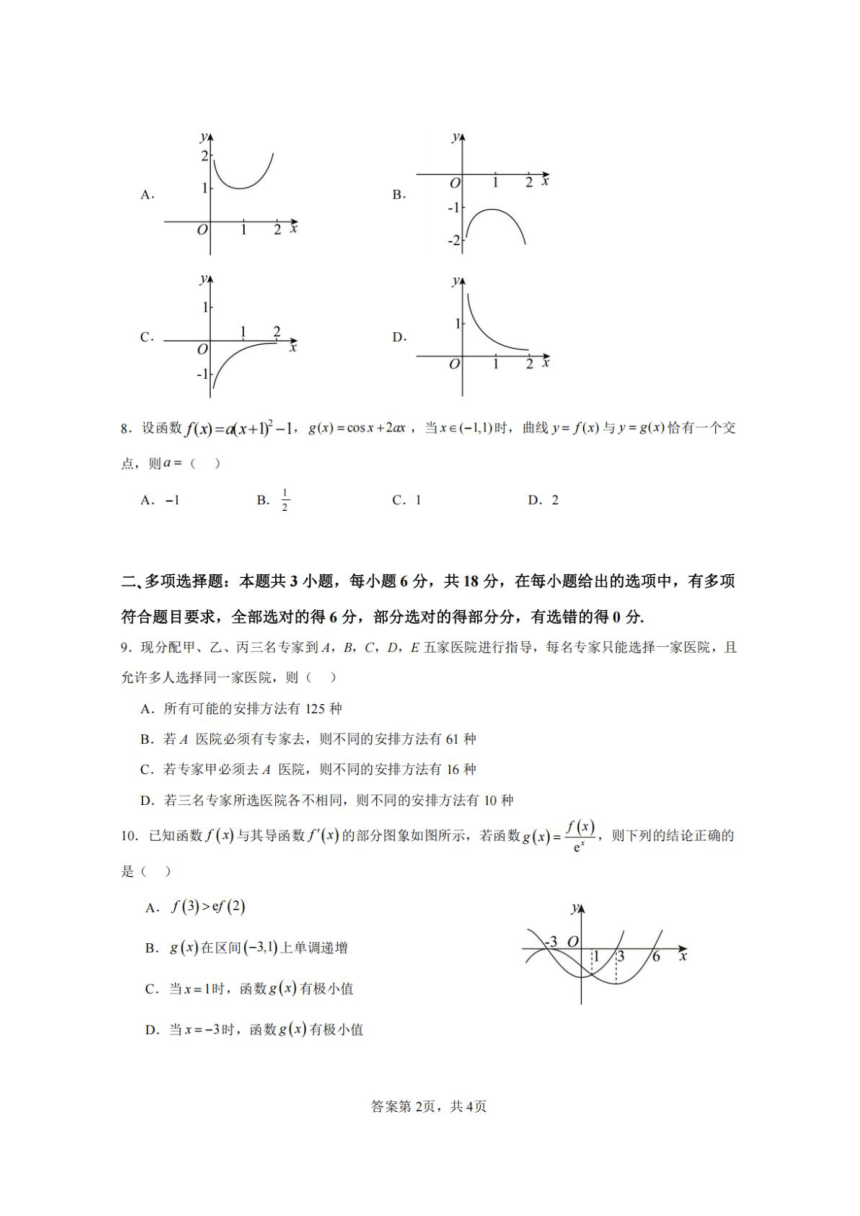
注意到F(x),G(x)均为偶函数,可知该交点只能在y轴上,
可得F(0=G(0),即a-1=1,解得a=2,
若a=2,令F(x)=G(x),可得2x2+1-cosx=0
因为x∈(-1,1),则2x2≥0,1-cosx≥0,当且仅当x=0时,等号成立,
可得2x2+1-c0sx≥0,当且仅当x=0时,等号成立,
则方程2x2+1-cosx=0有且仅有一个实根0,即曲线y=F(x)与y=G(x)恰有一个交点,
所以a=2符合题意;
解法二:令h(x)=f(x)-g(x)=2+a-1-COSx,x∈(-1,1),
原题意等价于(x)有且仅有一个零点,
因为h(-x)=a(-x)+a-1-cos(-x)=ax2+a-1-cosx=h(x),则h(x)为偶函数,
根据偶函数的对称性可知h(x)的零点只能为0,
即h(0)=a-2=0,解得a=2,
若a=2,则h(x)=2x2+1-cosx,x∈(-1,),
又因为2x2≥0,1-cosx≥0当且仅当x=0时,等号成立,
可得h(x)≥0,当且仅当x=0时,等号成立,
即h(x)有且仅有一个零点0,所以a=2符合题意:
9.AB
【详解】对于A,每名专家有5种选择方法,则所有可能的安排方法有53=125种,A正确:
对于B,由选项A知,所有可能的方法有53种,A医院没有专家去的方法有43种,
所以A医院必须有专家去的不同的安排方法有53-4=61种,B正确:
对于C,专家甲必须去A医院,则专家乙、丙的安排方法有52=25种,C错误;
对于D,三名专家所选医院各不相同的安排方法有A=60种,D错误.
10.AC【详解】
由g)=四有g))-f),
er
6
由图可知∫(x),∫'(x)的分布如图所示:
y(x
f(x)
答案第3页,共8页
当10,所以g()>0,所以g(x)在(1,6)单调递增,
所以g()>g2),即)、),所以了6)>y(2),故A正确:
e3
当-3当x=1时,'(x)=f(x),所以g(x)=0,由图可知当-3当10,
所以g(x)在(-3,)单调递减,在(1,3)单调递增,所以x=1是g(x)的极小值点,
故当x=1时,函数g(x)有极小值,故C正确:
当x=-3时,'(x)=f(x),所以g(x)=0,由图可知当x<-3时,f'(x)>0>f(x),
所以∫"(x)-f(x)>0,所以g(x)>0,所以g(x)在(-∞,-3)单调递增,
所以当x=-3时,函数g(x)有极大值,故D错误,
故选:AC
11.AC【详解】对于A,因为an1+an-1=2an(n≥2),所以4n1-an=an-an-1,
所以数列{an}是等差数列,设公差为d,
因为a1=2,43=8,所以2d=8-2=6,解得d=3,
所以a,=4+(n-d=3n-S+3r2十”正确
2
对于B,因为4=2,6=2b,所以=2,所以数列{b,}是公比为2的等比数列,
b.
所以bn=bq-=2×2-=2”,所以Cn=46=3bn-1=32”-1,
所以Tn=3
21-2")
2-n=3.2*l-n-6,错误.
1-2
对于C,由B知Tn=3.2"-n-6,
所以T1-T=32m2-32m-1=32”-1>0恒成立,所以数列{亿}单调递增,
当n=8时,T=32°-8-6=1522<2025,
当n=9时,T,=320-9-6=3057>2025,
所以n的最大值为8,正确;
答案第4页,共8页
可得F(0=G(0),即a-1=1,解得a=2,
若a=2,令F(x)=G(x),可得2x2+1-cosx=0
因为x∈(-1,1),则2x2≥0,1-cosx≥0,当且仅当x=0时,等号成立,
可得2x2+1-c0sx≥0,当且仅当x=0时,等号成立,
则方程2x2+1-cosx=0有且仅有一个实根0,即曲线y=F(x)与y=G(x)恰有一个交点,
所以a=2符合题意;
解法二:令h(x)=f(x)-g(x)=2+a-1-COSx,x∈(-1,1),
原题意等价于(x)有且仅有一个零点,
因为h(-x)=a(-x)+a-1-cos(-x)=ax2+a-1-cosx=h(x),则h(x)为偶函数,
根据偶函数的对称性可知h(x)的零点只能为0,
即h(0)=a-2=0,解得a=2,
若a=2,则h(x)=2x2+1-cosx,x∈(-1,),
又因为2x2≥0,1-cosx≥0当且仅当x=0时,等号成立,
可得h(x)≥0,当且仅当x=0时,等号成立,
即h(x)有且仅有一个零点0,所以a=2符合题意:
9.AB
【详解】对于A,每名专家有5种选择方法,则所有可能的安排方法有53=125种,A正确:
对于B,由选项A知,所有可能的方法有53种,A医院没有专家去的方法有43种,
所以A医院必须有专家去的不同的安排方法有53-4=61种,B正确:
对于C,专家甲必须去A医院,则专家乙、丙的安排方法有52=25种,C错误;
对于D,三名专家所选医院各不相同的安排方法有A=60种,D错误.
10.AC【详解】
由g)=四有g))-f),
er
6
由图可知∫(x),∫'(x)的分布如图所示:
y(x
f(x)
答案第3页,共8页
当1
所以g()>g2),即)、),所以了6)>y(2),故A正确:
e3
当-3
所以g(x)在(-3,)单调递减,在(1,3)单调递增,所以x=1是g(x)的极小值点,
故当x=1时,函数g(x)有极小值,故C正确:
当x=-3时,'(x)=f(x),所以g(x)=0,由图可知当x<-3时,f'(x)>0>f(x),
所以∫"(x)-f(x)>0,所以g(x)>0,所以g(x)在(-∞,-3)单调递增,
所以当x=-3时,函数g(x)有极大值,故D错误,
故选:AC
11.AC【详解】对于A,因为an1+an-1=2an(n≥2),所以4n1-an=an-an-1,
所以数列{an}是等差数列,设公差为d,
因为a1=2,43=8,所以2d=8-2=6,解得d=3,
所以a,=4+(n-d=3n-S+3r2十”正确
2
对于B,因为4=2,6=2b,所以=2,所以数列{b,}是公比为2的等比数列,
b.
所以bn=bq-=2×2-=2”,所以Cn=46=3bn-1=32”-1,
所以Tn=3
21-2")
2-n=3.2*l-n-6,错误.
1-2
对于C,由B知Tn=3.2"-n-6,
所以T1-T=32m2-32m-1=32”-1>0恒成立,所以数列{亿}单调递增,
当n=8时,T=32°-8-6=1522<2025,
当n=9时,T,=320-9-6=3057>2025,
所以n的最大值为8,正确;
答案第4页,共8页
同课章节目录
