江苏无锡市湖滨中学2024-2025学年高一(下)数学第5周阶段性训练模拟练习(含解析)
文档属性
| 名称 | 江苏无锡市湖滨中学2024-2025学年高一(下)数学第5周阶段性训练模拟练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 18:37:39 | ||
图片预览

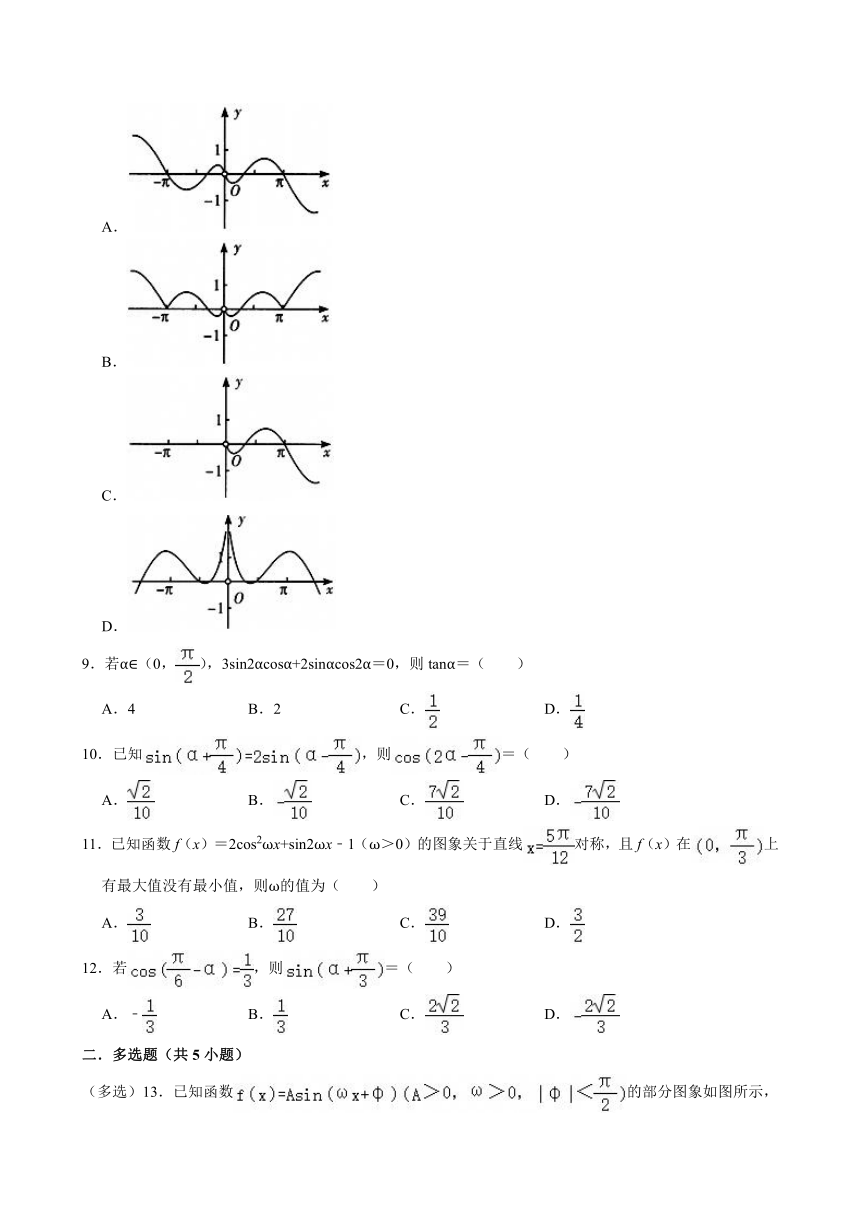



文档简介
高一数学下第一次月考真题打卡 (春季第5周)
一.选择题(共12小题)
1.已知函数的图象的一条对称轴为直线,且f(x1) f(x2)=﹣4,则|x1+x2|的最小值为( )
A. B.0 C. D.
2.已知,则=( )
A. B. C. D.
3.已知tanα=3,tan(α﹣β)=5,则=( )
A. B. C. D.5
4.=( )
A. B. C. D.
5.已知角α的终边经过点P(1,3),角β为钝角,且,则sinβ=( )
A. B. C. D.
6.将函数y=sin(x)的图象上所有点的横坐标缩短到原来的(纵坐标不变),得到的图象所对应的函数是( )
A.y=sin(x) B.y=sin(2x﹣)
C.y=sin() D.y=sin(2x)
7.设函数,若f(x)的图象经过点(0,1),且f(x)在[0,π]上恰有2个零点,则实数ω的取值范围是( )
A. B. C. D.
8.函数y=﹣cosxln|x|的图象可能是( )
A.
B.
C.
D.
9.若α∈(0,),3sin2αcosα+2sinαcos2α=0,则tanα=( )
A.4 B.2 C. D.
10.已知,则=( )
A. B. C. D.
11.已知函数f(x)=2cos2ωx+sin2ωx﹣1(ω>0)的图象关于直线对称,且f(x)在上有最大值没有最小值,则ω的值为( )
A. B. C. D.
12.若,则=( )
A.﹣ B. C. D.
二.多选题(共5小题)
(多选)13.已知函数的部分图象如图所示,则下列说法中正确的有( )
A.
B.直线是f(x)图象的一条对称轴
C.f(x)的图象可由函数y=2sinx的图象向左平移个单位长度,再将横坐标变为原来的倍(纵坐标不变)得到
D.若f(x1)=f(x2),则x1=x2+kπ(k∈Z)
(多选)14.已知函数,则下列说法中正确的有( )
A.f(x)的图象关于直线对称
B.f(x)的图象关于点对称
C.若f(x1)﹣f(x2)=2,则|x1﹣x2|的最小值为
D.若f(x1)+f(x2)=2(x1≠x2),则|x1+x2|的最小值为
(多选)15.已知函数f(x)=sinωx(ω>0),则下列说法正确的有( )
A.若f(x)在[0,π]上的值域为[﹣1,1],则ω的取值范围是
B.若f(x)在上恰有一条对称轴,则ω的取值范围是
C.若f(x)在上单调递增,则ω的取值范围是
D.若f(x)在上有且只有两个不同的零点,则ω的取值范围是(4,6]
(多选)16.用“五点法”画函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象时,列表并填入的部分数据如下表,则下列说法正确的是( )
x
ωx+φ 0 π 2π
Asin(ωx+φ) 0 2 0 ﹣2 0
A.A=2
B.不等式f(x)≥1的解集为
C.函数f(x)的图象关于直线对称
D.函数f(x)在区间上单调递增
(多选)17.已知函数f(x)=sin(sinx)﹣cos(cosx),则下列说法正确的是( )
A.f(x)是偶函数
B.f(x)是周期函数
C.f(x)关于直线对称
D.当x∈(0,π)时,﹣1<f(x)<0
三.解答题(共2小题)
18.如图,在直角坐标系xOy中,点P是单位圆上的动点,过点P作x轴的垂线,垂足为M,过O作射线交MP的延长线于点Q,使得S△OQM=2S△OPM,记∠MOP=α,∠QOM=β,且.
(1)若,求的值;
(2)已知函数f(α)=1﹣2m﹣2msinα﹣2cos2α,,记f(α)的最小值为g(m).若,求m的值及此时f(α)的最大值.
19.已知函数,其图象相邻两条对称轴之间的距离为,且经过点(0,1).
(1)求函数f(x)的解析式;
(2)当,方程有解,求实数m的取值范围;
(3)若方程f(x)﹣a=0在区间上恰有三个实数根x1,x2,x3,且x1<x2<x3,求sin(x1+x2+x3)的取值范围.
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10 11
答案 D A C D D D B D B B D
题号 12
答案 B
一.选择题(共12小题)
1.【解答】解:函数=sin(x+θ) 的图象的一条对称轴为直线,
∴f()=+=±,化简可得 (a﹣1)2=0,∴a=1.
∴f(x)=sinx﹣cosx=2sin(x﹣).
∵f(x1) f(x2)=﹣4,则f(x1)和f(x2)一个为﹣2,另一个为2,
不妨令 x1﹣=2kπ﹣,x2﹣=2kπ+,
即x1=2k1π﹣,x2=2k2π+,则|x1+x2|=|2(k1+k2)π+|,k1.k2∈Z.
故当k1+k2=0时,|x1+x2|取得最小值为.
故选:D.
2.【解答】解:设,
则,
,
则sinβ=,
故=sin(2β﹣﹣)=﹣cos2β=.
故选:A.
3.【解答】解:由于tanα=3,tan(α﹣β)=5,故,解得,
所以=.
故选:C.
4.【解答】解:原式=
=
=.
故选:D.
5.【解答】解:因为α的终边过点P(1,3),所以r=|OP|==,
所以sinα=,cosα=;
因为β为钝角,所以β∈(,π),
又因为α∈(2kπ,2kπ+),k∈Z,所以α+β∈(2kπ+,2kπ+),k∈Z;
又因为cos(α+β)=﹣,所以sin(α+β)=±=±;
当sin(α+β)=时,cosβ=cos[(α+β)﹣α]=cos(α+β)cosα+sin(α+β)sinα=﹣×+×=>0,不合题意,舍去;
所以sin(α+β)=﹣,sinβ=sin[(α+β)﹣α]=sin(α+β)cosα﹣cos(α+β)sinα=﹣×﹣(﹣)×=.
故选:D.
6.【解答】解:将函数y=sin(x)的图象上所有点的横坐标缩短到原来的(纵坐标不变),
就是ω变为原来的2倍进行变换,
即得到函数的解析式为:y=sin(2x).
故选:D.
7.【解答】解:由题意f(0)=1,可得,
又,
可得,
所以,
由x∈[0,π],可得,
由题意f(x)在[0,π]上恰有2个零点,
可得,
解得,即实数ω的取值范围是.
故选:B.
8.【解答】解:函数y=﹣cosxln|x|,满足f(﹣x)=f(x)所以函数是偶函数,所以排除AC,当x∈(0,1)时,函数y=﹣cosxln|x|>0,排除B,
故选:D.
9.【解答】解:因为3sin2αcosα+2sinαcos2α
=6sinαcos2α+2sinα(2cos2α﹣1)
=10sinαcos2α﹣2sinα=0,
又因为,所以sinα>0,
所以5cos2α﹣1=0,
所以,
所以tanα=2.
故选:B.
10.【解答】解:因为=﹣2cos(),
所以tan()=﹣2,
因为,所以tanα=3,
所以,,
即=(cos2α+sin2α)=()=﹣.
故选:B.
11.【解答】解:f(x)=2cos2ωx+sin2ωx﹣1=2 +sin2ωx﹣1=cos2ωx+sin2ωx=sin(2ωx+),x∈(0,),
所以2ωx+∈(,+),
因为f(x)在(0,)有最大值没有最小值,所以<+≤,解得<ω≤,
又因为f(x)的图象关于直线x=对称,所以+=+kπ,k∈Z,
解得ω=+,k∈Z,所以当k=1时,ω=符合要求.
故选:D.
12.【解答】解:∵,
∴=cos[﹣()]=cos(﹣α)=.
故选:B.
二.多选题(共5小题)
13.【解答】解:由f(x)的最大值为2,最小值为﹣2,可得A=2.
因为f(x)的周期T==π,所以,解得ω=2,
根据x=时,f(x)取得最大值为2,可得,k∈Z.
结合|φ|<,取k=0得φ=,所以f(x)=2sin(2x+).
对于A,由前面的分析可知φ=,所以A项正确;
对于B,当x=时,f()=2sin2π=0,不是最大值或最小值,
所以f(x)的图象不关于直线x=对称,故B项不正确;
对于C,函数y=2sinx的图象向左平移个单位长度,可得到y=2sin(x+)的图象,
然后将所得图象上点的横坐标变为原来的倍(纵坐标不变),
可得到y=2sin(2x+)的图象,即y=f(x)的图象,故C项正确;
对于D,若f(x1)=f(x2),则2x1+=2x2++2kπ或2x1+=π﹣(2x2+)+2kπ,k∈Z.
可得x1=x2+kπ或x1=﹣x2+kπ,k∈Z,故D项不正确.
故选:AC.
14.【解答】解:因为f()=sin≠±1,即函数图象不关于直线对称,A错误;
因为f()=sinπ=0,即函数的图象关于点对称,B正确;
若f(x1)﹣f(x2)=2,则f(x1)=1,f(x2)=﹣1,|x1﹣x2|的最小值为=,C正确;
若f(x1)+f(x2)=2,则f(x1)=1,f(x2)=1,|x1+x2|的最小值为﹣=,D错误.
故选:BC.
15.【解答】解:对于A,若f(x)在[0,π]上的值域为[﹣1,1],则,
所以T,即,
解得ω,即ω的取值范围是[,+∞),故A正确;
对于B,若f(x)在上恰有一条对称轴,则,
所以,
解得,即ω的取值范围是(,],故B错误;
对于C,若f(x)在上单调递增,则≥,
所以≥,
解得ω≤,即ω的取值范围是(0,],故C正确;
对于D,若f(x)在上有且只有两个不同的零点,则T<≤,
所以,
解得4<ω≤6,即ω的取值范围是(4,6],故D正确.
故选:ACD.
16.【解答】解:由题意得A=2,A正确;
因为==2π,
所以T=4π,,f(x)=2sin(φ),
又f()=2sin(φ﹣)=2且|φ|<π,
所以φ=,f(x)=2sin(),
令f(x)=2sin()≥1可得,k∈Z,
解得,,k∈Z,B错误;
f(﹣)=2sin=2为函数的最大值,即函数关于x=﹣对称,C正确;
令≤,k∈Z,
解得﹣,k∈Z,
当k=0时,一个单调递增区间为[﹣,﹣],
k=1时,一个单调递增区间为[,],D错误.
故选:AC.
17.【解答】解:,
,
则,
所以f(x)不是偶函数,故选项A错误;
f(x+2π)=sin(sin(x+2π))﹣cos(cos(x+2π))=sin(sinx)﹣cos(cosx)=f(x),
所以f(x)是以2π为周期的周期函数,故选项B正确;
f(π﹣x)=sin(sin(π﹣x))﹣cos(cos(π﹣x))=sin(sinx)﹣cos(cos(﹣x))=f(x),
所以f(x)关于直线对称,故选项C正确:
对于选项D,由f(x)关于直线对称,只需看当时,﹣1<f(x)<0是否成立即可.
当时,0<sinx≤1,0≤cosx<1,0<sin(sinx)≤sinl,cosl<cos(cosx)≤1,
所以sin(sinx)﹣cos(cosx)>﹣1,
又因为,
所以,
所以,
所以﹣1<f(x)<0,故选项D正确.
故选:BCD.
三.解答题(共2小题)
18.【解答】解:(1)因为sinα=,α∈(0,),所以cosα==,
由三角函数的定义可得P(cosα,sinα)=(,),
又S△OQM=2S△OPM,即|OM| |QM|=2×|OM||PM|,得|QM|=2|PM|,
所以Q(,),即|QM|=,所以|OQ|===,
所以sinβ==,cosβ==,
所以===﹣5;
(2)f(α)=1﹣2m﹣2msinα﹣2cos2α=1﹣2m﹣2msinα﹣2(1﹣sin2α)=2sin2α﹣2msinα﹣2m﹣1,
设t=sinα,α∈[,],则t∈[,],
所以原函数化为y=2t2﹣2mt﹣2m﹣1,对称轴为t=,
当≤,即m≤1时,g(m)=2×﹣m﹣2m﹣1=﹣3m﹣;
当<<,即1<m<时,g(m)=2×﹣2m ﹣2m﹣1=﹣m2﹣2m﹣1;
当≥,即m≥时,g(m)=2×﹣2m ﹣2m﹣1=﹣m﹣2m+,
综上,g(m)=,
因为g(m)=,
所以,解得m=﹣;
或,解得m=﹣1(舍)或m=﹣3(舍),
或,解得m=0(舍),
所以m=﹣,
此时y=2t2+t﹣,t∈[,],对称轴为t==﹣,
所以当t=时,ymax=2×+×﹣=,
即此时f(α)的最大值为.
19.【解答】解:(1)因为图象相邻两条对称轴之间的距离为,
所以=,
所以T=π,
即=π,所以ω=2,
所以,
又因为函数的图象过点(0,1),
所以2sinφ=1,sinφ=,
又因为|φ|<,
解得φ=,
所以f(x)=2sin(2x+);
(2)因为f(x﹣)=2sin[2(x﹣)+]=2sin(2x﹣)=﹣2cos2x,
当时,
所以2x∈[,],
所以cos2x∈[﹣1,],
所以f(x)=﹣2cos2x∈[﹣1,2],
所以方程有解,
即m=有解,
所以m∈[﹣1,2];
(3)作出函数y=f(x)在上的图象,如图所示:
因为方程f(x)﹣a=0在区间上恰有三个实数根x1,x2,x3,且x1<x2<x3,
即直线y=a与y=f(x)的图象在上恰有三个不同交点,
所以1≤a<2,
且x1与x2关于x=对称,
x2与x3关于x=对称,
所以x1+x2=,x2+x3=,
所以x1+x2+x3=﹣x2,
因为1≤a<2,
所以<x2≤,
所以﹣x2∈[,),
所以sin(x1+x2+x3)=sin(﹣x2)∈(﹣1,﹣].
一.选择题(共12小题)
1.已知函数的图象的一条对称轴为直线,且f(x1) f(x2)=﹣4,则|x1+x2|的最小值为( )
A. B.0 C. D.
2.已知,则=( )
A. B. C. D.
3.已知tanα=3,tan(α﹣β)=5,则=( )
A. B. C. D.5
4.=( )
A. B. C. D.
5.已知角α的终边经过点P(1,3),角β为钝角,且,则sinβ=( )
A. B. C. D.
6.将函数y=sin(x)的图象上所有点的横坐标缩短到原来的(纵坐标不变),得到的图象所对应的函数是( )
A.y=sin(x) B.y=sin(2x﹣)
C.y=sin() D.y=sin(2x)
7.设函数,若f(x)的图象经过点(0,1),且f(x)在[0,π]上恰有2个零点,则实数ω的取值范围是( )
A. B. C. D.
8.函数y=﹣cosxln|x|的图象可能是( )
A.
B.
C.
D.
9.若α∈(0,),3sin2αcosα+2sinαcos2α=0,则tanα=( )
A.4 B.2 C. D.
10.已知,则=( )
A. B. C. D.
11.已知函数f(x)=2cos2ωx+sin2ωx﹣1(ω>0)的图象关于直线对称,且f(x)在上有最大值没有最小值,则ω的值为( )
A. B. C. D.
12.若,则=( )
A.﹣ B. C. D.
二.多选题(共5小题)
(多选)13.已知函数的部分图象如图所示,则下列说法中正确的有( )
A.
B.直线是f(x)图象的一条对称轴
C.f(x)的图象可由函数y=2sinx的图象向左平移个单位长度,再将横坐标变为原来的倍(纵坐标不变)得到
D.若f(x1)=f(x2),则x1=x2+kπ(k∈Z)
(多选)14.已知函数,则下列说法中正确的有( )
A.f(x)的图象关于直线对称
B.f(x)的图象关于点对称
C.若f(x1)﹣f(x2)=2,则|x1﹣x2|的最小值为
D.若f(x1)+f(x2)=2(x1≠x2),则|x1+x2|的最小值为
(多选)15.已知函数f(x)=sinωx(ω>0),则下列说法正确的有( )
A.若f(x)在[0,π]上的值域为[﹣1,1],则ω的取值范围是
B.若f(x)在上恰有一条对称轴,则ω的取值范围是
C.若f(x)在上单调递增,则ω的取值范围是
D.若f(x)在上有且只有两个不同的零点,则ω的取值范围是(4,6]
(多选)16.用“五点法”画函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象时,列表并填入的部分数据如下表,则下列说法正确的是( )
x
ωx+φ 0 π 2π
Asin(ωx+φ) 0 2 0 ﹣2 0
A.A=2
B.不等式f(x)≥1的解集为
C.函数f(x)的图象关于直线对称
D.函数f(x)在区间上单调递增
(多选)17.已知函数f(x)=sin(sinx)﹣cos(cosx),则下列说法正确的是( )
A.f(x)是偶函数
B.f(x)是周期函数
C.f(x)关于直线对称
D.当x∈(0,π)时,﹣1<f(x)<0
三.解答题(共2小题)
18.如图,在直角坐标系xOy中,点P是单位圆上的动点,过点P作x轴的垂线,垂足为M,过O作射线交MP的延长线于点Q,使得S△OQM=2S△OPM,记∠MOP=α,∠QOM=β,且.
(1)若,求的值;
(2)已知函数f(α)=1﹣2m﹣2msinα﹣2cos2α,,记f(α)的最小值为g(m).若,求m的值及此时f(α)的最大值.
19.已知函数,其图象相邻两条对称轴之间的距离为,且经过点(0,1).
(1)求函数f(x)的解析式;
(2)当,方程有解,求实数m的取值范围;
(3)若方程f(x)﹣a=0在区间上恰有三个实数根x1,x2,x3,且x1<x2<x3,求sin(x1+x2+x3)的取值范围.
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10 11
答案 D A C D D D B D B B D
题号 12
答案 B
一.选择题(共12小题)
1.【解答】解:函数=sin(x+θ) 的图象的一条对称轴为直线,
∴f()=+=±,化简可得 (a﹣1)2=0,∴a=1.
∴f(x)=sinx﹣cosx=2sin(x﹣).
∵f(x1) f(x2)=﹣4,则f(x1)和f(x2)一个为﹣2,另一个为2,
不妨令 x1﹣=2kπ﹣,x2﹣=2kπ+,
即x1=2k1π﹣,x2=2k2π+,则|x1+x2|=|2(k1+k2)π+|,k1.k2∈Z.
故当k1+k2=0时,|x1+x2|取得最小值为.
故选:D.
2.【解答】解:设,
则,
,
则sinβ=,
故=sin(2β﹣﹣)=﹣cos2β=.
故选:A.
3.【解答】解:由于tanα=3,tan(α﹣β)=5,故,解得,
所以=.
故选:C.
4.【解答】解:原式=
=
=.
故选:D.
5.【解答】解:因为α的终边过点P(1,3),所以r=|OP|==,
所以sinα=,cosα=;
因为β为钝角,所以β∈(,π),
又因为α∈(2kπ,2kπ+),k∈Z,所以α+β∈(2kπ+,2kπ+),k∈Z;
又因为cos(α+β)=﹣,所以sin(α+β)=±=±;
当sin(α+β)=时,cosβ=cos[(α+β)﹣α]=cos(α+β)cosα+sin(α+β)sinα=﹣×+×=>0,不合题意,舍去;
所以sin(α+β)=﹣,sinβ=sin[(α+β)﹣α]=sin(α+β)cosα﹣cos(α+β)sinα=﹣×﹣(﹣)×=.
故选:D.
6.【解答】解:将函数y=sin(x)的图象上所有点的横坐标缩短到原来的(纵坐标不变),
就是ω变为原来的2倍进行变换,
即得到函数的解析式为:y=sin(2x).
故选:D.
7.【解答】解:由题意f(0)=1,可得,
又,
可得,
所以,
由x∈[0,π],可得,
由题意f(x)在[0,π]上恰有2个零点,
可得,
解得,即实数ω的取值范围是.
故选:B.
8.【解答】解:函数y=﹣cosxln|x|,满足f(﹣x)=f(x)所以函数是偶函数,所以排除AC,当x∈(0,1)时,函数y=﹣cosxln|x|>0,排除B,
故选:D.
9.【解答】解:因为3sin2αcosα+2sinαcos2α
=6sinαcos2α+2sinα(2cos2α﹣1)
=10sinαcos2α﹣2sinα=0,
又因为,所以sinα>0,
所以5cos2α﹣1=0,
所以,
所以tanα=2.
故选:B.
10.【解答】解:因为=﹣2cos(),
所以tan()=﹣2,
因为,所以tanα=3,
所以,,
即=(cos2α+sin2α)=()=﹣.
故选:B.
11.【解答】解:f(x)=2cos2ωx+sin2ωx﹣1=2 +sin2ωx﹣1=cos2ωx+sin2ωx=sin(2ωx+),x∈(0,),
所以2ωx+∈(,+),
因为f(x)在(0,)有最大值没有最小值,所以<+≤,解得<ω≤,
又因为f(x)的图象关于直线x=对称,所以+=+kπ,k∈Z,
解得ω=+,k∈Z,所以当k=1时,ω=符合要求.
故选:D.
12.【解答】解:∵,
∴=cos[﹣()]=cos(﹣α)=.
故选:B.
二.多选题(共5小题)
13.【解答】解:由f(x)的最大值为2,最小值为﹣2,可得A=2.
因为f(x)的周期T==π,所以,解得ω=2,
根据x=时,f(x)取得最大值为2,可得,k∈Z.
结合|φ|<,取k=0得φ=,所以f(x)=2sin(2x+).
对于A,由前面的分析可知φ=,所以A项正确;
对于B,当x=时,f()=2sin2π=0,不是最大值或最小值,
所以f(x)的图象不关于直线x=对称,故B项不正确;
对于C,函数y=2sinx的图象向左平移个单位长度,可得到y=2sin(x+)的图象,
然后将所得图象上点的横坐标变为原来的倍(纵坐标不变),
可得到y=2sin(2x+)的图象,即y=f(x)的图象,故C项正确;
对于D,若f(x1)=f(x2),则2x1+=2x2++2kπ或2x1+=π﹣(2x2+)+2kπ,k∈Z.
可得x1=x2+kπ或x1=﹣x2+kπ,k∈Z,故D项不正确.
故选:AC.
14.【解答】解:因为f()=sin≠±1,即函数图象不关于直线对称,A错误;
因为f()=sinπ=0,即函数的图象关于点对称,B正确;
若f(x1)﹣f(x2)=2,则f(x1)=1,f(x2)=﹣1,|x1﹣x2|的最小值为=,C正确;
若f(x1)+f(x2)=2,则f(x1)=1,f(x2)=1,|x1+x2|的最小值为﹣=,D错误.
故选:BC.
15.【解答】解:对于A,若f(x)在[0,π]上的值域为[﹣1,1],则,
所以T,即,
解得ω,即ω的取值范围是[,+∞),故A正确;
对于B,若f(x)在上恰有一条对称轴,则,
所以,
解得,即ω的取值范围是(,],故B错误;
对于C,若f(x)在上单调递增,则≥,
所以≥,
解得ω≤,即ω的取值范围是(0,],故C正确;
对于D,若f(x)在上有且只有两个不同的零点,则T<≤,
所以,
解得4<ω≤6,即ω的取值范围是(4,6],故D正确.
故选:ACD.
16.【解答】解:由题意得A=2,A正确;
因为==2π,
所以T=4π,,f(x)=2sin(φ),
又f()=2sin(φ﹣)=2且|φ|<π,
所以φ=,f(x)=2sin(),
令f(x)=2sin()≥1可得,k∈Z,
解得,,k∈Z,B错误;
f(﹣)=2sin=2为函数的最大值,即函数关于x=﹣对称,C正确;
令≤,k∈Z,
解得﹣,k∈Z,
当k=0时,一个单调递增区间为[﹣,﹣],
k=1时,一个单调递增区间为[,],D错误.
故选:AC.
17.【解答】解:,
,
则,
所以f(x)不是偶函数,故选项A错误;
f(x+2π)=sin(sin(x+2π))﹣cos(cos(x+2π))=sin(sinx)﹣cos(cosx)=f(x),
所以f(x)是以2π为周期的周期函数,故选项B正确;
f(π﹣x)=sin(sin(π﹣x))﹣cos(cos(π﹣x))=sin(sinx)﹣cos(cos(﹣x))=f(x),
所以f(x)关于直线对称,故选项C正确:
对于选项D,由f(x)关于直线对称,只需看当时,﹣1<f(x)<0是否成立即可.
当时,0<sinx≤1,0≤cosx<1,0<sin(sinx)≤sinl,cosl<cos(cosx)≤1,
所以sin(sinx)﹣cos(cosx)>﹣1,
又因为,
所以,
所以,
所以﹣1<f(x)<0,故选项D正确.
故选:BCD.
三.解答题(共2小题)
18.【解答】解:(1)因为sinα=,α∈(0,),所以cosα==,
由三角函数的定义可得P(cosα,sinα)=(,),
又S△OQM=2S△OPM,即|OM| |QM|=2×|OM||PM|,得|QM|=2|PM|,
所以Q(,),即|QM|=,所以|OQ|===,
所以sinβ==,cosβ==,
所以===﹣5;
(2)f(α)=1﹣2m﹣2msinα﹣2cos2α=1﹣2m﹣2msinα﹣2(1﹣sin2α)=2sin2α﹣2msinα﹣2m﹣1,
设t=sinα,α∈[,],则t∈[,],
所以原函数化为y=2t2﹣2mt﹣2m﹣1,对称轴为t=,
当≤,即m≤1时,g(m)=2×﹣m﹣2m﹣1=﹣3m﹣;
当<<,即1<m<时,g(m)=2×﹣2m ﹣2m﹣1=﹣m2﹣2m﹣1;
当≥,即m≥时,g(m)=2×﹣2m ﹣2m﹣1=﹣m﹣2m+,
综上,g(m)=,
因为g(m)=,
所以,解得m=﹣;
或,解得m=﹣1(舍)或m=﹣3(舍),
或,解得m=0(舍),
所以m=﹣,
此时y=2t2+t﹣,t∈[,],对称轴为t==﹣,
所以当t=时,ymax=2×+×﹣=,
即此时f(α)的最大值为.
19.【解答】解:(1)因为图象相邻两条对称轴之间的距离为,
所以=,
所以T=π,
即=π,所以ω=2,
所以,
又因为函数的图象过点(0,1),
所以2sinφ=1,sinφ=,
又因为|φ|<,
解得φ=,
所以f(x)=2sin(2x+);
(2)因为f(x﹣)=2sin[2(x﹣)+]=2sin(2x﹣)=﹣2cos2x,
当时,
所以2x∈[,],
所以cos2x∈[﹣1,],
所以f(x)=﹣2cos2x∈[﹣1,2],
所以方程有解,
即m=有解,
所以m∈[﹣1,2];
(3)作出函数y=f(x)在上的图象,如图所示:
因为方程f(x)﹣a=0在区间上恰有三个实数根x1,x2,x3,且x1<x2<x3,
即直线y=a与y=f(x)的图象在上恰有三个不同交点,
所以1≤a<2,
且x1与x2关于x=对称,
x2与x3关于x=对称,
所以x1+x2=,x2+x3=,
所以x1+x2+x3=﹣x2,
因为1≤a<2,
所以<x2≤,
所以﹣x2∈[,),
所以sin(x1+x2+x3)=sin(﹣x2)∈(﹣1,﹣].
同课章节目录
