8.1 不等式的基本性质 第2课时 课件 2024-2025学年青岛版八年级数学下册
文档属性
| 名称 | 8.1 不等式的基本性质 第2课时 课件 2024-2025学年青岛版八年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 18:38:56 | ||
图片预览





文档简介
(共13张PPT)
第八章 一元一次不等式
8.1 不等式的基本性质
第2课时
1.了解不等式的含义;
2.理解并掌握不等式的基本性质.
像a>b,-1<-4+ ,5x-2>2x+4这样,用“>”或“<”表示不等关系的式子叫做不等式.
新知生成
你还记得等式的基本性质吗?不等式有哪些基本性质呢?
等式的性质1:如果 a = b,那么 a + c = b + c,a – c = b – c;
等式的性质2:如果 a = b,那么 ac = bc , (c ≠ 0).
活动1:根据下列情境,回答相关问题,并猜想不等式具有哪些性质.
任务一:探究并掌握不等式的基本性质.
情境1:如图所示,托盘天平的右盘放上一质量为 b g 的铁球,左盘放上一质量为a g 的立体木块,天平向右倾斜.
问题:天平向右倾斜说明:质量上: a b;
若在两边同时加上一个 c g 的木块后:a + c b + c;
两边同时再将c g的木块拿掉后:a + c – c b + c – c.
a
b
a
b
c
c
+ c
c
– c
c
<
<
<
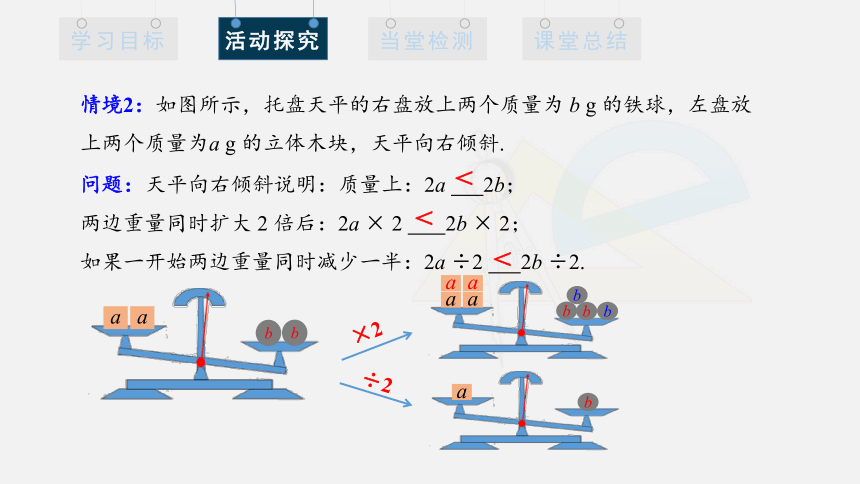
情境2:如图所示,托盘天平的右盘放上两个质量为 b g 的铁球,左盘放上两个质量为a g 的立体木块,天平向右倾斜.
问题:天平向右倾斜说明:质量上:2a 2b;
两边重量同时扩大 2 倍后:2a × 2 2b × 2;
如果一开始两边重量同时减少一半:2a ÷2 2b ÷2.
<
<
<
×2
a
b
a
b
a
b
a
a
a
b
b
b
÷2
a
b
活动小结
不等式基本性质1:不等式的两边都加上(或减去)同一个整式,
不等号方向不变.
如果a>b,那么a+c>b+c,a–c>b–c.
不等式基本性质2:不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
如果a>b,c>0,那么 ac>bc, .
已知3<5
则3×2______5×2;
<
<
3× ______5× ;
3÷2______5÷2;
3÷ ______5÷ ;
3÷ (-2)______5÷ (-2);
>
3÷ ______5÷ .
3×(-2)______5×(-2);
>
3× ______5× ;
>
>
活动2:仿照不等式的基本性质2,在不等式的两边都乘(或除以)同一个负数,看结果有何特点.
<
<
由此你发现了什么结论?
活动小结
不等式基本性质3:不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
如果a>b,c< 0,那么ac<bc,
事实上,如果a>b,c<0,
∵ac-bc=c(a–b)<0,∴ac<bc.
练一练
已知a<b,用“>”或“<”填空,并说明理由:
(1)a+2 b+2;
(2)a-3 b-3;
(3)a÷6 b÷6;
(4) -2a -2b.
<
<
<
>
思考:请根据 > 2,利用不等式的性质推出 < 2.5 .
解:∵ > 2,不等式两边同乘正数 ,
得( )2>2 (不等式的基本性质2),即5>2 .
∴ <2.5 .
不等式两边同除以2,得 (不等式的基本性质2),
1.已知a>b,若c是任意实数,则下列不等式中总是成立的是( )
A.a-c>b-c B.a+c<b+c
C.ac>bc D.ac<bc
2.用适当的不等号填空:
(1)若 a-1<b-1,则 a b;
(2)若 -3a<-3b,则 a b;
(3)若 0.3a+1<0.3b+1,则 a b;
(4)若 a>b,c<d,则a+d b+c.
A
<
>
<
>
<
3.已知a > b,用“>”或“<”填空:
(1)2a 2b ;
(2)-3a -3b ;
>
<
(3) .
针对本课关键词“不等式的性质”,说说你学到了什么?
性质1:如果a>b,那么a±c>b±c
不等式的性质
性质2:如果a>b,c>0,那么ac>bc(或 )
性质3:如果a>b,c<0,那么ac<bc(或 )
第八章 一元一次不等式
8.1 不等式的基本性质
第2课时
1.了解不等式的含义;
2.理解并掌握不等式的基本性质.
像a>b,-1<-4+ ,5x-2>2x+4这样,用“>”或“<”表示不等关系的式子叫做不等式.
新知生成
你还记得等式的基本性质吗?不等式有哪些基本性质呢?
等式的性质1:如果 a = b,那么 a + c = b + c,a – c = b – c;
等式的性质2:如果 a = b,那么 ac = bc , (c ≠ 0).
活动1:根据下列情境,回答相关问题,并猜想不等式具有哪些性质.
任务一:探究并掌握不等式的基本性质.
情境1:如图所示,托盘天平的右盘放上一质量为 b g 的铁球,左盘放上一质量为a g 的立体木块,天平向右倾斜.
问题:天平向右倾斜说明:质量上: a b;
若在两边同时加上一个 c g 的木块后:a + c b + c;
两边同时再将c g的木块拿掉后:a + c – c b + c – c.
a
b
a
b
c
c
+ c
c
– c
c
<
<
<
情境2:如图所示,托盘天平的右盘放上两个质量为 b g 的铁球,左盘放上两个质量为a g 的立体木块,天平向右倾斜.
问题:天平向右倾斜说明:质量上:2a 2b;
两边重量同时扩大 2 倍后:2a × 2 2b × 2;
如果一开始两边重量同时减少一半:2a ÷2 2b ÷2.
<
<
<
×2
a
b
a
b
a
b
a
a
a
b
b
b
÷2
a
b
活动小结
不等式基本性质1:不等式的两边都加上(或减去)同一个整式,
不等号方向不变.
如果a>b,那么a+c>b+c,a–c>b–c.
不等式基本性质2:不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
如果a>b,c>0,那么 ac>bc, .
已知3<5
则3×2______5×2;
<
<
3× ______5× ;
3÷2______5÷2;
3÷ ______5÷ ;
3÷ (-2)______5÷ (-2);
>
3÷ ______5÷ .
3×(-2)______5×(-2);
>
3× ______5× ;
>
>
活动2:仿照不等式的基本性质2,在不等式的两边都乘(或除以)同一个负数,看结果有何特点.
<
<
由此你发现了什么结论?
活动小结
不等式基本性质3:不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
如果a>b,c< 0,那么ac<bc,
事实上,如果a>b,c<0,
∵ac-bc=c(a–b)<0,∴ac<bc.
练一练
已知a<b,用“>”或“<”填空,并说明理由:
(1)a+2 b+2;
(2)a-3 b-3;
(3)a÷6 b÷6;
(4) -2a -2b.
<
<
<
>
思考:请根据 > 2,利用不等式的性质推出 < 2.5 .
解:∵ > 2,不等式两边同乘正数 ,
得( )2>2 (不等式的基本性质2),即5>2 .
∴ <2.5 .
不等式两边同除以2,得 (不等式的基本性质2),
1.已知a>b,若c是任意实数,则下列不等式中总是成立的是( )
A.a-c>b-c B.a+c<b+c
C.ac>bc D.ac<bc
2.用适当的不等号填空:
(1)若 a-1<b-1,则 a b;
(2)若 -3a<-3b,则 a b;
(3)若 0.3a+1<0.3b+1,则 a b;
(4)若 a>b,c<d,则a+d b+c.
A
<
>
<
>
<
3.已知a > b,用“>”或“<”填空:
(1)2a 2b ;
(2)-3a -3b ;
>
<
(3) .
针对本课关键词“不等式的性质”,说说你学到了什么?
性质1:如果a>b,那么a±c>b±c
不等式的性质
性质2:如果a>b,c>0,那么ac>bc(或 )
性质3:如果a>b,c<0,那么ac<bc(或 )
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
