人教版2024—2025学年八年级下册数学期末考试模拟试卷A卷(含答案+答题纸)
文档属性
| 名称 | 人教版2024—2025学年八年级下册数学期末考试模拟试卷A卷(含答案+答题纸) |

|
|
| 格式 | docx | ||
| 文件大小 | 380.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版2024—2025学年八年级下册数学期末考试模拟试卷A卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.在平面直角坐标系中,函数y=﹣x+1的图象经过( )象限.
A.第一、第二、第三 B.第二、第三、第四
C.第一、第三、第四 D.第一、第二、第四
2.下列各式中运算正确的是( )
A.22 B.
C. D.
3.下表记录了甲、乙、丙、丁四名跳高运动员最近10次训练成绩(单位:cm)的平均数与方差:
甲 乙 丙 丁
平均数 181 183 183 181
方差 1.6 3.4 1.6 3.4
要选择一名成绩好且发挥稳定的同学参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
4.下列命题正确的是( )
A.对角线相等的四边形是平行四边形
B.对角线相等且互相平分的四边形是菱形
C.对角线垂直且互相平分的四边形是矩形
D.对角线垂直、相等且互相平分的四边形是正方形
5.一个直角三角形的模具,量得其中两边长分别为4cm、3cm,则第三条边长为( )
A.5cm B.4cm C.cm D.5cm或cm
6.P1(x1,y1),P2(x2,y2)是一次函数y=2x﹣3图象上的两点,则下列判断正确的是( )
A.y1>y2 B.y1<y2
C.当x1<x2时,y1>y2 D.当x1<x2时,y1<y2
7.已知四边形ABCD是平行四边形,下列条件中,不能判定 ABCD为矩形的是( )
A.∠A=90° B.∠B=∠C C.AC=BD D.AC⊥BD
8.为了推进“阳光体育”,学校积极开展球类运动,在一次定点投篮测试中,每人投篮5次,七年级某班统计全班50名学生投中的次数,并记录如下:
投中次数(个) 0 1 2 3 4 5
人数(人) 1 ● 10 17 ● 6
表格中有两处数据不小心被墨汁遮盖了,下列关于投中次数的统计量中可以确定的是( )
A.平均数 B.中位数 C.众数 D.方差
9.当2≤x≤5时,一次函数y=(m+1)x+m2+1有最大值6,则实数m的值为( )
A.﹣3或0 B.0或1 C.﹣5或﹣3 D.﹣5或1
10.如图,在边长为6的正方形ABCD中,点E,F分别是边AB,BC上的动点,且满足AE=BF,AF与DE交于点O,点M是DF的中点,G是边AB上的点,AG=2GB,则OM+FG的最小值是( )
A.4 B.5
C.8 D.10
.二、填空题(6小题,每题3分,共18分)
11.比较大小:6 7.(填“>”,“=”,“<”号)
12. ABCD中,∠A+∠C=140°,则∠B= .
13.要使式子有意义,则a的取值范围是 .
14.实数a、b在数轴上位置如图,化简:|a+b|+= .
15.若一次函数y=(k+1)x+2k﹣4的图象不经过第二象限,则k的取值范围是 .
16.如图1,在菱形ABCD中,动点P从点C出发,沿C→A→D运动至终点D.设点P的运动路程为x,△BCP的面积为y,若y与x的函数图象如图2所示,则图中a的值为 .
第II卷
人教版2024—2025学年八年级下册数学期末考试模拟试卷A卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
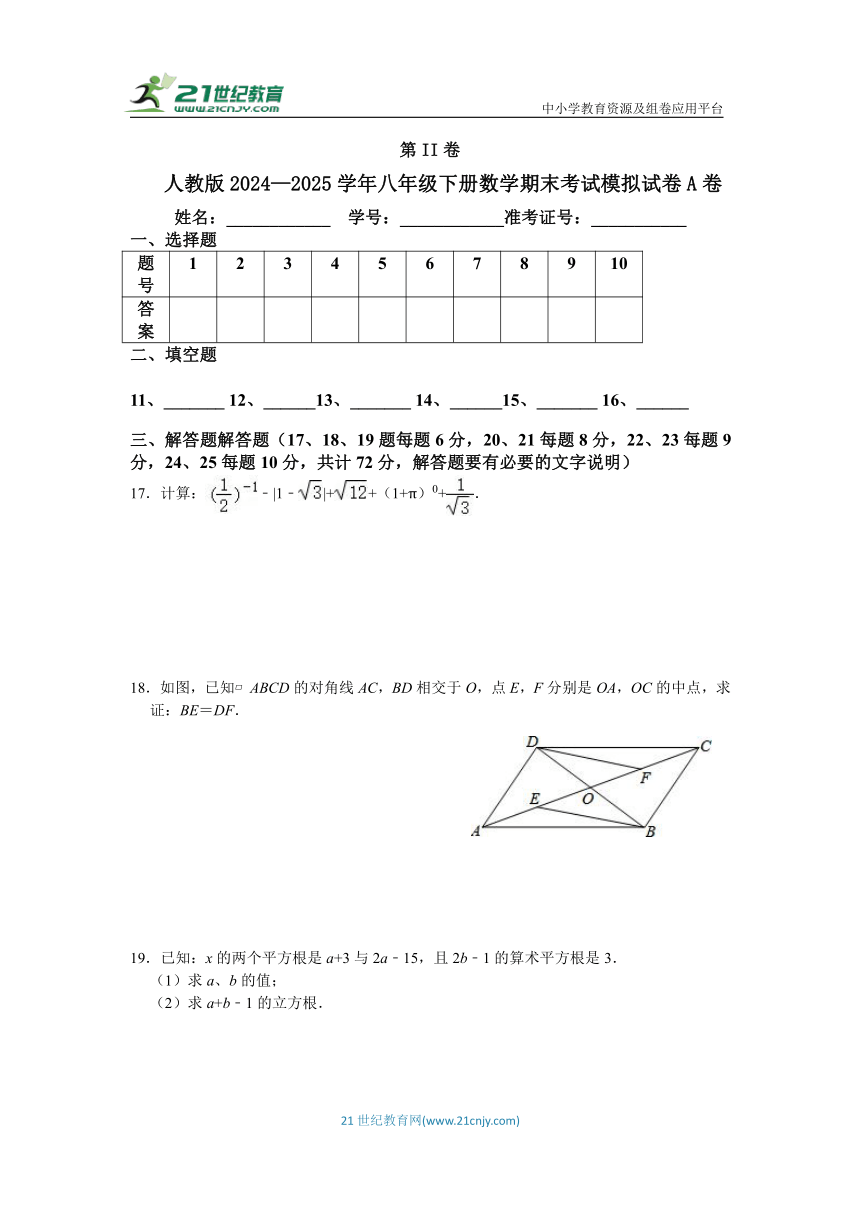
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:﹣|1﹣|++(1+π)0+.
18.如图,已知 ABCD的对角线AC,BD相交于O,点E,F分别是OA,OC的中点,求证:BE=DF.
19.已知:x的两个平方根是a+3与2a﹣15,且2b﹣1的算术平方根是3.
(1)求a、b的值;
(2)求a+b﹣1的立方根.
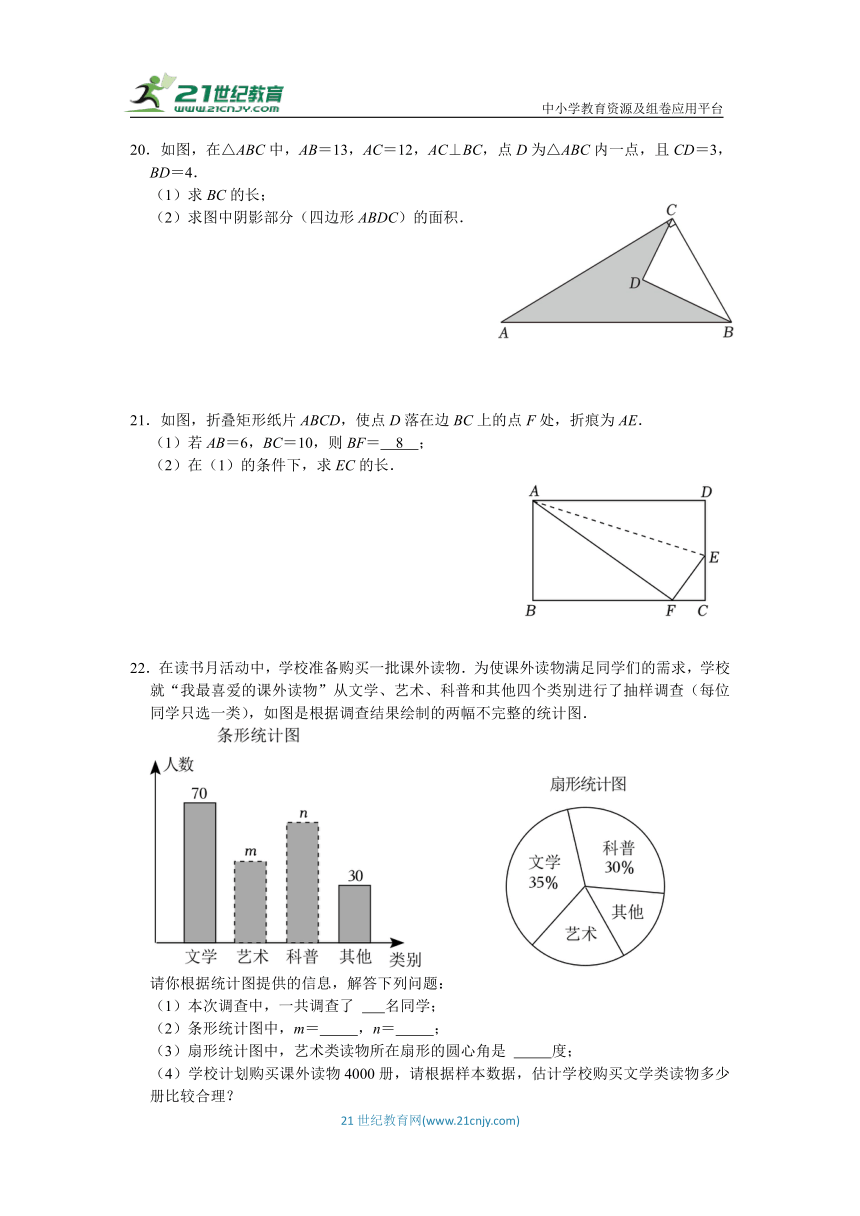
20.如图,在△ABC中,AB=13,AC=12,AC⊥BC,点D为△ABC内一点,且CD=3,BD=4.
(1)求BC的长;
(2)求图中阴影部分(四边形ABDC)的面积.
21.如图,折叠矩形纸片ABCD,使点D落在边BC上的点F处,折痕为AE.
(1)若AB=6,BC=10,则BF= 8 ;
(2)在(1)的条件下,求EC的长.
22.在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划购买课外读物4000册,请根据样本数据,估计学校购买文学类读物多少册比较合理?
23.当排球和足球纳入中招考试体育加试后,这两种球的销量逐步提升.某体育用品商店看准时机,第一次购入30个排球和70个足球共花费4550元.第二次购入60个排球和40个足球共花费4100元.商店将排球和足球以50元/个和70元/个的价格出售,前两次进货很快销售一空.
(1)求每个排球和足球的进价.
(2)该商店准备第三次购入排球和足球共200个,根据市场需求,排球的购买个数不少于40个且不超过100个.购买时生产厂家对排球进行了优惠,规定购买排球不超过50个时保持原价,超过50个时超过的部分打八折.设第三次进货销售完的总利润为W元(利润=销售额﹣成本),其中购进排球x个.
①求W与x的函数关系式.
②商店为了回馈顾客,开展促销活动.将其中的m(m为正整数)个排球按30元/个,3m个足球按50元/个进行销售.若第三次进货销售完后,获得的最大利润不能低于3000元,求m的最大值.
24.如图,矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上,线段OA、OC的长度满足|OA﹣15|+=0,点N在OC上,将△BCN沿直线BN折叠,点C恰好落在x轴上的点D处,且OD=3.
(1)求点B的坐标;
(2)求直线BN的解析式;
(3)坐标平面内是否存在一点P,使以B、N,D、P为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
25.如图,在平面直角坐标系中,菱形ABCD的四个顶点在坐标轴上,C,D两点的坐标分
别是(6,0),(0,2),BE⊥AD于E,F是BC的中点,点P(a,b)在直线BE上.
(1)求直线BE的解析式;
(2)当DP+FP的值最小时,求点P的坐标;
(3)当△DPF是等腰三角形,且ab>0时,写出点P的坐标.
参考答案
一、选择题
1.【解答】解:函数y=﹣x+1,
当x=0时,y=1,故函数经过(0,1)点,
当y=0时,x=1,故函数经过(1,0)点,
函数图象如下图:
由图可知函数经过第一、第二、第四象限.
故选:D.
2.【解答】解:A、22,故该项不正确,不符合题意;
B、2,故该项不正确,不符合题意;
C、,故该项正确,符合题意;
D、2,故该项不正确,不符合题意;
故选:C.
3.【解答】解:∵乙,丙的平均数较大,
∴从乙和丙中选择一人参加比赛,
∵S丙2<S乙2,
∴选择丙参赛,
故选:C.
4.【解答】解:对角线互相平分的四边形是平行四边形,故A错误,不符合题意;
对角线垂直且互相平分的四边形是菱形,故B错误,不符合题意;
对角线相等且互相平分的四边形是矩形,故C错误,不符合题意;
对角线垂直、相等且互相平分的四边形是正方形,故D正确,符合题意;
故选:D.
5.【解答】解:①当4是直角边时,斜边==5,此时第三边为5;
②当4为斜边时,此时第三边==
综上可得第三边的长度为5或.
故选:D.
6.【解答】解:∵k=2>0,
∴y随x的增大而增大,
∴当x1<x2时,y1<y2.
故选:D.
7.【解答】解:∵四边形ABCD是平行四边形,
∴当∠A=90°,平行四边形ABCD是矩形,
∴选项A可以判定 ABCD为矩形,
故选项A不符合题意;
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
当∠B=∠C时,则∠B=∠C=90°,此时 ABCD为矩形,
故选项B可以判定 ABCD为矩形,
故选项B不符合题意;
∵四边形ABCD是平行四边形,
当 AC=BD时,平行四边形ABCD是矩形,
∴选项C可以判定 ABCD为矩形,
故选项C不符合题意;
∵四边形ABCD是平行四边形,
当AC⊥BD时,平行四边形ABCD是菱形,
∴选项D不能判定 ABCD为矩形,
故选项D符合题意.
故选:D.
8.【解答】解:∵被墨汁遮盖的人数为50﹣1﹣10﹣17﹣6=16,
∴投中的3次的人数最多,是17,
∴投中次数的统计量中可以确定的是众数,
故选:C.
9.【解答】解:当m+1>0,即m>﹣1时,y随x的增大而增大,
∴当x=5时,一次函数y=(m+1)x+m2+1有最大值6,
∴5(m+1)+m2+1=6,
解得m1=0,m2=﹣5(舍去),
当m+1<0,即m<﹣1时,y随x的增大而减小,
∴当x=2时,一次函数y=(m+1)x+m2+1有最大值6,
∴2(m+1)+m2+1=6,
解得m1=﹣3,m2=1(舍去),
综上,当2≤x≤5时,一次函数y=(m+1)x+m2+1有最大值6,则实数m的值为0或﹣3,
故选:A.
10.【解答】解:∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠ABC=90°,
又∵AE=BF,
∴△ADE≌△BAF(SAS),
∴∠ADE=∠BAF,
∴∠DOF=∠ADO+∠DAO=∠BAF+∠DAO=∠DAB=90°,
∵点M是DF的中点,
∴,
如图所示,在AB延长线上截取BH=BG,连接FH,
∵FBG=∠FBH=90°,FB=FB,BG=BH,
∴△FBG≌△FBH(SAS),
∴FH=FG,
∴,
∴当H、D、F三点共线时,DF+HF有最小值,即此时有最小值,最小值即为DH的长的一半,
∵AG=2GB,AB=6,
∴BH=BG=2,
∴AH=8,
在Rt△ADH中,由勾股定理得.
∴的最小值为5,
故选:B.
二、填空题
11.【解答】解:6==,7==,
∵180>147,
∴6>7,
故答案为:>.
12.【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD∥BC,
∴∠A+∠B=180°,
∵∠A+∠C=140°,
∴∠A=70°,
∴∠B=180°﹣70°=110°,
故答案为:110°.
13.【解答】解:由题意得:a+1≥0,
解得:a≥﹣1,
故答案为:a≥﹣1.
14.【解答】解:由题意可知:a<0<b,
∴a+b<0,a﹣b<0,
∴原式=﹣(a+b)﹣(a﹣b)
=﹣a﹣b﹣a+b
=﹣2a,
故答案为:﹣2a
15.【解答】解:∵一次函数y=(k+1)x+2k﹣4的图象不经过第二象限,
∴k+1>0且2k﹣4≤0,
解得﹣1<k≤2,
∴k的取值范围是﹣1<k≤2.
故答案为:﹣1<k≤2.
16.【解答】解:如图1,连接BD交AC于点M,
由图2知,AC=12,且CP=12时,△BCP的面积为48,
∵四边形ABCD是菱形,
∴BD⊥AC,且AM=6,BM=MD,
∴,
∴BM=8,
∴DM=8,
∴AD=10,
∴a=CA+AD=12+10=22.
故答案为:22.
三、解答题
17.【解答】解:原式=
=
=
=.
18.【解答】证明:连接BF、DE,如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E、F分别是OA、OC的中点,
∴OE=OA,OF=OC,
∴OE=OF,
∴四边形BFDE是平行四边形,
∴BE∥DF.
19.【解答】解:(1)解:∵x的平方根是a+3与2a﹣15,且2b﹣1的算术平方根是3,
∴a+3+2a﹣15=0,2b﹣1=9,
解得:a=4,b=5;
(2)∵a=4,b=5,
∴a+b﹣1=4+5﹣1=8,
∴a+b﹣1的立方根是2.
20.【解答】解:(1)在Rt△ABC中,AC2+BC2=AB2,
∴;
(2)∵CD=3,BD=4,BC=5,
∴CD2+BD2=BC2,
∴△BCD为直角三角形,且∠BDC=90°,
∴.
∵,
∴S四边形ABDC=S△ABC﹣S△BCD=24.
21.【解答】解:(1)∵四边形ABCD是长方形,
∴AD=BC=10,CD=AB=6,
∵长方形纸片沿AE折叠,点D落在BC边的点F处,
∴AF=AD=10,EF=DE,
在Rt△ABF中,;
(2)由(1)知BF=8,
∴FC=BC﹣BF=10﹣8=2,
设DE=x,则EC=CD﹣DE=6﹣x,
在Rt△CEF中,EC2+FC2=EF2,
即(6﹣x)2+22=x2,
解得,
∴.
22.【解答】解:(1)根据条形图得出文学类人数为:70,利用扇形图得出文学类所占百分比为:35%,
故本次调查中,一共调查了:70÷35%=200(人),
故答案为:200;
(2)根据科普类所占百分比为:30%,
则科普类人数为:n=200×30%=60(人),
m=200﹣70﹣30﹣60=40(人),
故m=40,n=60;
故答案为:40,60;
(3)艺术类读物所在扇形的圆心角是:×360°=72°,
故答案为:72;
(4)由题意,得4000×=600(册).
23.【解答】解:(1)设排球的进价为每个a元,足球的进价为每个b元,
根据题意得:,
解方程组得:,
答:排球的进价为每个35元,足球的进价为每个50元;
(2)①当40≤x≤50时,W=(50﹣35)x+(70﹣50)(200﹣x)=﹣5x+4000,
当50<x≤100时,W=50x﹣[35×50+35×0.8×(x﹣50)]+(70﹣50)(200﹣x)=2x+3650;
∴W=;
②当40≤x≤50时,
根据题意得:W=(50﹣35)(x﹣m)+(30﹣35)m+(70﹣50)(200﹣x﹣3m)+(50﹣50)×3m=﹣5x+4000﹣80m,
∵﹣5<0,
∴W随x的增大而减小,
∴当x=40时,W的值最大,最大值为﹣80m+3800,
∴﹣80m+3800≥3000,
解不等式得:m≤10;
当50<x≤100时,W=[50(x﹣m)+30m]﹣[35×50+35×0.8(x﹣50)]+(70﹣50)(200﹣x﹣3m)+(50﹣50)×3m=2x+3650﹣80m,
∵2>0,
∴W随x的增大而增大,
∴当x=100时,W的值最大,最大值为3850﹣80m,
∴﹣80m+3850≥3000,
解不等式得:m≤10.625,
∵m是正整数,
∴m的最大值为10.
答:m的最大值为10.
24.【解答】解:(1)∵|OA﹣15|+=0,
∴OA=15,OC=9,
∴OA=BC=15,AB=OC=9,
∴B(15,9);
(2)由折叠可知,BD=BC=15,∠BCO=∠BDN=90°,CN=DN,
设CN=m,则DN=m,ON=9﹣m,
在Rt△ABD中,∠BAO=90°,
由勾股定理可知,AD=12,
∴OD=3,
在Rt△ODN中,由勾股定理可知,(9﹣m)2+32=m2,
解得m=5,
∴ON=4,
∴N(0,4),
设直线BN的解析式为:y=kx+b,
∴,
∴,
∴直线BN的解析式为:y=x+4.
(3)存在,理由如下:
由上可知,B(15,0),N(0,4),D(3,0),
若以点B、N,D、P为顶点的四边形是平行四边形,根据题意,需要分以下三种情况:
①当BD为平行四边形的对角线时,xB+xD=xP+xN,yB+yD=yP+yN,
解得xP=18,yP=5,
∴P(18,5).
②当ND为平行四边形的对角线时,xN+xD=xB+xP,yN+yD=yB+yP,
解得xP=﹣12,yP=﹣5,
∴P(﹣12,﹣5).
③当BN为平行四边形的对角线时,xB+xN=xP+xD,yB+yN=yP+yD,
解得xP=12,yP=13,
∴P(12,13).
综上,符合题意的点P的坐标为(18,5)或(﹣12,﹣5)或(12,13).
25.【解答】解:(1)∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AB=BC=CD=AD,
∵C(6,0),D(0,2),
∴A(﹣6,0),B(0,﹣),
∴BD=4,AD==4,
∴AD=AB=BD=BC=CD,
∴△ABD和△BCD都是等边三角形.
∵BE⊥AD于E,F是BC的中点,
∴点E是AD中点,DF⊥BC,
∴E(﹣3,),
设直线BE的解析式为y=kx+b,将E(﹣3,),B(0,﹣)代入得,
,解得,
∴直线BE的解析式为y=;
(2)如图1,连接AF,交BE于点P,
∵EB垂直平分AD,
∴PA=PD,
∴DP+FP=PA+FP,
∵A、P、F三点共线,
∴DP+FP=PA+FP=AF最短,
∵B(0,﹣),C(6,0),F是BC的中点,
∴F(3,﹣),
设直线AF的解析式为y=kx+b,将F(3,﹣),A(﹣6,0)代入得,
,解得,
∴直线AF的解析式为y=,
∴,解得,
∴P();
(3)在菱形ABCD中,AD∥BC,
∵BE⊥AD,DF⊥BC,
∴BE=DF==6,DE=BF=,
∵△DPF是等腰三角形,点P(a,b)在直线BE上.且ab>0,
∴点P在第三象限,
①当DP=PF时,
Rt△DEP≌Rt△FBP(HL)
∴EP=BP,即点P为BE中点,
又∵E(﹣3,),B(0,﹣),
∴P();
②当PD=FD=6时,
如图2,作PH⊥y轴于点H,
在Rt△PDE中,PD=6,DE=,
∴PE==,
∴BP=6﹣,
∵P在直线BE上,
∴b=﹣﹣2,
∴PH=﹣a,BH=b﹣(﹣2)=﹣a,
在Rt△PBH中,PH2+BH2=BP2,
即,a2+3a2=(6﹣2)2,
∴a=﹣(3﹣)=﹣3,b=﹣3,
∴P(﹣3,﹣3);
③当PF=FD时,
如图2,连接FM,
设BE交x轴于点M,
∵∠BOM=∠BED,∠OBM=∠EBD,
∴△BOM∽△BED,
∴,即,
解得BM=4,
∴FM==<6,
∴PF>FM,
即点P在第二象限,不合题意,舍去,
综上所述,当△DPF是等腰三角形,且ab>0时,P的坐标为()或().
21世纪教育网(www.21cnjy.com)
人教版2024—2025学年八年级下册数学期末考试模拟试卷A卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.在平面直角坐标系中,函数y=﹣x+1的图象经过( )象限.
A.第一、第二、第三 B.第二、第三、第四
C.第一、第三、第四 D.第一、第二、第四
2.下列各式中运算正确的是( )
A.22 B.
C. D.
3.下表记录了甲、乙、丙、丁四名跳高运动员最近10次训练成绩(单位:cm)的平均数与方差:
甲 乙 丙 丁
平均数 181 183 183 181
方差 1.6 3.4 1.6 3.4
要选择一名成绩好且发挥稳定的同学参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
4.下列命题正确的是( )
A.对角线相等的四边形是平行四边形
B.对角线相等且互相平分的四边形是菱形
C.对角线垂直且互相平分的四边形是矩形
D.对角线垂直、相等且互相平分的四边形是正方形
5.一个直角三角形的模具,量得其中两边长分别为4cm、3cm,则第三条边长为( )
A.5cm B.4cm C.cm D.5cm或cm
6.P1(x1,y1),P2(x2,y2)是一次函数y=2x﹣3图象上的两点,则下列判断正确的是( )
A.y1>y2 B.y1<y2
C.当x1<x2时,y1>y2 D.当x1<x2时,y1<y2
7.已知四边形ABCD是平行四边形,下列条件中,不能判定 ABCD为矩形的是( )
A.∠A=90° B.∠B=∠C C.AC=BD D.AC⊥BD
8.为了推进“阳光体育”,学校积极开展球类运动,在一次定点投篮测试中,每人投篮5次,七年级某班统计全班50名学生投中的次数,并记录如下:
投中次数(个) 0 1 2 3 4 5
人数(人) 1 ● 10 17 ● 6
表格中有两处数据不小心被墨汁遮盖了,下列关于投中次数的统计量中可以确定的是( )
A.平均数 B.中位数 C.众数 D.方差
9.当2≤x≤5时,一次函数y=(m+1)x+m2+1有最大值6,则实数m的值为( )
A.﹣3或0 B.0或1 C.﹣5或﹣3 D.﹣5或1
10.如图,在边长为6的正方形ABCD中,点E,F分别是边AB,BC上的动点,且满足AE=BF,AF与DE交于点O,点M是DF的中点,G是边AB上的点,AG=2GB,则OM+FG的最小值是( )
A.4 B.5
C.8 D.10
.二、填空题(6小题,每题3分,共18分)
11.比较大小:6 7.(填“>”,“=”,“<”号)
12. ABCD中,∠A+∠C=140°,则∠B= .
13.要使式子有意义,则a的取值范围是 .
14.实数a、b在数轴上位置如图,化简:|a+b|+= .
15.若一次函数y=(k+1)x+2k﹣4的图象不经过第二象限,则k的取值范围是 .
16.如图1,在菱形ABCD中,动点P从点C出发,沿C→A→D运动至终点D.设点P的运动路程为x,△BCP的面积为y,若y与x的函数图象如图2所示,则图中a的值为 .
第II卷
人教版2024—2025学年八年级下册数学期末考试模拟试卷A卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:﹣|1﹣|++(1+π)0+.
18.如图,已知 ABCD的对角线AC,BD相交于O,点E,F分别是OA,OC的中点,求证:BE=DF.
19.已知:x的两个平方根是a+3与2a﹣15,且2b﹣1的算术平方根是3.
(1)求a、b的值;
(2)求a+b﹣1的立方根.
20.如图,在△ABC中,AB=13,AC=12,AC⊥BC,点D为△ABC内一点,且CD=3,BD=4.
(1)求BC的长;
(2)求图中阴影部分(四边形ABDC)的面积.
21.如图,折叠矩形纸片ABCD,使点D落在边BC上的点F处,折痕为AE.
(1)若AB=6,BC=10,则BF= 8 ;
(2)在(1)的条件下,求EC的长.
22.在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划购买课外读物4000册,请根据样本数据,估计学校购买文学类读物多少册比较合理?
23.当排球和足球纳入中招考试体育加试后,这两种球的销量逐步提升.某体育用品商店看准时机,第一次购入30个排球和70个足球共花费4550元.第二次购入60个排球和40个足球共花费4100元.商店将排球和足球以50元/个和70元/个的价格出售,前两次进货很快销售一空.
(1)求每个排球和足球的进价.
(2)该商店准备第三次购入排球和足球共200个,根据市场需求,排球的购买个数不少于40个且不超过100个.购买时生产厂家对排球进行了优惠,规定购买排球不超过50个时保持原价,超过50个时超过的部分打八折.设第三次进货销售完的总利润为W元(利润=销售额﹣成本),其中购进排球x个.
①求W与x的函数关系式.
②商店为了回馈顾客,开展促销活动.将其中的m(m为正整数)个排球按30元/个,3m个足球按50元/个进行销售.若第三次进货销售完后,获得的最大利润不能低于3000元,求m的最大值.
24.如图,矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上,线段OA、OC的长度满足|OA﹣15|+=0,点N在OC上,将△BCN沿直线BN折叠,点C恰好落在x轴上的点D处,且OD=3.
(1)求点B的坐标;
(2)求直线BN的解析式;
(3)坐标平面内是否存在一点P,使以B、N,D、P为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
25.如图,在平面直角坐标系中,菱形ABCD的四个顶点在坐标轴上,C,D两点的坐标分
别是(6,0),(0,2),BE⊥AD于E,F是BC的中点,点P(a,b)在直线BE上.
(1)求直线BE的解析式;
(2)当DP+FP的值最小时,求点P的坐标;
(3)当△DPF是等腰三角形,且ab>0时,写出点P的坐标.
参考答案
一、选择题
1.【解答】解:函数y=﹣x+1,
当x=0时,y=1,故函数经过(0,1)点,
当y=0时,x=1,故函数经过(1,0)点,
函数图象如下图:
由图可知函数经过第一、第二、第四象限.
故选:D.
2.【解答】解:A、22,故该项不正确,不符合题意;
B、2,故该项不正确,不符合题意;
C、,故该项正确,符合题意;
D、2,故该项不正确,不符合题意;
故选:C.
3.【解答】解:∵乙,丙的平均数较大,
∴从乙和丙中选择一人参加比赛,
∵S丙2<S乙2,
∴选择丙参赛,
故选:C.
4.【解答】解:对角线互相平分的四边形是平行四边形,故A错误,不符合题意;
对角线垂直且互相平分的四边形是菱形,故B错误,不符合题意;
对角线相等且互相平分的四边形是矩形,故C错误,不符合题意;
对角线垂直、相等且互相平分的四边形是正方形,故D正确,符合题意;
故选:D.
5.【解答】解:①当4是直角边时,斜边==5,此时第三边为5;
②当4为斜边时,此时第三边==
综上可得第三边的长度为5或.
故选:D.
6.【解答】解:∵k=2>0,
∴y随x的增大而增大,
∴当x1<x2时,y1<y2.
故选:D.
7.【解答】解:∵四边形ABCD是平行四边形,
∴当∠A=90°,平行四边形ABCD是矩形,
∴选项A可以判定 ABCD为矩形,
故选项A不符合题意;
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
当∠B=∠C时,则∠B=∠C=90°,此时 ABCD为矩形,
故选项B可以判定 ABCD为矩形,
故选项B不符合题意;
∵四边形ABCD是平行四边形,
当 AC=BD时,平行四边形ABCD是矩形,
∴选项C可以判定 ABCD为矩形,
故选项C不符合题意;
∵四边形ABCD是平行四边形,
当AC⊥BD时,平行四边形ABCD是菱形,
∴选项D不能判定 ABCD为矩形,
故选项D符合题意.
故选:D.
8.【解答】解:∵被墨汁遮盖的人数为50﹣1﹣10﹣17﹣6=16,
∴投中的3次的人数最多,是17,
∴投中次数的统计量中可以确定的是众数,
故选:C.
9.【解答】解:当m+1>0,即m>﹣1时,y随x的增大而增大,
∴当x=5时,一次函数y=(m+1)x+m2+1有最大值6,
∴5(m+1)+m2+1=6,
解得m1=0,m2=﹣5(舍去),
当m+1<0,即m<﹣1时,y随x的增大而减小,
∴当x=2时,一次函数y=(m+1)x+m2+1有最大值6,
∴2(m+1)+m2+1=6,
解得m1=﹣3,m2=1(舍去),
综上,当2≤x≤5时,一次函数y=(m+1)x+m2+1有最大值6,则实数m的值为0或﹣3,
故选:A.
10.【解答】解:∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠ABC=90°,
又∵AE=BF,
∴△ADE≌△BAF(SAS),
∴∠ADE=∠BAF,
∴∠DOF=∠ADO+∠DAO=∠BAF+∠DAO=∠DAB=90°,
∵点M是DF的中点,
∴,
如图所示,在AB延长线上截取BH=BG,连接FH,
∵FBG=∠FBH=90°,FB=FB,BG=BH,
∴△FBG≌△FBH(SAS),
∴FH=FG,
∴,
∴当H、D、F三点共线时,DF+HF有最小值,即此时有最小值,最小值即为DH的长的一半,
∵AG=2GB,AB=6,
∴BH=BG=2,
∴AH=8,
在Rt△ADH中,由勾股定理得.
∴的最小值为5,
故选:B.
二、填空题
11.【解答】解:6==,7==,
∵180>147,
∴6>7,
故答案为:>.
12.【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD∥BC,
∴∠A+∠B=180°,
∵∠A+∠C=140°,
∴∠A=70°,
∴∠B=180°﹣70°=110°,
故答案为:110°.
13.【解答】解:由题意得:a+1≥0,
解得:a≥﹣1,
故答案为:a≥﹣1.
14.【解答】解:由题意可知:a<0<b,
∴a+b<0,a﹣b<0,
∴原式=﹣(a+b)﹣(a﹣b)
=﹣a﹣b﹣a+b
=﹣2a,
故答案为:﹣2a
15.【解答】解:∵一次函数y=(k+1)x+2k﹣4的图象不经过第二象限,
∴k+1>0且2k﹣4≤0,
解得﹣1<k≤2,
∴k的取值范围是﹣1<k≤2.
故答案为:﹣1<k≤2.
16.【解答】解:如图1,连接BD交AC于点M,
由图2知,AC=12,且CP=12时,△BCP的面积为48,
∵四边形ABCD是菱形,
∴BD⊥AC,且AM=6,BM=MD,
∴,
∴BM=8,
∴DM=8,
∴AD=10,
∴a=CA+AD=12+10=22.
故答案为:22.
三、解答题
17.【解答】解:原式=
=
=
=.
18.【解答】证明:连接BF、DE,如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E、F分别是OA、OC的中点,
∴OE=OA,OF=OC,
∴OE=OF,
∴四边形BFDE是平行四边形,
∴BE∥DF.
19.【解答】解:(1)解:∵x的平方根是a+3与2a﹣15,且2b﹣1的算术平方根是3,
∴a+3+2a﹣15=0,2b﹣1=9,
解得:a=4,b=5;
(2)∵a=4,b=5,
∴a+b﹣1=4+5﹣1=8,
∴a+b﹣1的立方根是2.
20.【解答】解:(1)在Rt△ABC中,AC2+BC2=AB2,
∴;
(2)∵CD=3,BD=4,BC=5,
∴CD2+BD2=BC2,
∴△BCD为直角三角形,且∠BDC=90°,
∴.
∵,
∴S四边形ABDC=S△ABC﹣S△BCD=24.
21.【解答】解:(1)∵四边形ABCD是长方形,
∴AD=BC=10,CD=AB=6,
∵长方形纸片沿AE折叠,点D落在BC边的点F处,
∴AF=AD=10,EF=DE,
在Rt△ABF中,;
(2)由(1)知BF=8,
∴FC=BC﹣BF=10﹣8=2,
设DE=x,则EC=CD﹣DE=6﹣x,
在Rt△CEF中,EC2+FC2=EF2,
即(6﹣x)2+22=x2,
解得,
∴.
22.【解答】解:(1)根据条形图得出文学类人数为:70,利用扇形图得出文学类所占百分比为:35%,
故本次调查中,一共调查了:70÷35%=200(人),
故答案为:200;
(2)根据科普类所占百分比为:30%,
则科普类人数为:n=200×30%=60(人),
m=200﹣70﹣30﹣60=40(人),
故m=40,n=60;
故答案为:40,60;
(3)艺术类读物所在扇形的圆心角是:×360°=72°,
故答案为:72;
(4)由题意,得4000×=600(册).
23.【解答】解:(1)设排球的进价为每个a元,足球的进价为每个b元,
根据题意得:,
解方程组得:,
答:排球的进价为每个35元,足球的进价为每个50元;
(2)①当40≤x≤50时,W=(50﹣35)x+(70﹣50)(200﹣x)=﹣5x+4000,
当50<x≤100时,W=50x﹣[35×50+35×0.8×(x﹣50)]+(70﹣50)(200﹣x)=2x+3650;
∴W=;
②当40≤x≤50时,
根据题意得:W=(50﹣35)(x﹣m)+(30﹣35)m+(70﹣50)(200﹣x﹣3m)+(50﹣50)×3m=﹣5x+4000﹣80m,
∵﹣5<0,
∴W随x的增大而减小,
∴当x=40时,W的值最大,最大值为﹣80m+3800,
∴﹣80m+3800≥3000,
解不等式得:m≤10;
当50<x≤100时,W=[50(x﹣m)+30m]﹣[35×50+35×0.8(x﹣50)]+(70﹣50)(200﹣x﹣3m)+(50﹣50)×3m=2x+3650﹣80m,
∵2>0,
∴W随x的增大而增大,
∴当x=100时,W的值最大,最大值为3850﹣80m,
∴﹣80m+3850≥3000,
解不等式得:m≤10.625,
∵m是正整数,
∴m的最大值为10.
答:m的最大值为10.
24.【解答】解:(1)∵|OA﹣15|+=0,
∴OA=15,OC=9,
∴OA=BC=15,AB=OC=9,
∴B(15,9);
(2)由折叠可知,BD=BC=15,∠BCO=∠BDN=90°,CN=DN,
设CN=m,则DN=m,ON=9﹣m,
在Rt△ABD中,∠BAO=90°,
由勾股定理可知,AD=12,
∴OD=3,
在Rt△ODN中,由勾股定理可知,(9﹣m)2+32=m2,
解得m=5,
∴ON=4,
∴N(0,4),
设直线BN的解析式为:y=kx+b,
∴,
∴,
∴直线BN的解析式为:y=x+4.
(3)存在,理由如下:
由上可知,B(15,0),N(0,4),D(3,0),
若以点B、N,D、P为顶点的四边形是平行四边形,根据题意,需要分以下三种情况:
①当BD为平行四边形的对角线时,xB+xD=xP+xN,yB+yD=yP+yN,
解得xP=18,yP=5,
∴P(18,5).
②当ND为平行四边形的对角线时,xN+xD=xB+xP,yN+yD=yB+yP,
解得xP=﹣12,yP=﹣5,
∴P(﹣12,﹣5).
③当BN为平行四边形的对角线时,xB+xN=xP+xD,yB+yN=yP+yD,
解得xP=12,yP=13,
∴P(12,13).
综上,符合题意的点P的坐标为(18,5)或(﹣12,﹣5)或(12,13).
25.【解答】解:(1)∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AB=BC=CD=AD,
∵C(6,0),D(0,2),
∴A(﹣6,0),B(0,﹣),
∴BD=4,AD==4,
∴AD=AB=BD=BC=CD,
∴△ABD和△BCD都是等边三角形.
∵BE⊥AD于E,F是BC的中点,
∴点E是AD中点,DF⊥BC,
∴E(﹣3,),
设直线BE的解析式为y=kx+b,将E(﹣3,),B(0,﹣)代入得,
,解得,
∴直线BE的解析式为y=;
(2)如图1,连接AF,交BE于点P,
∵EB垂直平分AD,
∴PA=PD,
∴DP+FP=PA+FP,
∵A、P、F三点共线,
∴DP+FP=PA+FP=AF最短,
∵B(0,﹣),C(6,0),F是BC的中点,
∴F(3,﹣),
设直线AF的解析式为y=kx+b,将F(3,﹣),A(﹣6,0)代入得,
,解得,
∴直线AF的解析式为y=,
∴,解得,
∴P();
(3)在菱形ABCD中,AD∥BC,
∵BE⊥AD,DF⊥BC,
∴BE=DF==6,DE=BF=,
∵△DPF是等腰三角形,点P(a,b)在直线BE上.且ab>0,
∴点P在第三象限,
①当DP=PF时,
Rt△DEP≌Rt△FBP(HL)
∴EP=BP,即点P为BE中点,
又∵E(﹣3,),B(0,﹣),
∴P();
②当PD=FD=6时,
如图2,作PH⊥y轴于点H,
在Rt△PDE中,PD=6,DE=,
∴PE==,
∴BP=6﹣,
∵P在直线BE上,
∴b=﹣﹣2,
∴PH=﹣a,BH=b﹣(﹣2)=﹣a,
在Rt△PBH中,PH2+BH2=BP2,
即,a2+3a2=(6﹣2)2,
∴a=﹣(3﹣)=﹣3,b=﹣3,
∴P(﹣3,﹣3);
③当PF=FD时,
如图2,连接FM,
设BE交x轴于点M,
∵∠BOM=∠BED,∠OBM=∠EBD,
∴△BOM∽△BED,
∴,即,
解得BM=4,
∴FM==<6,
∴PF>FM,
即点P在第二象限,不合题意,舍去,
综上所述,当△DPF是等腰三角形,且ab>0时,P的坐标为()或().
21世纪教育网(www.21cnjy.com)
同课章节目录
