6.1 平行四边形及其性质 第2课时 课件(共10张PPT) 2024-2025学年青岛版八年级数学下册
文档属性
| 名称 | 6.1 平行四边形及其性质 第2课时 课件(共10张PPT) 2024-2025学年青岛版八年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-02 07:54:09 | ||
图片预览



文档简介
(共10张PPT)
第6章 平行四边形
6.1 平行四边形及其性质 第2课时
1.理解平行四边形对角线互相平分的性质,并能运用其解答有关几何问题.
任务一:理解平行四边形对角线互相平分的性质
活动:根据定义画出一个平行四边形ABCD,连接对角线AC、BD,并设它们相交于点O,量一量OA、OC、OB、OD的长度,你发现这四条线段有什么关系
A
B
D
C
O
OA=OC,OB=OD
问题:用所学知识论证你的发现(写出已知、求证和证明过程).
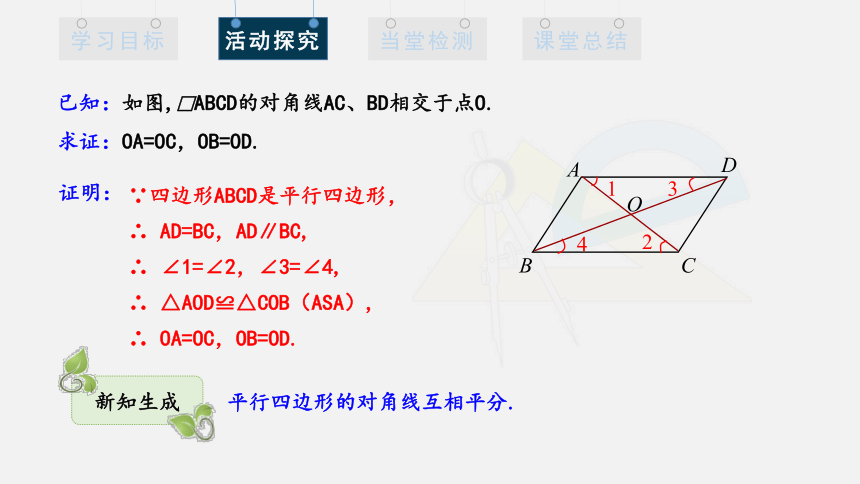
已知:如图,□ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC,
∴ ∠1=∠2,∠3=∠4,
∴ △AOD≌△COB(ASA),
∴ OA=OC,OB=OD.
A
C
D
B
O
3
2
4
1
新知生成
平行四边形的对角线互相平分.
活动:解决下列问题,并说说你的解题思路.
任务二:运用对角线互相平分的性质解答有关几何问题.
A
B
C
D
F
E
O
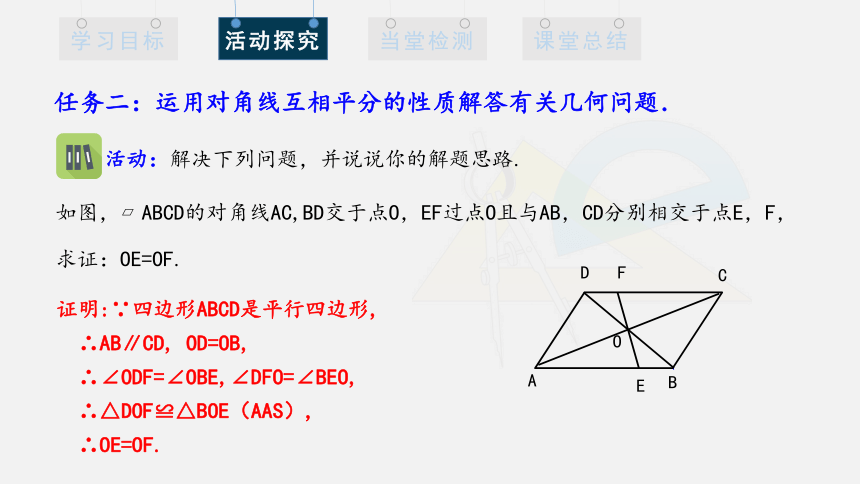
如图, ABCD的对角线AC,BD交于点O,EF过点O且与AB,CD分别相交于点E,F,求证:OE=OF.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD, OD=OB,
∴∠ODF=∠OBE,∠DFO=∠BEO,
∴△DOF≌△BOE(AAS),
∴OE=OF.
根据AD∥BC,OD=OB,易得△DOF≌△BOE(AAS)所以OE=OF的结论还会成立.
思考:如果前面问题中的条件“分别交 AB,CD 于点 E,F ”改为“分别交AD,BC的延长线于点F,E(如图)”,OE=OF还会成立吗?
A
B
C
D
F
E
O
练一练
如图,在平行四边形ABCD中,AC、BD交于O点,点E、F分别是AO、CO的中点.
求证:BE=DF且BE∥DF.
证明:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.
∵E,F分别是OA,OC的中点,∴OE=OF.
在△EOB和△FOD中
∵OE=OF,∠BOE=∠DOF,OB=OD
∴△EOB≌△FOD(SAS),∴BE=DF,∠FDB=∠EBD,
∴BE∥DF.
1.如图,平行四边形ABCD的对角线AC,BD交于点O,若AD=16,AC=24,BD=12,则△OBC的周长为( )
A.26 B.34 C.40 D.52
B
证明:如图,连接BD,交AC于点O.
∵四边形ABCD是平行四边形,四边形DEBF是平行四边形,
∴OA=OC,OE=OF,
∴OA-OE=OC-OF,
∴AE=CF.
2.如图, ABCD中,E、F在AC上,四边形DEBF是平行四边形.求证:AE=CF.
针对本节课的关键词“对角线”,你能说说学到了哪些知识吗?
平行四边形的性质
对角线互相平分
应用性质进行证明、计算
第6章 平行四边形
6.1 平行四边形及其性质 第2课时
1.理解平行四边形对角线互相平分的性质,并能运用其解答有关几何问题.
任务一:理解平行四边形对角线互相平分的性质
活动:根据定义画出一个平行四边形ABCD,连接对角线AC、BD,并设它们相交于点O,量一量OA、OC、OB、OD的长度,你发现这四条线段有什么关系
A
B
D
C
O
OA=OC,OB=OD
问题:用所学知识论证你的发现(写出已知、求证和证明过程).
已知:如图,□ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC,
∴ ∠1=∠2,∠3=∠4,
∴ △AOD≌△COB(ASA),
∴ OA=OC,OB=OD.
A
C
D
B
O
3
2
4
1
新知生成
平行四边形的对角线互相平分.
活动:解决下列问题,并说说你的解题思路.
任务二:运用对角线互相平分的性质解答有关几何问题.
A
B
C
D
F
E
O
如图, ABCD的对角线AC,BD交于点O,EF过点O且与AB,CD分别相交于点E,F,求证:OE=OF.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD, OD=OB,
∴∠ODF=∠OBE,∠DFO=∠BEO,
∴△DOF≌△BOE(AAS),
∴OE=OF.
根据AD∥BC,OD=OB,易得△DOF≌△BOE(AAS)所以OE=OF的结论还会成立.
思考:如果前面问题中的条件“分别交 AB,CD 于点 E,F ”改为“分别交AD,BC的延长线于点F,E(如图)”,OE=OF还会成立吗?
A
B
C
D
F
E
O
练一练
如图,在平行四边形ABCD中,AC、BD交于O点,点E、F分别是AO、CO的中点.
求证:BE=DF且BE∥DF.
证明:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.
∵E,F分别是OA,OC的中点,∴OE=OF.
在△EOB和△FOD中
∵OE=OF,∠BOE=∠DOF,OB=OD
∴△EOB≌△FOD(SAS),∴BE=DF,∠FDB=∠EBD,
∴BE∥DF.
1.如图,平行四边形ABCD的对角线AC,BD交于点O,若AD=16,AC=24,BD=12,则△OBC的周长为( )
A.26 B.34 C.40 D.52
B
证明:如图,连接BD,交AC于点O.
∵四边形ABCD是平行四边形,四边形DEBF是平行四边形,
∴OA=OC,OE=OF,
∴OA-OE=OC-OF,
∴AE=CF.
2.如图, ABCD中,E、F在AC上,四边形DEBF是平行四边形.求证:AE=CF.
针对本节课的关键词“对角线”,你能说说学到了哪些知识吗?
平行四边形的性质
对角线互相平分
应用性质进行证明、计算
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
