6.4 三角形的中位线定理 课件(共11张PPT) 2024-2025学年青岛版八年级数学下册
文档属性
| 名称 | 6.4 三角形的中位线定理 课件(共11张PPT) 2024-2025学年青岛版八年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-02 08:01:40 | ||
图片预览




文档简介
(共11张PPT)
第6章 平行四边形
6.4 三角形的中位线定理
1.理解三角形中位线的概念和定理.
2.运用三角形的中位线定理进行有关的证明和计算.
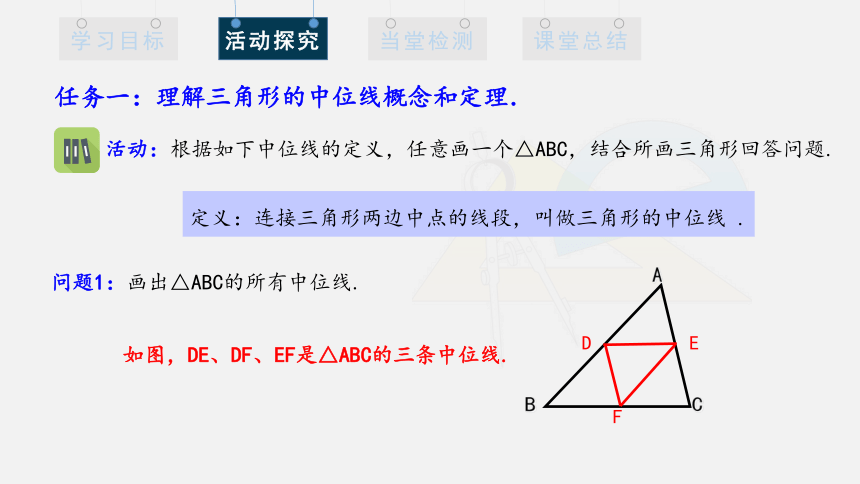
任务一:理解三角形的中位线概念和定理.
活动:根据如下中位线的定义,任意画一个△ABC,结合所画三角形回答问题.
问题1:画出△ABC的所有中位线.
定义:连接三角形两边中点的线段,叫做三角形的中位线 .
如图,DE、DF、EF是△ABC的三条中位线.
A
B
C
D
E
F
问题2:如图1,△ABC沿中位线DE剪开,得到的△ADE按图2方式拼接,点A与C重合,AE与CE重合,观察拼出的图形,小组合作解决下列问题.
(1)你发现拼出的图形是什么图形?说明你的理由.
(2)由拼出的图形,你发现中位线DE与底边BC有怎样的位置关系和数量关系?
(3)由(1)(2),写出三角形的中位线与第三边之间关系的猜想,并结合图形证明.
猜想:三角形的中位线平行于第三边且等于第三边的一半.
DE∥BC,DE= BC.
拼出的图形是平行四边形,
B C(A)
A
D
E
(D)
B C
A
D
E
图1
图2
猜想:三角形的中位线平行于第三边,并且等于第三边的一半.
已知:如图,在△ABC中,点D,E分别是AB,AC边的中点,
求证:DE∥BC,DE= BC
证明:
B C
A
D
E
延长DE至F,使EF=DE,连接CF,
∵AE=CE,∠AED=∠CEF,∴△ADE≌△CFE,
∴AD=CF,∠ADE=∠F,∴BD∥CF,
∵AD=BD,∴BD=CF,
∴四边形BCFD是平行四边形.
F
∴DF∥BC,DF=BC,
又∵ ∴
三角形的中位线定理:三角形的中位线平行于第三边且等于第三边的一半
任务二:应用三角形的中位线定理进行有关的证明和计算.
活动:请解决下列问题,简要归纳解题过程中用到的方法,谈谈你的收获.
已知:如图,在△ABC中,D,E,F分别是BC,AB,AC的中点.
求证:AD与EF互相平分.
连接DE,DF,
∵D,E,F分别是BC,AB,AC的中点.
∴DE,DF是△ABC的中位线.
∴DE∥AC,DF∥AB.
∴四边形AEDF为平行四边形.
∴AD与EF互相平分.
证明:
归纳:三角形的中位线定理的应用:常通过连接中点构造中位线解决平行四边形的判定,证明线段平行或等量倍分关系等问题.
练一练
如图,C、D分别为EA、EB的中点,∠E=30°,∠1=110°,求∠2的度数.
解:∵C、D分别为EA、EB的中点,
∴CD是△EAB的中位线,
∴CD ∥ AB,
∴∠2=∠ECD,
∵∠1=110°,∠E=30°,
∴∠ECD=80°,
∴∠2=80°.
1.如图,点D,E,F分别是△ABC的边AB,BC,CA的中点,以这些点为顶点,
能在图中画出 个平行四边形,若△ABC的周长为20,则以点D,E,F为
顶点的三角形的周长为 .
3
10
2.如图,四边形ABCD的对角线AC⊥BD,垂足为O,点E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是矩形.
证明:∵E、F、G、H分别是线段AB、BC、CD、AD的中点,
∴EF∥AC,GH∥AC且EF= AC,GH= AC,
∴四边形EFGH是平行四边形,
又∵AC⊥BD,
∴EF⊥FG,
∴四边形EFGH是矩形.
针对本课的以下关键词,你能说一说你都学到了哪些知识吗?
三角形的中位线
定义:连接三角形两边中点的线段
定理:三角形的中位线平行于三角形的
第三边,并且等于第三边的一半.
应用:判定平行四边形,证明线段
平行或等量倍分关系、求线段长等.
1.三角形中位线的概念和定理 2.三角形中位线定理的应用
第6章 平行四边形
6.4 三角形的中位线定理
1.理解三角形中位线的概念和定理.
2.运用三角形的中位线定理进行有关的证明和计算.
任务一:理解三角形的中位线概念和定理.
活动:根据如下中位线的定义,任意画一个△ABC,结合所画三角形回答问题.
问题1:画出△ABC的所有中位线.
定义:连接三角形两边中点的线段,叫做三角形的中位线 .
如图,DE、DF、EF是△ABC的三条中位线.
A
B
C
D
E
F
问题2:如图1,△ABC沿中位线DE剪开,得到的△ADE按图2方式拼接,点A与C重合,AE与CE重合,观察拼出的图形,小组合作解决下列问题.
(1)你发现拼出的图形是什么图形?说明你的理由.
(2)由拼出的图形,你发现中位线DE与底边BC有怎样的位置关系和数量关系?
(3)由(1)(2),写出三角形的中位线与第三边之间关系的猜想,并结合图形证明.
猜想:三角形的中位线平行于第三边且等于第三边的一半.
DE∥BC,DE= BC.
拼出的图形是平行四边形,
B C(A)
A
D
E
(D)
B C
A
D
E
图1
图2
猜想:三角形的中位线平行于第三边,并且等于第三边的一半.
已知:如图,在△ABC中,点D,E分别是AB,AC边的中点,
求证:DE∥BC,DE= BC
证明:
B C
A
D
E
延长DE至F,使EF=DE,连接CF,
∵AE=CE,∠AED=∠CEF,∴△ADE≌△CFE,
∴AD=CF,∠ADE=∠F,∴BD∥CF,
∵AD=BD,∴BD=CF,
∴四边形BCFD是平行四边形.
F
∴DF∥BC,DF=BC,
又∵ ∴
三角形的中位线定理:三角形的中位线平行于第三边且等于第三边的一半
任务二:应用三角形的中位线定理进行有关的证明和计算.
活动:请解决下列问题,简要归纳解题过程中用到的方法,谈谈你的收获.
已知:如图,在△ABC中,D,E,F分别是BC,AB,AC的中点.
求证:AD与EF互相平分.
连接DE,DF,
∵D,E,F分别是BC,AB,AC的中点.
∴DE,DF是△ABC的中位线.
∴DE∥AC,DF∥AB.
∴四边形AEDF为平行四边形.
∴AD与EF互相平分.
证明:
归纳:三角形的中位线定理的应用:常通过连接中点构造中位线解决平行四边形的判定,证明线段平行或等量倍分关系等问题.
练一练
如图,C、D分别为EA、EB的中点,∠E=30°,∠1=110°,求∠2的度数.
解:∵C、D分别为EA、EB的中点,
∴CD是△EAB的中位线,
∴CD ∥ AB,
∴∠2=∠ECD,
∵∠1=110°,∠E=30°,
∴∠ECD=80°,
∴∠2=80°.
1.如图,点D,E,F分别是△ABC的边AB,BC,CA的中点,以这些点为顶点,
能在图中画出 个平行四边形,若△ABC的周长为20,则以点D,E,F为
顶点的三角形的周长为 .
3
10
2.如图,四边形ABCD的对角线AC⊥BD,垂足为O,点E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是矩形.
证明:∵E、F、G、H分别是线段AB、BC、CD、AD的中点,
∴EF∥AC,GH∥AC且EF= AC,GH= AC,
∴四边形EFGH是平行四边形,
又∵AC⊥BD,
∴EF⊥FG,
∴四边形EFGH是矩形.
针对本课的以下关键词,你能说一说你都学到了哪些知识吗?
三角形的中位线
定义:连接三角形两边中点的线段
定理:三角形的中位线平行于三角形的
第三边,并且等于第三边的一半.
应用:判定平行四边形,证明线段
平行或等量倍分关系、求线段长等.
1.三角形中位线的概念和定理 2.三角形中位线定理的应用
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
