第九章统计同步练习卷(含解析)-2024-2025学年高一数学下学期人教A版(2019)必修第二册
文档属性
| 名称 | 第九章统计同步练习卷(含解析)-2024-2025学年高一数学下学期人教A版(2019)必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 758.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-03 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第九章统计同步练习卷-2024-2025学年高一数学下学期人教A版(2019)必修第二册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某政府机关在编人员共100人,其中副处级以上干部10人,一般干部70人,工人20人,上级部门为了了解该机关对政府机构改革的意见,要从中抽取20人,用下列哪种方法最合适( )
A.系统抽样法 B.简单随机抽样法
C.分层随机抽样法 D.随机数法
2.10名工人某天生产同一零件,生产的件数是15、17、14、10、15、17、17、16、14、12,设其平均数为,中位数为,众数为,则有( )
A. B. C. D.
3.为实现乡村生态振兴,走乡村绿色发展之路,某乡政府采用分层抽样的方式从甲村和乙村抽取部分村民参与环保调研,已知甲村和乙村的人数之比是10:9,被抽到的参与环保调研的村民中,甲村比乙村多7人,则参加调研的总人数是( )
A.133 B.170 C.70 D.63
4.为了了解某班学生数学成绩,利用分层随机抽样抽取了一个10人的样本,统计如下表:则可估计全班学生数学的平均分和方差分别为( )
学生数 平均分 方差
男生 6 80 4
女生 4 75 2
A.77.5,9.2 B.77.5,11 C.78,9.2 D.78,11
5.高二年级进行消防知识竞赛,统计所有参赛同学的成绩,成绩都在内,估计所有参赛同学成绩的第75百分位数为( )
A. B. C. D.
6.已知总体划分为3层,按比例用分层随机抽样法抽样,各层的样本量及样本平均数如下表:
分层 样本量 样本平均数
第一层 10 55
第二层 30 75
第三层 10 90
估计总体平均数为( )
A.73 B.74 C.76 D.80
7.已知某人收集一个样本容量为50的一组数据,并求得其平均数为70,方差为75,现发现在收集这些数据时,其中得两个数据记录有误,一个错将80记录为60,另一个错将70记录为90,在对错误的数据进行更正后,重新求得样本的平均数为,方差为,则( )
A. B.
C. D.
8.某校组织50名学生参加庆祝中华人民共和国成立75周年知识竞赛,经统计这50名学生的成绩都在区间内,按分数分成5组:,,,,,得到如图所示的频率分布直方图(不完整),根据图中数据,下列结论错误的是( )
A.成绩在上的人数最多
B.成绩不低于70分的学生所占比例为
C.50名学生成绩的平均分小于中位数
D.50名学生成绩的极差为50
二、多选题
9.已知样本数据90,100,95,110,105,则( )
A.极差为20 B.平均数为103 C.方差为50 D.分位数为97
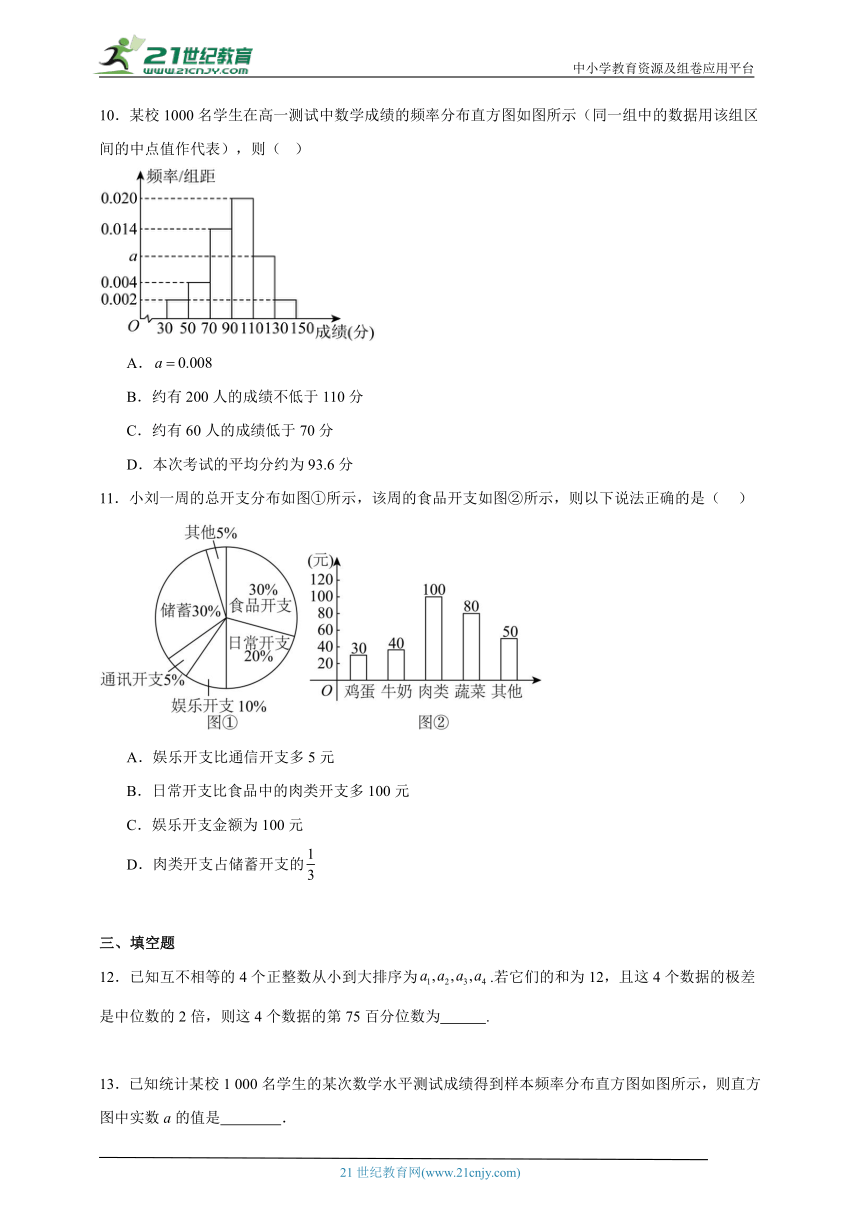
10.某校1000名学生在高一测试中数学成绩的频率分布直方图如图所示(同一组中的数据用该组区间的中点值作代表),则( )
A.
B.约有200人的成绩不低于110分
C.约有60人的成绩低于70分
D.本次考试的平均分约为93.6分
11.小刘一周的总开支分布如图①所示,该周的食品开支如图②所示,则以下说法正确的是( )
A.娱乐开支比通信开支多5元
B.日常开支比食品中的肉类开支多100元
C.娱乐开支金额为100元
D.肉类开支占储蓄开支的
三、填空题
12.已知互不相等的4个正整数从小到大排序为.若它们的和为12,且这4个数据的极差是中位数的2倍,则这4个数据的第75百分位数为 .
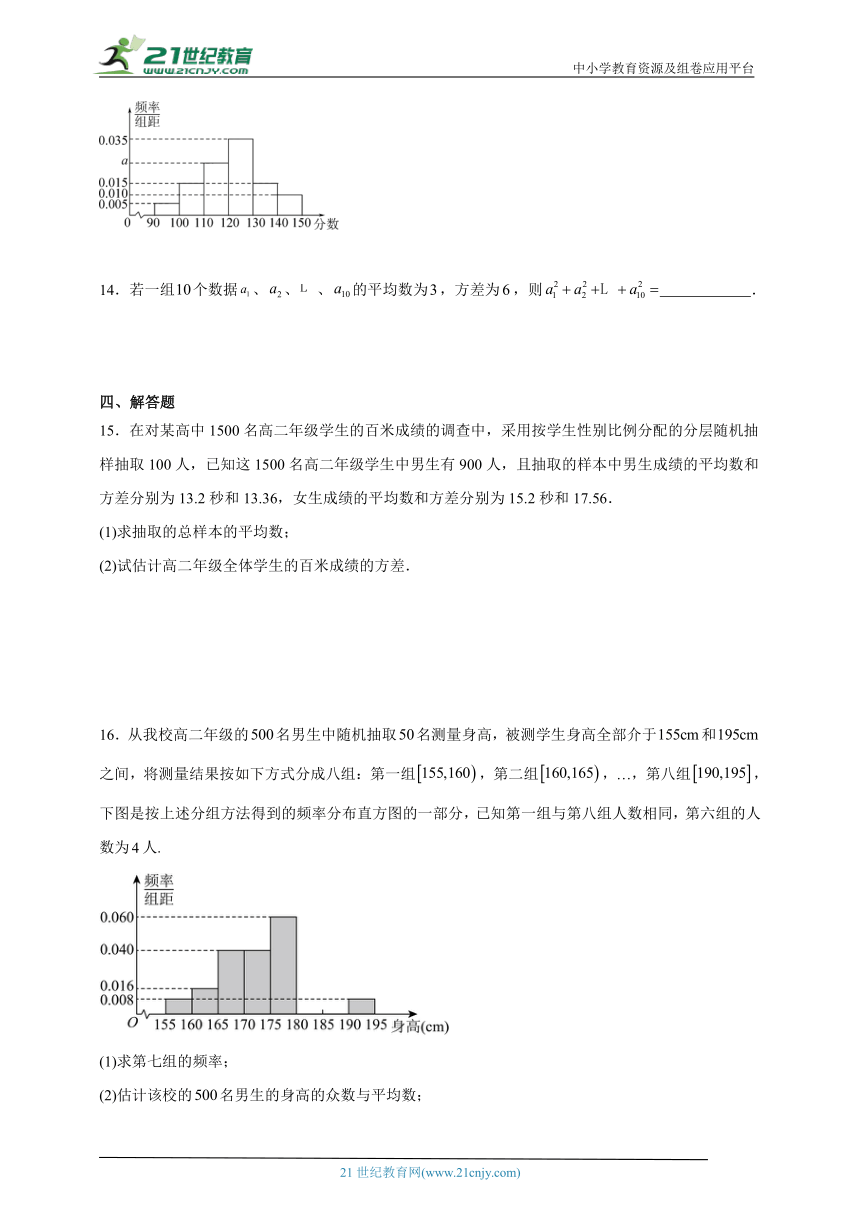
13.已知统计某校1 000名学生的某次数学水平测试成绩得到样本频率分布直方图如图所示,则直方图中实数a的值是 .
14.若一组个数据、、、的平均数为,方差为,则 .
四、解答题
15.在对某高中1500名高二年级学生的百米成绩的调查中,采用按学生性别比例分配的分层随机抽样抽取100人,已知这1500名高二年级学生中男生有900人,且抽取的样本中男生成绩的平均数和方差分别为13.2秒和13.36,女生成绩的平均数和方差分别为15.2秒和17.56.
(1)求抽取的总样本的平均数;
(2)试估计高二年级全体学生的百米成绩的方差.
16.从我校高二年级的名男生中随机抽取名测量身高,被测学生身高全部介于和之间,将测量结果按如下方式分成八组:第一组,第二组,…,第八组,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为人.
(1)求第七组的频率;
(2)估计该校的名男生的身高的众数与平均数;
17.有900名学生参加“环保知识竞赛”,为考察竞赛成绩情况,从中抽取部分学生的成绩(得分均整数,满分为100分)进行统计,请你根据尚未完成并有局部污损的频率分面表和频率分布直方图(如图)解释下列问题.
分组 频数 频率
4 0.08
0.16
10
16 0.32
合计 50
(1)填满频率分布表;
(2)补全频率分布直方图;
(3)若成绩在的学生可以获得二等奖,求获得二等奖的学生人数.
18.有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:
甲:7 8 7 9 5 4 9 10 7 4
乙:9 5 7 8 7 6 8 6 7 7
设甲、乙两名运动员射击平均环数分别记为和,方差分别记为和.
(1)求,,,;
(2)如果你是教练,你如何对这次射击情况作出评价?如果这是一次选拔性考核,你应当如何作出选择?
19.已知某科技公司的某型号芯片的各项指标经过全面检测后,分为I级和Ⅱ级,两种品级芯片的某项指标的频率分布直方图如图所示:
若只利用该指标制定一个标准,需要确定临界值K,将该指标大于K的产品应用于A型手机,小于或等于K的产品应用于B型手机.假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.
(1)若临界值,请估计该公司生产的1000个该型号芯片I级品和1000个Ⅱ级品中应用于A型手机的芯片个数;
(2)设且,现有足够多的芯片I级品 Ⅱ级品,分别应用于A型手机 B型手机各1万部的生产:
方案一:直接将该芯片I级品应用于A型手机,其中该指标小于等于临界值K的芯片会导致芯片生产商每部手机损失800元;直接将该芯片Ⅱ级品应用于B型手机,其中该指标大于临界值K的芯片,会导致芯片生产商每部手机损失400元;
方案二:重新检测芯片I级品,II级品的该项指标,并按规定正确应用于手机型号,会避免方案一的损失费用,但检测费用共需要130万元;
请求出按方案一,芯片生产商损失费用的估计值(单位:万元)的表达式,并从芯片生产商的成本考虑,选择合理的方案.
《第九章统计同步练习卷-2024-2025学年高一数学下学期人教A版(2019)必修第二册》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B A C C B C D AC ABD
题号 11
答案 BCD
1.C
【分析】由分层抽样的适用条件即可判断;
【详解】由题意可知,总体由差异明显的三部分构成,所以选用分层随机抽样法.
故选:C
2.B
【分析】借助平均数、中位数与众数定义计算即可得.
【详解】将这些数从小到大重新排列为:10、12、14、14、15、15、16、17、17、17,
故其中位数,众数,
平均数,
故.
故选:B.
3.A
【分析】根据分层抽样的抽样比即可求解.
【详解】已知甲村和乙村的人数之比是10:9,根据分层抽样,可设甲村被抽取参与调研的村民有10a人,
则乙村被抽取参与调研的村民有9a人,则,解得.
所以参加调研的总人数为.
故选:A
4.C
【分析】由平均数及方差计算公式即可求解.
【详解】由均值和方差公式直接计算.
可估计全班学生数学的平均分为,方差为.
故选:C.
5.C
【分析】先由长方形的面积和为1求出,再由第75百分位数的定义求解;
【详解】因为,所以.
参赛成绩位于内的频率为,
第75百分位数在内,
设为,则,
解得5,即第75百分位数为85,
故选:C.
6.B
【分析】利用分层抽样的平均数公式,列式计算即得.
【详解】依题意,估计总体平均数为.
故选:B
7.C
【分析】由平均数,方差计算公式可判断各选项正误.
【详解】设其他48个数据依次为,
则,因为,
因此平均数不变,即;又由方差计算公式可知:,
,
注意到,则.
故选:C.
8.D
【分析】根据频率分布直方图求出的频率,A项可由各矩形高度可得;B项由频率计算可得;C项分别求出平均数、中位数比较可知;D项由极差定义可得.
【详解】设组的频率为,则由各组频率之和为1可得
,解得;
,,,,各组频率依次为:,
A项, 组频率最大,即成绩在上的人数最多,故A正确;
B项,成绩低于70分的学生频率为,即不低于70分的学生频率为,
所以成绩不低于70分的学生所占比例为,故B正确;
C项,根据频率分布直方图,可得50名学生成绩的平均数是
,
由,故50名学生成绩的中位数为80,
所以50名学生成绩的平均分小于中位数,故选项C正确;
D项,极差为数据中最大值与最小值的差,
已知50名学生的成绩都在区间内,
但成绩的最大值不一定是100,最小值也不一定是,
故极差小于等于,但不一定等于50,故D错误.
故选:D.
9.AC
【分析】根据一组数据的极差,平均数,方差,百分位数的定义依次求解即可.
【详解】由题意可得样本数据的极差为,故A正确;
平均数为,故B错误;
方差为,故C正确;
将样本数据从小到大排列为90,95,100,105,110,因为,所以分位数为,故D错.
故选:AC
10.ABD
【分析】借助频率分布直方图定义计算可得A;借助频率分布直方图计算对应频数可得B、C;借助平均数定义计算可得D.
【详解】对A:,解得,故A正确;
对B:,则约有200人的成绩不低于110分,故B正确;
对C:,故约有120人的成绩低于70分,故C错误;
对D:,
故本次考试的平均分约为93.6分,故D正确.
故选:ABD.
11.BCD
【分析】先由图2计算出食品的开支,再由图1计算出总开支,从而对选项逐一分析即可得解.
【详解】对于C,由图2可知食品的开支为元,
由图1可知食品开支为,所以总开支为元,
则娱乐开支为元,故C正确;
对于A,通信开支为元,娱乐开支比通信开支多元,故A错误;
对于B,日常开支为元,肉类为元,
日常开支比肉类开支多元,故B正确;
对于D,储蓄开支为元,肉类开支占储蓄开支的,故D正确.
故选:BCD.
12.
【分析】先由极差是中位数的2倍得到,再由和为12得到,联立可求出四个数值,即可求第75百分位数.
【详解】这组数据的极差为,中位数为,
根据题意得,即,
又它们的和为12,所以,解得,.
因为为正整数且互不相等,且,
三个数的平均数即中位数,
则得到,.
因为,
所以这4个数据的第75百分位数为.
故答案是:.
13.0.020
【详解】由频率分布直方图的性质,得10(0.005+0.015+a+0.035+0.015+0.010)=1,解得a=0.020.
14.
【分析】利用方差公式可得出的值.
【详解】由题意可知,这个数据的平均数为,
方差为,
解得.
故答案为:.
15.(1)14
(2)16
【分析】(1)先确定样本中男生、女生的人数,再求总样本的平均数.
(2)根据方差的概念,计算总样本的方差.
【详解】(1)样本中男生的人数为:;女生的人数为:.
所以总样本的平均数为:.
(2)记总样本的方差为,
则.
所以,估计高二年级全体学生的百米成绩的方差为16.
16.(1)
(2),
【详解】(1)第六组的频率为,
∴第七组的频率为.
(2)由直方图得,
身高在第一组的频率为,
身高在第二组的频率为,
身高在第三组的频率为,
身高在第四组的频率为,
身高在第五组的频率为,
身高在第六组的频率为,
身高在第七组的频率为,
身高在第八组的频率为,
因为身高在第五组的频率最高,人数最多,
所以众数为.
平均数为:
.
所以估计该校的500名男生的身高的众数为,平均数为.
17.(1)分布表见解析
(2)直方图见解析
(3)234
【分析】(1)根据题中数据,结合频率、频数关系分析运算即可;
(2)根据(1)中数据可得频率分布直方图;
(3)先求成绩在的频率,进而估计人数.
【详解】(1)因为,,,,且所有频率和为1,
据此填满频率分布表,如下表所示:
分组 频数 频率
4 0.08
8 0.16
10 0.2
16 0.32
12 0.24
合计 50 1
(2)根据(1)中数据可得频率分布直方图,如图所示:
(3)由题意可知:成绩在频率为,
估计获得二等奖的学生人数为.
18.(1)7;7;4;1.2
(2)答案见解析
【分析】(1)根据平均数和方差公式计算即可;
(2)由(1)的结论,平均数一样,则通过方差判断其稳定性即可得结果.
【详解】(1),
,
,
.
(2)由(1)知,甲乙射击的平均成绩一样,但乙比甲射击的成绩更稳定,所以选择乙.
19.(1)
(2),应选择方案二
【分析】(1)根据频率分布直方图,即可求解频率,进而可求解,
(2)分别计算两种方案的费用,即可比较作答.
【详解】(1)临界值时,I级品中该指标大于60的频率为,
II级品中该指标大于60的频率为0.1
故该公司生产的1000个该型号芯片I级品和1000个II级品中应用于型手机的芯片个数估计为:
(2)当临界值时,若采用方案一:
I级品中该指标小于或等于临界值的概率为,
可以估计10000部型手机中有部手机芯片应用错误;
II级品中该指标大于临界值的概率为,
可以估计10000部型手机中有部手机芯片应用错误;
故可以估计芯片生产商的损失费用
又采用方案二需要检测费用共130万元
故从芯片生产商的成本考虑,应选择方案二
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章统计同步练习卷-2024-2025学年高一数学下学期人教A版(2019)必修第二册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某政府机关在编人员共100人,其中副处级以上干部10人,一般干部70人,工人20人,上级部门为了了解该机关对政府机构改革的意见,要从中抽取20人,用下列哪种方法最合适( )
A.系统抽样法 B.简单随机抽样法
C.分层随机抽样法 D.随机数法
2.10名工人某天生产同一零件,生产的件数是15、17、14、10、15、17、17、16、14、12,设其平均数为,中位数为,众数为,则有( )
A. B. C. D.
3.为实现乡村生态振兴,走乡村绿色发展之路,某乡政府采用分层抽样的方式从甲村和乙村抽取部分村民参与环保调研,已知甲村和乙村的人数之比是10:9,被抽到的参与环保调研的村民中,甲村比乙村多7人,则参加调研的总人数是( )
A.133 B.170 C.70 D.63
4.为了了解某班学生数学成绩,利用分层随机抽样抽取了一个10人的样本,统计如下表:则可估计全班学生数学的平均分和方差分别为( )
学生数 平均分 方差
男生 6 80 4
女生 4 75 2
A.77.5,9.2 B.77.5,11 C.78,9.2 D.78,11
5.高二年级进行消防知识竞赛,统计所有参赛同学的成绩,成绩都在内,估计所有参赛同学成绩的第75百分位数为( )
A. B. C. D.
6.已知总体划分为3层,按比例用分层随机抽样法抽样,各层的样本量及样本平均数如下表:
分层 样本量 样本平均数
第一层 10 55
第二层 30 75
第三层 10 90
估计总体平均数为( )
A.73 B.74 C.76 D.80
7.已知某人收集一个样本容量为50的一组数据,并求得其平均数为70,方差为75,现发现在收集这些数据时,其中得两个数据记录有误,一个错将80记录为60,另一个错将70记录为90,在对错误的数据进行更正后,重新求得样本的平均数为,方差为,则( )
A. B.
C. D.
8.某校组织50名学生参加庆祝中华人民共和国成立75周年知识竞赛,经统计这50名学生的成绩都在区间内,按分数分成5组:,,,,,得到如图所示的频率分布直方图(不完整),根据图中数据,下列结论错误的是( )
A.成绩在上的人数最多
B.成绩不低于70分的学生所占比例为
C.50名学生成绩的平均分小于中位数
D.50名学生成绩的极差为50
二、多选题
9.已知样本数据90,100,95,110,105,则( )
A.极差为20 B.平均数为103 C.方差为50 D.分位数为97
10.某校1000名学生在高一测试中数学成绩的频率分布直方图如图所示(同一组中的数据用该组区间的中点值作代表),则( )
A.
B.约有200人的成绩不低于110分
C.约有60人的成绩低于70分
D.本次考试的平均分约为93.6分
11.小刘一周的总开支分布如图①所示,该周的食品开支如图②所示,则以下说法正确的是( )
A.娱乐开支比通信开支多5元
B.日常开支比食品中的肉类开支多100元
C.娱乐开支金额为100元
D.肉类开支占储蓄开支的
三、填空题
12.已知互不相等的4个正整数从小到大排序为.若它们的和为12,且这4个数据的极差是中位数的2倍,则这4个数据的第75百分位数为 .
13.已知统计某校1 000名学生的某次数学水平测试成绩得到样本频率分布直方图如图所示,则直方图中实数a的值是 .
14.若一组个数据、、、的平均数为,方差为,则 .
四、解答题
15.在对某高中1500名高二年级学生的百米成绩的调查中,采用按学生性别比例分配的分层随机抽样抽取100人,已知这1500名高二年级学生中男生有900人,且抽取的样本中男生成绩的平均数和方差分别为13.2秒和13.36,女生成绩的平均数和方差分别为15.2秒和17.56.
(1)求抽取的总样本的平均数;
(2)试估计高二年级全体学生的百米成绩的方差.
16.从我校高二年级的名男生中随机抽取名测量身高,被测学生身高全部介于和之间,将测量结果按如下方式分成八组:第一组,第二组,…,第八组,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为人.
(1)求第七组的频率;
(2)估计该校的名男生的身高的众数与平均数;
17.有900名学生参加“环保知识竞赛”,为考察竞赛成绩情况,从中抽取部分学生的成绩(得分均整数,满分为100分)进行统计,请你根据尚未完成并有局部污损的频率分面表和频率分布直方图(如图)解释下列问题.
分组 频数 频率
4 0.08
0.16
10
16 0.32
合计 50
(1)填满频率分布表;
(2)补全频率分布直方图;
(3)若成绩在的学生可以获得二等奖,求获得二等奖的学生人数.
18.有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:
甲:7 8 7 9 5 4 9 10 7 4
乙:9 5 7 8 7 6 8 6 7 7
设甲、乙两名运动员射击平均环数分别记为和,方差分别记为和.
(1)求,,,;
(2)如果你是教练,你如何对这次射击情况作出评价?如果这是一次选拔性考核,你应当如何作出选择?
19.已知某科技公司的某型号芯片的各项指标经过全面检测后,分为I级和Ⅱ级,两种品级芯片的某项指标的频率分布直方图如图所示:
若只利用该指标制定一个标准,需要确定临界值K,将该指标大于K的产品应用于A型手机,小于或等于K的产品应用于B型手机.假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.
(1)若临界值,请估计该公司生产的1000个该型号芯片I级品和1000个Ⅱ级品中应用于A型手机的芯片个数;
(2)设且,现有足够多的芯片I级品 Ⅱ级品,分别应用于A型手机 B型手机各1万部的生产:
方案一:直接将该芯片I级品应用于A型手机,其中该指标小于等于临界值K的芯片会导致芯片生产商每部手机损失800元;直接将该芯片Ⅱ级品应用于B型手机,其中该指标大于临界值K的芯片,会导致芯片生产商每部手机损失400元;
方案二:重新检测芯片I级品,II级品的该项指标,并按规定正确应用于手机型号,会避免方案一的损失费用,但检测费用共需要130万元;
请求出按方案一,芯片生产商损失费用的估计值(单位:万元)的表达式,并从芯片生产商的成本考虑,选择合理的方案.
《第九章统计同步练习卷-2024-2025学年高一数学下学期人教A版(2019)必修第二册》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B A C C B C D AC ABD
题号 11
答案 BCD
1.C
【分析】由分层抽样的适用条件即可判断;
【详解】由题意可知,总体由差异明显的三部分构成,所以选用分层随机抽样法.
故选:C
2.B
【分析】借助平均数、中位数与众数定义计算即可得.
【详解】将这些数从小到大重新排列为:10、12、14、14、15、15、16、17、17、17,
故其中位数,众数,
平均数,
故.
故选:B.
3.A
【分析】根据分层抽样的抽样比即可求解.
【详解】已知甲村和乙村的人数之比是10:9,根据分层抽样,可设甲村被抽取参与调研的村民有10a人,
则乙村被抽取参与调研的村民有9a人,则,解得.
所以参加调研的总人数为.
故选:A
4.C
【分析】由平均数及方差计算公式即可求解.
【详解】由均值和方差公式直接计算.
可估计全班学生数学的平均分为,方差为.
故选:C.
5.C
【分析】先由长方形的面积和为1求出,再由第75百分位数的定义求解;
【详解】因为,所以.
参赛成绩位于内的频率为,
第75百分位数在内,
设为,则,
解得5,即第75百分位数为85,
故选:C.
6.B
【分析】利用分层抽样的平均数公式,列式计算即得.
【详解】依题意,估计总体平均数为.
故选:B
7.C
【分析】由平均数,方差计算公式可判断各选项正误.
【详解】设其他48个数据依次为,
则,因为,
因此平均数不变,即;又由方差计算公式可知:,
,
注意到,则.
故选:C.
8.D
【分析】根据频率分布直方图求出的频率,A项可由各矩形高度可得;B项由频率计算可得;C项分别求出平均数、中位数比较可知;D项由极差定义可得.
【详解】设组的频率为,则由各组频率之和为1可得
,解得;
,,,,各组频率依次为:,
A项, 组频率最大,即成绩在上的人数最多,故A正确;
B项,成绩低于70分的学生频率为,即不低于70分的学生频率为,
所以成绩不低于70分的学生所占比例为,故B正确;
C项,根据频率分布直方图,可得50名学生成绩的平均数是
,
由,故50名学生成绩的中位数为80,
所以50名学生成绩的平均分小于中位数,故选项C正确;
D项,极差为数据中最大值与最小值的差,
已知50名学生的成绩都在区间内,
但成绩的最大值不一定是100,最小值也不一定是,
故极差小于等于,但不一定等于50,故D错误.
故选:D.
9.AC
【分析】根据一组数据的极差,平均数,方差,百分位数的定义依次求解即可.
【详解】由题意可得样本数据的极差为,故A正确;
平均数为,故B错误;
方差为,故C正确;
将样本数据从小到大排列为90,95,100,105,110,因为,所以分位数为,故D错.
故选:AC
10.ABD
【分析】借助频率分布直方图定义计算可得A;借助频率分布直方图计算对应频数可得B、C;借助平均数定义计算可得D.
【详解】对A:,解得,故A正确;
对B:,则约有200人的成绩不低于110分,故B正确;
对C:,故约有120人的成绩低于70分,故C错误;
对D:,
故本次考试的平均分约为93.6分,故D正确.
故选:ABD.
11.BCD
【分析】先由图2计算出食品的开支,再由图1计算出总开支,从而对选项逐一分析即可得解.
【详解】对于C,由图2可知食品的开支为元,
由图1可知食品开支为,所以总开支为元,
则娱乐开支为元,故C正确;
对于A,通信开支为元,娱乐开支比通信开支多元,故A错误;
对于B,日常开支为元,肉类为元,
日常开支比肉类开支多元,故B正确;
对于D,储蓄开支为元,肉类开支占储蓄开支的,故D正确.
故选:BCD.
12.
【分析】先由极差是中位数的2倍得到,再由和为12得到,联立可求出四个数值,即可求第75百分位数.
【详解】这组数据的极差为,中位数为,
根据题意得,即,
又它们的和为12,所以,解得,.
因为为正整数且互不相等,且,
三个数的平均数即中位数,
则得到,.
因为,
所以这4个数据的第75百分位数为.
故答案是:.
13.0.020
【详解】由频率分布直方图的性质,得10(0.005+0.015+a+0.035+0.015+0.010)=1,解得a=0.020.
14.
【分析】利用方差公式可得出的值.
【详解】由题意可知,这个数据的平均数为,
方差为,
解得.
故答案为:.
15.(1)14
(2)16
【分析】(1)先确定样本中男生、女生的人数,再求总样本的平均数.
(2)根据方差的概念,计算总样本的方差.
【详解】(1)样本中男生的人数为:;女生的人数为:.
所以总样本的平均数为:.
(2)记总样本的方差为,
则.
所以,估计高二年级全体学生的百米成绩的方差为16.
16.(1)
(2),
【详解】(1)第六组的频率为,
∴第七组的频率为.
(2)由直方图得,
身高在第一组的频率为,
身高在第二组的频率为,
身高在第三组的频率为,
身高在第四组的频率为,
身高在第五组的频率为,
身高在第六组的频率为,
身高在第七组的频率为,
身高在第八组的频率为,
因为身高在第五组的频率最高,人数最多,
所以众数为.
平均数为:
.
所以估计该校的500名男生的身高的众数为,平均数为.
17.(1)分布表见解析
(2)直方图见解析
(3)234
【分析】(1)根据题中数据,结合频率、频数关系分析运算即可;
(2)根据(1)中数据可得频率分布直方图;
(3)先求成绩在的频率,进而估计人数.
【详解】(1)因为,,,,且所有频率和为1,
据此填满频率分布表,如下表所示:
分组 频数 频率
4 0.08
8 0.16
10 0.2
16 0.32
12 0.24
合计 50 1
(2)根据(1)中数据可得频率分布直方图,如图所示:
(3)由题意可知:成绩在频率为,
估计获得二等奖的学生人数为.
18.(1)7;7;4;1.2
(2)答案见解析
【分析】(1)根据平均数和方差公式计算即可;
(2)由(1)的结论,平均数一样,则通过方差判断其稳定性即可得结果.
【详解】(1),
,
,
.
(2)由(1)知,甲乙射击的平均成绩一样,但乙比甲射击的成绩更稳定,所以选择乙.
19.(1)
(2),应选择方案二
【分析】(1)根据频率分布直方图,即可求解频率,进而可求解,
(2)分别计算两种方案的费用,即可比较作答.
【详解】(1)临界值时,I级品中该指标大于60的频率为,
II级品中该指标大于60的频率为0.1
故该公司生产的1000个该型号芯片I级品和1000个II级品中应用于型手机的芯片个数估计为:
(2)当临界值时,若采用方案一:
I级品中该指标小于或等于临界值的概率为,
可以估计10000部型手机中有部手机芯片应用错误;
II级品中该指标大于临界值的概率为,
可以估计10000部型手机中有部手机芯片应用错误;
故可以估计芯片生产商的损失费用
又采用方案二需要检测费用共130万元
故从芯片生产商的成本考虑,应选择方案二
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
