沪教版七年级数学下册 17.1三角形的有关概念 试题(含详解)
文档属性
| 名称 | 沪教版七年级数学下册 17.1三角形的有关概念 试题(含详解) | 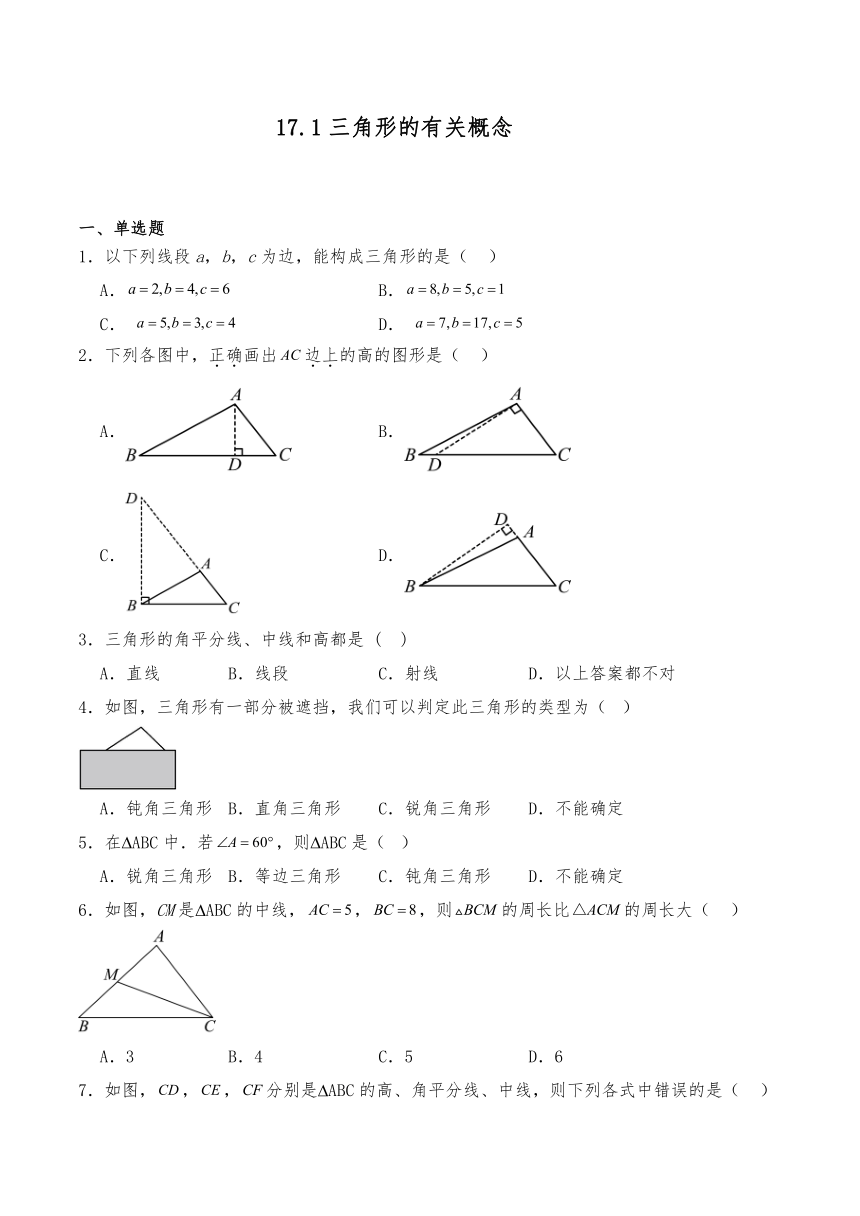 | |
| 格式 | docx | ||
| 文件大小 | 835.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-02 13:55:56 | ||
图片预览




文档简介
17.1三角形的有关概念
一、单选题
1.以下列线段a,b,c为边,能构成三角形的是( )
A. B.
C. D.
2.下列各图中,正确画出边上的高的图形是( )
A. B.
C. D.
3.三角形的角平分线、中线和高都是 ( )
A.直线 B.线段 C.射线 D.以上答案都不对
4.如图,三角形有一部分被遮挡,我们可以判定此三角形的类型为( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.不能确定
5.在 ABC中.若,则 ABC是( )
A.锐角三角形 B.等边三角形 C.钝角三角形 D.不能确定
6.如图,CM是 ABC的中线,,,则的周长比的周长大( )
A.3 B.4 C.5 D.6
7.如图,,,分别是 ABC的高、角平分线、中线,则下列各式中错误的是( )
A. B. C. D.
8.如图,嘉琪任意剪了一张钝角三角形纸片(是钝角),他打算用折叠的方法折出的角平分线、边上的中线和高线,能折出的是( )
A.边上的中线和高线 B.的角平分线和边上的高线
C.的角平分线和边上的中线 D.的角平分线、边上的中线和高线
二、填空题
9.如图,生活中都把自行车的几根梁做成三角形的支架,这是因为 .
10.三角形的三边分别为 5, ,9,则的取值范围为 .
11.如图所示:在Rt△ABC中,∠A=90°,边AB上的高是 .
12.若一个三角形三边的长度比为,周长为 cm,则这个三角形三边的长分别为 ,按边分,这个三角形是 三角形.
13.如图,在 ABC中,于点,,,,边上的高是.则 .
14.如图,在 ABC中,是边上的高,且,如果,那么 .
15.如图,在 ABC中,为上一点,为上一点,,连接交于点.若则的面积为 .
16.如图,对面积为的逐次进行操作:第一次操作,分别延长、、至点、、,使得,,,顺次连接、、,得到,记其面积为;第二次操作,分别延长、、至点、、,使得、、,顺次连接、,得到,记其面积为,,按此规律继续下去,可得到,则其面积 .
三、解答题
17.(1)图中共有_________个三角形,它们分别是_________;
(2)以为边的三角形有_________;
(3)分别是,, ABC中_________,_________,_________边的对角;
(4)是_________,_________,_________的内角;是_________,_________的内角.
18.若a、b、c是 ABC的三边的长,化简.
19.下列各组中的数分别表示三条线段的长度,试判断以下列各组线段为边是否能组成三角形.
(1),,;
(2),,;
(3),,(,).
20.如图,已知 ABC,根据下列要求作图并回答问题:
(1)作边上的高;
(2)过点D作直线的垂线,垂足为E;
(3)点B到直线的距离是线段_______的长度,(不要求写画法,只需写出结论即可)
21.根据要求作图并写好结论:
(1)画三角形,使得的长度等于厘米,,;
(2)在三角形中,作出的角平分线;
(3)在三角形中,作出边上中线.
22.已知三角形纸片(如图),将纸片折叠,使点与点重合,折痕分别与边、交于点、,点关于直线的对称点为点.
(1)画出直线和点;
(2)连接、,如果,求的度数;
(3)连接、、,如果,且的面积为4,求 ABC的面积.
23.阅读与思考:数学活动课上,老师提出如下问题:如图1,在中,为边上的中线.求证:.小明给出如下证明过程.
证明:如图2,过点作于点.
为边上的中线,
① .
,② ,
.
(1)请将小明横线处的证明过程补充完整.
(2)经过探究,小明还发现:如图3,若为边上的任意一点,则,请写出证明过程.
(3)如图4, ABC的面积为,是边上靠近点的三等分点,是边上靠近点的四等分点,则 ADE的面积为______.
答案
一、单选题
1.C
【分析】本题主要考查了三角形的三边关系,解题的关键在于能够熟练掌握构成三角形的条件.根据三角形三边的关系:两边之和大于第三边,两边之差小于第三边,进行求解判断即可.
【解析】解:A、,故不能构成三角形,不符合题意;
B、,故不能构成三角形,不符合题意;
C、,故能构成三角形,符合题意;
D、,故不能构成三角形,不符合题意.
故选:C.
2.D
【分析】本题主要考查了三角形高的定义,掌握三角形高的定义是解题的关键.根据“点到直线的距离即为边上的高”,即可求解.
【解析】解:边上的高为点到直线的距离,即,
故选:D.
3.B
【分析】根据三角形的角平分线、中线和高定义判断即可.
【解析】解:三角形的角平分线、中线、高都是线段.
故选:B.
4.A
【分析】本题考查了三角形的分类,根据三角形露出的部分为钝角,即可求解.
【解析】解:依题意,三角形露出的部分为钝角,
∴我们可以判定此三角形的类型为钝角三角形
故选:A.
5.D
【分析】本题考查了三角形的分类,根据三角形的分类即可求解,掌握三角形的分类是解题的关键.
【解析】解:∵,和无法确定,
∴ ABC可能是锐角三角形,等边三角形,直角三角形,钝角三角形,
故选:.
6.A
【分析】本题考查三角形中线,,熟知三角形一边的中点与此边所对顶点的连线叫做三角形的中线是此题的关键.
【解析】∵为的边上的中线,
∴,
∴的周长与的周长大:,
故选:A.
7.C
【分析】根据三角形高,中线,角平分线的定义进行逐一判断即可.
【解析】解:A、∵是的中线,
∴,原结论正确,不符合题意;
B、∵是 ABC的角平分线,
∴,原结论正确,不符合题意;
C、∵是 ABC的中线,
∴,
∴,原结论错误,符合题意;
D、∵是 ABC的高,
∴,原结论正确,不符合题意;
故选C.
8.C
【分析】由折叠的性质可求解.
【解析】解:当与重合时,折痕是的角平分线;
当点A与点B重合时,折叠是的中垂线,
故选:C.
二、填空题
9.三角形具有稳定性
【分析】本题考查三角形稳定性的实际应用.熟练掌握常见的三角形的稳定性在实际生活中的应用,如钢架桥、房屋架梁等是解题的关键.根据三角形具有稳定性解答.
【解析】解:生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有稳定性.
故答案为:三角形具有稳定性.
10.
【分析】根据三角形三边关系解答.
【解析】由题意得:,
解得:,
故答案为:.
11.AC
【分析】根据三角形的高的定义(从三角形一个顶点向它的对边作一条垂线,三角形顶点和它对边垂足之间的线段称为三角形这条边上的高)即可得.
【解析】,
由三角形的高的定义可知,线段为中边上的高
故答案为:
12. 8 cm,12 cm,12 cm 等腰
【分析】本题考查了三角形的分类,根据题意设三角形三边的长度比为,即可列方程求解.
【解析】解:设三角形三边的长度比为,
则:,
解得:
∴
故答案为:①8 cm,12 cm,12 cm②等腰
13.
【分析】本题主要考查了求三角形的高,熟记三角形的面积公式是解题的关键.
【解析】解:∵,
∴,
故答案为:.
14.
【分析】根据,和,求出,利用,进行计算即可.
【解析】解:∵在 ABC中,是边上的高,且,
∴,
∴,
∴;
故答案为:.
15.5
【分析】本题考查的是三角形的面积,与三角形的高有关的计算,理解同高的两个三角形的面积之间的关系是解本题的关键,由,可得,从而可得答案.
【解析】解:∵,,
∴,,
∴.
故答案为:5.
16.361
【分析】根据三角形等高时底之比等于面积比得出的面积为面积的两倍,则的面积是的2倍…,以此类推,得出的面积.
【解析】
连接, , ,根据,的面积为的2倍,所以的面积为2;同理的面积为的2倍,所以的面积为4;
以此类推:的面积为2,的面积为4,的面积为2,的面积为4
∴,即面积为面积的19倍,以此类推的面积为面积的倍,所以.
故答案为:361
三、解答题
17.解:(1)图中的三角形为:,, ABC, ADE,,,共6个;
(2)以为边的三角形有, ADE,;
(3)分别是,, ABC中,,边的对角;
(4)是,, ABC的内角,是 ADE,的内角.
故答案为:6;,, ABC, ADE,,;, ADE,;,,;,, ABC; ADE,.
18.解:∵a、b、c是的三边,
∴,
∴,
∴
.
19.(1)解:,
不能组成三角形;
(2)解:,
能组成三角形;
(3)解:,,
、为较短边的长度,
又,
不能组成三角形.
20.(1)解:如图,线段即为所求.
(2)如图,线段即为所求.
(3)到直线的距离是线段的长度.
故答案为:.
21.(1)如图,即为所求;
(2)如图,射线即为所求;
(3)如图,线段即为所求.
22.(1)解:如图,直线和点即为所求;
(2)解:∵点关于直线的对称点为点,
∴,
∵,
∴,
∴,
∴;
(3)解:如图,
由折叠的性质得:,,
∵,
∴,
∴,
∴,
∵,
∴.
23.(1)证明:如图2,过点作于点.
为边上的中线,
.
,,
.
故答案为:,;
(2)证明:如图3,过点作于点.
,,
∴;
(3)解:同理(2)得,,
∵ ABC的面积为,是边上靠近点的三等分点,
∴,
∴,
∵是边上靠近点的四等分点,
∴,
∴,
故答案为:12.
一、单选题
1.以下列线段a,b,c为边,能构成三角形的是( )
A. B.
C. D.
2.下列各图中,正确画出边上的高的图形是( )
A. B.
C. D.
3.三角形的角平分线、中线和高都是 ( )
A.直线 B.线段 C.射线 D.以上答案都不对
4.如图,三角形有一部分被遮挡,我们可以判定此三角形的类型为( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.不能确定
5.在 ABC中.若,则 ABC是( )
A.锐角三角形 B.等边三角形 C.钝角三角形 D.不能确定
6.如图,CM是 ABC的中线,,,则的周长比的周长大( )
A.3 B.4 C.5 D.6
7.如图,,,分别是 ABC的高、角平分线、中线,则下列各式中错误的是( )
A. B. C. D.
8.如图,嘉琪任意剪了一张钝角三角形纸片(是钝角),他打算用折叠的方法折出的角平分线、边上的中线和高线,能折出的是( )
A.边上的中线和高线 B.的角平分线和边上的高线
C.的角平分线和边上的中线 D.的角平分线、边上的中线和高线
二、填空题
9.如图,生活中都把自行车的几根梁做成三角形的支架,这是因为 .
10.三角形的三边分别为 5, ,9,则的取值范围为 .
11.如图所示:在Rt△ABC中,∠A=90°,边AB上的高是 .
12.若一个三角形三边的长度比为,周长为 cm,则这个三角形三边的长分别为 ,按边分,这个三角形是 三角形.
13.如图,在 ABC中,于点,,,,边上的高是.则 .
14.如图,在 ABC中,是边上的高,且,如果,那么 .
15.如图,在 ABC中,为上一点,为上一点,,连接交于点.若则的面积为 .
16.如图,对面积为的逐次进行操作:第一次操作,分别延长、、至点、、,使得,,,顺次连接、、,得到,记其面积为;第二次操作,分别延长、、至点、、,使得、、,顺次连接、,得到,记其面积为,,按此规律继续下去,可得到,则其面积 .
三、解答题
17.(1)图中共有_________个三角形,它们分别是_________;
(2)以为边的三角形有_________;
(3)分别是,, ABC中_________,_________,_________边的对角;
(4)是_________,_________,_________的内角;是_________,_________的内角.
18.若a、b、c是 ABC的三边的长,化简.
19.下列各组中的数分别表示三条线段的长度,试判断以下列各组线段为边是否能组成三角形.
(1),,;
(2),,;
(3),,(,).
20.如图,已知 ABC,根据下列要求作图并回答问题:
(1)作边上的高;
(2)过点D作直线的垂线,垂足为E;
(3)点B到直线的距离是线段_______的长度,(不要求写画法,只需写出结论即可)
21.根据要求作图并写好结论:
(1)画三角形,使得的长度等于厘米,,;
(2)在三角形中,作出的角平分线;
(3)在三角形中,作出边上中线.
22.已知三角形纸片(如图),将纸片折叠,使点与点重合,折痕分别与边、交于点、,点关于直线的对称点为点.
(1)画出直线和点;
(2)连接、,如果,求的度数;
(3)连接、、,如果,且的面积为4,求 ABC的面积.
23.阅读与思考:数学活动课上,老师提出如下问题:如图1,在中,为边上的中线.求证:.小明给出如下证明过程.
证明:如图2,过点作于点.
为边上的中线,
① .
,② ,
.
(1)请将小明横线处的证明过程补充完整.
(2)经过探究,小明还发现:如图3,若为边上的任意一点,则,请写出证明过程.
(3)如图4, ABC的面积为,是边上靠近点的三等分点,是边上靠近点的四等分点,则 ADE的面积为______.
答案
一、单选题
1.C
【分析】本题主要考查了三角形的三边关系,解题的关键在于能够熟练掌握构成三角形的条件.根据三角形三边的关系:两边之和大于第三边,两边之差小于第三边,进行求解判断即可.
【解析】解:A、,故不能构成三角形,不符合题意;
B、,故不能构成三角形,不符合题意;
C、,故能构成三角形,符合题意;
D、,故不能构成三角形,不符合题意.
故选:C.
2.D
【分析】本题主要考查了三角形高的定义,掌握三角形高的定义是解题的关键.根据“点到直线的距离即为边上的高”,即可求解.
【解析】解:边上的高为点到直线的距离,即,
故选:D.
3.B
【分析】根据三角形的角平分线、中线和高定义判断即可.
【解析】解:三角形的角平分线、中线、高都是线段.
故选:B.
4.A
【分析】本题考查了三角形的分类,根据三角形露出的部分为钝角,即可求解.
【解析】解:依题意,三角形露出的部分为钝角,
∴我们可以判定此三角形的类型为钝角三角形
故选:A.
5.D
【分析】本题考查了三角形的分类,根据三角形的分类即可求解,掌握三角形的分类是解题的关键.
【解析】解:∵,和无法确定,
∴ ABC可能是锐角三角形,等边三角形,直角三角形,钝角三角形,
故选:.
6.A
【分析】本题考查三角形中线,,熟知三角形一边的中点与此边所对顶点的连线叫做三角形的中线是此题的关键.
【解析】∵为的边上的中线,
∴,
∴的周长与的周长大:,
故选:A.
7.C
【分析】根据三角形高,中线,角平分线的定义进行逐一判断即可.
【解析】解:A、∵是的中线,
∴,原结论正确,不符合题意;
B、∵是 ABC的角平分线,
∴,原结论正确,不符合题意;
C、∵是 ABC的中线,
∴,
∴,原结论错误,符合题意;
D、∵是 ABC的高,
∴,原结论正确,不符合题意;
故选C.
8.C
【分析】由折叠的性质可求解.
【解析】解:当与重合时,折痕是的角平分线;
当点A与点B重合时,折叠是的中垂线,
故选:C.
二、填空题
9.三角形具有稳定性
【分析】本题考查三角形稳定性的实际应用.熟练掌握常见的三角形的稳定性在实际生活中的应用,如钢架桥、房屋架梁等是解题的关键.根据三角形具有稳定性解答.
【解析】解:生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有稳定性.
故答案为:三角形具有稳定性.
10.
【分析】根据三角形三边关系解答.
【解析】由题意得:,
解得:,
故答案为:.
11.AC
【分析】根据三角形的高的定义(从三角形一个顶点向它的对边作一条垂线,三角形顶点和它对边垂足之间的线段称为三角形这条边上的高)即可得.
【解析】,
由三角形的高的定义可知,线段为中边上的高
故答案为:
12. 8 cm,12 cm,12 cm 等腰
【分析】本题考查了三角形的分类,根据题意设三角形三边的长度比为,即可列方程求解.
【解析】解:设三角形三边的长度比为,
则:,
解得:
∴
故答案为:①8 cm,12 cm,12 cm②等腰
13.
【分析】本题主要考查了求三角形的高,熟记三角形的面积公式是解题的关键.
【解析】解:∵,
∴,
故答案为:.
14.
【分析】根据,和,求出,利用,进行计算即可.
【解析】解:∵在 ABC中,是边上的高,且,
∴,
∴,
∴;
故答案为:.
15.5
【分析】本题考查的是三角形的面积,与三角形的高有关的计算,理解同高的两个三角形的面积之间的关系是解本题的关键,由,可得,从而可得答案.
【解析】解:∵,,
∴,,
∴.
故答案为:5.
16.361
【分析】根据三角形等高时底之比等于面积比得出的面积为面积的两倍,则的面积是的2倍…,以此类推,得出的面积.
【解析】
连接, , ,根据,的面积为的2倍,所以的面积为2;同理的面积为的2倍,所以的面积为4;
以此类推:的面积为2,的面积为4,的面积为2,的面积为4
∴,即面积为面积的19倍,以此类推的面积为面积的倍,所以.
故答案为:361
三、解答题
17.解:(1)图中的三角形为:,, ABC, ADE,,,共6个;
(2)以为边的三角形有, ADE,;
(3)分别是,, ABC中,,边的对角;
(4)是,, ABC的内角,是 ADE,的内角.
故答案为:6;,, ABC, ADE,,;, ADE,;,,;,, ABC; ADE,.
18.解:∵a、b、c是的三边,
∴,
∴,
∴
.
19.(1)解:,
不能组成三角形;
(2)解:,
能组成三角形;
(3)解:,,
、为较短边的长度,
又,
不能组成三角形.
20.(1)解:如图,线段即为所求.
(2)如图,线段即为所求.
(3)到直线的距离是线段的长度.
故答案为:.
21.(1)如图,即为所求;
(2)如图,射线即为所求;
(3)如图,线段即为所求.
22.(1)解:如图,直线和点即为所求;
(2)解:∵点关于直线的对称点为点,
∴,
∵,
∴,
∴,
∴;
(3)解:如图,
由折叠的性质得:,,
∵,
∴,
∴,
∴,
∵,
∴.
23.(1)证明:如图2,过点作于点.
为边上的中线,
.
,,
.
故答案为:,;
(2)证明:如图3,过点作于点.
,,
∴;
(3)解:同理(2)得,,
∵ ABC的面积为,是边上靠近点的三等分点,
∴,
∴,
∵是边上靠近点的四等分点,
∴,
∴,
故答案为:12.
同课章节目录
