沪教版七年级数学下册 16.2.2平行线的判定定理 试题(含详解)
文档属性
| 名称 | 沪教版七年级数学下册 16.2.2平行线的判定定理 试题(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 877.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-02 13:56:51 | ||
图片预览


文档简介
16.2.2平行线的判定定理
一、单选题
1.如图,直线,被第三条直线所截.由“”,得到“”的依据是( )
A.两直线平行,同位角相等 B.同位角相等,两直线平行
C.两直线平行,内错角相等 D.内错角相等,两直线平行
2.如图,下列条件中,能判定直线的是( )
A. B. C. D.
3.如图,已知,要使, 则需具备的另一个条件是( )
A. B. C. D.
4.如图所示,已知,那么下列结论正确的是( )
A. B. C. D.
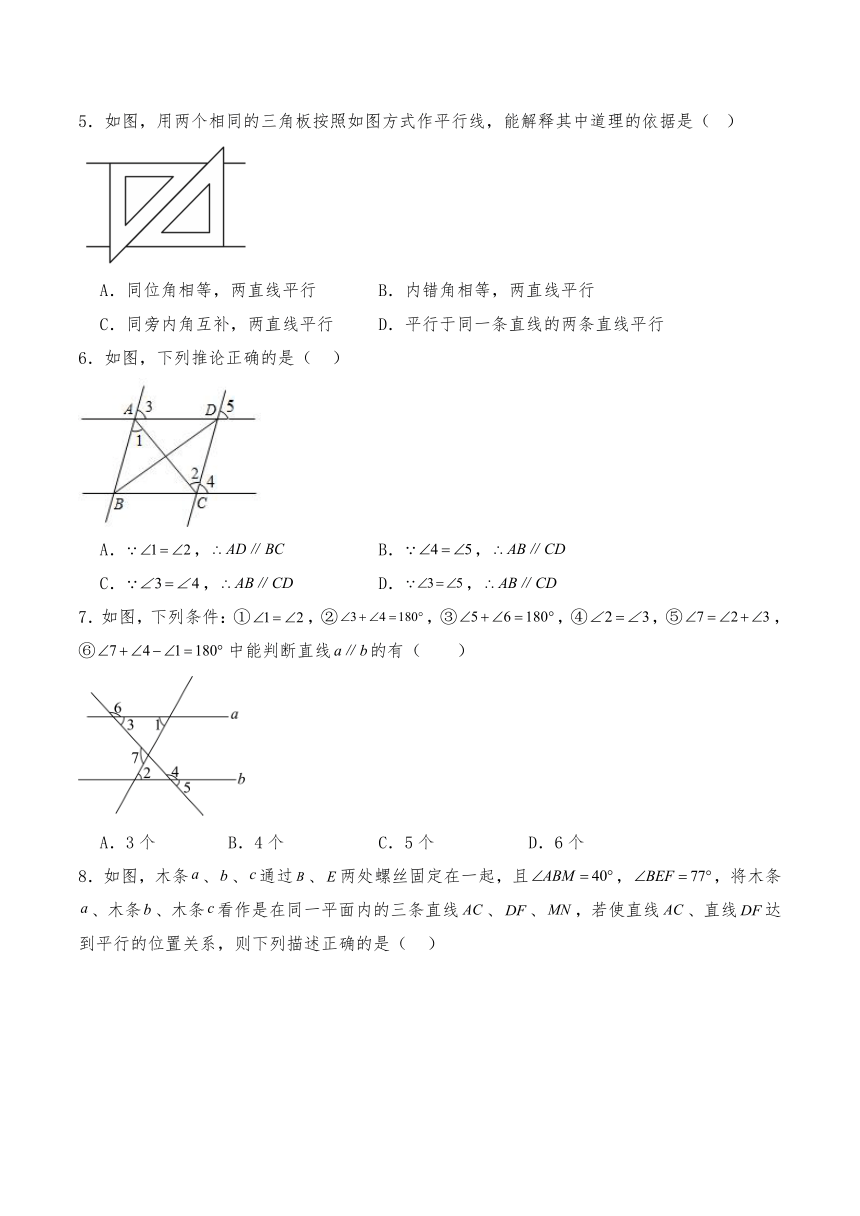
5.如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.平行于同一条直线的两条直线平行
6.如图,下列推论正确的是( )
A., B.,
C., D.,
7.如图,下列条件:①,②,③,④,⑤,⑥中能判断直线的有( )
A.3个 B.4个 C.5个 D.6个
8.如图,木条、、通过、两处螺丝固定在一起,且,,将木条、木条、木条看作是在同一平面内的三条直线、、,若使直线、直线达到平行的位置关系,则下列描述正确的是( )
A.木条、固定不动,木条绕点顺时针旋转
B.木条、固定不动,木条绕点逆时针旋转
C.木条、固定不动,木条绕点逆时针旋转
D.木条、固定不动,木条绕点顺时针旋转
9.如图,下列条件中:①,②,③,④,能判断的有( )
A.1个 B.2个 C.3个 D.4个
10.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度可以是( )
A.第一次向右拐40°,第二次向左拐140° B.第一次向左拐40°,第二次向右拐40°
C.第一次向左拐40°,第二次向右拐140° D.第一次向右拐40°,第二次向右拐40°
二、填空题
11.如图,填空:
(1)若∠A=∠3,则____∥_____,理由是______;
(2)若∠2=∠E,则____∥___,理由是____;
(3)若∠A+∠ABE=180°,则____∥___,理由是____;
(4)若∠2=∠____,则DA∥EB,理由是____;
(5)若∠DBC+∠_____=180°,则DB∥EC,理由是____;
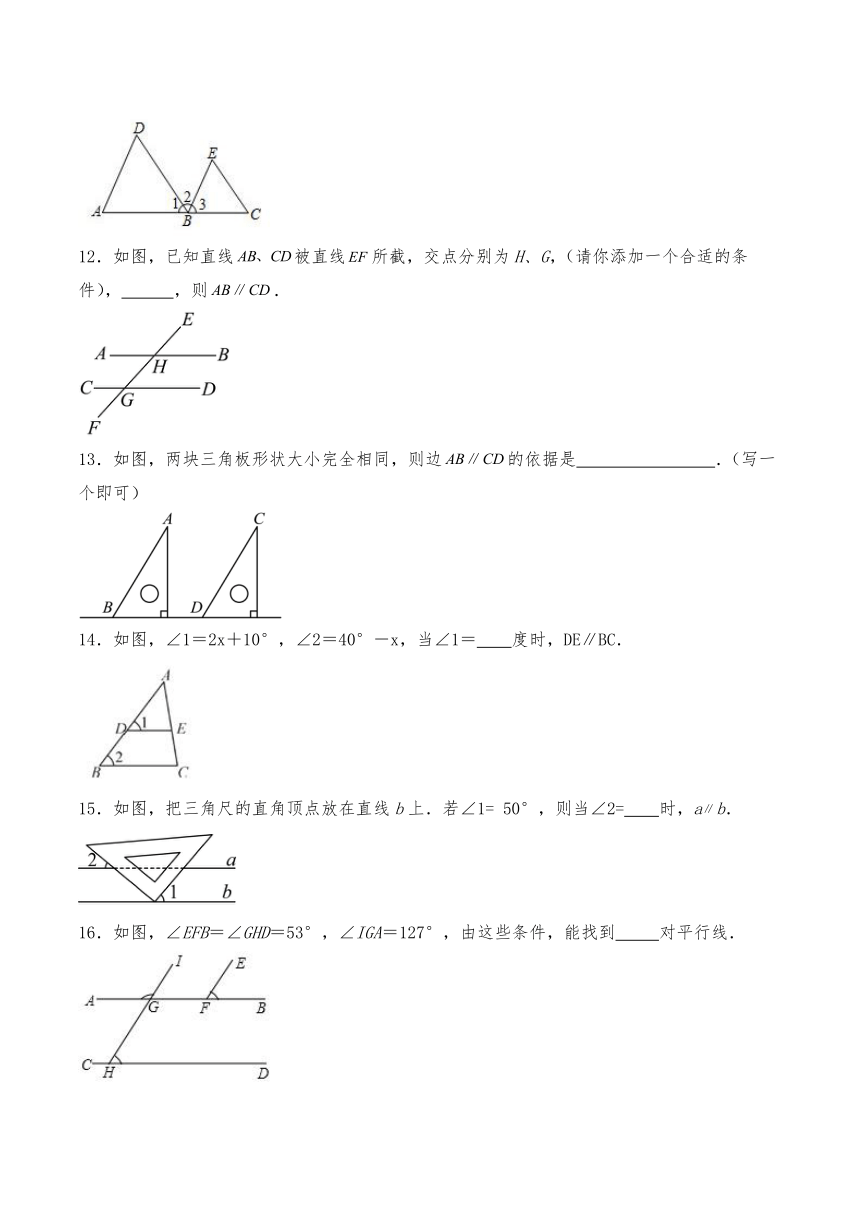
12.如图,已知直线被直线所截,交点分别为H、G,(请你添加一个合适的条件), ,则.
13.如图,两块三角板形状大小完全相同,则边的依据是 .(写一个即可)
14.如图,∠1=2x+10°,∠2=40°-x,当∠1= 度时,DE∥BC.
15.如图,把三角尺的直角顶点放在直线b上.若∠1= 50°,则当∠2= 时,ab.
16.如图,∠EFB=∠GHD=53°,∠IGA=127°,由这些条件,能找到 对平行线.
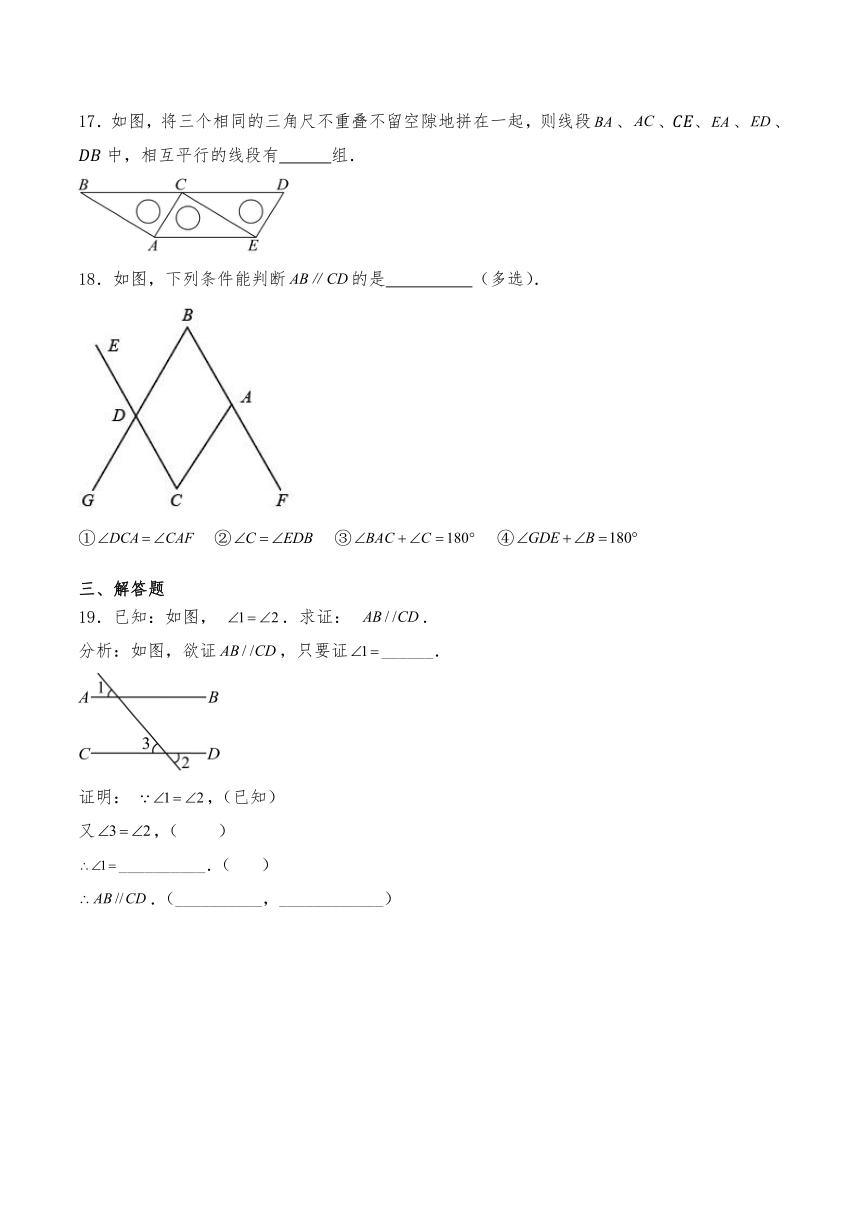
17.如图,将三个相同的三角尺不重叠不留空隙地拼在一起,则线段、、、、、中,相互平行的线段有 组.
18.如图,下列条件能判断的是 (多选).
① ② ③ ④
三、解答题
19.已知:如图, .求证: .
分析:如图,欲证,只要证______.
证明: ,(已知)
又,( )
__________.( )
.(__________,____________)
20.如图,是上一点,是上一点,是延长线上一点.
(1)如果,可以判断哪两条直线平行?为什么?
(2)如果,可以判断哪两条直线平行?为什么?
(3)如果,可以判断哪两条直线平行?为什么?
21.已知:如图,直线被所截, ,
求证: .
证法1:如图, 与交于
( )
又( )
( )
( )
证法2:如图,
( )
又( )
( )
( )
证法3:如图,
( )
( )
又( )
( )
( )
22.如图,已知,.判断与的位置关系,并证明.
23.已知:如图,,和互余,于点G,求证:.(推理过程请注明理由)
24.如图,已知,平分,平分,且,请填写说明DE∥BF的理由的依据.
解:因为平分,平分(已知)
所以,(______)
因为(已知)
所以(______)
因为(______)
所以(______)
所以DEBF(______)
25.如图,,求证:,请将证明过程填写完整.
证明:∵(已知)
又∵( )
∴________,
∴____________( )
∴______________( )
又∵(已知)
∴________________,
∴( )
26.完成下面的证明:
如图,平分,平分,且.
求证:.
证明:∵平分(已知),
∴( ).
又∵平分( ),
∴______( ).
( ).
又∵(已知),
(______)( ).
∴( ).
答案
一、单选题
1.D
【分析】本题考查了平行线的判定,熟练掌握内错角相等,两直线平行是解题的关键.
根据平行线的判定判断作答即可.
【解析】解:∵,
∴(内错角相等,两直线平行),
故选:D.
2.B
【分析】本题考查的是平行线的判定,熟知平行线的判定定理是解答此题的关键.根据平行线的判定定理对各小题进行逐一判断即可.
【解析】解:A.,不能判定,不符合题意;
B.,同位角相等,则,符合题意;
C.,不能判定,不符合题意;
D.,不能判定,不符合题意.
故选:B.
3.D
【分析】根据平行线的判定方法,求解即可.
【解析】解:∵
∴
当时,,,可得
故选:D
4.B
【分析】本题考查了平行线的判定,解答本题的关键是掌握平行线的判定定理:内错角相等,两直线平行.和是直线、被直线所截的内错角,若,则.
【解析】解:,
(内错角相等,两直线平行)
故选:B
5.B
【分析】本题考查平行线的判定,根据内错角相等,两直线平行,进行判断即可.
【解析】解:如图,由题意,得:,
∴(内错角相等,两直线平行);
故选B.
6.D
【分析】利用平行线的判定方法判断即可得到结果.
【解析】解:A、,
∴(内错角相等,两直线平行),不符合题意;
B、,
∴(同位角相等,两直线平行),不符合题意;
C、由无法得到,不符合题意;
D、,
∴(同位角相等,两直线平行),符合题意.
故选:D.
7.C
【分析】本题主要考查了平行线的判定.同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.依据平行线的判定方法即可得出结论.
【解析】解:①由,可得;
②由,可得;
③由,,可得,即可得到;
④由,不能得到;
⑤由,可得,即可得到;
⑥由,,可得,即可得到;
故选:C.
8.C
【分析】要使直线、直线达到平行的位置关系,则要使(二者是内错角)或(二者是同旁内角),据此逐一判断即可
【解析】解:A、木条、固定不动,木条绕点顺时针旋转,则此时,则与不平行,不符合题意;
B、木条、固定不动,木条绕点逆时针旋转, 则此时,即,则与不平行,不符合题意;
C、木条、固定不动,木条绕点逆时针旋转,则,则与平行,符合题意;
D、木条、固定不动,木条绕点顺时针旋转,则,即,则与不平行,符不合题意;
故选C.
9.C
【分析】由平行线的判定定理进行判断,即可得到答案.
【解析】解:,则;故①符合题意;
,则;故②不符合题意;
,则;故③符合题意;
由,,则,得;故④符合题意;
故选:C
10.B
【分析】两次拐弯后,行驶方向与原来相同,说明两次拐弯后的方向是平行的.对题中的四个选项提供的条件,运用平行线的判定进行判断,能判定两直线平行者即为正确答案.
【解析】A、如图1:∵∠1=40°,∠2=140°,
∴AB与CD不平行;
故本选项错误;
B、如图2:∵∠1=40°,∠2=40°,
∴∠1=∠2,
∴AB与CD平行;
故本选项正确;
C、如图3:∵∠1=40°,∠2=140°,
∴∠1≠∠2,
∴AB不平行CD;
故本选项错误;
D、如图4:∠1=40°,∠2=40°,
∴∠3=140°,
∴∠1≠∠3,
∴AB与CD不平行;
故本选项错误.
故选B.
二、填空题
11.
【解析】(1)若∠A=∠3,则_AD__∥__BE__,理由是;(同位角相等,两直线平行);
(2)若∠2=∠E,则__BD__∥_CE__,理由是(内错角相等,两直线平行);
(3)若∠A+∠ABE=180°,则_AD___∥__BE_,理由是(同旁内角互补,两直线平行);
(4)若∠2=∠_D___,则DA∥EB,理由是(内错角相等,两直线平行);
(5)若∠DBC+∠_C_=180°,则DB∥EC,理由是(同旁内角互补,两直线平行);
故答案为(1). AD (2). BE (3). 同位角相等,两直线平行; (4). BD, (5)CE, (6)内错角相等,两直线平行; (7). AD, (8)BE, (9)同旁内角互补,两直线平行; (10). D (11). 内错角相等,两直线平行; (12).C, (13) 同旁内角互补,两直线平行.
12.(答案不唯一)
【分析】本题考查平行线的判定,根据平行线的判定定理添加条件即可.
【解析】解:添加,根据“同位角相等,两直线平行”可得;
添加,根据“内错角相等,两直线平行”可得;
添加,根据“同旁内角互补,两直线平行”可得;
故答案为:(答案不唯一).
13.同位角相等,两直线平行(答案不唯一)
【分析】利用平行线的判定方法即可解决问题.
【解析】解:依题意,
∴(同位角相等,两直线平行)
故答案为:同位角相等,两直线平行(答案不唯一).
14.30
【分析】根据平行线的判定定理得出当∠1=∠2时,DE∥BC,推出方程2x+10=40-x,求出x的值,即可求出∠1.
【解析】当∠1=∠2时,DE∥BC,
即2x+10=40 x,
解得:x=10,
∠1=(2×10+10)度=30度,
故答案为30.
15.40°
【分析】根据三角尺的直角顶点在直线b上,∠1=50°,即可得到∠3=180° 90° ∠1=40°,再根据ab,即可得到∠2=∠3=40°.
【解析】解:如图,
∵三角尺的直角顶点在直线b上,∠1=20°,
∴∠3=180° 90° ∠1=40°,
又∵要使得ab,
∴只需要∠2=∠3=40°,
故答案为:40.
16.2
【分析】根据平行线的判定定理(同位角相等,两直线平行)进行判断即可.
【解析】解:∵∠GHD=53°,
∵∠GHC=127°,
∵∠IGA=127°,
∴∠GHC=∠IGA,∠IGB=53°,
∴AB∥CD,
∵∠EFB=53°,
∴∠IGB=∠EFB,
∴IH∥EF.
故答案为:2.
17.3
【分析】本题主要考查两直线平行的判定,在复杂的图形中具有相等关系或互补关系的两角首先要判断它们是否是同位角、内错角或同旁内角,被判断平行的两直线是否由“三线八角”而产生的被截直线;
【解析】解:由题知:,则(同位角相等,两直线平行);
,则(内错角相等,两直线平行).
,则(同旁内角互补,两直线平行).
则线段、、、、、中,相互平行的线段有:,,共3组;
故答案为:3
18.①③④
【分析】根据对顶角相等、平行线的判定逐个判断即可得.
【解析】解:①,根据内错角相等,两直线平行可判断;
②,根据同位角相等,两直线平行可判断;
③,根据同旁内角互补,两直线平行可判断;
④,
,根据同旁内角互补,两直线平行可判断;
综上,能判断的是①③④,
故答案为:①③④.
三、解答题
19.
证明: ,(已知)
又,(对顶角相等)
.(等量代换)
.(同位角相等,两直线平行)
20.解:(1)由,根据“同位角相等,两直线平行”,可得;
(2)由,根据“内错角相等两直线平行”,可得;
(3)由,根据“同旁内角互补,两直线平行”,可得.
21.证明:证法1:如图, 与交于
( 对顶角相等 )
又( 已知 )
( 等量代换 )
( 同位角相等,两直线平行 )
证法2:如图,
( 对顶角相等 )
又( 已知 )
( 等量代换 )
( 内错角相等,两直线平行 )
证法3:如图,
( 邻补角互补 )
( 对顶角相等 )
又( 已知 )
( 等量代换 )
( 同旁内角相等,两直线平行 )
22.解:,证明如下:
,
,
,
,
.
23.证明:(已知),
∴(垂直的定义),
,
又∵与互余(已知),
∴
(同角的余角相等),
(已知),
(等量代换),
(内错角相等,两直线平行).
24.解:因为平分,平分(已知),
所以,(角平分线的定义),
因为(已知),
所以(等量代换),
因为(已知),
所以(等量代换),
所以(同位角相等,两直线平行).
故答案为:角平分线的定义;等量代换;已知;等量代换;同位角相等,两直线平行.
25.证明:∵∠1+∠2=180°(已知)
又∵∠1=∠AOE(对顶角相等)
∴∠AOE+∠2=180°
∴DE∥AC,(同旁内角互补,两直线平行)
∴∠C=∠DEB(两直线平行,同位角相等)
又∵∠C=∠D(已知)
∴∠D=∠DEB
∴AD∥BC(内错角相等两直线平行).
故答案为对顶角相等,∠AOE,AC,同旁内角互补,两直线平行,∠DEB,两直线平行,同位角相等,∠DEB,内错角相等两直线平行.
26.证明:∵平分(已知),
∴(角平分线的定义).
∵平分(已知),
∴(角平分线的定义).
∴(等量代换).
∵(已知),
∴(等量代换).
∴(同旁内角互补,两直线平行).
一、单选题
1.如图,直线,被第三条直线所截.由“”,得到“”的依据是( )
A.两直线平行,同位角相等 B.同位角相等,两直线平行
C.两直线平行,内错角相等 D.内错角相等,两直线平行
2.如图,下列条件中,能判定直线的是( )
A. B. C. D.
3.如图,已知,要使, 则需具备的另一个条件是( )
A. B. C. D.
4.如图所示,已知,那么下列结论正确的是( )
A. B. C. D.
5.如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.平行于同一条直线的两条直线平行
6.如图,下列推论正确的是( )
A., B.,
C., D.,
7.如图,下列条件:①,②,③,④,⑤,⑥中能判断直线的有( )
A.3个 B.4个 C.5个 D.6个
8.如图,木条、、通过、两处螺丝固定在一起,且,,将木条、木条、木条看作是在同一平面内的三条直线、、,若使直线、直线达到平行的位置关系,则下列描述正确的是( )
A.木条、固定不动,木条绕点顺时针旋转
B.木条、固定不动,木条绕点逆时针旋转
C.木条、固定不动,木条绕点逆时针旋转
D.木条、固定不动,木条绕点顺时针旋转
9.如图,下列条件中:①,②,③,④,能判断的有( )
A.1个 B.2个 C.3个 D.4个
10.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度可以是( )
A.第一次向右拐40°,第二次向左拐140° B.第一次向左拐40°,第二次向右拐40°
C.第一次向左拐40°,第二次向右拐140° D.第一次向右拐40°,第二次向右拐40°
二、填空题
11.如图,填空:
(1)若∠A=∠3,则____∥_____,理由是______;
(2)若∠2=∠E,则____∥___,理由是____;
(3)若∠A+∠ABE=180°,则____∥___,理由是____;
(4)若∠2=∠____,则DA∥EB,理由是____;
(5)若∠DBC+∠_____=180°,则DB∥EC,理由是____;
12.如图,已知直线被直线所截,交点分别为H、G,(请你添加一个合适的条件), ,则.
13.如图,两块三角板形状大小完全相同,则边的依据是 .(写一个即可)
14.如图,∠1=2x+10°,∠2=40°-x,当∠1= 度时,DE∥BC.
15.如图,把三角尺的直角顶点放在直线b上.若∠1= 50°,则当∠2= 时,ab.
16.如图,∠EFB=∠GHD=53°,∠IGA=127°,由这些条件,能找到 对平行线.
17.如图,将三个相同的三角尺不重叠不留空隙地拼在一起,则线段、、、、、中,相互平行的线段有 组.
18.如图,下列条件能判断的是 (多选).
① ② ③ ④
三、解答题
19.已知:如图, .求证: .
分析:如图,欲证,只要证______.
证明: ,(已知)
又,( )
__________.( )
.(__________,____________)
20.如图,是上一点,是上一点,是延长线上一点.
(1)如果,可以判断哪两条直线平行?为什么?
(2)如果,可以判断哪两条直线平行?为什么?
(3)如果,可以判断哪两条直线平行?为什么?
21.已知:如图,直线被所截, ,
求证: .
证法1:如图, 与交于
( )
又( )
( )
( )
证法2:如图,
( )
又( )
( )
( )
证法3:如图,
( )
( )
又( )
( )
( )
22.如图,已知,.判断与的位置关系,并证明.
23.已知:如图,,和互余,于点G,求证:.(推理过程请注明理由)
24.如图,已知,平分,平分,且,请填写说明DE∥BF的理由的依据.
解:因为平分,平分(已知)
所以,(______)
因为(已知)
所以(______)
因为(______)
所以(______)
所以DEBF(______)
25.如图,,求证:,请将证明过程填写完整.
证明:∵(已知)
又∵( )
∴________,
∴____________( )
∴______________( )
又∵(已知)
∴________________,
∴( )
26.完成下面的证明:
如图,平分,平分,且.
求证:.
证明:∵平分(已知),
∴( ).
又∵平分( ),
∴______( ).
( ).
又∵(已知),
(______)( ).
∴( ).
答案
一、单选题
1.D
【分析】本题考查了平行线的判定,熟练掌握内错角相等,两直线平行是解题的关键.
根据平行线的判定判断作答即可.
【解析】解:∵,
∴(内错角相等,两直线平行),
故选:D.
2.B
【分析】本题考查的是平行线的判定,熟知平行线的判定定理是解答此题的关键.根据平行线的判定定理对各小题进行逐一判断即可.
【解析】解:A.,不能判定,不符合题意;
B.,同位角相等,则,符合题意;
C.,不能判定,不符合题意;
D.,不能判定,不符合题意.
故选:B.
3.D
【分析】根据平行线的判定方法,求解即可.
【解析】解:∵
∴
当时,,,可得
故选:D
4.B
【分析】本题考查了平行线的判定,解答本题的关键是掌握平行线的判定定理:内错角相等,两直线平行.和是直线、被直线所截的内错角,若,则.
【解析】解:,
(内错角相等,两直线平行)
故选:B
5.B
【分析】本题考查平行线的判定,根据内错角相等,两直线平行,进行判断即可.
【解析】解:如图,由题意,得:,
∴(内错角相等,两直线平行);
故选B.
6.D
【分析】利用平行线的判定方法判断即可得到结果.
【解析】解:A、,
∴(内错角相等,两直线平行),不符合题意;
B、,
∴(同位角相等,两直线平行),不符合题意;
C、由无法得到,不符合题意;
D、,
∴(同位角相等,两直线平行),符合题意.
故选:D.
7.C
【分析】本题主要考查了平行线的判定.同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.依据平行线的判定方法即可得出结论.
【解析】解:①由,可得;
②由,可得;
③由,,可得,即可得到;
④由,不能得到;
⑤由,可得,即可得到;
⑥由,,可得,即可得到;
故选:C.
8.C
【分析】要使直线、直线达到平行的位置关系,则要使(二者是内错角)或(二者是同旁内角),据此逐一判断即可
【解析】解:A、木条、固定不动,木条绕点顺时针旋转,则此时,则与不平行,不符合题意;
B、木条、固定不动,木条绕点逆时针旋转, 则此时,即,则与不平行,不符合题意;
C、木条、固定不动,木条绕点逆时针旋转,则,则与平行,符合题意;
D、木条、固定不动,木条绕点顺时针旋转,则,即,则与不平行,符不合题意;
故选C.
9.C
【分析】由平行线的判定定理进行判断,即可得到答案.
【解析】解:,则;故①符合题意;
,则;故②不符合题意;
,则;故③符合题意;
由,,则,得;故④符合题意;
故选:C
10.B
【分析】两次拐弯后,行驶方向与原来相同,说明两次拐弯后的方向是平行的.对题中的四个选项提供的条件,运用平行线的判定进行判断,能判定两直线平行者即为正确答案.
【解析】A、如图1:∵∠1=40°,∠2=140°,
∴AB与CD不平行;
故本选项错误;
B、如图2:∵∠1=40°,∠2=40°,
∴∠1=∠2,
∴AB与CD平行;
故本选项正确;
C、如图3:∵∠1=40°,∠2=140°,
∴∠1≠∠2,
∴AB不平行CD;
故本选项错误;
D、如图4:∠1=40°,∠2=40°,
∴∠3=140°,
∴∠1≠∠3,
∴AB与CD不平行;
故本选项错误.
故选B.
二、填空题
11.
【解析】(1)若∠A=∠3,则_AD__∥__BE__,理由是;(同位角相等,两直线平行);
(2)若∠2=∠E,则__BD__∥_CE__,理由是(内错角相等,两直线平行);
(3)若∠A+∠ABE=180°,则_AD___∥__BE_,理由是(同旁内角互补,两直线平行);
(4)若∠2=∠_D___,则DA∥EB,理由是(内错角相等,两直线平行);
(5)若∠DBC+∠_C_=180°,则DB∥EC,理由是(同旁内角互补,两直线平行);
故答案为(1). AD (2). BE (3). 同位角相等,两直线平行; (4). BD, (5)CE, (6)内错角相等,两直线平行; (7). AD, (8)BE, (9)同旁内角互补,两直线平行; (10). D (11). 内错角相等,两直线平行; (12).C, (13) 同旁内角互补,两直线平行.
12.(答案不唯一)
【分析】本题考查平行线的判定,根据平行线的判定定理添加条件即可.
【解析】解:添加,根据“同位角相等,两直线平行”可得;
添加,根据“内错角相等,两直线平行”可得;
添加,根据“同旁内角互补,两直线平行”可得;
故答案为:(答案不唯一).
13.同位角相等,两直线平行(答案不唯一)
【分析】利用平行线的判定方法即可解决问题.
【解析】解:依题意,
∴(同位角相等,两直线平行)
故答案为:同位角相等,两直线平行(答案不唯一).
14.30
【分析】根据平行线的判定定理得出当∠1=∠2时,DE∥BC,推出方程2x+10=40-x,求出x的值,即可求出∠1.
【解析】当∠1=∠2时,DE∥BC,
即2x+10=40 x,
解得:x=10,
∠1=(2×10+10)度=30度,
故答案为30.
15.40°
【分析】根据三角尺的直角顶点在直线b上,∠1=50°,即可得到∠3=180° 90° ∠1=40°,再根据ab,即可得到∠2=∠3=40°.
【解析】解:如图,
∵三角尺的直角顶点在直线b上,∠1=20°,
∴∠3=180° 90° ∠1=40°,
又∵要使得ab,
∴只需要∠2=∠3=40°,
故答案为:40.
16.2
【分析】根据平行线的判定定理(同位角相等,两直线平行)进行判断即可.
【解析】解:∵∠GHD=53°,
∵∠GHC=127°,
∵∠IGA=127°,
∴∠GHC=∠IGA,∠IGB=53°,
∴AB∥CD,
∵∠EFB=53°,
∴∠IGB=∠EFB,
∴IH∥EF.
故答案为:2.
17.3
【分析】本题主要考查两直线平行的判定,在复杂的图形中具有相等关系或互补关系的两角首先要判断它们是否是同位角、内错角或同旁内角,被判断平行的两直线是否由“三线八角”而产生的被截直线;
【解析】解:由题知:,则(同位角相等,两直线平行);
,则(内错角相等,两直线平行).
,则(同旁内角互补,两直线平行).
则线段、、、、、中,相互平行的线段有:,,共3组;
故答案为:3
18.①③④
【分析】根据对顶角相等、平行线的判定逐个判断即可得.
【解析】解:①,根据内错角相等,两直线平行可判断;
②,根据同位角相等,两直线平行可判断;
③,根据同旁内角互补,两直线平行可判断;
④,
,根据同旁内角互补,两直线平行可判断;
综上,能判断的是①③④,
故答案为:①③④.
三、解答题
19.
证明: ,(已知)
又,(对顶角相等)
.(等量代换)
.(同位角相等,两直线平行)
20.解:(1)由,根据“同位角相等,两直线平行”,可得;
(2)由,根据“内错角相等两直线平行”,可得;
(3)由,根据“同旁内角互补,两直线平行”,可得.
21.证明:证法1:如图, 与交于
( 对顶角相等 )
又( 已知 )
( 等量代换 )
( 同位角相等,两直线平行 )
证法2:如图,
( 对顶角相等 )
又( 已知 )
( 等量代换 )
( 内错角相等,两直线平行 )
证法3:如图,
( 邻补角互补 )
( 对顶角相等 )
又( 已知 )
( 等量代换 )
( 同旁内角相等,两直线平行 )
22.解:,证明如下:
,
,
,
,
.
23.证明:(已知),
∴(垂直的定义),
,
又∵与互余(已知),
∴
(同角的余角相等),
(已知),
(等量代换),
(内错角相等,两直线平行).
24.解:因为平分,平分(已知),
所以,(角平分线的定义),
因为(已知),
所以(等量代换),
因为(已知),
所以(等量代换),
所以(同位角相等,两直线平行).
故答案为:角平分线的定义;等量代换;已知;等量代换;同位角相等,两直线平行.
25.证明:∵∠1+∠2=180°(已知)
又∵∠1=∠AOE(对顶角相等)
∴∠AOE+∠2=180°
∴DE∥AC,(同旁内角互补,两直线平行)
∴∠C=∠DEB(两直线平行,同位角相等)
又∵∠C=∠D(已知)
∴∠D=∠DEB
∴AD∥BC(内错角相等两直线平行).
故答案为对顶角相等,∠AOE,AC,同旁内角互补,两直线平行,∠DEB,两直线平行,同位角相等,∠DEB,内错角相等两直线平行.
26.证明:∵平分(已知),
∴(角平分线的定义).
∵平分(已知),
∴(角平分线的定义).
∴(等量代换).
∵(已知),
∴(等量代换).
∴(同旁内角互补,两直线平行).
同课章节目录
