(从课本到奥数)奥数专题第六讲:长方体和正方体(三)-数学五年级下册人教版
文档属性
| 名称 | (从课本到奥数)奥数专题第六讲:长方体和正方体(三)-数学五年级下册人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 561.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-02 00:00:00 | ||
图片预览




文档简介
第六讲 :长方体和正方体(三)
知识精讲
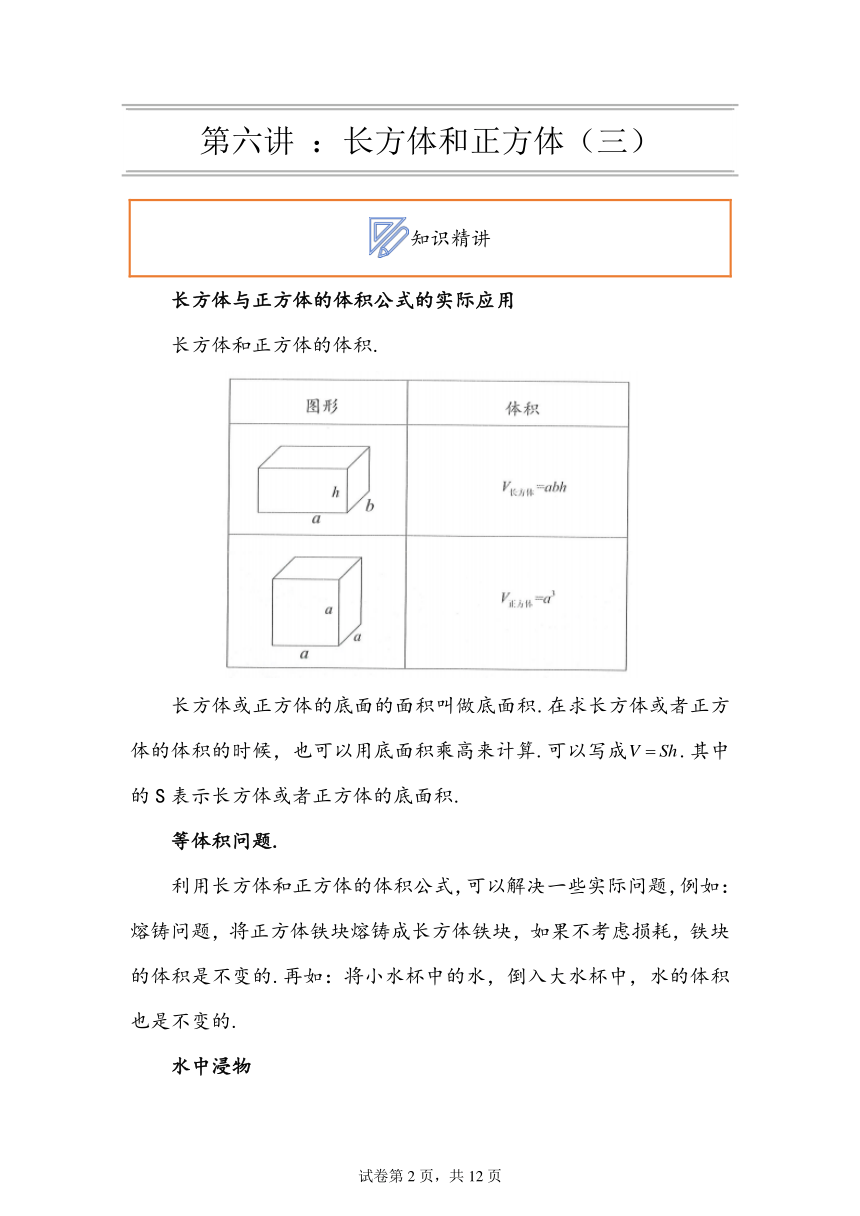
长方体与正方体的体积公式的实际应用
长方体和正方体的体积.
长方体或正方体的底面的面积叫做底面积.在求长方体或者正方体的体积的时候,也可以用底面积乘高来计算.可以写成.其中的S表示长方体或者正方体的底面积.
等体积问题.
利用长方体和正方体的体积公式,可以解决一些实际问题,例如:熔铸问题,将正方体铁块熔铸成长方体铁块,如果不考虑损耗,铁块的体积是不变的.再如:将小水杯中的水,倒入大水杯中,水的体积也是不变的.
水中浸物
前面已经学习过正方体和长方体的体积公式,但是有一些物体既不是正方体也不是长方体,它们的体积该如何进行计算呢
可以用排水法计算不规则物体的体积,例如称量一个铁球的体积,具体操作步骤如下:在一个容器内先装一定量的水,容器中的水要足够多,能够完全浸没被测物体,容器保证足够大,能够放下被测物体,并且浸没时水不会溢出.
首先先确定容器内水的体积,例如图1中烧杯内水的体积是300毫升,接下来将要称量的铁球浸没在水中,观察浸没后图2的水面高度对应的体积是500毫升,那么这个铁球的体积是(毫升).
求不规则物体的体积可以用排水法,物体的体积等于浸没在水中时水面上升的那部分的体积,即容器的底面积乘水面上升的高度.
题型汇总
题型一:长方体、正方体体积的实际应用
1.光明学校游泳池长40米,宽25米,深2米,要把游泳池四周及底面贴上瓷砖。
(1)一共需要贴多少平方米的瓷砖?
(2)为了学生的安全,游泳池的水位设定为1.2米,需要向水池注入多少立方米的水?
【答案】(1)1260平方米
(2)1200立方米
【分析】(1)贴瓷砖的面积=长×宽+长×高×2+宽×高×2,据此列式解答;
(2)水位相当于长方体的高,根据长方体体积=长×宽×高,求出注入的水的体积。
【详解】(1)40×25+40×2×2+25×2×2
=1000+160+100
=1260(平方米)
答:一共需要贴1260平方米的瓷砖。
(2)40×25×1.2=1200(立方米)
答:需要向水池注入1200立方米的水。
2.下图是一块长方体木料。从这块木料上锯下一个最大的正方体。
(1)正方体木料的体积是多少立方厘米?
(2)剩余部分的体积是多少立方厘米?
【答案】(1)1728立方厘米
(2)1152立方厘米
【分析】(1)长方体木料锯下最大的正方体,正方体的棱长=长方体最短的棱,根据正方体体积=棱长×棱长×棱长,列式解答即可;
(2)长方体体积=长×宽×高,长方体体积-正方体体积=剩余部分的体积,据此列式解答。
【详解】(1)12×12×12=1728(立方厘米)
答:正方体木料的体积是1728立方厘米。
(2)20×12×12-1728
=2880-1728
=1152(立方厘米)
答:剩余部分的体积是1152立方厘米。
题型二:等体积问题-熔铸
1.把一个棱长为0.8米的正方体实心铁块,煅铸成一块宽为0.8米,高为0.4米的长方体实心零件(不计损耗)。
(1)长方体零件的长应是多少米?
(2)这个长方体零件的表面积是多少?
【答案】(1)1.6米
(2)4.48平方米
【分析】(1)根据正方体的体积公式:V=,代入数据求出正方体铁块的体积,熔铸后,体积不变,再根据长方体的体积公式:V=abh,代入数据即可求出这个长方体铁块的长。
(2)根据长方体的表面积=(长×宽+宽×高+长×高)×2,代入数据解答即可。
【详解】(1)0.8×0.8×0.8=0.512(立方米)
0.512÷0.8÷0.4
=0.64÷0.4
=1.6(米)
答:长方体零件的长应是1.6米。
(2)(1.6×0.8+0.8×0.4+1.6×0.4)×2
=(1.28+0.32+0.64)×2
=(1.6+0.64)×2
=2.24×2
=4.48(平方米)
答:这个长方体零件的表面积是4.48平方米。
2.把一块长是3分米、宽是6厘米、高是9厘米的长方体铁块,锻造成边长是3厘米的小正方体铁块,能锻造成多少块?
【答案】60块
【分析】根据题意,3分米=30厘米,结合长方体的体积公式:长×高×宽,先求出长方体铁块的体积,再根据正方体的体积公式:边长×边长×边长,用长方体的体积除以正方体的体积,即可求出答案。
【详解】3分米=30厘米
30×6×9
=180×9
=1620(立方厘米)
3×3×3
=9×3
=27(立方厘米)
1620÷27=60(块)
答:能锻造成60块。
题型三:等体积问题-侧面竖起
1.有一个长方体容器(图1),长30厘米,宽20厘米,高10厘米,里面的水深6厘米。为了节约占地面积,把这个容器盖紧,再朝左竖起来(图2),里面的水深应该是多少?
【答案】18厘米
【分析】首先要明确无论容器怎么放,里面的水的体积不变,先根据“长方体的体积=长×宽×高”求出容器中水的体积。把容器朝左竖起来时,左侧面成为长方体的底面,根据“长方体的体积=底面积×高”,用水的体积除以左侧面面积(宽×高)即可求出这时的水深,如果让长10厘米、宽20厘米的面朝下,则这个面成为底面,同样用水的体积除以这个面的面积,即可求出这时水的深度。
【详解】30×20×6
=600×6
=3600(立方厘米)
3600÷(10×20)
=3600÷200
=18(厘米)
答:里面的水深应该是18厘米。
2.在一个封闭的水箱内装入水,从里面量,水箱的长、宽、高如下左图所示。水深24厘米,如果把这个水箱立起来放(如下右图),这时水深有多少厘米?
【答案】72厘米
【分析】根据长方体体积公式:体积=长×宽×高,代入数据,求出左图形里水深24厘米的水的体积,由于体积不变,再用水的体积÷(右图的长×宽),即可求出这时水深,据此解答。
【详解】90×60×24÷(60×30)
=90×60×24÷1800
=5400×24÷1800
=129600÷1800
=72(厘米)
答:这时水深72厘米。
题型四:水中浸物
1.在一个长80厘米、宽50厘米、高40厘米的长方体水箱中有30厘米深的水。如果在水中沉入一个棱长为20厘米的正方体铁块,这时水箱中水深多少厘米?
【答案】32厘米
【分析】将水中沉入一个棱长为20厘米的正方体铁块,则水面上升的体积就是正方体的体积,根据,得出水上升的体积,长方体的体积=底面积×高,长方体的底面积=长×宽,那么用水上升的体积除以长方体的底面积,就是水面上升的高度,最后再加上原来水箱中水的高度就是现在水的深度。
【详解】20×20×20=8000(立方厘米)
8000÷(80×50)
=8000÷4000
=2(厘米)
30+2=32(厘米)
答:这时水箱中水深32厘米。
2.数学实践活动课上,王老师带来了甲、乙两个容器(已知两个容器中装有同样多的水,甲容器里面长30厘米,宽20厘米;乙容器内水高21厘米),并布置了一项实验活动。
实验内容:利用提供的辅助工具测量甲、乙容器中水的体积。
辅助工具:一块小石头、一把断尺、一支笔。
小明思考片刻后做起了实验,并很快计算出了两个容器中水的体积。下面是小明的实验过程和实验数据:
同学们,你知道小明是怎样求出乙容器中水的体积的吗?请在答题卡上写出计算过程。
【答案】见详解
【分析】两个容器中,水面上升的体积就是小石头的体积,根据长方体体积=长×宽×高,甲容器的长×宽×水面上升的高度=小石头的体积,即乙容器水面上升的体积,乙容器水面上升的体积÷乙容器水面上升的高度=乙容器的底面积,再用乙容器的底面积×原来的高,即可求出水的体积。
【详解】30×20×2÷3=400(平方厘米)
400×21=8400(立方厘米)
答:乙容器中水的体积是8400立方厘米。
跟踪训练
一、选择题
1.如图,在一个长方体玻璃容器里摆了若干个棱长为1厘米的小正方体,这个玻璃容器的容积是( )立方厘米。
A.72 B.75 C.90 D.108
2.一个长方体水箱,从里面量长5分米,宽4分米,高3分米,箱中水面高2分米,把一个棱长2分米的正方体铁块放入水箱,水面会上升多少分米?( )
A.0.4分米 B.0.8分米 C.1.2分米 D.1.4分米
3.长方体的长,宽,高都扩大到原来的3倍,那么它的体积会扩大到原来的( )倍。
A.6 B.9 C.27 D.3
4.把64升水倒入一个长4分米,宽2.5分米,高8分米的长方体水箱中,这时水面距箱口多少分米?( )
A.6.4 B.3.2 C.0.6 D.1.6
5.把一个棱长是8厘米的正方体钢锭,熔铸成一个长方体钢锭,已知长方体的长是5厘米,宽是8厘米,它的高是( )厘米。
A.12.6 B.12 C.9.6 D.12.8
二、填空题
6.一个长方体,长、宽、高分别为5m、1m和2m,如果把这个长方体平放在地面上,占地面积最大是( )m2,最小是( )m2,这个长方体的体积是( )m3。
7.要在平地上挖一个长20米、宽8米、深50厘米的长方体土坑,一共要挖出( )方的土,土坑占地面积是( )平方厘米。
8.一个棱长5厘米的正方体玻璃水箱,里面装有3厘米深的水,当把一块不规则的石头完全浸入水中后,水面上升到4厘米,这块石头的体积是( )立方厘米。
9.将一个棱长总和是60厘米的正方体实心铁块锻造成一个长是10厘米,宽是2厘米的长方体实心铁块,这个长方体铁块的高是( )厘米。
10.小丽有一个封闭的长方体容器(如下图),长4分米,宽1分米,高2分米,里面水深16厘米。现在她把这个容器的左侧面平放于桌面上。这时水深( )分米。
三、解答题
11.一根方钢的长是3米,它的横断面是一个边长为2分米的正方形。已知1立方分米的钢重7.8千克,这根方钢重多少千克?
12.一个正方体铁块,棱长是4分米。把它锻造成长和宽分别是5分米、4分米的长方体,锻造成的长方体铁块的高是多少分米?(消耗的部分忽略不计)
13.一个长方体的体积是125立方厘米,底面积是25平方厘米。这个长方体的高是多少厘米?
14.如图。如果长方体水箱的底面积是16平方分米,那么石块的体积是多少立方分米?
15.在学过排水法测量体积之后,红红想测量家中一个土豆的体积。她拿出一个可封闭的长方体玻璃缸,并注入水,如下左图所示。可这时水面高度只有3厘米,放入土豆后无法淹没土豆。红红灵机一动,扣好盖子把玻璃缸立了起来,如下右图。请求出这个土豆的体积。
16.有甲、乙两个长方体容器,从甲容器内部量得长、宽、高分别为40厘米、10厘米、10厘米。将甲容器的右面作为底面,直立起来就是乙容器,已知甲容器中装有水,将其倾斜,水面刚好如下图所示。乙容器是空的。
(1)甲容器中水的体积是多少?
(2)现在把甲、乙两个容器放在同一桌面上,将甲容器中的水倒一部分到乙容器中,使得甲、乙容器中的水面一样高,那么乙容器中需要倒入多少毫升水?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
【分析】通过平移图形可知,这个长方体容器的里面的长是6厘米,宽是5厘米,高是3厘米,根据长方体的容积公式:,把数据代入公式解答。
【详解】
(立方厘米)
所以,这个玻璃容器的容积是90立方厘米。
故答案为:C
2.A
【分析】水箱中的水面高度=正方体铁块棱长,将正方体铁块放入水箱,铁块完全浸入水中,水面上升的体积就是铁块的体积,根据正方体棱长=棱长×棱长×棱长,求出水面上升的体积,再根据长方体的高=体积÷底面积,即可求出水面上升的高度。
【详解】2×2×2÷(5×4)
=8÷20
=0.4(分米)
水面会上升0.4分米。
故答案为:A
3.C
【分析】根据长方体的体积=长×宽×高,原来长方体的体积=长×宽×高,扩大后的长方体的体积=长×3×宽×3×高×3,因此现在的体积会扩大到原来(3×3×3)倍,据此解答。
【详解】3×3×3=27
因此它的体积会扩大到原来的27倍。
故答案为:C
4.D
【分析】水倒入长方体后,体积不变,变成一个长4分米,宽2.5分米的长方体,先求出64升水在长4分米,宽2.5分米,高8分米的长方体水箱中的高度,该高度=水的体积÷长方体水箱的底面积,再用水箱的高度减去水的高度即可。
【详解】64升=64立方分米
64÷(4×2.5)
=64÷10
=6.4(分米)
8-6.4=1.6(分米)
这时水面距箱口1.6分米。
故答案为:D
5.D
【分析】根据题意,正方体的钢锭的体积等于长方体钢锭的体积,根据得出正方体的体积是512立方厘米,即长方体的体积也是512立方厘米,根据,得出长方体的高=体积÷长÷宽。
【详解】8×8×8=512(平方厘米)
512÷5÷8=12.8(厘米)
它的高是12.8厘米。
故答案为:D
6. 10 2 10
【分析】根据题意可知:这个长方体的最大面的面积=长×高,最小面的面积=宽×高,据此求出占地面积最大和最小的情况;长方体的体积=长×宽×高,把数据代入公式解答即可。
【详解】5×2=10(m2)
1×2=2(m2)
5×1×2
=5×2
=10(m3)
一个长方体,长、宽、高分别为5m、1m和2m,如果把这个长方体平放在地面上,占地面积最大是10m2,最小是2m2,这个长方体的体积是10m3。
7. 80 1600000
【分析】第一问就是要求长方体的体积,根据1方=1立方米,先把50厘米转化为0.5米,再根据,代入数据计算后把单位转化为方即可。
第二问就是要求长方体的底面积,土坑占地面积是一个长是20米,宽是8米的长方形,根据长方形的面积=长×宽,代入数据计算,再根据1平方米=10000平方厘米,把单位转化为平方厘米即可。
【详解】50厘米=0.5米
(立方米)=80(方)
(平方米)=1600000(平方厘米)
要在平地上挖一个长20米、宽8米、深50厘米的长方体土坑,一共要挖出80方的土,土坑占地面积是1600000平方厘米。
8.25
【分析】这块石头的体积=上升的水的体积。根据题意,上升的水的形状是长5厘米,宽5厘米,高(4-3)厘米的长方体,根据长方体的体积=长×宽×高,代入数据计算即可求出这块石头的体积。
【详解】5×5×(4-3)
=5×5×1
=25(立方厘米)
则这块石头的体积是25立方厘米。
9.6.25
【分析】已知正方体实心铁块的棱长总和是60厘米,根据正方体的棱长=棱长总和÷12,求出正方体铁块的棱长;再根据正方体的体积公式V=a3,求出铁块的体积。
已知把这块正方体实心铁块锻造成一个长方体实心铁块,铁块的体积不变;根据长方体的高=体积÷长÷宽,求出长方体铁块的高。
【详解】60÷12=5(厘米)
5×5×5=125(立方厘米)
125÷10÷2
=12.5÷2
=6.25(厘米)
这个长方体铁块的高是6.25厘米。
10.3.2
【分析】长方体容器中水的形状是长4分米,宽1分米,深16厘米(即1.6分米)的长方体,根据长方体的体积=长×宽×高,代入数据计算,可以求出容器中水的体积。把这个容器的左侧面平放于桌面上,水的体积不变,这时长是2分米,宽是1分米,用求得的水的体积连续除以2和1,即可求出水深的高度。
【详解】16厘米=1.6分米
4×1×1.6÷2÷1
=6.4÷2÷1
=3.2(分米)
则这时水深3.2分米。
11.936千克
【分析】根据长方体体积公式:体积=长×宽×高,根据题意可知,方钢的长是2分米,宽是2分米,高是3米,根据1米=10分米,将单位统一,再代入数据,求出方钢的体积,再用方钢的体积乘7.8,即可求出方钢的重量。
【详解】3米=30分米
2×2×30×7.8
=120×7.8
=936(千克)
答:这根方钢重936千克。
12.3.2分米
【分析】由题意得,正方体变成长方体体积不变,可用正方体棱长求出正方体体积,正方体体积即是长方体体积。再用长乘宽求出长方体底面积,最后用体积除以底面积即可求出高。据此解答。
【详解】43÷(5×4)
=64÷(5×4)
=64÷20
=3.2(分米)
答:锻造成的长方体铁块的高是3.2分米。
13.5厘米
【分析】根据长方体的高=体积÷底面积,列式解答即可。
【详解】125÷25=5(厘米)
答:这个长方体的高是5厘米。
14.11.2立方分米
【分析】据题意可知,石块的体积等于上升的水的体积,用水箱的底面积乘上升的水的高度,即可得解。
【详解】
(立方分米)
答:石块的体积是11.2立方分米。
15.600立方厘米
【分析】先分析左图情况:左图中玻璃缸长30厘米,宽10厘米,水面高度3厘米。根据长方体体积公式:长方体体积=长×宽×高,此时水的体积为30×10×3=900(立方厘米);
再分析右图情况:右图中玻璃缸长10厘米,宽10厘米,水面高度15厘米。此时水和土豆的总体积为10×10×15=1500(立方厘米);
最后求土豆体积:用右图中水和土豆的总体积减去左图中水的体积,即土豆的体积为1500-900=600(立方厘米)
【详解】计算左图水的体积:
V1=30×10×3
=300×3
=900(立方厘米)
计算右图水和土豆总体积:
V2=10×10×15
=100×15
=1500(立方厘米)
土豆体积:V=V1-V2=1500-900=600(立方厘米)
这个土豆的体积为600立方厘米。
16.(1)2000立方厘米
(2)400毫升
【分析】(1)从图中可以看出,甲容器装水的体积等于甲容器体积的一半,根据长方体的体积公式V=abh,代入数据计算求解。
(2)从图中可知,甲容器的底面积是(40×10)平方厘米;将甲容器的右面作为底面,直立起来就是乙容器,则乙容器的底面积是(10×10)平方厘米;
将甲容器中的水倒一部分到乙容器中,使得甲、乙容器中的水面一样高,则水的体积不变,水的高度一样,那么可以把甲、乙两个容器看作一个底面积为甲、乙两个底面积之和的容器;
根据长方体的高h=V÷S,代入数据计算求出容器中水的高度;再根据长方体的体积公式V=abh,求出乙容器中水的体积。注意单位的换算:1立方厘米=1毫升。
【详解】(1)40×10×10÷2
=400×10÷2
=4000÷2
=2000(立方厘米)
答:甲容器中水的体积是2000立方厘米。
(2)2000÷(40×10+10×10)
=2000÷(400+100)
=2000÷500
=4(厘米)
10×10×4
=100×4
=400(立方厘米)
400立方厘米=400毫升
答:乙容器中需要倒入400毫升水。
答案第1页,共2页
答案第1页,共2页
知识精讲
长方体与正方体的体积公式的实际应用
长方体和正方体的体积.
长方体或正方体的底面的面积叫做底面积.在求长方体或者正方体的体积的时候,也可以用底面积乘高来计算.可以写成.其中的S表示长方体或者正方体的底面积.
等体积问题.
利用长方体和正方体的体积公式,可以解决一些实际问题,例如:熔铸问题,将正方体铁块熔铸成长方体铁块,如果不考虑损耗,铁块的体积是不变的.再如:将小水杯中的水,倒入大水杯中,水的体积也是不变的.
水中浸物
前面已经学习过正方体和长方体的体积公式,但是有一些物体既不是正方体也不是长方体,它们的体积该如何进行计算呢
可以用排水法计算不规则物体的体积,例如称量一个铁球的体积,具体操作步骤如下:在一个容器内先装一定量的水,容器中的水要足够多,能够完全浸没被测物体,容器保证足够大,能够放下被测物体,并且浸没时水不会溢出.
首先先确定容器内水的体积,例如图1中烧杯内水的体积是300毫升,接下来将要称量的铁球浸没在水中,观察浸没后图2的水面高度对应的体积是500毫升,那么这个铁球的体积是(毫升).
求不规则物体的体积可以用排水法,物体的体积等于浸没在水中时水面上升的那部分的体积,即容器的底面积乘水面上升的高度.
题型汇总
题型一:长方体、正方体体积的实际应用
1.光明学校游泳池长40米,宽25米,深2米,要把游泳池四周及底面贴上瓷砖。
(1)一共需要贴多少平方米的瓷砖?
(2)为了学生的安全,游泳池的水位设定为1.2米,需要向水池注入多少立方米的水?
【答案】(1)1260平方米
(2)1200立方米
【分析】(1)贴瓷砖的面积=长×宽+长×高×2+宽×高×2,据此列式解答;
(2)水位相当于长方体的高,根据长方体体积=长×宽×高,求出注入的水的体积。
【详解】(1)40×25+40×2×2+25×2×2
=1000+160+100
=1260(平方米)
答:一共需要贴1260平方米的瓷砖。
(2)40×25×1.2=1200(立方米)
答:需要向水池注入1200立方米的水。
2.下图是一块长方体木料。从这块木料上锯下一个最大的正方体。
(1)正方体木料的体积是多少立方厘米?
(2)剩余部分的体积是多少立方厘米?
【答案】(1)1728立方厘米
(2)1152立方厘米
【分析】(1)长方体木料锯下最大的正方体,正方体的棱长=长方体最短的棱,根据正方体体积=棱长×棱长×棱长,列式解答即可;
(2)长方体体积=长×宽×高,长方体体积-正方体体积=剩余部分的体积,据此列式解答。
【详解】(1)12×12×12=1728(立方厘米)
答:正方体木料的体积是1728立方厘米。
(2)20×12×12-1728
=2880-1728
=1152(立方厘米)
答:剩余部分的体积是1152立方厘米。
题型二:等体积问题-熔铸
1.把一个棱长为0.8米的正方体实心铁块,煅铸成一块宽为0.8米,高为0.4米的长方体实心零件(不计损耗)。
(1)长方体零件的长应是多少米?
(2)这个长方体零件的表面积是多少?
【答案】(1)1.6米
(2)4.48平方米
【分析】(1)根据正方体的体积公式:V=,代入数据求出正方体铁块的体积,熔铸后,体积不变,再根据长方体的体积公式:V=abh,代入数据即可求出这个长方体铁块的长。
(2)根据长方体的表面积=(长×宽+宽×高+长×高)×2,代入数据解答即可。
【详解】(1)0.8×0.8×0.8=0.512(立方米)
0.512÷0.8÷0.4
=0.64÷0.4
=1.6(米)
答:长方体零件的长应是1.6米。
(2)(1.6×0.8+0.8×0.4+1.6×0.4)×2
=(1.28+0.32+0.64)×2
=(1.6+0.64)×2
=2.24×2
=4.48(平方米)
答:这个长方体零件的表面积是4.48平方米。
2.把一块长是3分米、宽是6厘米、高是9厘米的长方体铁块,锻造成边长是3厘米的小正方体铁块,能锻造成多少块?
【答案】60块
【分析】根据题意,3分米=30厘米,结合长方体的体积公式:长×高×宽,先求出长方体铁块的体积,再根据正方体的体积公式:边长×边长×边长,用长方体的体积除以正方体的体积,即可求出答案。
【详解】3分米=30厘米
30×6×9
=180×9
=1620(立方厘米)
3×3×3
=9×3
=27(立方厘米)
1620÷27=60(块)
答:能锻造成60块。
题型三:等体积问题-侧面竖起
1.有一个长方体容器(图1),长30厘米,宽20厘米,高10厘米,里面的水深6厘米。为了节约占地面积,把这个容器盖紧,再朝左竖起来(图2),里面的水深应该是多少?
【答案】18厘米
【分析】首先要明确无论容器怎么放,里面的水的体积不变,先根据“长方体的体积=长×宽×高”求出容器中水的体积。把容器朝左竖起来时,左侧面成为长方体的底面,根据“长方体的体积=底面积×高”,用水的体积除以左侧面面积(宽×高)即可求出这时的水深,如果让长10厘米、宽20厘米的面朝下,则这个面成为底面,同样用水的体积除以这个面的面积,即可求出这时水的深度。
【详解】30×20×6
=600×6
=3600(立方厘米)
3600÷(10×20)
=3600÷200
=18(厘米)
答:里面的水深应该是18厘米。
2.在一个封闭的水箱内装入水,从里面量,水箱的长、宽、高如下左图所示。水深24厘米,如果把这个水箱立起来放(如下右图),这时水深有多少厘米?
【答案】72厘米
【分析】根据长方体体积公式:体积=长×宽×高,代入数据,求出左图形里水深24厘米的水的体积,由于体积不变,再用水的体积÷(右图的长×宽),即可求出这时水深,据此解答。
【详解】90×60×24÷(60×30)
=90×60×24÷1800
=5400×24÷1800
=129600÷1800
=72(厘米)
答:这时水深72厘米。
题型四:水中浸物
1.在一个长80厘米、宽50厘米、高40厘米的长方体水箱中有30厘米深的水。如果在水中沉入一个棱长为20厘米的正方体铁块,这时水箱中水深多少厘米?
【答案】32厘米
【分析】将水中沉入一个棱长为20厘米的正方体铁块,则水面上升的体积就是正方体的体积,根据,得出水上升的体积,长方体的体积=底面积×高,长方体的底面积=长×宽,那么用水上升的体积除以长方体的底面积,就是水面上升的高度,最后再加上原来水箱中水的高度就是现在水的深度。
【详解】20×20×20=8000(立方厘米)
8000÷(80×50)
=8000÷4000
=2(厘米)
30+2=32(厘米)
答:这时水箱中水深32厘米。
2.数学实践活动课上,王老师带来了甲、乙两个容器(已知两个容器中装有同样多的水,甲容器里面长30厘米,宽20厘米;乙容器内水高21厘米),并布置了一项实验活动。
实验内容:利用提供的辅助工具测量甲、乙容器中水的体积。
辅助工具:一块小石头、一把断尺、一支笔。
小明思考片刻后做起了实验,并很快计算出了两个容器中水的体积。下面是小明的实验过程和实验数据:
同学们,你知道小明是怎样求出乙容器中水的体积的吗?请在答题卡上写出计算过程。
【答案】见详解
【分析】两个容器中,水面上升的体积就是小石头的体积,根据长方体体积=长×宽×高,甲容器的长×宽×水面上升的高度=小石头的体积,即乙容器水面上升的体积,乙容器水面上升的体积÷乙容器水面上升的高度=乙容器的底面积,再用乙容器的底面积×原来的高,即可求出水的体积。
【详解】30×20×2÷3=400(平方厘米)
400×21=8400(立方厘米)
答:乙容器中水的体积是8400立方厘米。
跟踪训练
一、选择题
1.如图,在一个长方体玻璃容器里摆了若干个棱长为1厘米的小正方体,这个玻璃容器的容积是( )立方厘米。
A.72 B.75 C.90 D.108
2.一个长方体水箱,从里面量长5分米,宽4分米,高3分米,箱中水面高2分米,把一个棱长2分米的正方体铁块放入水箱,水面会上升多少分米?( )
A.0.4分米 B.0.8分米 C.1.2分米 D.1.4分米
3.长方体的长,宽,高都扩大到原来的3倍,那么它的体积会扩大到原来的( )倍。
A.6 B.9 C.27 D.3
4.把64升水倒入一个长4分米,宽2.5分米,高8分米的长方体水箱中,这时水面距箱口多少分米?( )
A.6.4 B.3.2 C.0.6 D.1.6
5.把一个棱长是8厘米的正方体钢锭,熔铸成一个长方体钢锭,已知长方体的长是5厘米,宽是8厘米,它的高是( )厘米。
A.12.6 B.12 C.9.6 D.12.8
二、填空题
6.一个长方体,长、宽、高分别为5m、1m和2m,如果把这个长方体平放在地面上,占地面积最大是( )m2,最小是( )m2,这个长方体的体积是( )m3。
7.要在平地上挖一个长20米、宽8米、深50厘米的长方体土坑,一共要挖出( )方的土,土坑占地面积是( )平方厘米。
8.一个棱长5厘米的正方体玻璃水箱,里面装有3厘米深的水,当把一块不规则的石头完全浸入水中后,水面上升到4厘米,这块石头的体积是( )立方厘米。
9.将一个棱长总和是60厘米的正方体实心铁块锻造成一个长是10厘米,宽是2厘米的长方体实心铁块,这个长方体铁块的高是( )厘米。
10.小丽有一个封闭的长方体容器(如下图),长4分米,宽1分米,高2分米,里面水深16厘米。现在她把这个容器的左侧面平放于桌面上。这时水深( )分米。
三、解答题
11.一根方钢的长是3米,它的横断面是一个边长为2分米的正方形。已知1立方分米的钢重7.8千克,这根方钢重多少千克?
12.一个正方体铁块,棱长是4分米。把它锻造成长和宽分别是5分米、4分米的长方体,锻造成的长方体铁块的高是多少分米?(消耗的部分忽略不计)
13.一个长方体的体积是125立方厘米,底面积是25平方厘米。这个长方体的高是多少厘米?
14.如图。如果长方体水箱的底面积是16平方分米,那么石块的体积是多少立方分米?
15.在学过排水法测量体积之后,红红想测量家中一个土豆的体积。她拿出一个可封闭的长方体玻璃缸,并注入水,如下左图所示。可这时水面高度只有3厘米,放入土豆后无法淹没土豆。红红灵机一动,扣好盖子把玻璃缸立了起来,如下右图。请求出这个土豆的体积。
16.有甲、乙两个长方体容器,从甲容器内部量得长、宽、高分别为40厘米、10厘米、10厘米。将甲容器的右面作为底面,直立起来就是乙容器,已知甲容器中装有水,将其倾斜,水面刚好如下图所示。乙容器是空的。
(1)甲容器中水的体积是多少?
(2)现在把甲、乙两个容器放在同一桌面上,将甲容器中的水倒一部分到乙容器中,使得甲、乙容器中的水面一样高,那么乙容器中需要倒入多少毫升水?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
【分析】通过平移图形可知,这个长方体容器的里面的长是6厘米,宽是5厘米,高是3厘米,根据长方体的容积公式:,把数据代入公式解答。
【详解】
(立方厘米)
所以,这个玻璃容器的容积是90立方厘米。
故答案为:C
2.A
【分析】水箱中的水面高度=正方体铁块棱长,将正方体铁块放入水箱,铁块完全浸入水中,水面上升的体积就是铁块的体积,根据正方体棱长=棱长×棱长×棱长,求出水面上升的体积,再根据长方体的高=体积÷底面积,即可求出水面上升的高度。
【详解】2×2×2÷(5×4)
=8÷20
=0.4(分米)
水面会上升0.4分米。
故答案为:A
3.C
【分析】根据长方体的体积=长×宽×高,原来长方体的体积=长×宽×高,扩大后的长方体的体积=长×3×宽×3×高×3,因此现在的体积会扩大到原来(3×3×3)倍,据此解答。
【详解】3×3×3=27
因此它的体积会扩大到原来的27倍。
故答案为:C
4.D
【分析】水倒入长方体后,体积不变,变成一个长4分米,宽2.5分米的长方体,先求出64升水在长4分米,宽2.5分米,高8分米的长方体水箱中的高度,该高度=水的体积÷长方体水箱的底面积,再用水箱的高度减去水的高度即可。
【详解】64升=64立方分米
64÷(4×2.5)
=64÷10
=6.4(分米)
8-6.4=1.6(分米)
这时水面距箱口1.6分米。
故答案为:D
5.D
【分析】根据题意,正方体的钢锭的体积等于长方体钢锭的体积,根据得出正方体的体积是512立方厘米,即长方体的体积也是512立方厘米,根据,得出长方体的高=体积÷长÷宽。
【详解】8×8×8=512(平方厘米)
512÷5÷8=12.8(厘米)
它的高是12.8厘米。
故答案为:D
6. 10 2 10
【分析】根据题意可知:这个长方体的最大面的面积=长×高,最小面的面积=宽×高,据此求出占地面积最大和最小的情况;长方体的体积=长×宽×高,把数据代入公式解答即可。
【详解】5×2=10(m2)
1×2=2(m2)
5×1×2
=5×2
=10(m3)
一个长方体,长、宽、高分别为5m、1m和2m,如果把这个长方体平放在地面上,占地面积最大是10m2,最小是2m2,这个长方体的体积是10m3。
7. 80 1600000
【分析】第一问就是要求长方体的体积,根据1方=1立方米,先把50厘米转化为0.5米,再根据,代入数据计算后把单位转化为方即可。
第二问就是要求长方体的底面积,土坑占地面积是一个长是20米,宽是8米的长方形,根据长方形的面积=长×宽,代入数据计算,再根据1平方米=10000平方厘米,把单位转化为平方厘米即可。
【详解】50厘米=0.5米
(立方米)=80(方)
(平方米)=1600000(平方厘米)
要在平地上挖一个长20米、宽8米、深50厘米的长方体土坑,一共要挖出80方的土,土坑占地面积是1600000平方厘米。
8.25
【分析】这块石头的体积=上升的水的体积。根据题意,上升的水的形状是长5厘米,宽5厘米,高(4-3)厘米的长方体,根据长方体的体积=长×宽×高,代入数据计算即可求出这块石头的体积。
【详解】5×5×(4-3)
=5×5×1
=25(立方厘米)
则这块石头的体积是25立方厘米。
9.6.25
【分析】已知正方体实心铁块的棱长总和是60厘米,根据正方体的棱长=棱长总和÷12,求出正方体铁块的棱长;再根据正方体的体积公式V=a3,求出铁块的体积。
已知把这块正方体实心铁块锻造成一个长方体实心铁块,铁块的体积不变;根据长方体的高=体积÷长÷宽,求出长方体铁块的高。
【详解】60÷12=5(厘米)
5×5×5=125(立方厘米)
125÷10÷2
=12.5÷2
=6.25(厘米)
这个长方体铁块的高是6.25厘米。
10.3.2
【分析】长方体容器中水的形状是长4分米,宽1分米,深16厘米(即1.6分米)的长方体,根据长方体的体积=长×宽×高,代入数据计算,可以求出容器中水的体积。把这个容器的左侧面平放于桌面上,水的体积不变,这时长是2分米,宽是1分米,用求得的水的体积连续除以2和1,即可求出水深的高度。
【详解】16厘米=1.6分米
4×1×1.6÷2÷1
=6.4÷2÷1
=3.2(分米)
则这时水深3.2分米。
11.936千克
【分析】根据长方体体积公式:体积=长×宽×高,根据题意可知,方钢的长是2分米,宽是2分米,高是3米,根据1米=10分米,将单位统一,再代入数据,求出方钢的体积,再用方钢的体积乘7.8,即可求出方钢的重量。
【详解】3米=30分米
2×2×30×7.8
=120×7.8
=936(千克)
答:这根方钢重936千克。
12.3.2分米
【分析】由题意得,正方体变成长方体体积不变,可用正方体棱长求出正方体体积,正方体体积即是长方体体积。再用长乘宽求出长方体底面积,最后用体积除以底面积即可求出高。据此解答。
【详解】43÷(5×4)
=64÷(5×4)
=64÷20
=3.2(分米)
答:锻造成的长方体铁块的高是3.2分米。
13.5厘米
【分析】根据长方体的高=体积÷底面积,列式解答即可。
【详解】125÷25=5(厘米)
答:这个长方体的高是5厘米。
14.11.2立方分米
【分析】据题意可知,石块的体积等于上升的水的体积,用水箱的底面积乘上升的水的高度,即可得解。
【详解】
(立方分米)
答:石块的体积是11.2立方分米。
15.600立方厘米
【分析】先分析左图情况:左图中玻璃缸长30厘米,宽10厘米,水面高度3厘米。根据长方体体积公式:长方体体积=长×宽×高,此时水的体积为30×10×3=900(立方厘米);
再分析右图情况:右图中玻璃缸长10厘米,宽10厘米,水面高度15厘米。此时水和土豆的总体积为10×10×15=1500(立方厘米);
最后求土豆体积:用右图中水和土豆的总体积减去左图中水的体积,即土豆的体积为1500-900=600(立方厘米)
【详解】计算左图水的体积:
V1=30×10×3
=300×3
=900(立方厘米)
计算右图水和土豆总体积:
V2=10×10×15
=100×15
=1500(立方厘米)
土豆体积:V=V1-V2=1500-900=600(立方厘米)
这个土豆的体积为600立方厘米。
16.(1)2000立方厘米
(2)400毫升
【分析】(1)从图中可以看出,甲容器装水的体积等于甲容器体积的一半,根据长方体的体积公式V=abh,代入数据计算求解。
(2)从图中可知,甲容器的底面积是(40×10)平方厘米;将甲容器的右面作为底面,直立起来就是乙容器,则乙容器的底面积是(10×10)平方厘米;
将甲容器中的水倒一部分到乙容器中,使得甲、乙容器中的水面一样高,则水的体积不变,水的高度一样,那么可以把甲、乙两个容器看作一个底面积为甲、乙两个底面积之和的容器;
根据长方体的高h=V÷S,代入数据计算求出容器中水的高度;再根据长方体的体积公式V=abh,求出乙容器中水的体积。注意单位的换算:1立方厘米=1毫升。
【详解】(1)40×10×10÷2
=400×10÷2
=4000÷2
=2000(立方厘米)
答:甲容器中水的体积是2000立方厘米。
(2)2000÷(40×10+10×10)
=2000÷(400+100)
=2000÷500
=4(厘米)
10×10×4
=100×4
=400(立方厘米)
400立方厘米=400毫升
答:乙容器中需要倒入400毫升水。
答案第1页,共2页
答案第1页,共2页
同课章节目录
