【课堂无忧】人教版四下5.7《四边形的内角和》(课件)
文档属性
| 名称 | 【课堂无忧】人教版四下5.7《四边形的内角和》(课件) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 16:35:11 | ||
图片预览




文档简介
(共44张PPT)
5.7
四边形的内角和
(人教版)四年级
下
01
教学目标
02
新知导入
03
任务一
04
任务二
05
拓展延伸
06
课堂练习
07
课堂小结
08
作业布置
09
板书设计
01
教学目标
通过测量、剪拼、观察等活动探究四边形的内角和,能运用四边形的内角和为360°这一规律解决一些实际问题。
01
02
经历观察、思考、推理、归纳的过程,培养学生的探究推理能力、发现能力、观察和动手操作能力。
03
在各种活动中体验探索的乐趣和成功的快乐,培养合作探究精神,掌握一些学习与研究的方法。
02
新知导入
三角形
小
提
示
三角形的内角和是180°。
02
新知导入
从三角形上剪下一个小的三角形,剩下的变成了什么图形?
变成一个四边形了。
02
新知导入
看到四边形,你想知道什么?
我想知道四边形的内角和是多少度?
学习任务一
阅读与理解
03
任务一
四边形的内角和是多少度?
读一读这句话,你觉得哪些词语比较关键?
四边形和内角和。
四边形内角和是指一个四边形内部四个内角的角度之和。
03
任务一
可以画锐角三角形、也可以画直角三角形,还可以画钝角三角形。
学习任务:
请同学们在练习本上画一个自己喜欢的三角形。
四边形的内角和是多少度?
03
任务一
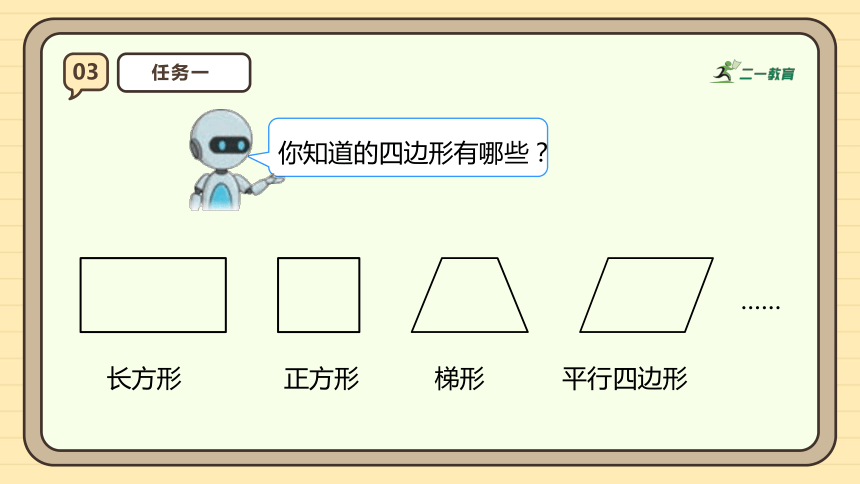
你知道的四边形有哪些?
长方形
正方形
梯形
平行四边形
……
03
任务一
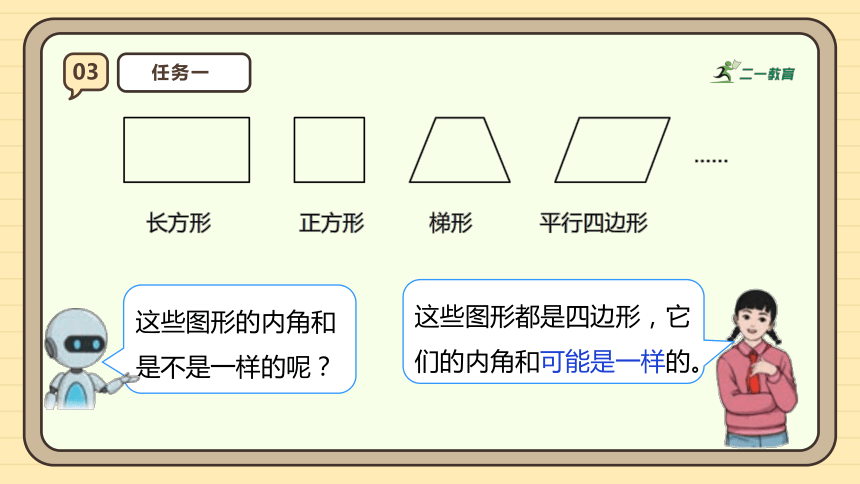
这些图形都是四边形,它们的内角和可能是一样的。
这些图形的内角和是不是一样的呢?
学习任务二
分析与解答
04
任务二
在这些四边形中,你能直接求出哪些四边形的内角?
04
任务二
观察长方形和正方形这类特殊的四边形,它们的内角和是多少度?
长方形和正方形的4个角都是直角,它们的内角和是360°。
04
任务二
小
提
示
长方形、正方形这两个特殊的四边形的内角和是360°。
是不是所有的四边形内角和都是360度?
你有什么样的猜测?
04
任务二
从特殊的情况入手,提出自己的猜测,是一种很好的解决问题的方法。但从特殊情况得出的结论是否具有一般性,还需要我们进行验证。
04
任务二
大家回忆一下,我们在研究三角形的内角和时用到了哪些方法?
65°+70°+45°=180°
测量法,把三角形三个角的度数量出来,然后相加。
04
任务二
大家回忆一下,我们在研究三角形的内角和时用到了哪些方法?
剪拼法,把三角形的三个内角剪下来,再拼一拼,看看能拼成什么角。
04
任务二
65°+70°+45°=180°
测量法
剪拼法
这两种方法你觉得哪种方法更准确、更严谨呢?
剪拼的方法更准确,因为测量中有误差。
04
任务二
小
提
示
测量中难免有误差,所以我们在探究中应该选择更准确、更严谨的方法。
分组探究求出其他四边形的内角和的方法。
04
任务二
小组合作:
1.拿出准备好的四边形,选择你喜欢的方法求出四边形的内角和。
2.小组内交流讨论,得出结论:四边形的内角和是( )。
04
任务二
用什么办法求出其他四边形的内角和?
拼成的图形刚好是一个周角。
小
提
示
四边形的内角和是360°。
04
任务二
用什么办法求出其他四边形的内角和?
把四边形分成两个三角形。
一个三角形的内角和是180°
2个三角形的内角和加起来就是360°
四边形的内角和是360°
180°+180°= 360°
04
任务二
你怎么知道四边形的内角和就等于这两个三角形的内角和呢?
两个三角形的所有内角正好是四边形的四个内角。
学习任务三
回顾与反思
05
任务三
思考:
我们已经知道了这些四边形的内角和是360°,那么其它形状的四边形的内角和还是360°吗?
05
任务三
它们的内角和还是360°。
因为它们都可以分成两个三角形。
其它形状的四边形的内角和还是360°吗?
05
任务三
……
任何一个四边形,只要从一个顶点出发,连接与它不相邻的顶点,都可以将它分割成两个三角形。
05
任务三
我们大家共同证明了所有四边形的内角和都是360°。
答:四边形的内角和是360度。
四边形的内角和是多少度?
05
任务三
结合前面所学的知识,你们想一想,最好最直接的办法是怎样的?
四边形被分成了两个三角形,它的内角和就含有两个180°。
06
课堂练习
基础题:
1.判断。
√
×
一个四边形有三个内角是 90°,这个四边形一定是正方形。
06
课堂练习
基础题:
1.判断。
√
×
一个四边形的内角和是360°,把它平均分成4个小三角形,每个小三角形的内角和就是90°。
06
课堂练习
基础题:
2.你能想办法求出下边这个多边形的内角和吗?
180°×3=540°
答:这个多边形的内角和是540°。
06
作业设计
提高题:
3.如图四边形ABCD沿AO、BO、CO、DO剪开,,得到4个三角形,这4个三角形的内角和与原四边形的内角和相比有什么变化?
180°×4=720°
720°-360°=360°
答:比原四边形的内角和多360度。
A
B
C
D
O
06
作业设计
拓展题:
4.正方形切去一角后,所得多边形的内角和为多少度?在下图中试一试。
180°×3=540°
180°
360°
【知识技能类作业】
必做题:
1.判断。
(1)四边形越大,它的内角和越大。 ( )
(2)把一个平行四边形剪成一个梯形,内角和变小了。 ( )
(3)任意一个四边形的内角和是任意一个三角形的内角和的2倍。
( )
(4)任意四边形的内角和是360度。 ( )
07
作业设计
×
×
√
√
07
作业设计
【知识技能类作业】
必做题:
2.算出下面图形的内角和。
180°×6=1080°
答:这个多边形的内角和是1080°。
07
课堂练习
【知识技能类作业】
选做题:
1.选一选。
(1)四边形ABCD中,如果∠A+∠C+∠D=280°,则∠B的度数是( )。
A.80° B.90° C.170° D.20°
(2) 在四边形的内角中,锐角的个数不能多于( )。
A.2个 B.3个 C.4个 D.5个
A
B
07
作业设计
【知识技能类作业】
选做题:
2.四边形的四个内角可以都是锐角吗?可以都是钝角吗?可以都是直角吗?为什么?
不可以都是锐角,应为锐角是大于零度小于九十度,都是锐角则内角和必定小于360度;
也不能都是钝角都是钝角则内角和必定大于360度;
可以都是直角,内角和等于360度刚好满足四边形内角和等于360度。
08
课堂小结
通过今天的学习,你有哪些收获?
我知道了所有四边形的内角和都是360°。
我通过转化思想研究出了多边形的内角和。
09
作业布置
【综合实践类作业】
人们用各种形状的地砖铺路,调查请地砖的形状,尝试算出一块地砖的内角和。
10
板书设计
四边形的内角和
所有四边形的内角和都是360°。
180°+180°= 360°
https://www.21cnjy.com/recruitment/home/fine
5.7
四边形的内角和
(人教版)四年级
下
01
教学目标
02
新知导入
03
任务一
04
任务二
05
拓展延伸
06
课堂练习
07
课堂小结
08
作业布置
09
板书设计
01
教学目标
通过测量、剪拼、观察等活动探究四边形的内角和,能运用四边形的内角和为360°这一规律解决一些实际问题。
01
02
经历观察、思考、推理、归纳的过程,培养学生的探究推理能力、发现能力、观察和动手操作能力。
03
在各种活动中体验探索的乐趣和成功的快乐,培养合作探究精神,掌握一些学习与研究的方法。
02
新知导入
三角形
小
提
示
三角形的内角和是180°。
02
新知导入
从三角形上剪下一个小的三角形,剩下的变成了什么图形?
变成一个四边形了。
02
新知导入
看到四边形,你想知道什么?
我想知道四边形的内角和是多少度?
学习任务一
阅读与理解
03
任务一
四边形的内角和是多少度?
读一读这句话,你觉得哪些词语比较关键?
四边形和内角和。
四边形内角和是指一个四边形内部四个内角的角度之和。
03
任务一
可以画锐角三角形、也可以画直角三角形,还可以画钝角三角形。
学习任务:
请同学们在练习本上画一个自己喜欢的三角形。
四边形的内角和是多少度?
03
任务一
你知道的四边形有哪些?
长方形
正方形
梯形
平行四边形
……
03
任务一
这些图形都是四边形,它们的内角和可能是一样的。
这些图形的内角和是不是一样的呢?
学习任务二
分析与解答
04
任务二
在这些四边形中,你能直接求出哪些四边形的内角?
04
任务二
观察长方形和正方形这类特殊的四边形,它们的内角和是多少度?
长方形和正方形的4个角都是直角,它们的内角和是360°。
04
任务二
小
提
示
长方形、正方形这两个特殊的四边形的内角和是360°。
是不是所有的四边形内角和都是360度?
你有什么样的猜测?
04
任务二
从特殊的情况入手,提出自己的猜测,是一种很好的解决问题的方法。但从特殊情况得出的结论是否具有一般性,还需要我们进行验证。
04
任务二
大家回忆一下,我们在研究三角形的内角和时用到了哪些方法?
65°+70°+45°=180°
测量法,把三角形三个角的度数量出来,然后相加。
04
任务二
大家回忆一下,我们在研究三角形的内角和时用到了哪些方法?
剪拼法,把三角形的三个内角剪下来,再拼一拼,看看能拼成什么角。
04
任务二
65°+70°+45°=180°
测量法
剪拼法
这两种方法你觉得哪种方法更准确、更严谨呢?
剪拼的方法更准确,因为测量中有误差。
04
任务二
小
提
示
测量中难免有误差,所以我们在探究中应该选择更准确、更严谨的方法。
分组探究求出其他四边形的内角和的方法。
04
任务二
小组合作:
1.拿出准备好的四边形,选择你喜欢的方法求出四边形的内角和。
2.小组内交流讨论,得出结论:四边形的内角和是( )。
04
任务二
用什么办法求出其他四边形的内角和?
拼成的图形刚好是一个周角。
小
提
示
四边形的内角和是360°。
04
任务二
用什么办法求出其他四边形的内角和?
把四边形分成两个三角形。
一个三角形的内角和是180°
2个三角形的内角和加起来就是360°
四边形的内角和是360°
180°+180°= 360°
04
任务二
你怎么知道四边形的内角和就等于这两个三角形的内角和呢?
两个三角形的所有内角正好是四边形的四个内角。
学习任务三
回顾与反思
05
任务三
思考:
我们已经知道了这些四边形的内角和是360°,那么其它形状的四边形的内角和还是360°吗?
05
任务三
它们的内角和还是360°。
因为它们都可以分成两个三角形。
其它形状的四边形的内角和还是360°吗?
05
任务三
……
任何一个四边形,只要从一个顶点出发,连接与它不相邻的顶点,都可以将它分割成两个三角形。
05
任务三
我们大家共同证明了所有四边形的内角和都是360°。
答:四边形的内角和是360度。
四边形的内角和是多少度?
05
任务三
结合前面所学的知识,你们想一想,最好最直接的办法是怎样的?
四边形被分成了两个三角形,它的内角和就含有两个180°。
06
课堂练习
基础题:
1.判断。
√
×
一个四边形有三个内角是 90°,这个四边形一定是正方形。
06
课堂练习
基础题:
1.判断。
√
×
一个四边形的内角和是360°,把它平均分成4个小三角形,每个小三角形的内角和就是90°。
06
课堂练习
基础题:
2.你能想办法求出下边这个多边形的内角和吗?
180°×3=540°
答:这个多边形的内角和是540°。
06
作业设计
提高题:
3.如图四边形ABCD沿AO、BO、CO、DO剪开,,得到4个三角形,这4个三角形的内角和与原四边形的内角和相比有什么变化?
180°×4=720°
720°-360°=360°
答:比原四边形的内角和多360度。
A
B
C
D
O
06
作业设计
拓展题:
4.正方形切去一角后,所得多边形的内角和为多少度?在下图中试一试。
180°×3=540°
180°
360°
【知识技能类作业】
必做题:
1.判断。
(1)四边形越大,它的内角和越大。 ( )
(2)把一个平行四边形剪成一个梯形,内角和变小了。 ( )
(3)任意一个四边形的内角和是任意一个三角形的内角和的2倍。
( )
(4)任意四边形的内角和是360度。 ( )
07
作业设计
×
×
√
√
07
作业设计
【知识技能类作业】
必做题:
2.算出下面图形的内角和。
180°×6=1080°
答:这个多边形的内角和是1080°。
07
课堂练习
【知识技能类作业】
选做题:
1.选一选。
(1)四边形ABCD中,如果∠A+∠C+∠D=280°,则∠B的度数是( )。
A.80° B.90° C.170° D.20°
(2) 在四边形的内角中,锐角的个数不能多于( )。
A.2个 B.3个 C.4个 D.5个
A
B
07
作业设计
【知识技能类作业】
选做题:
2.四边形的四个内角可以都是锐角吗?可以都是钝角吗?可以都是直角吗?为什么?
不可以都是锐角,应为锐角是大于零度小于九十度,都是锐角则内角和必定小于360度;
也不能都是钝角都是钝角则内角和必定大于360度;
可以都是直角,内角和等于360度刚好满足四边形内角和等于360度。
08
课堂小结
通过今天的学习,你有哪些收获?
我知道了所有四边形的内角和都是360°。
我通过转化思想研究出了多边形的内角和。
09
作业布置
【综合实践类作业】
人们用各种形状的地砖铺路,调查请地砖的形状,尝试算出一块地砖的内角和。
10
板书设计
四边形的内角和
所有四边形的内角和都是360°。
180°+180°= 360°
https://www.21cnjy.com/recruitment/home/fine
