六年级数学下册人教版第三章第1.3节《圆柱的体积》课时练习(含答案)
文档属性
| 名称 | 六年级数学下册人教版第三章第1.3节《圆柱的体积》课时练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 748.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-02 00:00:00 | ||
图片预览



文档简介
六年级数学下册人教版第三章第1.3节《圆柱的体积》课时练习
一、填空题
1.一个长方形的长是20cm ,宽是10cm,以长为轴旋转一周,得到一个圆柱。它的体积是 dm3。
2.一个长方形铁皮如图所示,图中涂色部分刚好能做成一个油桶(接头处忽略不计),这个油桶的容积是 L。
3.已知圆柱和圆锥等高,且圆柱的底面半径与圆锥的底面半径的比是3:4,则圆柱与圆锥底面周长的比是 ,体积的比是 。
4.自来水管的内直径是2cm,水管内水的流速是每秒8cm。一名同学去洗手,走时忘记关水龙头,5分钟后另一名同学发现并关掉了水龙头,共浪费了 L水。
5.一个圆柱形保温杯,从外面量高是20cm,直径是8cm;从里面量高是18cm,直径是6cm。这个保温杯最多能装 mL水。
6.如图,一个容器由圆柱和圆锥两部分组成,圆柱和圆锥的高分别为20cm ,9cm。容器中装有一定量的水,若将容器倒置,使圆锥体处于正上方,则此时水面的高度为 cm。
7.如图,酒瓶中装有一些酒,倒进一个酒杯中,酒杯口的直径是酒瓶瓶身直径的一半,这瓶酒能倒满这种酒杯 杯。
8.有大小两种玻璃球,放入装有同样多水的圆柱形容器中(如图)。
(1)大玻璃球的体积是 cm3。
(2)大玻璃球与小玻璃球的体积之比是 。
(3)图④中水的高度是 cm。
二、判断题
9.只要两个圆柱的底面周长相等,它们的体积就一定相等。 ( )
10.一个圆柱与圆锥等底等高,圆柱的体积比圆锥多18m3,圆锥的体积是9m3。( )
11.用一张长方形的硬纸板分别横着和竖着卷成两个圆柱,这两个圆柱的体积一样大。( )
12.一个圆柱的高缩小到原来的,底面半径扩大到原来的3倍,它的体积不变。( )
13.如果圆柱体积是圆锥体积的3倍,那么它们一定是等底等高。( )
14.底面积和高分别相等的长方体和圆柱体体积不一定相等。( )
三、单选题
15.如图,把一个体积是 360 cm3 的圆柱形木料削成一个陀螺,陀螺的体积是( )cm3。
A.122 B.180 C.240 D.300
16.如果一个圆锥和一个圆柱的底面积相等,圆柱的高是圆锥的2倍,那么圆锥的体积是圆柱体积的( )。
A. B. C. D.
17.一个圆柱的底面半径扩大到原来的3倍,高扩大到原来的2倍,则体积扩大到原来的( )倍。
A.6 B.9 C.18 D.12
18.等底等高的圆柱、正方体和长方体的体积相比较,( )。
A.正方体的体积大 B.长方体的体积大
C.圆柱体的体积大 D.一样大
19.如图,圆柱形容器的底面半径为10cm,水的高度为12 cm,水中浸没着一个底面半径为4 cm的圆锥形铅锤,把铅锤从水中取出后,水面下降了0.7 cm。根据以上信息,不能解决的问题是( )。(容器的厚度忽略不计)
A.容器内装了多少水 B.铅锤的体积是多少
C.铅锤的高是多少 D.容器的高是多少
20.把一个底面直径是4d m、高是3dm的圆柱形容器注满水,现将一个底面积是高是50cm的圆柱形铁块竖直放入水中,溢出的水的体积是( )mL。
A.3 B.18 C.1800 D.3000
四、计算题
21.计算下面各圆柱的体积。
(1)
(2)
五、解决问题
22.为防止铁质零件生锈,需将零件浸入防锈油。现将一个底面是边长 10 cm 的正方形,高是12 cm 的长方体铁质零件放入一个底面直径20cm、高20cm 的圆柱形容器浸防锈油,那么容器内至少需要注入多少升防锈油才能将零件浸没?
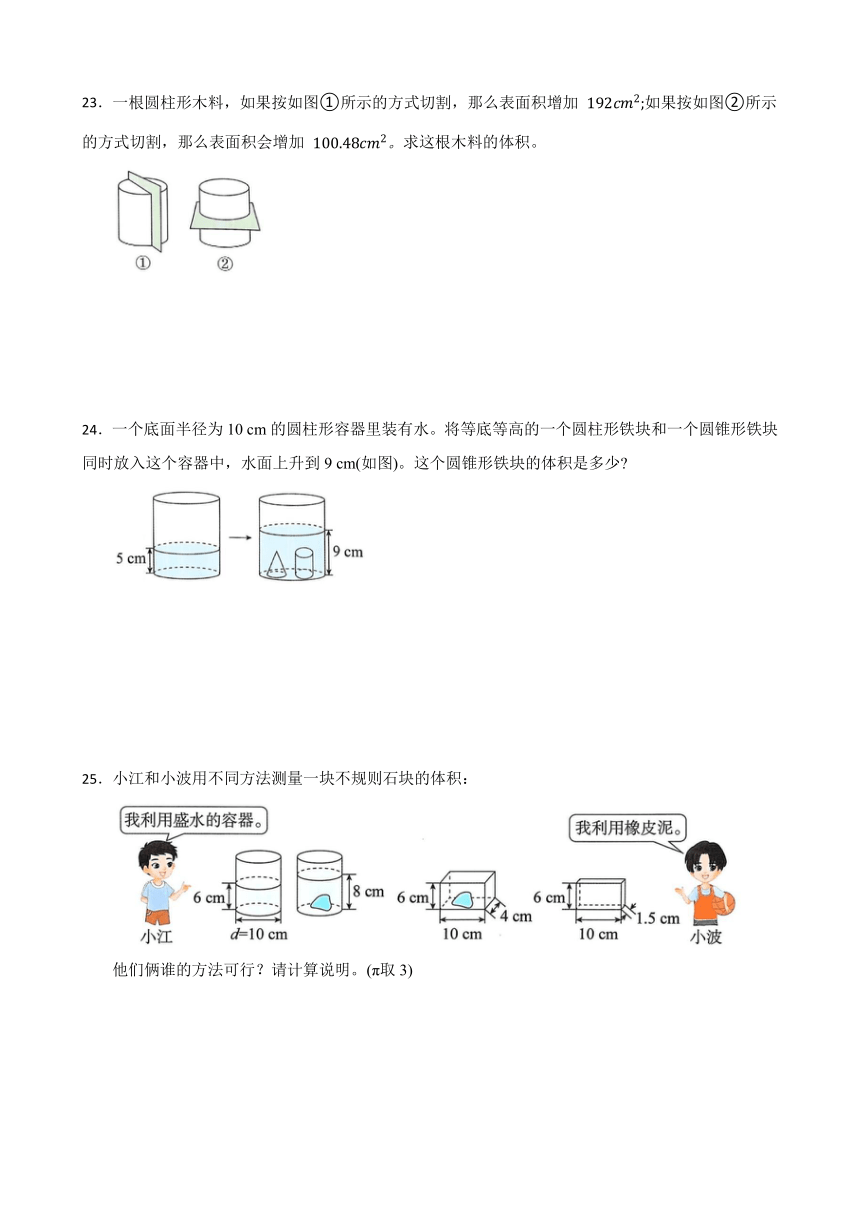
23.一根圆柱形木料,如果按如图①所示的方式切割,那么表面积增加 如果按如图②所示的方式切割,那么表面积会增加 求这根木料的体积。
24.一个底面半径为10 cm的圆柱形容器里装有水。将等底等高的一个圆柱形铁块和一个圆锥形铁块同时放入这个容器中,水面上升到9 cm(如图)。这个圆锥形铁块的体积是多少
25.小江和小波用不同方法测量一块不规则石块的体积:
他们俩谁的方法可行?请计算说明。(π取3)
26.积木是一种常见的儿童玩具,一套积木中通常有不同的颜色和形状。其中圆锥形积木是在圆柱形积木的基础上加工制作而成的。将一个底面半径是3c m、高是6 cm的圆柱形积木加工制作成一个等底等高的圆锥形积木,加工制作过程中削去的木料的体积是多少立方厘米
27.古希腊著名数学家阿基米德的墓碑上刻着一个“圆柱容球”的几何图形。如图,把一个球正好放在一个圆柱形容器中,球的直径、圆柱的高和底面直径均相等,此时球的体积正好是圆柱体积的。请你提出一个与圆柱有关的问题并解答。
答案
1.6.28
2.12.56
3.3:4;27:16
4.7.536
5.508.68
6.5
7.20
8.(1)100.48
(2)4:1
(3)8.5
9.错误
10.正确
11.错误
12.错误
13.错误
14.错误
15.C
16.B
17.C
18.D
19.D
20.C
21.(1)解:
(2)解:
22.解:3.14×(20÷2)2×10-10×10×12
=3.14×1000-1200
=3140-1200
=1940(cm3)
1940cm3=1940mL=1.94L
答:容器内至少需要注入1.94L防锈油才能将零件浸没。
23.解:100.48÷2÷3.14
=50.24÷3.14
=16(平方厘米)
16=4×4
192÷2÷(4×2)
=96÷8
=12(厘米)
3.14×42×12
=50.24×12
=602.88(立方厘米)
答:这根木料的体积为602.88cm3。
24.解:3.14×102×(9-5)
=314×4
=1256(立方厘米)
1256÷4=314(立方厘米)
答:这个圆锥形铁块的体积是314 cm3。
25.解:小江:
小波:10×4×6-10×1.5×6
=40×6-10×9
=240-90
=150(cm3)
答:他们俩的方法都可行,不规则石块的体积为150 cm3。
26.解:
答:加工制作过程中削去的木料的体积是113.04 cm3。
27.问题:当圆柱的高是3m 时,球的体积是多少立方米?
解答:
答:当圆柱的高是3m 时,球的体积是14.13 m3。
一、填空题
1.一个长方形的长是20cm ,宽是10cm,以长为轴旋转一周,得到一个圆柱。它的体积是 dm3。
2.一个长方形铁皮如图所示,图中涂色部分刚好能做成一个油桶(接头处忽略不计),这个油桶的容积是 L。
3.已知圆柱和圆锥等高,且圆柱的底面半径与圆锥的底面半径的比是3:4,则圆柱与圆锥底面周长的比是 ,体积的比是 。
4.自来水管的内直径是2cm,水管内水的流速是每秒8cm。一名同学去洗手,走时忘记关水龙头,5分钟后另一名同学发现并关掉了水龙头,共浪费了 L水。
5.一个圆柱形保温杯,从外面量高是20cm,直径是8cm;从里面量高是18cm,直径是6cm。这个保温杯最多能装 mL水。
6.如图,一个容器由圆柱和圆锥两部分组成,圆柱和圆锥的高分别为20cm ,9cm。容器中装有一定量的水,若将容器倒置,使圆锥体处于正上方,则此时水面的高度为 cm。
7.如图,酒瓶中装有一些酒,倒进一个酒杯中,酒杯口的直径是酒瓶瓶身直径的一半,这瓶酒能倒满这种酒杯 杯。
8.有大小两种玻璃球,放入装有同样多水的圆柱形容器中(如图)。
(1)大玻璃球的体积是 cm3。
(2)大玻璃球与小玻璃球的体积之比是 。
(3)图④中水的高度是 cm。
二、判断题
9.只要两个圆柱的底面周长相等,它们的体积就一定相等。 ( )
10.一个圆柱与圆锥等底等高,圆柱的体积比圆锥多18m3,圆锥的体积是9m3。( )
11.用一张长方形的硬纸板分别横着和竖着卷成两个圆柱,这两个圆柱的体积一样大。( )
12.一个圆柱的高缩小到原来的,底面半径扩大到原来的3倍,它的体积不变。( )
13.如果圆柱体积是圆锥体积的3倍,那么它们一定是等底等高。( )
14.底面积和高分别相等的长方体和圆柱体体积不一定相等。( )
三、单选题
15.如图,把一个体积是 360 cm3 的圆柱形木料削成一个陀螺,陀螺的体积是( )cm3。
A.122 B.180 C.240 D.300
16.如果一个圆锥和一个圆柱的底面积相等,圆柱的高是圆锥的2倍,那么圆锥的体积是圆柱体积的( )。
A. B. C. D.
17.一个圆柱的底面半径扩大到原来的3倍,高扩大到原来的2倍,则体积扩大到原来的( )倍。
A.6 B.9 C.18 D.12
18.等底等高的圆柱、正方体和长方体的体积相比较,( )。
A.正方体的体积大 B.长方体的体积大
C.圆柱体的体积大 D.一样大
19.如图,圆柱形容器的底面半径为10cm,水的高度为12 cm,水中浸没着一个底面半径为4 cm的圆锥形铅锤,把铅锤从水中取出后,水面下降了0.7 cm。根据以上信息,不能解决的问题是( )。(容器的厚度忽略不计)
A.容器内装了多少水 B.铅锤的体积是多少
C.铅锤的高是多少 D.容器的高是多少
20.把一个底面直径是4d m、高是3dm的圆柱形容器注满水,现将一个底面积是高是50cm的圆柱形铁块竖直放入水中,溢出的水的体积是( )mL。
A.3 B.18 C.1800 D.3000
四、计算题
21.计算下面各圆柱的体积。
(1)
(2)
五、解决问题
22.为防止铁质零件生锈,需将零件浸入防锈油。现将一个底面是边长 10 cm 的正方形,高是12 cm 的长方体铁质零件放入一个底面直径20cm、高20cm 的圆柱形容器浸防锈油,那么容器内至少需要注入多少升防锈油才能将零件浸没?
23.一根圆柱形木料,如果按如图①所示的方式切割,那么表面积增加 如果按如图②所示的方式切割,那么表面积会增加 求这根木料的体积。
24.一个底面半径为10 cm的圆柱形容器里装有水。将等底等高的一个圆柱形铁块和一个圆锥形铁块同时放入这个容器中,水面上升到9 cm(如图)。这个圆锥形铁块的体积是多少
25.小江和小波用不同方法测量一块不规则石块的体积:
他们俩谁的方法可行?请计算说明。(π取3)
26.积木是一种常见的儿童玩具,一套积木中通常有不同的颜色和形状。其中圆锥形积木是在圆柱形积木的基础上加工制作而成的。将一个底面半径是3c m、高是6 cm的圆柱形积木加工制作成一个等底等高的圆锥形积木,加工制作过程中削去的木料的体积是多少立方厘米
27.古希腊著名数学家阿基米德的墓碑上刻着一个“圆柱容球”的几何图形。如图,把一个球正好放在一个圆柱形容器中,球的直径、圆柱的高和底面直径均相等,此时球的体积正好是圆柱体积的。请你提出一个与圆柱有关的问题并解答。
答案
1.6.28
2.12.56
3.3:4;27:16
4.7.536
5.508.68
6.5
7.20
8.(1)100.48
(2)4:1
(3)8.5
9.错误
10.正确
11.错误
12.错误
13.错误
14.错误
15.C
16.B
17.C
18.D
19.D
20.C
21.(1)解:
(2)解:
22.解:3.14×(20÷2)2×10-10×10×12
=3.14×1000-1200
=3140-1200
=1940(cm3)
1940cm3=1940mL=1.94L
答:容器内至少需要注入1.94L防锈油才能将零件浸没。
23.解:100.48÷2÷3.14
=50.24÷3.14
=16(平方厘米)
16=4×4
192÷2÷(4×2)
=96÷8
=12(厘米)
3.14×42×12
=50.24×12
=602.88(立方厘米)
答:这根木料的体积为602.88cm3。
24.解:3.14×102×(9-5)
=314×4
=1256(立方厘米)
1256÷4=314(立方厘米)
答:这个圆锥形铁块的体积是314 cm3。
25.解:小江:
小波:10×4×6-10×1.5×6
=40×6-10×9
=240-90
=150(cm3)
答:他们俩的方法都可行,不规则石块的体积为150 cm3。
26.解:
答:加工制作过程中削去的木料的体积是113.04 cm3。
27.问题:当圆柱的高是3m 时,球的体积是多少立方米?
解答:
答:当圆柱的高是3m 时,球的体积是14.13 m3。
