7.3 二元一次方程组的应用 同步练习(含解析)
文档属性
| 名称 | 7.3 二元一次方程组的应用 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 816.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-03 05:52:35 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
7.3二元一次方程组的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某市出租车起步价所包含的路程为,超过的部分按每千米另收费.明明乘坐这种出租车走了,付了16元;盼盼乘坐这种出租车走了,付了28元.设这种出租车的起步价为元,超过后每千米收费元,则下列方程正确的是( )
A. B.
C. D.
2.已知关于x,y的二元一次方程组的解满足,则m的值为( )
A.0 B.1 C.2 D.3
3.台大收割机和台小收割机同时工作h共收割水稻,台大收割机和台小收割机同时工作h共收割水稻,设台大收割机和台小收割机每小时收割水稻分别是公顷、公顷,则下列列式正确的是( )
A. B.
C. D.
4.张三经营了一家草场,草场里面种植上等草和下等草.他卖五捆上等草的根数减去11根,就等于七捆下等草的根数;卖七捆上等草的根数减去25根,就等于五捆下等草的根数.设上等草一捆为根,下等草一捆为根,则下列方程正确的是( )
A. B. C. D.
5.一个两位数,十位数字比个位数字的2倍大1.若这个两位数减去36恰好等于个位数字与十位数字对调后所得的两位数,则这个两位数是( )
A.86 B.68 C.94 D.73
6.《九章算术》中记载“今有共买羊,人出五,不足四十五:人出七,则余三, 问人数、羊价各几何 ”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还多3钱, 问合伙人数、羊价各是多少?此问题中羊价为( )
A.150钱 B.155 钱 C.160钱 D.165钱
7.若方程组的解也是方程的解,则k的值为( )
A.7 B. C.10 D.15
8.在3月12日是植树节这天,小刚和小敏积极踊跃地参加植树活动,小刚平均每小时比小敏多植1棵树,小刚植树3小时,小敏植树2小时,两人一共植树18棵树.设小刚平均每小时植树x棵,小敏平均每小时植树y棵,那么根据题意,下列所列方程组中,正确的是( )
A. B.
C. D.
9.已知关于x、y的方程组,则下列结论中正确的是( )
①当a=1时,方程组的解也是方程x+y=2的解;②当x=y时,a=;③不论a取什么实数,2x+y的值始终不变.
A.①② B.①②③ C.②③ D.②
10.在明朝程大位《算法统宗》中有首住店诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗的大意是:一些客人到李三公的店中住宿,如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.设该店有客房x间,房客y人,则可列方程组为( )
A. B.
C. D.
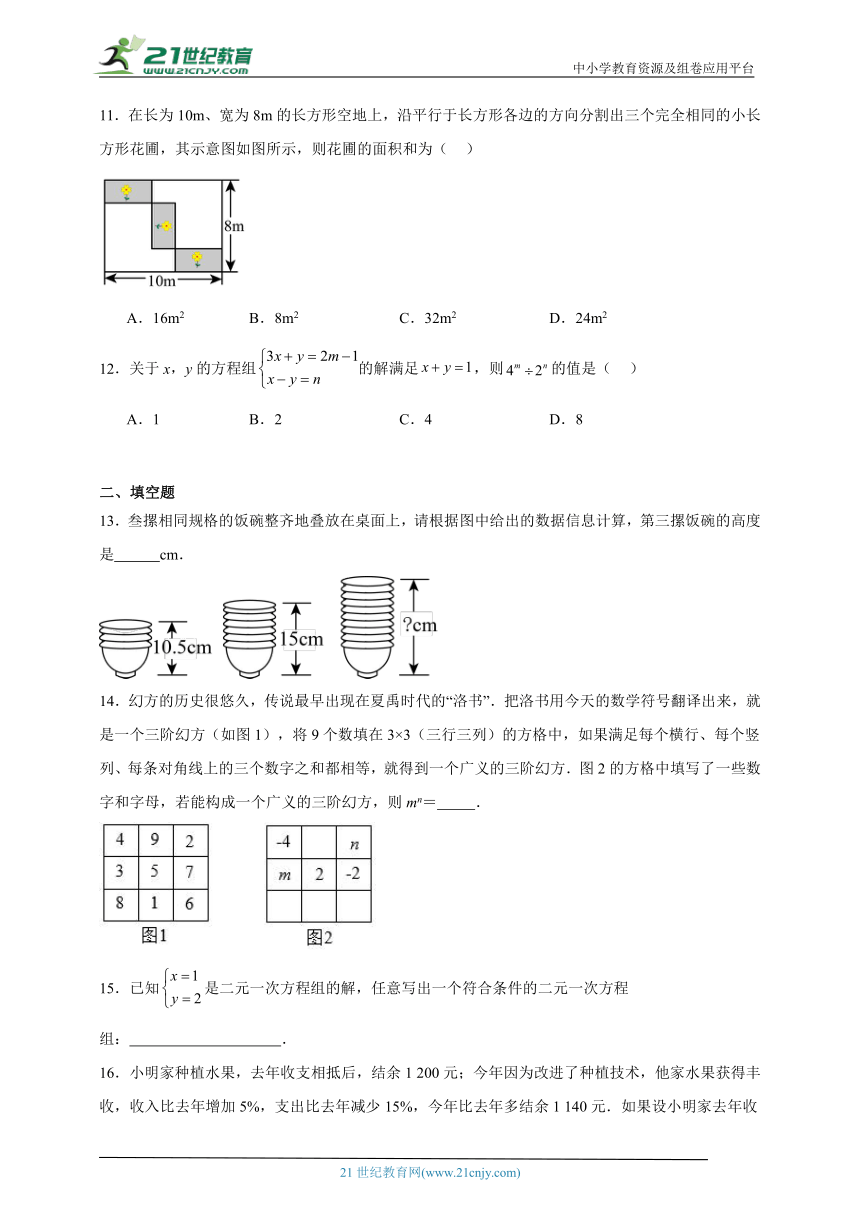
11.在长为10m、宽为8m的长方形空地上,沿平行于长方形各边的方向分割出三个完全相同的小长方形花圃,其示意图如图所示,则花圃的面积和为( )
A.16m2 B.8m2 C.32m2 D.24m2
12.关于x,y的方程组的解满足,则的值是( )
A.1 B.2 C.4 D.8
二、填空题
13.叁摞相同规格的饭碗整齐地叠放在桌面上,请根据图中给出的数据信息计算,第三摞饭碗的高度是 cm.
14.幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”.把洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图1),将9个数填在3×3(三行三列)的方格中,如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图2的方格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则mn= .
15.已知是二元一次方程组的解,任意写出一个符合条件的二元一次方程组: .
16.小明家种植水果,去年收支相抵后,结余1 200元;今年因为改进了种植技术,他家水果获得丰收,收入比去年增加5%,支出比去年减少15%,今年比去年多结余1 140元.如果设小明家去年收入x元,支出为y元,那么:
(1)将有关的数据填写在下表中:
项目 收入(元) 支出(元) 结余
去年 x y 1 200
今年 2 340
(2)根据表格列方程组 ,解得 .
17.已知等式对一切实数都成立,则= .
三、解答题
18.某商场从厂家购进了两种品牌篮球共80个,已知购买品牌篮球的总价比购买品牌篮球总价的2倍还多200元,品牌篮球每个进价100元,品牌篮球每个进价80元.
(1)求购进两种品牌篮球各多少个?
(2)在销售过程中,品牌篮球每个售价150元,售出30个后出现滞销;商场决定打折出售剩余的品牌篮球,品牌篮球每个按进价加价20%销售,很快全部售出,两种品牌篮球全部售出后共获利2080元,求品牌篮球打几折出售?
19.甲仓库和乙仓库共存粮450吨,现从甲仓库运出存量的,从乙仓库运出存粮的,结果乙仓库所余的粮食比甲仓库所余的粮食多30吨.求甲、乙仓库原来各存粮多少吨?
20.一个长方体的包装盒由1个侧面和2个底面组成.如果每张白卡纸可以做2个侧面,或者做3个底面,现有14张白卡纸,那么用多少张白卡纸做侧面,多少张白卡纸做底面,做出的侧面和底面恰好能配成包装盒?
21.某车间22名工人生产螺钉和螺母,每人每天平均生产螺钉12个或螺母20个,一个螺钉要配两个螺母,为使每天的产品刚好配套,应如何安排?
22.如图,块相同的长方形地砖拼成一个长方形,每块长方形地砖的长和宽分别是多少?
23.在一次知识竞赛中,学校为获得一等奖和二等奖共名学生购买奖品,共花费元,其中一等奖奖品每件元,二等奖奖品每件元,求获得一等奖和二等奖的学生分别有多少名.(请用方程组求解)
24.在数学著作《九章算术》中有这样一个问题:“今有牛五,羊二,值金十九两;牛二羊五,值金十六两,问牛羊各值金几何?”译文:“五头牛和两只羊共值金19两,两头牛和五只羊共值金16两,问牛和羊各值金多少两?”请你解决这个问题.
《7.3二元一次方程组的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D C D D C D C A
题号 11 12
答案 D D
1.D
【分析】本题主要考查由实际问题抽象出二元一次方程组.设这种出租车的起步价为x元,超过后每千米收费y元,根据题意列出二元一次方程组,即可求解.
【详解】解:设这种出租车的起步价为x元,超过后每千米收费y元,根据题意得,
,
故选:D.
2.B
【详解】∵关于x、y的二元一次方程组为
①②,得,
∴,∵,∴,∴.
3.D
【分析】首先设台大收割机和台小收割机每小时收割水稻分别是公顷、公顷,再根据“台大收割机和台小收割机同时工作h共收割水稻”,得到;再根据“台大收割机和台小收割机同时工作h共收割水稻”,得到.联立方程组,即可得到正确的选项.
【详解】台大收割机和台小收割机每小时收割水稻分别是公顷、公顷,
根据题意得:.
故选:D.
【点睛】本题考查二元一次方程组的实际应用问题,解本题的关键在理解题意,并列出二元一次方程组.
4.C
【分析】设上等草一捆为根,下等草一捆为根,根据“卖五捆上等草的根数减去11根,就等于七捆下等草的根数;卖七捆上等草的根数减去25根,就等于五捆下等草的根数.”列出方程组,即可求解.
【详解】解:设上等草一捆为根,下等草一捆为根,根据题意得:
.
故选:C
【点睛】本题主要考查了二元一次方程组的应用,明确题意,准确得到等量关系是解题的关键.
5.D
【分析】本题考查二元一次方程组的实际应用,设十位数字是,个位数字是,由题意列方程组求解即可得到答案,读懂题意,准确列出二元一次方程组是解决问题的关键.
【详解】解:设十位数字是,个位数字是,
则,
解得,
原来的两位数是,
故选:D.
6.D
【分析】本题考查了二元一次方程组的应用,设有x人,羊价为y元,根据若每人出5钱,还差45钱,可得出,再根据若每人出7钱,多余3钱,可得出,然后联立,即可列出方程组求解即可.
【详解】解:设有x人,羊价为y元,
由题意得:,
由得,
将代入得:,
解得:,
将代入,得:,
,
故选:D.
7.C
【分析】本题主要考查了解二元一次方程组,熟练掌握解二元一次方程组的解法是解题的关键.先解二元一次方程组,再将二元一次方程组的解代入,求解即可得到答案.
【详解】解:,
由得:,即,
将代入可得:,
解得:,
方程组的解为:,
方程组的解也是方程的解,
,
解得:,
故选:C.
8.D
【分析】本题考查了列二元一次方程组,根据题意找到等量关系是解题的关键.
【详解】解:设小刚平均每小时植树x棵,小敏平均每小时植树y棵,
由题意可得:,
故选:D.
9.C
【分析】①把a=1代入方程组进行计算,求出x、 y的值,然后再代入x+y=2中,即可得出答案;
②把x=y时代入方程组中,进行计算,即可得出答案;
③先解方程组,用a表示出x、y的值,然后将x、y代入2+y中进行计算,即可得出答案.
【详解】解:①∵,
∴原方程组为,
∴,
把代入中,
∴左边,右边,
∴左边≠右边,
∴当时,方程组的解不是方程的解,故①错误;
②把代入方程组中,可得:
,
∴,故②正确;
③∵,
∴,
∴,
∴不论取什么实数,的值始终不变,故③正确;
综上所述,结论正确的是:②③,
故选:C.
【点睛】此题考查了二元一次方程组的解,解二元一次方程,准确计算出方程组的解是解题的关键.
10.A
【分析】本题考查了由实际问题抽象出二元一次方程组.设该店有客房x间,房客y人;每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间客房得出方程组即可.
【详解】解:设该店有客房x间,房客y人;根据题意得:
,
故选:A.
11.D
【解析】略
12.D
【分析】法一:利用加减法解方程组,用表示出,再将求得的代数式代入,得到的关系,最后将变形,即可解答.
法二:中得到,再根据求出代入代数式进行求解即可.
【详解】解:法一:,
得,
解得,
将代入,解得,
,
,
得到,
,
法二:
得:,即:,
∵,
∴,
,
故选:D.
【点睛】本题考查了根据二元一次方程解的情况求参数,同底数幂除法,幂的乘方,熟练求出的关系是解题的关键.
13.
【分析】观察第一摞和第二摞饭碗,可以发现饭碗的高度与饭碗的个数成一次函数关系,所以设一次函数的表达式(),通过第一摞和第二摞饭碗的高度和个数确定一次函数的表达式,第三摞有10个饭碗,利用一次函数表达式求出相应的高度.
【详解】解:设一摞饭碗的高度(cm)与饭碗个数(个)之间的函数表达式为(),
由题意知,当时,;当时,,把它们代入上式,
得,
解得
故.
第三摞饭碗共有个,
当时,,
故答案为:.
【点睛】本题主要考查了一次函数表达式,通过给定一次函数上的两个点,确定一次函数的表达式,准确求出一次函数的表达式是解决本题的关键.
14.1
【分析】由第二行方格的数字,字母,可以得出第二行的数字之和为m,然后以此得出可知第三行左边的数字为4,第一行中间的数字为m-n+4,第三行中间数字为n-6,第三行右边数字为,再根据对角线上的三个数字之和相等且都等于m可得关于m,n方程组,解出即可.
【详解】如图,根据题意,可得
第二行的数字之和为:m+2+(-2)=m
可知第三行左边的数字为:m-(-4)-m=4
第一行中间的数字为:m-n-(-4)=m-n+4
第三行中间数字为m-2-(m-n+4)=n-6
第三行右边数字为:m-n-(-2)=m-n+2
再根据对角线上的三个数字之和相等且都等于m可得方程组为:
解得
∴
故答案为:1
【点睛】本题考查了有理数加法,列代数式,以及二元一次方程组,解题的关键是根据表格,利用每行,每列,每条对角线上的三个数之和相等列方程.
15.(答案不唯一)
【分析】本题考查二元一次方程组的解.根据方程组的解,够造方程组即可.
【详解】解:∵,
∴,
∴二元一次方程组的解即为;
故答案为:(答案不唯一).
16. (1) (1+5%)x, (1-15%)y (2),
【解析】略
17.-2
【分析】等式对于一切的实数x值均成立,则说明等式的两边代数式相同,即根据题意列出关于A、B的二元一次方程组,解方程组即可求解.
【详解】根据题意有:,
解得:,
即,
故答案为:-2.
【点睛】本题考查了一元一次方程组的应用.解决本题的关键在于构造关于A、B的二元一次方程组;体现了转化思想的应用.
18.(1)购进品牌篮球50个,购进品牌篮球30个
(2)7折
【分析】(1)设购进品牌篮球个,则购进品牌篮球个,根据两种品牌篮球共80个和购买品牌篮球的总价比购买品牌篮球总价的2倍还多200元可列出方程组求解即可;
(2)设品牌篮球打折出售,根据两种品牌篮球全部售出后共获利2080元列出方程解决问题.
【详解】(1)解:设购进品牌篮球个,则购进品牌篮球个,
,
解得,
故购进品牌篮球50个,购进品牌篮球30个;
(2)解:设品牌篮球打折出售,依题意有:
,
即:,
解得:,
故品牌篮球打7折出售.
【点睛】本题考查了二元一次方程组的应用,一元一次方程的应用,掌握题意,找出题目中的等量关系,列出方程并解答是关键.
19.甲仓库原来存粮240吨,乙仓库原来存粮210吨
【分析】设甲仓库原来存粮吨,乙仓库原来存粮吨,根据“甲仓库和乙仓库共存粮450吨,现从甲仓库运出存量的,从乙仓库运出存粮的,结果乙仓库所余的粮食比甲仓库所余的粮食多30吨”,即可得出关于,的二元一次方程组,解之即可得出结论.
【详解】解:设甲仓库原来存粮吨,乙仓库原来存粮吨,
根据题意得:,
解得:.
答:甲仓库原来存粮240吨,乙仓库原来存粮210吨.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
20.用6张白卡纸做侧面,8张白卡纸做底面,做出的侧面和底面恰好能配成包装盒
【分析】设x张白卡纸做侧面,y张白卡纸做底面,根据“包装盒由1个侧面和2个底面组成.如果每张白卡纸可以做侧面2个,或者做底面3个,现有14张白卡纸”列出方程组求解即可.
【详解】解:设用x张白卡纸做侧面,y张白卡纸做底面,
由题意得,解得.
答:用6张白卡纸做侧面,8张白卡纸做底面,做出的侧面和底面恰好能配成包装盒.
【点睛】本题考查了二元一次方程组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组.
21.安排10人生产螺钉,12人生产螺母
【分析】本题考查二元一次方程组的应用,根据题意得出,再求解即可得出答案.
【详解】解:设安排人生产螺钉,人生产螺母,
根据题意列方程组得,
解得;
答:安排10人生产螺钉,12人生产螺母.
22.长方形地砖的长为,宽为
【分析】设每块长方形地砖的长为,宽为,根据图形之间的边长关系,列出方程组进行求解即可.
【详解】解:设每块长方形地砖的长为,宽为.
依题意得,
解得,
答:长方形地砖的长为,宽为.
【点睛】本题考查二元一次方程组的实际应用.解题的关键是正确的识图,理清边长之间的和差关系,正确的列出方程组.
23.获得一等奖的学生有名,二等奖的学生有名.
【分析】本题考查了二元一次方程组与实际问题的运用,设获得一等奖的学生有名,二等奖的学生有名,由一等奖和二等奖共名,共花费元,即可列方程组求解,认真审题,找到等量关系,列出方程组是解题的关键.
【详解】解:设获得一等奖的学生有名,二等奖的学生有名,依题意得,
,
解得,
答:获得一等奖的学生有名,二等奖的学生有名.
24.牛和羊各值金3两、2两
【分析】设牛和羊各值金x、y两,根据题意列出二元一次方程组,解方程组即可求解.
【详解】设牛和羊各值金x、y两,
根据题意有:,
解得:,
答:牛和羊各值金3两、2两.
【点睛】本题考查了二元一次方程组的应用,明确题意,列出方程组,是解答本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
7.3二元一次方程组的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某市出租车起步价所包含的路程为,超过的部分按每千米另收费.明明乘坐这种出租车走了,付了16元;盼盼乘坐这种出租车走了,付了28元.设这种出租车的起步价为元,超过后每千米收费元,则下列方程正确的是( )
A. B.
C. D.
2.已知关于x,y的二元一次方程组的解满足,则m的值为( )
A.0 B.1 C.2 D.3
3.台大收割机和台小收割机同时工作h共收割水稻,台大收割机和台小收割机同时工作h共收割水稻,设台大收割机和台小收割机每小时收割水稻分别是公顷、公顷,则下列列式正确的是( )
A. B.
C. D.
4.张三经营了一家草场,草场里面种植上等草和下等草.他卖五捆上等草的根数减去11根,就等于七捆下等草的根数;卖七捆上等草的根数减去25根,就等于五捆下等草的根数.设上等草一捆为根,下等草一捆为根,则下列方程正确的是( )
A. B. C. D.
5.一个两位数,十位数字比个位数字的2倍大1.若这个两位数减去36恰好等于个位数字与十位数字对调后所得的两位数,则这个两位数是( )
A.86 B.68 C.94 D.73
6.《九章算术》中记载“今有共买羊,人出五,不足四十五:人出七,则余三, 问人数、羊价各几何 ”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还多3钱, 问合伙人数、羊价各是多少?此问题中羊价为( )
A.150钱 B.155 钱 C.160钱 D.165钱
7.若方程组的解也是方程的解,则k的值为( )
A.7 B. C.10 D.15
8.在3月12日是植树节这天,小刚和小敏积极踊跃地参加植树活动,小刚平均每小时比小敏多植1棵树,小刚植树3小时,小敏植树2小时,两人一共植树18棵树.设小刚平均每小时植树x棵,小敏平均每小时植树y棵,那么根据题意,下列所列方程组中,正确的是( )
A. B.
C. D.
9.已知关于x、y的方程组,则下列结论中正确的是( )
①当a=1时,方程组的解也是方程x+y=2的解;②当x=y时,a=;③不论a取什么实数,2x+y的值始终不变.
A.①② B.①②③ C.②③ D.②
10.在明朝程大位《算法统宗》中有首住店诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗的大意是:一些客人到李三公的店中住宿,如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.设该店有客房x间,房客y人,则可列方程组为( )
A. B.
C. D.
11.在长为10m、宽为8m的长方形空地上,沿平行于长方形各边的方向分割出三个完全相同的小长方形花圃,其示意图如图所示,则花圃的面积和为( )
A.16m2 B.8m2 C.32m2 D.24m2
12.关于x,y的方程组的解满足,则的值是( )
A.1 B.2 C.4 D.8
二、填空题
13.叁摞相同规格的饭碗整齐地叠放在桌面上,请根据图中给出的数据信息计算,第三摞饭碗的高度是 cm.
14.幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”.把洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图1),将9个数填在3×3(三行三列)的方格中,如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图2的方格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则mn= .
15.已知是二元一次方程组的解,任意写出一个符合条件的二元一次方程组: .
16.小明家种植水果,去年收支相抵后,结余1 200元;今年因为改进了种植技术,他家水果获得丰收,收入比去年增加5%,支出比去年减少15%,今年比去年多结余1 140元.如果设小明家去年收入x元,支出为y元,那么:
(1)将有关的数据填写在下表中:
项目 收入(元) 支出(元) 结余
去年 x y 1 200
今年 2 340
(2)根据表格列方程组 ,解得 .
17.已知等式对一切实数都成立,则= .
三、解答题
18.某商场从厂家购进了两种品牌篮球共80个,已知购买品牌篮球的总价比购买品牌篮球总价的2倍还多200元,品牌篮球每个进价100元,品牌篮球每个进价80元.
(1)求购进两种品牌篮球各多少个?
(2)在销售过程中,品牌篮球每个售价150元,售出30个后出现滞销;商场决定打折出售剩余的品牌篮球,品牌篮球每个按进价加价20%销售,很快全部售出,两种品牌篮球全部售出后共获利2080元,求品牌篮球打几折出售?
19.甲仓库和乙仓库共存粮450吨,现从甲仓库运出存量的,从乙仓库运出存粮的,结果乙仓库所余的粮食比甲仓库所余的粮食多30吨.求甲、乙仓库原来各存粮多少吨?
20.一个长方体的包装盒由1个侧面和2个底面组成.如果每张白卡纸可以做2个侧面,或者做3个底面,现有14张白卡纸,那么用多少张白卡纸做侧面,多少张白卡纸做底面,做出的侧面和底面恰好能配成包装盒?
21.某车间22名工人生产螺钉和螺母,每人每天平均生产螺钉12个或螺母20个,一个螺钉要配两个螺母,为使每天的产品刚好配套,应如何安排?
22.如图,块相同的长方形地砖拼成一个长方形,每块长方形地砖的长和宽分别是多少?
23.在一次知识竞赛中,学校为获得一等奖和二等奖共名学生购买奖品,共花费元,其中一等奖奖品每件元,二等奖奖品每件元,求获得一等奖和二等奖的学生分别有多少名.(请用方程组求解)
24.在数学著作《九章算术》中有这样一个问题:“今有牛五,羊二,值金十九两;牛二羊五,值金十六两,问牛羊各值金几何?”译文:“五头牛和两只羊共值金19两,两头牛和五只羊共值金16两,问牛和羊各值金多少两?”请你解决这个问题.
《7.3二元一次方程组的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D C D D C D C A
题号 11 12
答案 D D
1.D
【分析】本题主要考查由实际问题抽象出二元一次方程组.设这种出租车的起步价为x元,超过后每千米收费y元,根据题意列出二元一次方程组,即可求解.
【详解】解:设这种出租车的起步价为x元,超过后每千米收费y元,根据题意得,
,
故选:D.
2.B
【详解】∵关于x、y的二元一次方程组为
①②,得,
∴,∵,∴,∴.
3.D
【分析】首先设台大收割机和台小收割机每小时收割水稻分别是公顷、公顷,再根据“台大收割机和台小收割机同时工作h共收割水稻”,得到;再根据“台大收割机和台小收割机同时工作h共收割水稻”,得到.联立方程组,即可得到正确的选项.
【详解】台大收割机和台小收割机每小时收割水稻分别是公顷、公顷,
根据题意得:.
故选:D.
【点睛】本题考查二元一次方程组的实际应用问题,解本题的关键在理解题意,并列出二元一次方程组.
4.C
【分析】设上等草一捆为根,下等草一捆为根,根据“卖五捆上等草的根数减去11根,就等于七捆下等草的根数;卖七捆上等草的根数减去25根,就等于五捆下等草的根数.”列出方程组,即可求解.
【详解】解:设上等草一捆为根,下等草一捆为根,根据题意得:
.
故选:C
【点睛】本题主要考查了二元一次方程组的应用,明确题意,准确得到等量关系是解题的关键.
5.D
【分析】本题考查二元一次方程组的实际应用,设十位数字是,个位数字是,由题意列方程组求解即可得到答案,读懂题意,准确列出二元一次方程组是解决问题的关键.
【详解】解:设十位数字是,个位数字是,
则,
解得,
原来的两位数是,
故选:D.
6.D
【分析】本题考查了二元一次方程组的应用,设有x人,羊价为y元,根据若每人出5钱,还差45钱,可得出,再根据若每人出7钱,多余3钱,可得出,然后联立,即可列出方程组求解即可.
【详解】解:设有x人,羊价为y元,
由题意得:,
由得,
将代入得:,
解得:,
将代入,得:,
,
故选:D.
7.C
【分析】本题主要考查了解二元一次方程组,熟练掌握解二元一次方程组的解法是解题的关键.先解二元一次方程组,再将二元一次方程组的解代入,求解即可得到答案.
【详解】解:,
由得:,即,
将代入可得:,
解得:,
方程组的解为:,
方程组的解也是方程的解,
,
解得:,
故选:C.
8.D
【分析】本题考查了列二元一次方程组,根据题意找到等量关系是解题的关键.
【详解】解:设小刚平均每小时植树x棵,小敏平均每小时植树y棵,
由题意可得:,
故选:D.
9.C
【分析】①把a=1代入方程组进行计算,求出x、 y的值,然后再代入x+y=2中,即可得出答案;
②把x=y时代入方程组中,进行计算,即可得出答案;
③先解方程组,用a表示出x、y的值,然后将x、y代入2+y中进行计算,即可得出答案.
【详解】解:①∵,
∴原方程组为,
∴,
把代入中,
∴左边,右边,
∴左边≠右边,
∴当时,方程组的解不是方程的解,故①错误;
②把代入方程组中,可得:
,
∴,故②正确;
③∵,
∴,
∴,
∴不论取什么实数,的值始终不变,故③正确;
综上所述,结论正确的是:②③,
故选:C.
【点睛】此题考查了二元一次方程组的解,解二元一次方程,准确计算出方程组的解是解题的关键.
10.A
【分析】本题考查了由实际问题抽象出二元一次方程组.设该店有客房x间,房客y人;每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间客房得出方程组即可.
【详解】解:设该店有客房x间,房客y人;根据题意得:
,
故选:A.
11.D
【解析】略
12.D
【分析】法一:利用加减法解方程组,用表示出,再将求得的代数式代入,得到的关系,最后将变形,即可解答.
法二:中得到,再根据求出代入代数式进行求解即可.
【详解】解:法一:,
得,
解得,
将代入,解得,
,
,
得到,
,
法二:
得:,即:,
∵,
∴,
,
故选:D.
【点睛】本题考查了根据二元一次方程解的情况求参数,同底数幂除法,幂的乘方,熟练求出的关系是解题的关键.
13.
【分析】观察第一摞和第二摞饭碗,可以发现饭碗的高度与饭碗的个数成一次函数关系,所以设一次函数的表达式(),通过第一摞和第二摞饭碗的高度和个数确定一次函数的表达式,第三摞有10个饭碗,利用一次函数表达式求出相应的高度.
【详解】解:设一摞饭碗的高度(cm)与饭碗个数(个)之间的函数表达式为(),
由题意知,当时,;当时,,把它们代入上式,
得,
解得
故.
第三摞饭碗共有个,
当时,,
故答案为:.
【点睛】本题主要考查了一次函数表达式,通过给定一次函数上的两个点,确定一次函数的表达式,准确求出一次函数的表达式是解决本题的关键.
14.1
【分析】由第二行方格的数字,字母,可以得出第二行的数字之和为m,然后以此得出可知第三行左边的数字为4,第一行中间的数字为m-n+4,第三行中间数字为n-6,第三行右边数字为,再根据对角线上的三个数字之和相等且都等于m可得关于m,n方程组,解出即可.
【详解】如图,根据题意,可得
第二行的数字之和为:m+2+(-2)=m
可知第三行左边的数字为:m-(-4)-m=4
第一行中间的数字为:m-n-(-4)=m-n+4
第三行中间数字为m-2-(m-n+4)=n-6
第三行右边数字为:m-n-(-2)=m-n+2
再根据对角线上的三个数字之和相等且都等于m可得方程组为:
解得
∴
故答案为:1
【点睛】本题考查了有理数加法,列代数式,以及二元一次方程组,解题的关键是根据表格,利用每行,每列,每条对角线上的三个数之和相等列方程.
15.(答案不唯一)
【分析】本题考查二元一次方程组的解.根据方程组的解,够造方程组即可.
【详解】解:∵,
∴,
∴二元一次方程组的解即为;
故答案为:(答案不唯一).
16. (1) (1+5%)x, (1-15%)y (2),
【解析】略
17.-2
【分析】等式对于一切的实数x值均成立,则说明等式的两边代数式相同,即根据题意列出关于A、B的二元一次方程组,解方程组即可求解.
【详解】根据题意有:,
解得:,
即,
故答案为:-2.
【点睛】本题考查了一元一次方程组的应用.解决本题的关键在于构造关于A、B的二元一次方程组;体现了转化思想的应用.
18.(1)购进品牌篮球50个,购进品牌篮球30个
(2)7折
【分析】(1)设购进品牌篮球个,则购进品牌篮球个,根据两种品牌篮球共80个和购买品牌篮球的总价比购买品牌篮球总价的2倍还多200元可列出方程组求解即可;
(2)设品牌篮球打折出售,根据两种品牌篮球全部售出后共获利2080元列出方程解决问题.
【详解】(1)解:设购进品牌篮球个,则购进品牌篮球个,
,
解得,
故购进品牌篮球50个,购进品牌篮球30个;
(2)解:设品牌篮球打折出售,依题意有:
,
即:,
解得:,
故品牌篮球打7折出售.
【点睛】本题考查了二元一次方程组的应用,一元一次方程的应用,掌握题意,找出题目中的等量关系,列出方程并解答是关键.
19.甲仓库原来存粮240吨,乙仓库原来存粮210吨
【分析】设甲仓库原来存粮吨,乙仓库原来存粮吨,根据“甲仓库和乙仓库共存粮450吨,现从甲仓库运出存量的,从乙仓库运出存粮的,结果乙仓库所余的粮食比甲仓库所余的粮食多30吨”,即可得出关于,的二元一次方程组,解之即可得出结论.
【详解】解:设甲仓库原来存粮吨,乙仓库原来存粮吨,
根据题意得:,
解得:.
答:甲仓库原来存粮240吨,乙仓库原来存粮210吨.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
20.用6张白卡纸做侧面,8张白卡纸做底面,做出的侧面和底面恰好能配成包装盒
【分析】设x张白卡纸做侧面,y张白卡纸做底面,根据“包装盒由1个侧面和2个底面组成.如果每张白卡纸可以做侧面2个,或者做底面3个,现有14张白卡纸”列出方程组求解即可.
【详解】解:设用x张白卡纸做侧面,y张白卡纸做底面,
由题意得,解得.
答:用6张白卡纸做侧面,8张白卡纸做底面,做出的侧面和底面恰好能配成包装盒.
【点睛】本题考查了二元一次方程组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组.
21.安排10人生产螺钉,12人生产螺母
【分析】本题考查二元一次方程组的应用,根据题意得出,再求解即可得出答案.
【详解】解:设安排人生产螺钉,人生产螺母,
根据题意列方程组得,
解得;
答:安排10人生产螺钉,12人生产螺母.
22.长方形地砖的长为,宽为
【分析】设每块长方形地砖的长为,宽为,根据图形之间的边长关系,列出方程组进行求解即可.
【详解】解:设每块长方形地砖的长为,宽为.
依题意得,
解得,
答:长方形地砖的长为,宽为.
【点睛】本题考查二元一次方程组的实际应用.解题的关键是正确的识图,理清边长之间的和差关系,正确的列出方程组.
23.获得一等奖的学生有名,二等奖的学生有名.
【分析】本题考查了二元一次方程组与实际问题的运用,设获得一等奖的学生有名,二等奖的学生有名,由一等奖和二等奖共名,共花费元,即可列方程组求解,认真审题,找到等量关系,列出方程组是解题的关键.
【详解】解:设获得一等奖的学生有名,二等奖的学生有名,依题意得,
,
解得,
答:获得一等奖的学生有名,二等奖的学生有名.
24.牛和羊各值金3两、2两
【分析】设牛和羊各值金x、y两,根据题意列出二元一次方程组,解方程组即可求解.
【详解】设牛和羊各值金x、y两,
根据题意有:,
解得:,
答:牛和羊各值金3两、2两.
【点睛】本题考查了二元一次方程组的应用,明确题意,列出方程组,是解答本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
