9.3 用表格表示变量之间的关系 同步练习(含解析)
文档属性
| 名称 | 9.3 用表格表示变量之间的关系 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 800.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-03 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
9.3用表格表示变量之间的关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.弹挂上物体后伸长,已知一弹的长度()与所挂物体的质()之间的关系如表:下列说法错误的是( )
物体的质量() 0 1 2 3 4 5
弹簧的长度() 10 12.5 15 17.5 20 22.5
A.在没挂物体时,弹簧的长度为.
B.弹簧的长度随物体的质量的变化而变化,弹簧的长度是自变量,物体的质量是弹簧的长度的函数
C.在弹簧能承受的范围内,所挂物体的质量每增加,弹簧的长度就增加
D.在弹簧能承受的范围内,当物体的质量为时,弹簧的长度为
2.小文去水果店买西瓜,如图是称西瓜所用的电子秤显示屏上的数据,则其中的变量是( )
A.金额 B.数量 C.单价 D.金额和数量
3.弹簧挂上物体后会伸长,测得一弹簧的长度与所挂物体质量之间有如下关系(其中)
0 1 2 3 4 5
10 10.5 11 11.5 12 12.5
下列说法不正确的是( )
A.与都是变量,且是自变量,是因变量
B.弹簧不挂重物时的长度为
C.所挂物体质量每增加,弹簧长度增加
D.所挂物体质量为时,弹簧长度为
4.一个学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如表数据:
支撑物的高度 10 20 30 40 50
小车下滑的时间 4.23 3.00 2.45 2.13 1.89
支撑物的高度 60 70 80 90 100
小车下滑的时间 1.71 1.59 1.50 1.41 1.35
下列说法正确的是( )
A.当时, B.h每增加,减小
C.随着h逐渐升高,t也逐渐变大 D.随着h逐渐升高,小车下滑的平均速度逐渐加快
5.(古代文化)漏刻是我国古代的一种计时工具.小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现了水位h(单位:)和时间t(单位:)两个变量之间的关系.下表是小明记录的部分数据,当h为时,对应的时间t为( )
… 1 2 3 4 …
… …
A. B. C. D.
6.某文具店老板购进一批荧光笔,销量(支)与销售额(元)的关系如下表所示:
销量支 …
销售额元 …
则销售额与销量的函数关系式为( )
A. B. C. D.
7.某地区用电量与应缴电费之间的关系如下表:则下列叙述错误的是( )
用电量(千瓦 时) 1 2 3 4 …
应缴电费(元) …
A.用电量是自变量,应缴电费是因变量
B.用电量每增加1千瓦 时,电费增加元
C.若用电量为5千瓦 时,则应缴电费元
D.若小明的应缴电费比小红多2元,则小明的用电量比小红的用电量多千瓦 时
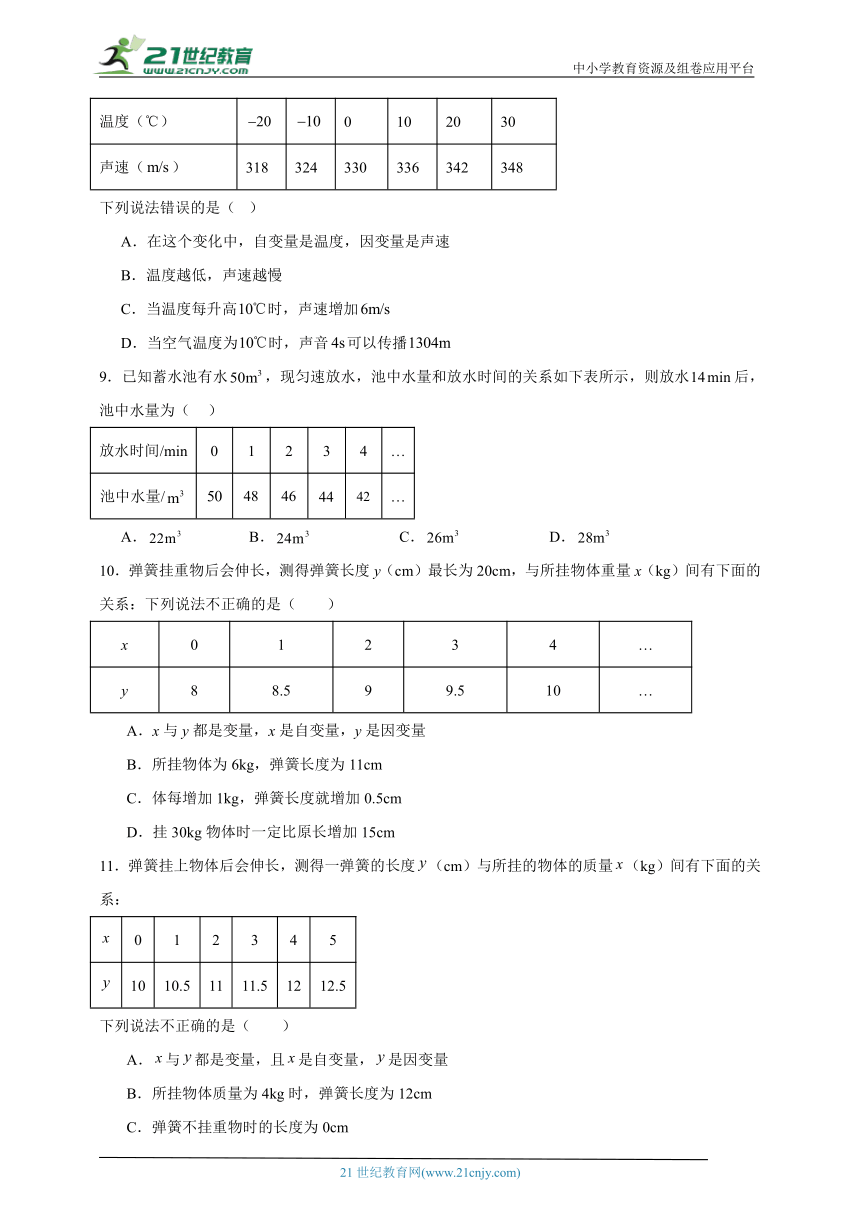
8.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据如下:
温度(℃) 0 10 20 30
声速() 318 324 330 336 342 348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越低,声速越慢
C.当温度每升高时,声速增加
D.当空气温度为时,声音可以传播
9.已知蓄水池有水,现匀速放水,池中水量和放水时间的关系如下表所示,则放水后,池中水量为( )
放水时间/min 0 1 2 3 4 …
池中水量/ …
A. B. C. D.
10.弹簧挂重物后会伸长,测得弹簧长度y(cm)最长为20cm,与所挂物体重量x(kg)间有下面的关系:下列说法不正确的是( )
x 0 1 2 3 4 …
y 8 8.5 9 9.5 10 …
A.x与y都是变量,x是自变量,y是因变量
B.所挂物体为6kg,弹簧长度为11cm
C.体每增加1kg,弹簧长度就增加0.5cm
D.挂30kg物体时一定比原长增加15cm
11.弹簧挂上物体后会伸长,测得一弹簧的长度(cm)与所挂的物体的质量(kg)间有下面的关系:
0 1 2 3 4 5
10 10.5 11 11.5 12 12.5
下列说法不正确的是( )
A.与都是变量,且是自变量,是因变量
B.所挂物体质量为4kg时,弹簧长度为12cm
C.弹簧不挂重物时的长度为0cm
D.与之间的关系式为
12.小邢到单位附近的加油站加油.如图所示的是小邢所用的加油机上的数据显示牌,则数据中的变量是( )
A.金额 B.数量 C.单价 D.金额和数量
二、填空题
13.一个蓄水池有水,打开放水闸门匀速放水,水池中的水量和放水时间的关系如表:
放水时间(min) 1 2 3 4 …
水池中水量() 48 46 44 42 …
则放水14min时,水池中有水 .
14.某商店在开学季,书包薄利多销的促销活动.原价为元,随着不同幅度的降价,日销量(单位:件)发生相应的变化:从表中可以看出,每降价元,日销量增加 件.
降价(元)
日销量(件)
15.声音在空气中传播的速度y(单位:)与气温x(单位:)的关系如下表:
气温 0 5 10 15 20
声速 331 334 337 340 343
照此规律可以发现,当气温为 时,声速达到.
16.科学家认为二氧化碳的释放量越来越多是全球变暖的原因之一.下表1950-2020年全球排放的二氧化碳量:
年份 1950 1960 1970 1980 1990 2000 2010 2020
全球排放量/百万吨 6002 9475 14989 19287 22588 24688 34180 35962
其中因变量为 .
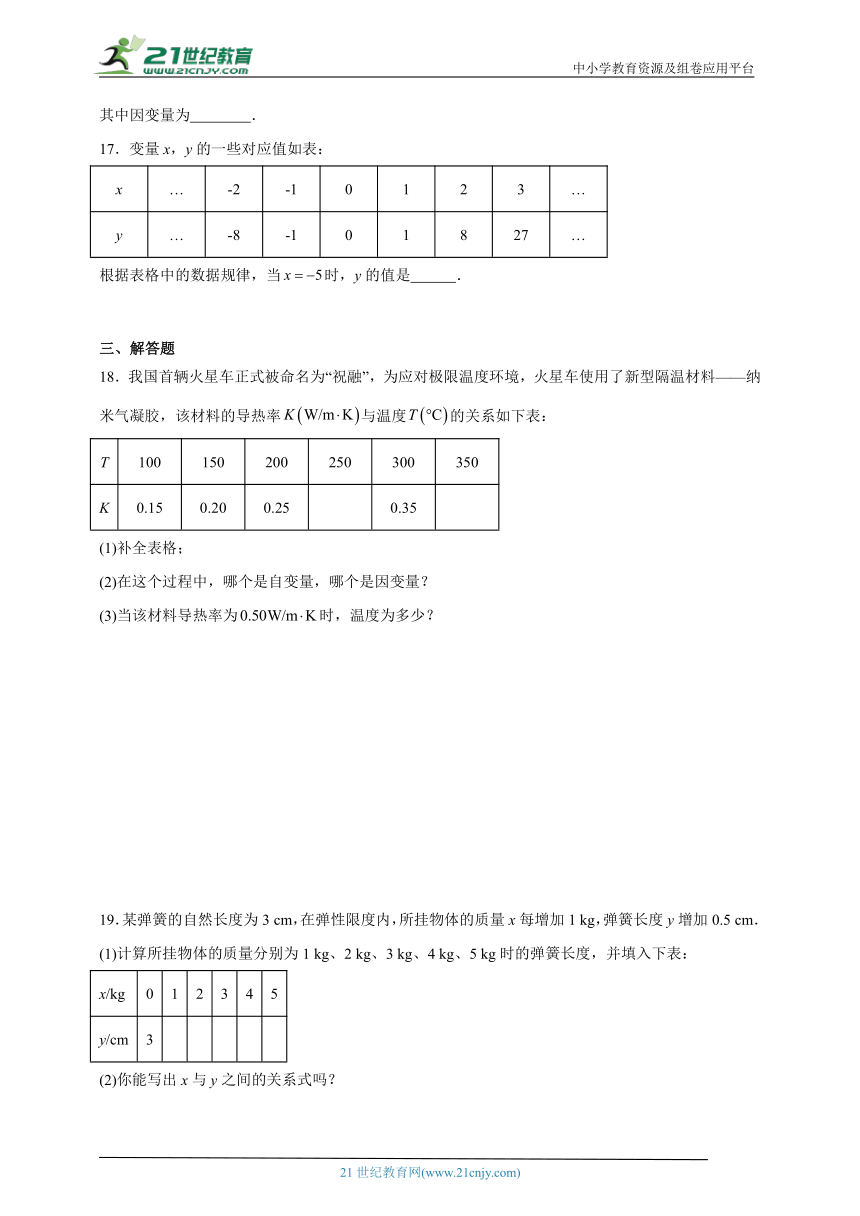
17.变量x,y的一些对应值如表:
x … -2 -1 0 1 2 3 …
y … -8 -1 0 1 8 27 …
根据表格中的数据规律,当时,y的值是 .
三、解答题
18.我国首辆火星车正式被命名为“祝融”,为应对极限温度环境,火星车使用了新型隔温材料——纳米气凝胶,该材料的导热率与温度的关系如下表:
T 100 150 200 250 300 350
K 0.15 0.20 0.25 0.35
(1)补全表格;
(2)在这个过程中,哪个是自变量,哪个是因变量?
(3)当该材料导热率为时,温度为多少?
19.某弹簧的自然长度为3 cm,在弹性限度内,所挂物体的质量x每增加1 kg,弹簧长度y增加0.5 cm.
(1)计算所挂物体的质量分别为1 kg、2 kg、3 kg、4 kg、5 kg时的弹簧长度,并填入下表:
x/kg 0 1 2 3 4 5
y/cm 3
(2)你能写出x与y之间的关系式吗?
20.从高处抛下一个物体,测定高度与落地时间的关系如下表:
高度 5 10 15 20 25
落地时间 1 2
估计从处抛下,需多少时间落地?
21.某电影院地面的一部分观影席座位分布是扇形,其每排座位数按下列规律设置:
排数 1 2 3 4 5 6 …
座位数 60 64 68 72 76 ______ …
(1)请将表格补充完整;
(2)根据表格中的数据,请说明座位数是随排数的增长而怎样变化的?
(3)当排数是7时,该排的座位数是多少?
22.小华粉刷他的卧室共花去10小时,他记录的完成工作量的百分数如下:
时间(小时) 1 2 3 4 5 6 7 8 9 10
完成的百分数 5 25 35 50 50 65 70 80 95 100
(1)5小时他完成工作量的百分数是______;
(2)小华在______时间里工作量最大;
(3)如果小华在早晨8时开始工作,则他在______时间没有工作.
23.心理学研究发现,学生对概念的接受能力y与提出概念所用的时间x(分钟)之间有如下关系:
x 2 5 7 10 12 13 14 17 20 …
y 47.8 53.5 56.3 59 59.8 59.9 59.8 58.3 55 …
根据以上信息,回答下列问题:
(1)上表反映的两个变量中,自变量是__________,因变量是__________.
(2)当提出概念所用的时间为7分钟时,学生的接受能力是多少?
(3)在上表中,当提出概念所用的时间为多少分钟时,学生的接受能力最强?
(4)根据表中数据,说说当提出概念所用的时间在2~20分钟时,学生对概念的接受能力是怎样变化的?
24.在烧开水时,水温达到就会沸腾(标准大气压下),下表是某同学做“观察水的沸腾”实验时记录的数据:
时间 0 2 4 6 8 10 12 14 …
水的温度 30 44 58 72 86 100 100 100 …
(1)如表反映了哪两个量之间的关系?哪个是自变量?哪个是因变量?
(2)水的温度是如何随着时间的变化而变化的?
(3)时间每增加,水的温度如何变化?
(4)为了节约能源,你认为应在什么时间停止烧水?
《9.3用表格表示变量之间的关系》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B D D D D A D D A D
题号 11 12
答案 C D
1.B
【分析】根据表格数据,自变量x所挂物体的重量与因变量y弹簧的长度的关系,依次判断正误即可.
【详解】解:根据条件,可列关系式为:.
A、在没挂物体时,弹簧的长度为,根据图表,当质量时,,故此选项正确,不符合题意;
B、反映了所挂物体的质量和弹簧的长度之间的关系,所挂物体的质量是自变量;弹簧的长度是因变量,故此选项错误,符合题意;
C、在弹簧能承受的范围内,所挂物体的质量每增加,弹簧的长度就增加,故此选项正确,不符合题意;
D、由关系式,,解得,在弹簧的弹性范围内,故此选项正确,不符合题意;
故选:B.
【点睛】此题考查了函数关系式,主要考查了函数的定义和结合几何图形列函数关系式.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
2.D
【分析】本题考查变量与常量,解答本题的关键要明确:变化的量叫变量,恒定不变的量叫常量.
根据变化的量叫变量,恒定不变的量叫常量逐个判断即可得到答案.
【详解】解:由题意可得,金额单价数量,单价不变,数量与金额是变化的量,
∴单价常量,数量与金额是变量,
故选:D.
3.D
【分析】根据变量与常量,用表格表示变量之间的关系,结合表格中数据的变化规律逐项进行判断即可.
【详解】解:A.x与y都是变量,且x是自变量,y是因变量,是正确的,因此该选项不符合题意;
B.弹簧不挂重物时的长度,即当时y的值,此时,是正确的,因此该选项不符合题意;
C.物体质量x每增加,弹簧长度增加,是正确的,因此该选项不符合题意;
D.根据物体质量x每增加,弹簧长度增加,可得出所挂物体质量为时,弹簧长度为,原选项错误,因此该选项符合题意;
故选:D.
【点睛】本题考查常量与变量,用表格表示变量之间的关系,理解和发现表格中数据的变化规律是解决问题的关键.
4.D
【分析】本题考查了用表格表示变量间的关系,观察表格获得有效信息是解题的关键.
通过分析表格数据,理解变量之间的关系以及随着自变量的变化因变量的变化趋势,即可得出答案.
【详解】解:A.当时,,故选项错误;
B.h每增加,减小的值不一定,故选项错误;
C.随着h逐渐升高,t逐渐变小,故选项错误;
D. 随着h逐渐升高,小车下滑的时间逐渐变小,小车下滑的平均速度逐渐加快,故选项正确;
故选:.
5.D
【分析】本题考查函数的表示方法,找到变量之间的变化规律是解题的关键.由表格可知,增加,增加,据此列方程并求解即可.
【详解】解:由表格可知,增加,增加,则,
解得,
当为时,对应的时间为.
故选:D
6.A
【分析】此题考查的是函数的表示方法,观察表格中的数据发现:销售额是销售数量的倍,据此列出函数关系式;
【详解】解:表格中的数据发现:销售额是销售数量的倍,
∴销售额与销量的函数关系式为
故选:A.
7.D
【分析】根据用电量与应缴电费之间成正比例关系逐项判断即可.
【详解】解:A、用电量是自变量,应缴电费是因变量,故本选项叙述正确,不符合题意;
B、若用电量每增加千瓦 时,则电费增加元,故本选项叙述正确,不符合题意;
C、若用电量为5千瓦 时,则应缴电费元,故本选项叙述正确,不符合题意;
D、若小明的应缴电费比小红多元,则小明的用电量比小红的用电量多千瓦·时,故本选项叙述错误,符合题意.
故选:D.
【点睛】本题考查了用表格表示变量之间的关系,列表法能具体的反映自变量与因变量的数值对应关系.
8.D
【分析】本题考查用表格表示变量之间的关系,从表格中获取信息,逐一进行分析即可.
【详解】解:A.∵在这个变化中,自变量是温度,因变量是声速,∴说法正确,不符合题意;
B.∵根据表中数据,可得温度越低,声速越慢,∴说法正确,不符合题意;
C.∵,,,,,
∴当温度每升高,声速增加,∴说法正确,不符合题意;
D.∵,
∴当空气温度为时,声音可以传播,∴说法错误,符合题意.
故选:D.
9.A
【分析】依据题意,通过水池中的水量和放水时间的关系表,分析出水池中水量每分钟减少,从而可得函数关系式,最后可求出当放水时水池中的水量.
【详解】解:由题意知,水池中水量每分钟减少,
设水池中剩余水量为,放水时间为
∴,
∴当时,.
即当放水时,水池中有水.
故选:A.
【点睛】本题主要考查了函数的表示方法,需要通过读懂题意,识别函数关系式是解题的关键.
10.D
【分析】弹簧长度随所挂物体的重量的变化而变化,由表格数据可知物体每增加,弹簧长度就增加,可以计算当所挂物体为或时弹簧的长度,但应注意弹簧的最大长度为.
【详解】解:A.因为弹簧长度随所挂物体的重量的变化而变化,所以是自变量,是因变量.故本选项正确,不符合题意;
B.当所挂物体为时,弹簧的长度为.故本选项正确,不符合题意;
C.从表格数据中分析可知,物体每增加,弹簧长度就增加.故本选项正确,不符合题意;
D.当所挂物体为时,弹簧长度为.故本选项不正确,符合题意.
故选:D
【点睛】本题考查了变量、自变量、因变量的概念,认真审题能从题目中抽取出有效信息是解题的关键.
11.C
【分析】根据挂重物与弹簧伸长的长度,可得答案.
【详解】解:A、x和y都是变量,且x是自变量,y是因变量,故A正确;
B、当时,,故B正确;
C、当时,,故C错误;
D、由挂重物与弹簧伸长的长度,得,故D正确;
故选:C.
【点睛】本题考查了函数关系式,利用挂重物与弹簧伸长的长度得出函数关系式是解题关键.
12.D
【分析】本题考查了常量与变量,掌握相关定义是解题关键.在一个变化的过程中,数值发生变化的量称为变量,数值始终不变的量称为常量,据此即可作答.
【详解】解:数据中的变量是金额和数量,
故选:D.
13.22
【分析】根据表格中“放水时间”与“水池中水量”之间的变化规律可得答案.
【详解】解:由表格中“放水时间”与“水池中水量”对应值的变化规律可知,
放水时间每增加1min,水池中水量就减少2,
所以当放水时间为14min时,水池中水量为48﹣2×(14﹣1)=22(),
故答案为:22.
【点睛】本题考查用表格表示变量间的关系,掌握表格中两个变量的变化规律是解决问题的关键.
14.30
【分析】本题考查了变量与常量,根据表格得到变量间的关系即可.
【详解】解:由表格可知,每降价元,日销量增加(件),
故答案为:30.
15.
【分析】本题考查了利用表格表示变量之间的关系.观察图表数据,气温每升高,声速增加,然后结合当气温为,音速增加,从而可得答案.
【详解】解:∵气温每升高,音速增加,
当气温为,音速增加,
∴当声音在空气中的传播速度为,气温是,
故答案为:.
16.二氧化碳的释放量
【分析】根据自变量、因变量的定义分别得出即可;
【详解】解:由表可知,二氧化碳的释放量随着年份的增加而增大.
∴因变量为二氧化碳的释放量;
故答案为:二氧化碳的释放量;
【点睛】此题主要考查了自变量、因变量的定义,解题的关键是熟记定义进行判断.
17.-125
【分析】根据表格中两个变量对应值的变化规律得出答案.
【详解】解:由表格中两个变量对应值的变化规律可知,y=x3,
当x=﹣5时,y=(﹣5)3=﹣125,
故答案为:﹣125.
【点睛】本题考查了用表格表示变量间的关系,发现表格中两个变量对应值的变化规律是解题的关键.
18.(1)见解析
(2)温度是自变量,导热率是因变量
(3)
【分析】本题考查了函数的表示法,观察表格得出温度每增加,导热率增加是解答本题的关键.
(1)根据导热率变化规律计算即可;
(2)根据导热率随着温度的变化而变化即可解答;
(3)根据度每增加,导热率增加求解即可.
【详解】(1)观察表格可知温度每增加,导热率增加,
,
,
T 100 150 200 250 300 350
K 0.15 0.20 0.25 0.30 0.35 0.40
(2)∵导热率随着温度的变化而变化,
∴温度是自变量,导热率是因变量;
(3).
19.(1)3.5;4;4.5;5;5.5
(2)y=3+0.5x
【详解】试题分析:(1)据填表即可;
(2)利用表格中数据分析得出即可;
试题解析:(1)
(2)y=0.5x+3.
20.估计从处抛下,需落地
【分析】本题主要考查了函数关系是以及函数的表示方法等知识,学会观察表格是解决本题的关键.根据下落高度与时间进行估算即可.
【详解】解:由表格可知,从到,落地时间的增加量为,
所以从到,落地时间的增加量应小于,
即时的落地时间应在到之间.
故估计从处抛下,需落地.
21.(1)80
(2)座位数随排数的增长而增长
(3)84
【分析】本题考查用表格表示变量间的关系,找到数据的变化规律是解题的关键.
(1)由表格可知,当排数每增加1排时,座位数就会增加4,据此作答即可;
(2)根据表格中的数据,可得出座位数是随排数的增长的变化情况;
(3)根据表格中的规律,计算出当排数是7时,该排的座位数.
【详解】(1)由表格可知,当排数每增加1排时,座位数就会增加4,
当排数为6排时,座位数为80.
故答案为:80;
(2)根据表格中的数据,可得出座位数随排数的增长而增长.
(3),
答:当排数是7时,该排的座位数是84.
22.(1)
(2)第二小时
(3)时
【分析】本题考查了函数的表示方法,比较简单,阅读图表数据,准确获取信息是解题的关键.
(1)根据图表数据解答即可;
(2)根据数据找出完成百分数最多的时间即可;
(3)根据完成的百分数,开始工作后4到5小时没有工作,然后求出相应的时间即可.
【详解】(1)5小时他完成工作量的百分数是;
故答案为:;
(2)由图表可知,在第二小时完成的百分数最大是,所以,在第二小时时间里工作量最大;
故答案为:第二小时;
(3)开始工作小时工作量都是没有发生变化,
早晨8时开始工作,
在时时间没有工作.
故答案为:时.
23.(1)提出概念所用的时间x;学生对概念的接受能力y
(2)56.3
(3)13分钟
(4)见解析
【分析】此题主要考查了用表格表示变量间的关系,正确利用表格中数据得出结论是解题关键.
(1)利用表格中数据得出答案;
(2)利用表格中数据得出答案;
(3)利用表格中数据得出答案;
(4)先根据表格可知:当时,y的值最大是59.9,当时,y随x的增大而增大,当时,y随x的增大而减小,从而得出答案.
【详解】(1)解:上表反映的两个变量中,自变量是提出概念所用的时间x,因变量是学生对概念的接受能力y.
故答案为:提出概念所用的时间x;学生对概念的接受能力y
(2)解:观察表格可知,当时,,
∴当提出概念所用的时间为7分钟时,学生的接受能力是56.3.
(3)解:∵当时,y的值最大是59.9,
∴当提出概念所用的时间为13分钟时,学生的接受能力最强.
(4)解:当时,学生的接受能力y随提出概念所用的时间x的增加而增大;
当时,学生的接受能力y随提出概念所用的时间x的增加而减小.
24.(1)反映了水的温度与时间的关系,时间是自变量,水的温度是因变量
(2)水的温度随着时间的增加而增加,到时恒定
(3)时间每增加,水的温度增加,到时恒定
(4)为了节约能源,应在后停止烧水
【分析】本题主要考查了常量与变量,根据表格中数据分别分析得出是解题关键.
(1)在函数中,给一个变量x一个值,另一个变量y就有对应的值,则x是自变量,y是因变量,据此即可判断;
(2)根据表格中数据得出水的温度变化即可;
(3)根据表格中数据得出水的温度变化即可;
(4)根据表格中数据得出答案即可.
【详解】(1)解:反映了水的温度与时间的关系,时间是自变量,水的温度是因变量,
答:反映了水的温度与时间的关系,时间是自变量,水的温度是因变量;
(2)解:水的温度随着时间的增加而增加,到时恒定,
答:水的温度随着时间的增加而增加,到时恒定;
(3)解:时间每增加,水的温度增加,到时恒定,
答:时间每增加,水的温度增加,到时恒定
(4)解:为了节约能源,应在10分钟后停止烧水,
答:为了节约能源,应在10分钟后停止烧水.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
9.3用表格表示变量之间的关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.弹挂上物体后伸长,已知一弹的长度()与所挂物体的质()之间的关系如表:下列说法错误的是( )
物体的质量() 0 1 2 3 4 5
弹簧的长度() 10 12.5 15 17.5 20 22.5
A.在没挂物体时,弹簧的长度为.
B.弹簧的长度随物体的质量的变化而变化,弹簧的长度是自变量,物体的质量是弹簧的长度的函数
C.在弹簧能承受的范围内,所挂物体的质量每增加,弹簧的长度就增加
D.在弹簧能承受的范围内,当物体的质量为时,弹簧的长度为
2.小文去水果店买西瓜,如图是称西瓜所用的电子秤显示屏上的数据,则其中的变量是( )
A.金额 B.数量 C.单价 D.金额和数量
3.弹簧挂上物体后会伸长,测得一弹簧的长度与所挂物体质量之间有如下关系(其中)
0 1 2 3 4 5
10 10.5 11 11.5 12 12.5
下列说法不正确的是( )
A.与都是变量,且是自变量,是因变量
B.弹簧不挂重物时的长度为
C.所挂物体质量每增加,弹簧长度增加
D.所挂物体质量为时,弹簧长度为
4.一个学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如表数据:
支撑物的高度 10 20 30 40 50
小车下滑的时间 4.23 3.00 2.45 2.13 1.89
支撑物的高度 60 70 80 90 100
小车下滑的时间 1.71 1.59 1.50 1.41 1.35
下列说法正确的是( )
A.当时, B.h每增加,减小
C.随着h逐渐升高,t也逐渐变大 D.随着h逐渐升高,小车下滑的平均速度逐渐加快
5.(古代文化)漏刻是我国古代的一种计时工具.小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现了水位h(单位:)和时间t(单位:)两个变量之间的关系.下表是小明记录的部分数据,当h为时,对应的时间t为( )
… 1 2 3 4 …
… …
A. B. C. D.
6.某文具店老板购进一批荧光笔,销量(支)与销售额(元)的关系如下表所示:
销量支 …
销售额元 …
则销售额与销量的函数关系式为( )
A. B. C. D.
7.某地区用电量与应缴电费之间的关系如下表:则下列叙述错误的是( )
用电量(千瓦 时) 1 2 3 4 …
应缴电费(元) …
A.用电量是自变量,应缴电费是因变量
B.用电量每增加1千瓦 时,电费增加元
C.若用电量为5千瓦 时,则应缴电费元
D.若小明的应缴电费比小红多2元,则小明的用电量比小红的用电量多千瓦 时
8.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据如下:
温度(℃) 0 10 20 30
声速() 318 324 330 336 342 348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越低,声速越慢
C.当温度每升高时,声速增加
D.当空气温度为时,声音可以传播
9.已知蓄水池有水,现匀速放水,池中水量和放水时间的关系如下表所示,则放水后,池中水量为( )
放水时间/min 0 1 2 3 4 …
池中水量/ …
A. B. C. D.
10.弹簧挂重物后会伸长,测得弹簧长度y(cm)最长为20cm,与所挂物体重量x(kg)间有下面的关系:下列说法不正确的是( )
x 0 1 2 3 4 …
y 8 8.5 9 9.5 10 …
A.x与y都是变量,x是自变量,y是因变量
B.所挂物体为6kg,弹簧长度为11cm
C.体每增加1kg,弹簧长度就增加0.5cm
D.挂30kg物体时一定比原长增加15cm
11.弹簧挂上物体后会伸长,测得一弹簧的长度(cm)与所挂的物体的质量(kg)间有下面的关系:
0 1 2 3 4 5
10 10.5 11 11.5 12 12.5
下列说法不正确的是( )
A.与都是变量,且是自变量,是因变量
B.所挂物体质量为4kg时,弹簧长度为12cm
C.弹簧不挂重物时的长度为0cm
D.与之间的关系式为
12.小邢到单位附近的加油站加油.如图所示的是小邢所用的加油机上的数据显示牌,则数据中的变量是( )
A.金额 B.数量 C.单价 D.金额和数量
二、填空题
13.一个蓄水池有水,打开放水闸门匀速放水,水池中的水量和放水时间的关系如表:
放水时间(min) 1 2 3 4 …
水池中水量() 48 46 44 42 …
则放水14min时,水池中有水 .
14.某商店在开学季,书包薄利多销的促销活动.原价为元,随着不同幅度的降价,日销量(单位:件)发生相应的变化:从表中可以看出,每降价元,日销量增加 件.
降价(元)
日销量(件)
15.声音在空气中传播的速度y(单位:)与气温x(单位:)的关系如下表:
气温 0 5 10 15 20
声速 331 334 337 340 343
照此规律可以发现,当气温为 时,声速达到.
16.科学家认为二氧化碳的释放量越来越多是全球变暖的原因之一.下表1950-2020年全球排放的二氧化碳量:
年份 1950 1960 1970 1980 1990 2000 2010 2020
全球排放量/百万吨 6002 9475 14989 19287 22588 24688 34180 35962
其中因变量为 .
17.变量x,y的一些对应值如表:
x … -2 -1 0 1 2 3 …
y … -8 -1 0 1 8 27 …
根据表格中的数据规律,当时,y的值是 .
三、解答题
18.我国首辆火星车正式被命名为“祝融”,为应对极限温度环境,火星车使用了新型隔温材料——纳米气凝胶,该材料的导热率与温度的关系如下表:
T 100 150 200 250 300 350
K 0.15 0.20 0.25 0.35
(1)补全表格;
(2)在这个过程中,哪个是自变量,哪个是因变量?
(3)当该材料导热率为时,温度为多少?
19.某弹簧的自然长度为3 cm,在弹性限度内,所挂物体的质量x每增加1 kg,弹簧长度y增加0.5 cm.
(1)计算所挂物体的质量分别为1 kg、2 kg、3 kg、4 kg、5 kg时的弹簧长度,并填入下表:
x/kg 0 1 2 3 4 5
y/cm 3
(2)你能写出x与y之间的关系式吗?
20.从高处抛下一个物体,测定高度与落地时间的关系如下表:
高度 5 10 15 20 25
落地时间 1 2
估计从处抛下,需多少时间落地?
21.某电影院地面的一部分观影席座位分布是扇形,其每排座位数按下列规律设置:
排数 1 2 3 4 5 6 …
座位数 60 64 68 72 76 ______ …
(1)请将表格补充完整;
(2)根据表格中的数据,请说明座位数是随排数的增长而怎样变化的?
(3)当排数是7时,该排的座位数是多少?
22.小华粉刷他的卧室共花去10小时,他记录的完成工作量的百分数如下:
时间(小时) 1 2 3 4 5 6 7 8 9 10
完成的百分数 5 25 35 50 50 65 70 80 95 100
(1)5小时他完成工作量的百分数是______;
(2)小华在______时间里工作量最大;
(3)如果小华在早晨8时开始工作,则他在______时间没有工作.
23.心理学研究发现,学生对概念的接受能力y与提出概念所用的时间x(分钟)之间有如下关系:
x 2 5 7 10 12 13 14 17 20 …
y 47.8 53.5 56.3 59 59.8 59.9 59.8 58.3 55 …
根据以上信息,回答下列问题:
(1)上表反映的两个变量中,自变量是__________,因变量是__________.
(2)当提出概念所用的时间为7分钟时,学生的接受能力是多少?
(3)在上表中,当提出概念所用的时间为多少分钟时,学生的接受能力最强?
(4)根据表中数据,说说当提出概念所用的时间在2~20分钟时,学生对概念的接受能力是怎样变化的?
24.在烧开水时,水温达到就会沸腾(标准大气压下),下表是某同学做“观察水的沸腾”实验时记录的数据:
时间 0 2 4 6 8 10 12 14 …
水的温度 30 44 58 72 86 100 100 100 …
(1)如表反映了哪两个量之间的关系?哪个是自变量?哪个是因变量?
(2)水的温度是如何随着时间的变化而变化的?
(3)时间每增加,水的温度如何变化?
(4)为了节约能源,你认为应在什么时间停止烧水?
《9.3用表格表示变量之间的关系》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B D D D D A D D A D
题号 11 12
答案 C D
1.B
【分析】根据表格数据,自变量x所挂物体的重量与因变量y弹簧的长度的关系,依次判断正误即可.
【详解】解:根据条件,可列关系式为:.
A、在没挂物体时,弹簧的长度为,根据图表,当质量时,,故此选项正确,不符合题意;
B、反映了所挂物体的质量和弹簧的长度之间的关系,所挂物体的质量是自变量;弹簧的长度是因变量,故此选项错误,符合题意;
C、在弹簧能承受的范围内,所挂物体的质量每增加,弹簧的长度就增加,故此选项正确,不符合题意;
D、由关系式,,解得,在弹簧的弹性范围内,故此选项正确,不符合题意;
故选:B.
【点睛】此题考查了函数关系式,主要考查了函数的定义和结合几何图形列函数关系式.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
2.D
【分析】本题考查变量与常量,解答本题的关键要明确:变化的量叫变量,恒定不变的量叫常量.
根据变化的量叫变量,恒定不变的量叫常量逐个判断即可得到答案.
【详解】解:由题意可得,金额单价数量,单价不变,数量与金额是变化的量,
∴单价常量,数量与金额是变量,
故选:D.
3.D
【分析】根据变量与常量,用表格表示变量之间的关系,结合表格中数据的变化规律逐项进行判断即可.
【详解】解:A.x与y都是变量,且x是自变量,y是因变量,是正确的,因此该选项不符合题意;
B.弹簧不挂重物时的长度,即当时y的值,此时,是正确的,因此该选项不符合题意;
C.物体质量x每增加,弹簧长度增加,是正确的,因此该选项不符合题意;
D.根据物体质量x每增加,弹簧长度增加,可得出所挂物体质量为时,弹簧长度为,原选项错误,因此该选项符合题意;
故选:D.
【点睛】本题考查常量与变量,用表格表示变量之间的关系,理解和发现表格中数据的变化规律是解决问题的关键.
4.D
【分析】本题考查了用表格表示变量间的关系,观察表格获得有效信息是解题的关键.
通过分析表格数据,理解变量之间的关系以及随着自变量的变化因变量的变化趋势,即可得出答案.
【详解】解:A.当时,,故选项错误;
B.h每增加,减小的值不一定,故选项错误;
C.随着h逐渐升高,t逐渐变小,故选项错误;
D. 随着h逐渐升高,小车下滑的时间逐渐变小,小车下滑的平均速度逐渐加快,故选项正确;
故选:.
5.D
【分析】本题考查函数的表示方法,找到变量之间的变化规律是解题的关键.由表格可知,增加,增加,据此列方程并求解即可.
【详解】解:由表格可知,增加,增加,则,
解得,
当为时,对应的时间为.
故选:D
6.A
【分析】此题考查的是函数的表示方法,观察表格中的数据发现:销售额是销售数量的倍,据此列出函数关系式;
【详解】解:表格中的数据发现:销售额是销售数量的倍,
∴销售额与销量的函数关系式为
故选:A.
7.D
【分析】根据用电量与应缴电费之间成正比例关系逐项判断即可.
【详解】解:A、用电量是自变量,应缴电费是因变量,故本选项叙述正确,不符合题意;
B、若用电量每增加千瓦 时,则电费增加元,故本选项叙述正确,不符合题意;
C、若用电量为5千瓦 时,则应缴电费元,故本选项叙述正确,不符合题意;
D、若小明的应缴电费比小红多元,则小明的用电量比小红的用电量多千瓦·时,故本选项叙述错误,符合题意.
故选:D.
【点睛】本题考查了用表格表示变量之间的关系,列表法能具体的反映自变量与因变量的数值对应关系.
8.D
【分析】本题考查用表格表示变量之间的关系,从表格中获取信息,逐一进行分析即可.
【详解】解:A.∵在这个变化中,自变量是温度,因变量是声速,∴说法正确,不符合题意;
B.∵根据表中数据,可得温度越低,声速越慢,∴说法正确,不符合题意;
C.∵,,,,,
∴当温度每升高,声速增加,∴说法正确,不符合题意;
D.∵,
∴当空气温度为时,声音可以传播,∴说法错误,符合题意.
故选:D.
9.A
【分析】依据题意,通过水池中的水量和放水时间的关系表,分析出水池中水量每分钟减少,从而可得函数关系式,最后可求出当放水时水池中的水量.
【详解】解:由题意知,水池中水量每分钟减少,
设水池中剩余水量为,放水时间为
∴,
∴当时,.
即当放水时,水池中有水.
故选:A.
【点睛】本题主要考查了函数的表示方法,需要通过读懂题意,识别函数关系式是解题的关键.
10.D
【分析】弹簧长度随所挂物体的重量的变化而变化,由表格数据可知物体每增加,弹簧长度就增加,可以计算当所挂物体为或时弹簧的长度,但应注意弹簧的最大长度为.
【详解】解:A.因为弹簧长度随所挂物体的重量的变化而变化,所以是自变量,是因变量.故本选项正确,不符合题意;
B.当所挂物体为时,弹簧的长度为.故本选项正确,不符合题意;
C.从表格数据中分析可知,物体每增加,弹簧长度就增加.故本选项正确,不符合题意;
D.当所挂物体为时,弹簧长度为.故本选项不正确,符合题意.
故选:D
【点睛】本题考查了变量、自变量、因变量的概念,认真审题能从题目中抽取出有效信息是解题的关键.
11.C
【分析】根据挂重物与弹簧伸长的长度,可得答案.
【详解】解:A、x和y都是变量,且x是自变量,y是因变量,故A正确;
B、当时,,故B正确;
C、当时,,故C错误;
D、由挂重物与弹簧伸长的长度,得,故D正确;
故选:C.
【点睛】本题考查了函数关系式,利用挂重物与弹簧伸长的长度得出函数关系式是解题关键.
12.D
【分析】本题考查了常量与变量,掌握相关定义是解题关键.在一个变化的过程中,数值发生变化的量称为变量,数值始终不变的量称为常量,据此即可作答.
【详解】解:数据中的变量是金额和数量,
故选:D.
13.22
【分析】根据表格中“放水时间”与“水池中水量”之间的变化规律可得答案.
【详解】解:由表格中“放水时间”与“水池中水量”对应值的变化规律可知,
放水时间每增加1min,水池中水量就减少2,
所以当放水时间为14min时,水池中水量为48﹣2×(14﹣1)=22(),
故答案为:22.
【点睛】本题考查用表格表示变量间的关系,掌握表格中两个变量的变化规律是解决问题的关键.
14.30
【分析】本题考查了变量与常量,根据表格得到变量间的关系即可.
【详解】解:由表格可知,每降价元,日销量增加(件),
故答案为:30.
15.
【分析】本题考查了利用表格表示变量之间的关系.观察图表数据,气温每升高,声速增加,然后结合当气温为,音速增加,从而可得答案.
【详解】解:∵气温每升高,音速增加,
当气温为,音速增加,
∴当声音在空气中的传播速度为,气温是,
故答案为:.
16.二氧化碳的释放量
【分析】根据自变量、因变量的定义分别得出即可;
【详解】解:由表可知,二氧化碳的释放量随着年份的增加而增大.
∴因变量为二氧化碳的释放量;
故答案为:二氧化碳的释放量;
【点睛】此题主要考查了自变量、因变量的定义,解题的关键是熟记定义进行判断.
17.-125
【分析】根据表格中两个变量对应值的变化规律得出答案.
【详解】解:由表格中两个变量对应值的变化规律可知,y=x3,
当x=﹣5时,y=(﹣5)3=﹣125,
故答案为:﹣125.
【点睛】本题考查了用表格表示变量间的关系,发现表格中两个变量对应值的变化规律是解题的关键.
18.(1)见解析
(2)温度是自变量,导热率是因变量
(3)
【分析】本题考查了函数的表示法,观察表格得出温度每增加,导热率增加是解答本题的关键.
(1)根据导热率变化规律计算即可;
(2)根据导热率随着温度的变化而变化即可解答;
(3)根据度每增加,导热率增加求解即可.
【详解】(1)观察表格可知温度每增加,导热率增加,
,
,
T 100 150 200 250 300 350
K 0.15 0.20 0.25 0.30 0.35 0.40
(2)∵导热率随着温度的变化而变化,
∴温度是自变量,导热率是因变量;
(3).
19.(1)3.5;4;4.5;5;5.5
(2)y=3+0.5x
【详解】试题分析:(1)据填表即可;
(2)利用表格中数据分析得出即可;
试题解析:(1)
(2)y=0.5x+3.
20.估计从处抛下,需落地
【分析】本题主要考查了函数关系是以及函数的表示方法等知识,学会观察表格是解决本题的关键.根据下落高度与时间进行估算即可.
【详解】解:由表格可知,从到,落地时间的增加量为,
所以从到,落地时间的增加量应小于,
即时的落地时间应在到之间.
故估计从处抛下,需落地.
21.(1)80
(2)座位数随排数的增长而增长
(3)84
【分析】本题考查用表格表示变量间的关系,找到数据的变化规律是解题的关键.
(1)由表格可知,当排数每增加1排时,座位数就会增加4,据此作答即可;
(2)根据表格中的数据,可得出座位数是随排数的增长的变化情况;
(3)根据表格中的规律,计算出当排数是7时,该排的座位数.
【详解】(1)由表格可知,当排数每增加1排时,座位数就会增加4,
当排数为6排时,座位数为80.
故答案为:80;
(2)根据表格中的数据,可得出座位数随排数的增长而增长.
(3),
答:当排数是7时,该排的座位数是84.
22.(1)
(2)第二小时
(3)时
【分析】本题考查了函数的表示方法,比较简单,阅读图表数据,准确获取信息是解题的关键.
(1)根据图表数据解答即可;
(2)根据数据找出完成百分数最多的时间即可;
(3)根据完成的百分数,开始工作后4到5小时没有工作,然后求出相应的时间即可.
【详解】(1)5小时他完成工作量的百分数是;
故答案为:;
(2)由图表可知,在第二小时完成的百分数最大是,所以,在第二小时时间里工作量最大;
故答案为:第二小时;
(3)开始工作小时工作量都是没有发生变化,
早晨8时开始工作,
在时时间没有工作.
故答案为:时.
23.(1)提出概念所用的时间x;学生对概念的接受能力y
(2)56.3
(3)13分钟
(4)见解析
【分析】此题主要考查了用表格表示变量间的关系,正确利用表格中数据得出结论是解题关键.
(1)利用表格中数据得出答案;
(2)利用表格中数据得出答案;
(3)利用表格中数据得出答案;
(4)先根据表格可知:当时,y的值最大是59.9,当时,y随x的增大而增大,当时,y随x的增大而减小,从而得出答案.
【详解】(1)解:上表反映的两个变量中,自变量是提出概念所用的时间x,因变量是学生对概念的接受能力y.
故答案为:提出概念所用的时间x;学生对概念的接受能力y
(2)解:观察表格可知,当时,,
∴当提出概念所用的时间为7分钟时,学生的接受能力是56.3.
(3)解:∵当时,y的值最大是59.9,
∴当提出概念所用的时间为13分钟时,学生的接受能力最强.
(4)解:当时,学生的接受能力y随提出概念所用的时间x的增加而增大;
当时,学生的接受能力y随提出概念所用的时间x的增加而减小.
24.(1)反映了水的温度与时间的关系,时间是自变量,水的温度是因变量
(2)水的温度随着时间的增加而增加,到时恒定
(3)时间每增加,水的温度增加,到时恒定
(4)为了节约能源,应在后停止烧水
【分析】本题主要考查了常量与变量,根据表格中数据分别分析得出是解题关键.
(1)在函数中,给一个变量x一个值,另一个变量y就有对应的值,则x是自变量,y是因变量,据此即可判断;
(2)根据表格中数据得出水的温度变化即可;
(3)根据表格中数据得出水的温度变化即可;
(4)根据表格中数据得出答案即可.
【详解】(1)解:反映了水的温度与时间的关系,时间是自变量,水的温度是因变量,
答:反映了水的温度与时间的关系,时间是自变量,水的温度是因变量;
(2)解:水的温度随着时间的增加而增加,到时恒定,
答:水的温度随着时间的增加而增加,到时恒定;
(3)解:时间每增加,水的温度增加,到时恒定,
答:时间每增加,水的温度增加,到时恒定
(4)解:为了节约能源,应在10分钟后停止烧水,
答:为了节约能源,应在10分钟后停止烧水.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
