9.4 用图像表示变量之间的关系 同步练习(含解析)
文档属性
| 名称 | 9.4 用图像表示变量之间的关系 同步练习(含解析) | 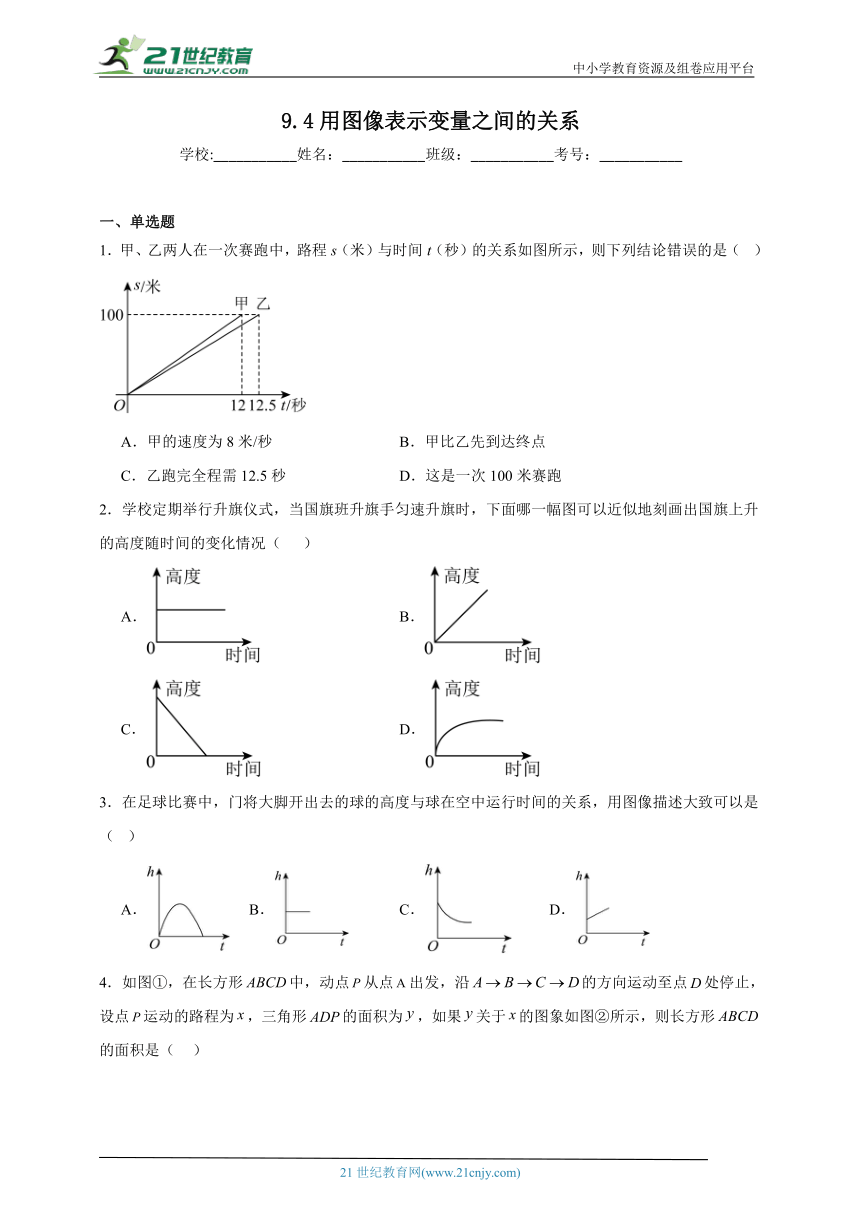 | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-03 06:01:44 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
9.4用图像表示变量之间的关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.甲、乙两人在一次赛跑中,路程s(米)与时间t(秒)的关系如图所示,则下列结论错误的是( )
A.甲的速度为8米/秒 B.甲比乙先到达终点
C.乙跑完全程需12.5秒 D.这是一次100米赛跑
2.学校定期举行升旗仪式,当国旗班升旗手匀速升旗时,下面哪一幅图可以近似地刻画出国旗上升的高度随时间的变化情况( )
A. B.
C. D.
3.在足球比赛中,门将大脚开出去的球的高度与球在空中运行时间的关系,用图像描述大致可以是( )
A. B. C. D.
4.如图①,在长方形中,动点从点出发,沿的方向运动至点处停止,设点运动的路程为,三角形的面积为,如果关于的图象如图②所示,则长方形的面积是( )
A. B. C. D.
5.甲、乙两车沿同一条路从地出发匀速行驶至相距的地,甲出发1小时后乙再出发,如图表示甲、乙两车离开地的距离与乙出发的时间之间的关系,下列结论错误的是( )
A.甲车的速度是 B.乙车的速度是
C.的值为60,的值为4 D.甲车出发后被乙车追上
6.如图,一只兔子和一只小狗从同一地点出发.下面说法正确的是( )
A.小狗的速度始终比兔子快
B.整个过程中,小狗和兔子的平均速度相同
C.在前3秒内,小狗比兔子跑得快
7.圆圆出门散步,从家出发走了到达高家的广场,看到大家正在跳舞,也加入了其中,度过了愉快的后,再用回到家中.下面图象能表示圆圆离家距离与外出时间之间关系的是( )
A. B.
C. D.
8.如图是反映两个变量的关系图,下面的四个实际情况中,哪个比较适合这幅图?( )
A.在罚球点上被踢出的球的速度与时间之间的关系
B.一杯开水放在桌上,它的水温与时间的关系
C.匀速行驶的汽车所走的路程与时间的关系
D.一架战斗机正以的速度匀速飞行,它飞行的速度与时间的关系
9.4个高度相同的容器,以相同的流速向这四个容器中注水,能正确反映容器中水的高度变化的是( ).
A. B. C. D.
10.往如图所示的容器中注水,下面图象中哪一个图象可以大致刻画容器中水的高度与时间的关系( )
A. B. C. D.
11.在足球比赛中,门将大脚开出去的球的高度与球在空中运行时间的关系,用图象描述大致可以是( )
A. B.
C. D.
12.小明从家骑自行车上学,先以0.4千米/分的速度匀速骑行5分钟,途经超市时,买文具用了5分钟,为按时到校,再以0.5千米/分的速度骑行2分钟到学校.设小明骑自行车的速度为v(千米/分),离家路程为s(千米),上学时间为t(分).下列图象能表达这一过程的是( )
A. B. C. D.
二、填空题
13.某车间的甲、乙两名工人分别同时生产同一种零件,每天完成规定工作量后即停止生产.开工两小时后,甲停下升级设备,乙每小时生产零件个数增加4个,他们一天生产零件的个数y与生产时间t(时)的关系如图所示,根据图象,下列结论正确的是 (填序号).①乙升级设备用了2小时;②一天中甲乙生产量最多相差6个;③图中的,;③甲比乙提前1小时完成工作.
14.如图所示是关于变量x,y的程序计算,若开始输入自变量x的值为3,则最后输出因变量y的值为 .
15.甲、乙两人同时骑自行车前往A地,他们距A地的路程与行驶时间之间的关系如图所示.甲乙的速度和为 .
16.小明和小华是同班同学,也是邻居,某日早晨,小明7:00先出发去学校,走了一段路后,在途中停下来吃了早饭,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公交车到了学校.如图是他们从家到学校已走的路程和小明所用时间的关系图,则下列说法中正确的是 .①小明吃早饭用时;②小华到学校的平均速度是;③小明跑步的平均速度是;④小华到学校的时间是7:05.
17.如图1,点P从的顶点B出发,沿匀速运动到点A,图2是点P运动时,线段的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则边上的高长为 .
三、解答题
18.周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时候达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园,如图是他们离家路程与小明离家时间的关系图,请根据图回答下列问题:
(1)图中自变量是____________,因变量是____________;
(2)小明家到滨海公园的路程为______________km;
(3)小明从家出发____________小时后爸爸驾车出发,爸爸驾车经过_____________小时追上小明.
19.一家快递公司的收费标准如图.用t表示邮件的质量,p表示每件快递费,n表示快递邮件的件数.
(1)填写下表.
t(千克) 3 6 10 11 12.5 13
p(元)
(2)在投寄快递邮件的事项中,t,p,n是常量,还是变量?若,投寄n件邮件的快递费记为w,此时t,p,n,w中哪些是常量?哪些是变量?
20.如图所示,分别表示了香蕉、苹果的总价与数量之间的关系,看图回答问题.
(1)香蕉的总价和数量成______比例关系;(填“正”或“反”)
(2)从图象上看,单价更贵一些的水果是______;
(3)买x千克苹果要用______元,y元可以买_____千克香蕉.
21.延安,中国五大革命圣地之一.2021年4月10日,成都和延安两地之间首次开行直达动车组列车(动车),比之前开行的普速列车(普列)缩短了不少时间,某天一辆普列从延安出发匀速驶向成都,同时另一辆动车从成都出发匀速驶向延安,两车与成都的距离(千米)与行驶时间t(时)之间的关系如表格和图像所示.
t 0 2 4 5 …
1080 930 780 705 …
(1)延安与成都的距离为_____________千米,普列到达成都所用时间为____________小时.
(2)求动车从成都到延安的距离与t之间的关系式.
(3)在成都、延安两地之间有一条隧道,当动车经过这条隧道时,两车相距135千米,求延安与这条隧道之间的距离.(隧道长度不计算在内)
22.在“看图说故事”数学学习活动中,某学习小组结合图象设计了一个问题情境
已知小明的家、超市、图书馆依次在同一条直线上,小明家离超市,超市离图书馆.小明从家出发,匀速步行到超市,在超市停留分钟后,匀速步行到达图书馆,在图书馆停留了,然后骑行返回家.给出的图象反映了这个过程中小明离家的距离与离家的时间之间的对应关系.
请根据相关信息,解答下列问题:
(1)根据图中数据填写下表:
小明离家的时间
小明离家的距离
(2)求小明从超市到图书馆的步行速度和从图书馆到家得骑行速度
23.新成药业集团研究开发了一种新药,在实验药效时发现,如果儿童按规定剂量服用,那么2时的时候血液中含药量最高,接着逐步衰减,每毫升血液中含药量(微克)随时间(时)的变化如图所示,当儿童按规定剂量服药后:
(1)何时血液中含药量最高?是多少微克?
(2)点表示什么意义?
(3)每毫升血液中含药量为2微克以上时在治疗疾病时是有效的,那么这个有效期是多长?
24.甲骑自行车以20千米/时从地去地,乙骑摩托车从地去地,同时出发,匀速行驶,各自到达终点后停止,甲、乙两人之间的距离为(千米)与甲行驶的时间为(小时)之间的关系如图所示.
(1)、两地之间的路程为 千米;
(2)从点、点、点三个点中选择一个填在横线上:表示甲到达终点的是点 ;表示乙到达终点的是点 ;表示甲、乙相遇的是点 .
(3)求乙的速度和值;
(4)求甲出发多长时间后,甲、乙两人相距30千米.
《9.4用图像表示变量之间的关系》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A B A C D B A D D B
题号 11 12
答案 A D
1.A
【分析】利用图象可得出,甲,乙的速度,以及所行路程等,注意利用所给数据结合图形逐个分析.
【详解】解:结合图象可知:s=100m,甲比乙先到达终点,乙跑完全程需12.5秒,
故B、C、D说法正确;
甲的速度是100÷12≈8.3(米/秒),故A说法不正确;
故选:A.
【点睛】此题考查了利用图象得出正确信息,解题的关键是能从图中获取相应的信息.
2.B
【分析】本题考查了用图象表示的变量间关系,根据题意明确因变量随自变量变化的趋势是解题的关键.利用用图象表示变量间关系的方法解答即可.
【详解】解:∵升旗手匀速升旗,
∴高度h将随时间t的增大而均匀增大,
∴用上升趋势的直线型表示,
∴只有B符合题意,
故选:B.
3.A
【分析】本题考查了用图象表示变量之间的关系,解题关键是了解两个变量之间的关系,解决此类题目还应有一定的生活经验.由题意可知,踢出去的足球先上向上运动,到达最高点后向下运动,据此即可判断出答案.
【详解】解:门将大脚开出去的球,踢出去的足球先上向上运动,到达最高点后向下运动,
即高度h先越来越大,再越来越小,
故选:A.
4.C
【分析】本题考查了用图象法表示两个变量的关系,根据图象结合图形得出,,即可得出长方形的面积,采用数形结合的思想是解此题的关键.
【详解】解:由图形可得,当点在上时,的面积逐渐增大,当点在上时,的面积不变,结合图象可得,,
∴长方形的面积是,
故选:C.
5.D
【分析】根据图象,列出关于a,b的方程,求出a,b的值,从而即可逐一判断各个选项.
【详解】解:根据图象可知,(300-a)÷b=(240-a)÷3=a÷1,
解得:a=60,b=4,
甲车的速度=60÷1=60km/h,乙车的速度=300÷3=100km/h,
故A,B,C正确,不符合题意;
∵60÷(100-60)=1.5,1.5+1=2.5h,
∴甲车出发后被乙车追上,
故D错误,符合题意,
故选D.
【点睛】本题考查了用图像表示的变量间关系,理解图象以及分别求出甲、乙两人的速度是解题的关键.
6.B
【分析】由图可知:在前3秒内,小狗比兔子跑得慢,即可判定A、C,根据小狗与兔子同时出发,同时到达,即可判定B.
【详解】解:由图可知:在前3秒内,小狗比兔子跑得慢,故A、C错误;
由图可知:小狗与兔子同时出发,8分钟时都跑了8米,
故整个过程中,小狗和兔子的平均速度相同,故B正确,
故选:B.
【点睛】本题考查了利用图象解决问题,从图象中获取相关信息是解决本题的关键.
7.A
【分析】本题考查图象法表示实际问题的变量关系,根据题意,结合选项逐项判断即可得到答案,数形结合是解决问题的关键.
【详解】解:根据题意圆圆出门散步,从家出发走了到达高家的广场,随着时间增加,圆圆离家距离在增加;
圆圆看到大家跳舞看了,圆圆离家距离在不变;
圆圆再用回到家中,圆圆离家距离在减小;
综上所述,能表示圆圆离家距离与外出时间之间关系的图象是
故选:A.
8.D
【分析】本题主要考查了两个变量的关系图,熟练掌握变量之间的关系是解题关键.
图像中有一个物理量始终保持不变,不会因为另一个量的变化而变化.
【详解】解:A.踢出的球的速度是随着时间的增加而减少的,故A不符合题意;
B.开水的水温先是随时间的增加而减少的,最后保持不变,故B不符合题意;
C.汽车在匀速行驶中,速度保持不变,即路程与时间成正比,故C不符合题意;
D.飞速飞行的战斗机的速度始终保持不变,不会随时间的变化而变化,故D符合题意;
故选D.
9.D
【分析】本题主要考查了折线统计图,根据容器的形状,判断出水面升高的高度随时间变化的规律,逐项进行判断即可.
【详解】解:AC.因为水流速度相同,A选项中容器的底面积较小,C选项中容器的底面积较大,所以向A容器中注水时,高度随时间变化的较快,向A容器中注水时,高度随时间变化的较慢,故AC错误;
B.因为容器越向上横截面积越小,所以高度随时间变化的越来越快,故B错误;
D.因为容器越向上横截面积越大,所以高度随时间变化的越来越慢,故D正确.
故选:D.
10.B
【分析】本题考查了用图象表示变量间的关系,根据容器的形状特点对容器中水的高度与时间的关系进行分析是解题的关键.
根据容器“上大下小”的形状特点对容器中水的高度与时间的关系进行分析即可得出答案.
【详解】解:容器下端较小,上端较大,当均匀地注入水时,刚开始时高度变化较大,随着时间的推移,高度的变化速度开始减小,即高度变化越来越不明显,四个图象中只有选项符合该特点,
故选:.
11.A
【分析】本题考查了用图象表示变量之间的关系,解题关键是了解两个变量之间的关系,解决此类题目还应有一定的生活经验.由题意可知,踢出去的足球先上向上运动,到达最高点后向下运动,据此即可判断出答案.
【详解】解:门将大脚开出去的球,踢出去的足球先上向上运动,到达最高点后向下运动,
即高度h先越来越大,再越来越小,
故选:A.
12.D
【分析】根据路程、速度与时间的关系以及函数图象的特点,结合题意逐项判断解答即可.
【详解】解:由题意,小明先以0.4千米/分的速度匀速骑行5分钟,路程从0 开始随时间匀速增加到2千米;
途经超市时,买文具用了5分钟,路程不变;
再以0.5千米/分的速度骑行2分钟到学校,离家路程随时间匀速增加到3千米.
故选:D.
【点睛】本题考查用图象表示变量间关系,理解题意,能判断出路程与时间的关系是解答的关键,注意买文具时路程不变.
13.②④/④②
【分析】本题主要考查了用图象表示两个变量的关系,根据图象即可判断①;求出升级设备前后甲的生产速度,以及2小时前后乙的生产速度,进而确定a、b、c的值,再分别求出对应时间段甲乙生产量最多相差的个数即可判断②③;求出乙需要的总时间即可判断④,进而可得结论.
【详解】解:甲升级设备用了小时,乙没有升级设备,故①说法错误;
由图象可知,当时,甲每小时生产个,乙每小时生产个,
∴当,且时,甲乙生产量最多相差个;
当时,乙每小时生产个,则当时,甲乙生产量最多相差个;
甲升级完成后每天生产个,
当时,由于甲比乙每小时生产得多,故当,甲乙生产量最多相差个,不符合题意;
当时,由于甲比乙每小时生产得多,故当时,甲乙生产量最多个;
综上所述,一天中甲乙生产量最多相差6个,故②正确;
∵,
∴,故③错误;
,,
∴甲比乙提前1小时完成工作,故④说法正确;
∴说法正确的有②④,
故答案为:②④.
14.30
【分析】本题考查了求代数式的值,正确理解程序计算的流程是解题的关键.先将代入,求得的值为6,小于20,根据程序流程,将再次代入,求得的值为30,大于20,即可输出结果.
【详解】当时,,
当时,,
所以.
故答案为:30.
15.
【分析】本题考查了用图象表示变量间的关系,根据图象求得甲、乙的速度是解题的关键.根据图象,利用速度等于路程除以时间,分别求出甲乙的速度即可得解.
【详解】解:根据图可知,甲距离A地,行驶时间为,乙距离A地,行驶时间为,
甲的速度为,乙的速度为,
甲乙的速度和为.
故答案为:
16.①②③
【分析】观察图像,根据路程、速度、时间之间的关系依次判断即可.
【详解】由图知小明从家出发,第8分钟至第13分钟在吃早饭,因此小明吃早饭用了5分钟,故①正确;
由图知小华从家到学校的路程为1200米,用时分钟,因此小华到学校的速度为,故②正确;
由图知小明从第13分钟至第20分钟跑步到学校,用时分钟,跑的路程为米,因此小明跑步的速度为,故③正确;
由图知小华到学校的时间为7:13,故④错误.
故答案为:①②③
【点睛】本题主要考查了用图像法表示变量之间的关系,读懂题意,能从所给图像中获取信息是解题的关键.
17.4
【分析】根据题意,当点P从B运动到A的过程中,由0开始增大,到C时最大为5;当点P从C运动到A的过程中,的长度先减小,当时达到最小,最小值为4,然后又增大,进而可求解.
【详解】解:根据题意,结合图1和图2,
当点P从B运动到A的过程中,由0开始增大,到C时,最大为5;当点P从C运动到A的过程中,的长度先减小,当时达到最小,最小值为4,然后又开始增大,则边上的高长为4,
故答案为:4.
【点睛】本题考查图象的理解和应用,把图形和图象结合理解得到线段长度的变化是解答的关键.
18.(1)时间t; 离家路程s
(2)30
(3)2.5;
【分析】(1)根据图象进行判断,即可得出自变量与因变量;
(2)根据图象中数据即可得到路程;
(3)根据图象直接可得到爸爸驾车出发的时间;先算出小明坐公交车到滨海公园的平均速度和爸爸驾车的平均速度,设爸爸出发后xh追上小明,根据在x这段时间内,爸爸通过的路程比小明乘公交车通过的路程多12km列出方程,解方程即可.
【详解】(1)由图可得,自变量是时间t,因变量是离家路程s;
故答案为:时间t;离家的路程s.
(2)由图可得,小明家到滨海公园的路程为30km;
故答案为:30.
(3)由图可得,小明出发2.5小时后爸爸驾车出发;
爸爸驾车的平均速度为,
小明乘公交车的平均速度为:,
设爸爸出发后xh追上小明,根据题意得:
,解得:.
故答案为:2.5;h.
【点睛】本题考查了路程时间的图象,以及行程问题的数量关系的运用,解答时理解清楚图象的意义是解答此题的关键.
19.(1)见解析
(2)t,p,n都是变量.若,则p为常量,t,n,w均为变量
【分析】(1)根据图填空即可
(2)根据变量和常量的定义:在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量可得x、y是变量.
【详解】(1)如表.
t(千克) 3 6 10 11 12.5 13
p(元) 6 6 6 7 9 9
(2)在投寄快递邮件的事项中,t,p,n都是变量.若,则p为常量,t,n,w均为变量.
【点睛】本题主要考查了函数图象以及常量和变量,在解题时要根据常量和变量的定义进行解答是本题的关键.
20.(1)正
(2)香蕉
(3)4x,
【分析】此题考查了正比例和反比例的判断,并从图中获取数据,进行计算.
(1)正比例:如果两种相关联的量中相对应的两个数的比值一定,这两种量就叫做成正比例的量.它们的关系叫做正比例关系;反比例:如果两个变量的乘积为常数时的比例关系,一方发生变化,其另一方随之起相反的变化,就是反比例.
(2)从图中获得数据,香蕉的单价高于苹果的单价.
(3)单价数量总价,总价单价数量,代入即可.
【详解】(1)从图中可以看出,香蕉的总价和购买的数量成正比例;
(2)从图象上看,单价更贵一些的水果是香蕉;
(3)从图象上看,买1千克苹果要用4元,买1千克香蕉要用8元,
买x千克苹果要用元,y元可以买千克香蕉;
故答案为:,.
21.(1),
(2)
(3)延安与这条隧道之间的距离为450千米或270千米
【分析】(1)根据表格中的数据可得到延安与成都的距离和普快的速度,进而可求解;
(2)根据图像先求得动车的速度,再根据路程=速度×时间求得与t之间的关系式即可;
(3)分普快在延安和隧道之间和普快在隧道和成都之间两种情况,根据题意列方程求解即可.
【详解】(1)解:根据题意和表格数据可知,延安与成都的距离为千米,
普快的速度为(千米/时),
普快到达成都所用时间为(小时),
故答案为:,;
(2)解:由图像知,动车的速度为(千米/时),
∴与t之间的关系式为;
(3)解:当普快在延安和隧道之间时,
根据题意,得,
解得,
则延安与这条隧道之间的距离为(千米);
当普快在隧道和成都之间时,
根据题意,得,
解得,
延安与这条隧道之间的距离为(千米),
综上,延安与这条隧道之间的距离为450千米或270千米.
【点睛】本题考查变量之间的关系、一元一次方程的应用,理解题意,正确求得关系式,运用分类讨论思想求解是解答的关键.
22.(1),,,,,
(2)小明从超市到图书馆步行的速度为,从图书馆到家骑行的速度为
【分析】本题考查了函数图像及其信息,分类思想,运动与函数的关系,熟练掌握函数图像及其信息,分类思想是解题的关键.
(1)根据运动时间,结合运动过程,停留超市,去图书馆,停留图书馆,计算即可,
(2)根据路程、速度、时间之间的关系求解即可.
【详解】(1)解:根据题意,当时,速度为,
∴小明离家的时间时,小明离家的距离,
∵小明离家的时间时,停留在超市,
∴小明离家的时间时,小明离家的距离,
当时,运动速度为,
∴小明离家的时间时,小明离家的距离,
小明离家的时间时,小明离家的距离,
当时,停留在图书馆,
∴小明离家的时间时,小明离家的距离,
当时,运动速度为,
∴小明离家的时间时,小明离家的距离,
故答案为:,,,,,;
(2)解:从超市到图书馆,步行的时间为,路程为,
∴,步行的速度为();
从图书馆到家,骑行的时间为,骑行的路程为,
∴骑行的速度为();
答:小明从超市到图书馆步行的速度为,从图书馆到家骑行的速度为.
23.(1)服药后2时;4微克
(2)服药后10时,每毫升血液中不含此药
(3)5小时
【分析】本题考查用图象表示变量之间的关系,解题的关键在于根据图象获取需要的信息求解.
(1)根据图中信息回答即可;
(2) 根据图中信息回答即可;
(3)服药后每毫升血液中含药量达到2微克的时间是1时,衰减到2微克的时间是6时,据此计算出有效时间即可.
【详解】(1)解:由图可知,服药后2时血液中含药量最高,是4微克;
(2)解:点表示当时间为10时,每毫升血液中含药量为0微克,即服药后10时,每毫升血液中不含此药;
(3)解:由图知,这个有效期为(时),
这个有效期为5小时.
24.(1)120
(2);;
(3)乙的速度是(千米/时),
(4)甲出发1.5小时或2.5小时后,甲、乙两人相距30千米
【分析】本题考查用图象表示变量之间的关系,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
(1)由图象可得,A、B两地之间路程为120千米;
(2)根据图象中的数据可以解答本题;
(3)根据图象知,根据相遇时间为2小时可得乙的速度,根据路程除以速度可求出乙行完全程所用时间;
(4)分相遇前相距30千米和相遇后相距30千米,列方程求解即可
【详解】(1)解:根据函数图象可得,A、B两地之间路程为120千米,
故答案为:120;
(2)解:表示甲到达终点的是点P;表示乙到达终点的是点N;表示甲、乙相遇的是点M,
故答案为: P;N ; M;
(3)解:乙的速度是:(千米/时);
,
(4)解:相遇之前:,
解得,
相遇之后:,
解得,
即甲出发1.5小时或2.5小时后,甲、乙两人相距30千米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
9.4用图像表示变量之间的关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.甲、乙两人在一次赛跑中,路程s(米)与时间t(秒)的关系如图所示,则下列结论错误的是( )
A.甲的速度为8米/秒 B.甲比乙先到达终点
C.乙跑完全程需12.5秒 D.这是一次100米赛跑
2.学校定期举行升旗仪式,当国旗班升旗手匀速升旗时,下面哪一幅图可以近似地刻画出国旗上升的高度随时间的变化情况( )
A. B.
C. D.
3.在足球比赛中,门将大脚开出去的球的高度与球在空中运行时间的关系,用图像描述大致可以是( )
A. B. C. D.
4.如图①,在长方形中,动点从点出发,沿的方向运动至点处停止,设点运动的路程为,三角形的面积为,如果关于的图象如图②所示,则长方形的面积是( )
A. B. C. D.
5.甲、乙两车沿同一条路从地出发匀速行驶至相距的地,甲出发1小时后乙再出发,如图表示甲、乙两车离开地的距离与乙出发的时间之间的关系,下列结论错误的是( )
A.甲车的速度是 B.乙车的速度是
C.的值为60,的值为4 D.甲车出发后被乙车追上
6.如图,一只兔子和一只小狗从同一地点出发.下面说法正确的是( )
A.小狗的速度始终比兔子快
B.整个过程中,小狗和兔子的平均速度相同
C.在前3秒内,小狗比兔子跑得快
7.圆圆出门散步,从家出发走了到达高家的广场,看到大家正在跳舞,也加入了其中,度过了愉快的后,再用回到家中.下面图象能表示圆圆离家距离与外出时间之间关系的是( )
A. B.
C. D.
8.如图是反映两个变量的关系图,下面的四个实际情况中,哪个比较适合这幅图?( )
A.在罚球点上被踢出的球的速度与时间之间的关系
B.一杯开水放在桌上,它的水温与时间的关系
C.匀速行驶的汽车所走的路程与时间的关系
D.一架战斗机正以的速度匀速飞行,它飞行的速度与时间的关系
9.4个高度相同的容器,以相同的流速向这四个容器中注水,能正确反映容器中水的高度变化的是( ).
A. B. C. D.
10.往如图所示的容器中注水,下面图象中哪一个图象可以大致刻画容器中水的高度与时间的关系( )
A. B. C. D.
11.在足球比赛中,门将大脚开出去的球的高度与球在空中运行时间的关系,用图象描述大致可以是( )
A. B.
C. D.
12.小明从家骑自行车上学,先以0.4千米/分的速度匀速骑行5分钟,途经超市时,买文具用了5分钟,为按时到校,再以0.5千米/分的速度骑行2分钟到学校.设小明骑自行车的速度为v(千米/分),离家路程为s(千米),上学时间为t(分).下列图象能表达这一过程的是( )
A. B. C. D.
二、填空题
13.某车间的甲、乙两名工人分别同时生产同一种零件,每天完成规定工作量后即停止生产.开工两小时后,甲停下升级设备,乙每小时生产零件个数增加4个,他们一天生产零件的个数y与生产时间t(时)的关系如图所示,根据图象,下列结论正确的是 (填序号).①乙升级设备用了2小时;②一天中甲乙生产量最多相差6个;③图中的,;③甲比乙提前1小时完成工作.
14.如图所示是关于变量x,y的程序计算,若开始输入自变量x的值为3,则最后输出因变量y的值为 .
15.甲、乙两人同时骑自行车前往A地,他们距A地的路程与行驶时间之间的关系如图所示.甲乙的速度和为 .
16.小明和小华是同班同学,也是邻居,某日早晨,小明7:00先出发去学校,走了一段路后,在途中停下来吃了早饭,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公交车到了学校.如图是他们从家到学校已走的路程和小明所用时间的关系图,则下列说法中正确的是 .①小明吃早饭用时;②小华到学校的平均速度是;③小明跑步的平均速度是;④小华到学校的时间是7:05.
17.如图1,点P从的顶点B出发,沿匀速运动到点A,图2是点P运动时,线段的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则边上的高长为 .
三、解答题
18.周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时候达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园,如图是他们离家路程与小明离家时间的关系图,请根据图回答下列问题:
(1)图中自变量是____________,因变量是____________;
(2)小明家到滨海公园的路程为______________km;
(3)小明从家出发____________小时后爸爸驾车出发,爸爸驾车经过_____________小时追上小明.
19.一家快递公司的收费标准如图.用t表示邮件的质量,p表示每件快递费,n表示快递邮件的件数.
(1)填写下表.
t(千克) 3 6 10 11 12.5 13
p(元)
(2)在投寄快递邮件的事项中,t,p,n是常量,还是变量?若,投寄n件邮件的快递费记为w,此时t,p,n,w中哪些是常量?哪些是变量?
20.如图所示,分别表示了香蕉、苹果的总价与数量之间的关系,看图回答问题.
(1)香蕉的总价和数量成______比例关系;(填“正”或“反”)
(2)从图象上看,单价更贵一些的水果是______;
(3)买x千克苹果要用______元,y元可以买_____千克香蕉.
21.延安,中国五大革命圣地之一.2021年4月10日,成都和延安两地之间首次开行直达动车组列车(动车),比之前开行的普速列车(普列)缩短了不少时间,某天一辆普列从延安出发匀速驶向成都,同时另一辆动车从成都出发匀速驶向延安,两车与成都的距离(千米)与行驶时间t(时)之间的关系如表格和图像所示.
t 0 2 4 5 …
1080 930 780 705 …
(1)延安与成都的距离为_____________千米,普列到达成都所用时间为____________小时.
(2)求动车从成都到延安的距离与t之间的关系式.
(3)在成都、延安两地之间有一条隧道,当动车经过这条隧道时,两车相距135千米,求延安与这条隧道之间的距离.(隧道长度不计算在内)
22.在“看图说故事”数学学习活动中,某学习小组结合图象设计了一个问题情境
已知小明的家、超市、图书馆依次在同一条直线上,小明家离超市,超市离图书馆.小明从家出发,匀速步行到超市,在超市停留分钟后,匀速步行到达图书馆,在图书馆停留了,然后骑行返回家.给出的图象反映了这个过程中小明离家的距离与离家的时间之间的对应关系.
请根据相关信息,解答下列问题:
(1)根据图中数据填写下表:
小明离家的时间
小明离家的距离
(2)求小明从超市到图书馆的步行速度和从图书馆到家得骑行速度
23.新成药业集团研究开发了一种新药,在实验药效时发现,如果儿童按规定剂量服用,那么2时的时候血液中含药量最高,接着逐步衰减,每毫升血液中含药量(微克)随时间(时)的变化如图所示,当儿童按规定剂量服药后:
(1)何时血液中含药量最高?是多少微克?
(2)点表示什么意义?
(3)每毫升血液中含药量为2微克以上时在治疗疾病时是有效的,那么这个有效期是多长?
24.甲骑自行车以20千米/时从地去地,乙骑摩托车从地去地,同时出发,匀速行驶,各自到达终点后停止,甲、乙两人之间的距离为(千米)与甲行驶的时间为(小时)之间的关系如图所示.
(1)、两地之间的路程为 千米;
(2)从点、点、点三个点中选择一个填在横线上:表示甲到达终点的是点 ;表示乙到达终点的是点 ;表示甲、乙相遇的是点 .
(3)求乙的速度和值;
(4)求甲出发多长时间后,甲、乙两人相距30千米.
《9.4用图像表示变量之间的关系》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A B A C D B A D D B
题号 11 12
答案 A D
1.A
【分析】利用图象可得出,甲,乙的速度,以及所行路程等,注意利用所给数据结合图形逐个分析.
【详解】解:结合图象可知:s=100m,甲比乙先到达终点,乙跑完全程需12.5秒,
故B、C、D说法正确;
甲的速度是100÷12≈8.3(米/秒),故A说法不正确;
故选:A.
【点睛】此题考查了利用图象得出正确信息,解题的关键是能从图中获取相应的信息.
2.B
【分析】本题考查了用图象表示的变量间关系,根据题意明确因变量随自变量变化的趋势是解题的关键.利用用图象表示变量间关系的方法解答即可.
【详解】解:∵升旗手匀速升旗,
∴高度h将随时间t的增大而均匀增大,
∴用上升趋势的直线型表示,
∴只有B符合题意,
故选:B.
3.A
【分析】本题考查了用图象表示变量之间的关系,解题关键是了解两个变量之间的关系,解决此类题目还应有一定的生活经验.由题意可知,踢出去的足球先上向上运动,到达最高点后向下运动,据此即可判断出答案.
【详解】解:门将大脚开出去的球,踢出去的足球先上向上运动,到达最高点后向下运动,
即高度h先越来越大,再越来越小,
故选:A.
4.C
【分析】本题考查了用图象法表示两个变量的关系,根据图象结合图形得出,,即可得出长方形的面积,采用数形结合的思想是解此题的关键.
【详解】解:由图形可得,当点在上时,的面积逐渐增大,当点在上时,的面积不变,结合图象可得,,
∴长方形的面积是,
故选:C.
5.D
【分析】根据图象,列出关于a,b的方程,求出a,b的值,从而即可逐一判断各个选项.
【详解】解:根据图象可知,(300-a)÷b=(240-a)÷3=a÷1,
解得:a=60,b=4,
甲车的速度=60÷1=60km/h,乙车的速度=300÷3=100km/h,
故A,B,C正确,不符合题意;
∵60÷(100-60)=1.5,1.5+1=2.5h,
∴甲车出发后被乙车追上,
故D错误,符合题意,
故选D.
【点睛】本题考查了用图像表示的变量间关系,理解图象以及分别求出甲、乙两人的速度是解题的关键.
6.B
【分析】由图可知:在前3秒内,小狗比兔子跑得慢,即可判定A、C,根据小狗与兔子同时出发,同时到达,即可判定B.
【详解】解:由图可知:在前3秒内,小狗比兔子跑得慢,故A、C错误;
由图可知:小狗与兔子同时出发,8分钟时都跑了8米,
故整个过程中,小狗和兔子的平均速度相同,故B正确,
故选:B.
【点睛】本题考查了利用图象解决问题,从图象中获取相关信息是解决本题的关键.
7.A
【分析】本题考查图象法表示实际问题的变量关系,根据题意,结合选项逐项判断即可得到答案,数形结合是解决问题的关键.
【详解】解:根据题意圆圆出门散步,从家出发走了到达高家的广场,随着时间增加,圆圆离家距离在增加;
圆圆看到大家跳舞看了,圆圆离家距离在不变;
圆圆再用回到家中,圆圆离家距离在减小;
综上所述,能表示圆圆离家距离与外出时间之间关系的图象是
故选:A.
8.D
【分析】本题主要考查了两个变量的关系图,熟练掌握变量之间的关系是解题关键.
图像中有一个物理量始终保持不变,不会因为另一个量的变化而变化.
【详解】解:A.踢出的球的速度是随着时间的增加而减少的,故A不符合题意;
B.开水的水温先是随时间的增加而减少的,最后保持不变,故B不符合题意;
C.汽车在匀速行驶中,速度保持不变,即路程与时间成正比,故C不符合题意;
D.飞速飞行的战斗机的速度始终保持不变,不会随时间的变化而变化,故D符合题意;
故选D.
9.D
【分析】本题主要考查了折线统计图,根据容器的形状,判断出水面升高的高度随时间变化的规律,逐项进行判断即可.
【详解】解:AC.因为水流速度相同,A选项中容器的底面积较小,C选项中容器的底面积较大,所以向A容器中注水时,高度随时间变化的较快,向A容器中注水时,高度随时间变化的较慢,故AC错误;
B.因为容器越向上横截面积越小,所以高度随时间变化的越来越快,故B错误;
D.因为容器越向上横截面积越大,所以高度随时间变化的越来越慢,故D正确.
故选:D.
10.B
【分析】本题考查了用图象表示变量间的关系,根据容器的形状特点对容器中水的高度与时间的关系进行分析是解题的关键.
根据容器“上大下小”的形状特点对容器中水的高度与时间的关系进行分析即可得出答案.
【详解】解:容器下端较小,上端较大,当均匀地注入水时,刚开始时高度变化较大,随着时间的推移,高度的变化速度开始减小,即高度变化越来越不明显,四个图象中只有选项符合该特点,
故选:.
11.A
【分析】本题考查了用图象表示变量之间的关系,解题关键是了解两个变量之间的关系,解决此类题目还应有一定的生活经验.由题意可知,踢出去的足球先上向上运动,到达最高点后向下运动,据此即可判断出答案.
【详解】解:门将大脚开出去的球,踢出去的足球先上向上运动,到达最高点后向下运动,
即高度h先越来越大,再越来越小,
故选:A.
12.D
【分析】根据路程、速度与时间的关系以及函数图象的特点,结合题意逐项判断解答即可.
【详解】解:由题意,小明先以0.4千米/分的速度匀速骑行5分钟,路程从0 开始随时间匀速增加到2千米;
途经超市时,买文具用了5分钟,路程不变;
再以0.5千米/分的速度骑行2分钟到学校,离家路程随时间匀速增加到3千米.
故选:D.
【点睛】本题考查用图象表示变量间关系,理解题意,能判断出路程与时间的关系是解答的关键,注意买文具时路程不变.
13.②④/④②
【分析】本题主要考查了用图象表示两个变量的关系,根据图象即可判断①;求出升级设备前后甲的生产速度,以及2小时前后乙的生产速度,进而确定a、b、c的值,再分别求出对应时间段甲乙生产量最多相差的个数即可判断②③;求出乙需要的总时间即可判断④,进而可得结论.
【详解】解:甲升级设备用了小时,乙没有升级设备,故①说法错误;
由图象可知,当时,甲每小时生产个,乙每小时生产个,
∴当,且时,甲乙生产量最多相差个;
当时,乙每小时生产个,则当时,甲乙生产量最多相差个;
甲升级完成后每天生产个,
当时,由于甲比乙每小时生产得多,故当,甲乙生产量最多相差个,不符合题意;
当时,由于甲比乙每小时生产得多,故当时,甲乙生产量最多个;
综上所述,一天中甲乙生产量最多相差6个,故②正确;
∵,
∴,故③错误;
,,
∴甲比乙提前1小时完成工作,故④说法正确;
∴说法正确的有②④,
故答案为:②④.
14.30
【分析】本题考查了求代数式的值,正确理解程序计算的流程是解题的关键.先将代入,求得的值为6,小于20,根据程序流程,将再次代入,求得的值为30,大于20,即可输出结果.
【详解】当时,,
当时,,
所以.
故答案为:30.
15.
【分析】本题考查了用图象表示变量间的关系,根据图象求得甲、乙的速度是解题的关键.根据图象,利用速度等于路程除以时间,分别求出甲乙的速度即可得解.
【详解】解:根据图可知,甲距离A地,行驶时间为,乙距离A地,行驶时间为,
甲的速度为,乙的速度为,
甲乙的速度和为.
故答案为:
16.①②③
【分析】观察图像,根据路程、速度、时间之间的关系依次判断即可.
【详解】由图知小明从家出发,第8分钟至第13分钟在吃早饭,因此小明吃早饭用了5分钟,故①正确;
由图知小华从家到学校的路程为1200米,用时分钟,因此小华到学校的速度为,故②正确;
由图知小明从第13分钟至第20分钟跑步到学校,用时分钟,跑的路程为米,因此小明跑步的速度为,故③正确;
由图知小华到学校的时间为7:13,故④错误.
故答案为:①②③
【点睛】本题主要考查了用图像法表示变量之间的关系,读懂题意,能从所给图像中获取信息是解题的关键.
17.4
【分析】根据题意,当点P从B运动到A的过程中,由0开始增大,到C时最大为5;当点P从C运动到A的过程中,的长度先减小,当时达到最小,最小值为4,然后又增大,进而可求解.
【详解】解:根据题意,结合图1和图2,
当点P从B运动到A的过程中,由0开始增大,到C时,最大为5;当点P从C运动到A的过程中,的长度先减小,当时达到最小,最小值为4,然后又开始增大,则边上的高长为4,
故答案为:4.
【点睛】本题考查图象的理解和应用,把图形和图象结合理解得到线段长度的变化是解答的关键.
18.(1)时间t; 离家路程s
(2)30
(3)2.5;
【分析】(1)根据图象进行判断,即可得出自变量与因变量;
(2)根据图象中数据即可得到路程;
(3)根据图象直接可得到爸爸驾车出发的时间;先算出小明坐公交车到滨海公园的平均速度和爸爸驾车的平均速度,设爸爸出发后xh追上小明,根据在x这段时间内,爸爸通过的路程比小明乘公交车通过的路程多12km列出方程,解方程即可.
【详解】(1)由图可得,自变量是时间t,因变量是离家路程s;
故答案为:时间t;离家的路程s.
(2)由图可得,小明家到滨海公园的路程为30km;
故答案为:30.
(3)由图可得,小明出发2.5小时后爸爸驾车出发;
爸爸驾车的平均速度为,
小明乘公交车的平均速度为:,
设爸爸出发后xh追上小明,根据题意得:
,解得:.
故答案为:2.5;h.
【点睛】本题考查了路程时间的图象,以及行程问题的数量关系的运用,解答时理解清楚图象的意义是解答此题的关键.
19.(1)见解析
(2)t,p,n都是变量.若,则p为常量,t,n,w均为变量
【分析】(1)根据图填空即可
(2)根据变量和常量的定义:在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量可得x、y是变量.
【详解】(1)如表.
t(千克) 3 6 10 11 12.5 13
p(元) 6 6 6 7 9 9
(2)在投寄快递邮件的事项中,t,p,n都是变量.若,则p为常量,t,n,w均为变量.
【点睛】本题主要考查了函数图象以及常量和变量,在解题时要根据常量和变量的定义进行解答是本题的关键.
20.(1)正
(2)香蕉
(3)4x,
【分析】此题考查了正比例和反比例的判断,并从图中获取数据,进行计算.
(1)正比例:如果两种相关联的量中相对应的两个数的比值一定,这两种量就叫做成正比例的量.它们的关系叫做正比例关系;反比例:如果两个变量的乘积为常数时的比例关系,一方发生变化,其另一方随之起相反的变化,就是反比例.
(2)从图中获得数据,香蕉的单价高于苹果的单价.
(3)单价数量总价,总价单价数量,代入即可.
【详解】(1)从图中可以看出,香蕉的总价和购买的数量成正比例;
(2)从图象上看,单价更贵一些的水果是香蕉;
(3)从图象上看,买1千克苹果要用4元,买1千克香蕉要用8元,
买x千克苹果要用元,y元可以买千克香蕉;
故答案为:,.
21.(1),
(2)
(3)延安与这条隧道之间的距离为450千米或270千米
【分析】(1)根据表格中的数据可得到延安与成都的距离和普快的速度,进而可求解;
(2)根据图像先求得动车的速度,再根据路程=速度×时间求得与t之间的关系式即可;
(3)分普快在延安和隧道之间和普快在隧道和成都之间两种情况,根据题意列方程求解即可.
【详解】(1)解:根据题意和表格数据可知,延安与成都的距离为千米,
普快的速度为(千米/时),
普快到达成都所用时间为(小时),
故答案为:,;
(2)解:由图像知,动车的速度为(千米/时),
∴与t之间的关系式为;
(3)解:当普快在延安和隧道之间时,
根据题意,得,
解得,
则延安与这条隧道之间的距离为(千米);
当普快在隧道和成都之间时,
根据题意,得,
解得,
延安与这条隧道之间的距离为(千米),
综上,延安与这条隧道之间的距离为450千米或270千米.
【点睛】本题考查变量之间的关系、一元一次方程的应用,理解题意,正确求得关系式,运用分类讨论思想求解是解答的关键.
22.(1),,,,,
(2)小明从超市到图书馆步行的速度为,从图书馆到家骑行的速度为
【分析】本题考查了函数图像及其信息,分类思想,运动与函数的关系,熟练掌握函数图像及其信息,分类思想是解题的关键.
(1)根据运动时间,结合运动过程,停留超市,去图书馆,停留图书馆,计算即可,
(2)根据路程、速度、时间之间的关系求解即可.
【详解】(1)解:根据题意,当时,速度为,
∴小明离家的时间时,小明离家的距离,
∵小明离家的时间时,停留在超市,
∴小明离家的时间时,小明离家的距离,
当时,运动速度为,
∴小明离家的时间时,小明离家的距离,
小明离家的时间时,小明离家的距离,
当时,停留在图书馆,
∴小明离家的时间时,小明离家的距离,
当时,运动速度为,
∴小明离家的时间时,小明离家的距离,
故答案为:,,,,,;
(2)解:从超市到图书馆,步行的时间为,路程为,
∴,步行的速度为();
从图书馆到家,骑行的时间为,骑行的路程为,
∴骑行的速度为();
答:小明从超市到图书馆步行的速度为,从图书馆到家骑行的速度为.
23.(1)服药后2时;4微克
(2)服药后10时,每毫升血液中不含此药
(3)5小时
【分析】本题考查用图象表示变量之间的关系,解题的关键在于根据图象获取需要的信息求解.
(1)根据图中信息回答即可;
(2) 根据图中信息回答即可;
(3)服药后每毫升血液中含药量达到2微克的时间是1时,衰减到2微克的时间是6时,据此计算出有效时间即可.
【详解】(1)解:由图可知,服药后2时血液中含药量最高,是4微克;
(2)解:点表示当时间为10时,每毫升血液中含药量为0微克,即服药后10时,每毫升血液中不含此药;
(3)解:由图知,这个有效期为(时),
这个有效期为5小时.
24.(1)120
(2);;
(3)乙的速度是(千米/时),
(4)甲出发1.5小时或2.5小时后,甲、乙两人相距30千米
【分析】本题考查用图象表示变量之间的关系,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
(1)由图象可得,A、B两地之间路程为120千米;
(2)根据图象中的数据可以解答本题;
(3)根据图象知,根据相遇时间为2小时可得乙的速度,根据路程除以速度可求出乙行完全程所用时间;
(4)分相遇前相距30千米和相遇后相距30千米,列方程求解即可
【详解】(1)解:根据函数图象可得,A、B两地之间路程为120千米,
故答案为:120;
(2)解:表示甲到达终点的是点P;表示乙到达终点的是点N;表示甲、乙相遇的是点M,
故答案为: P;N ; M;
(3)解:乙的速度是:(千米/时);
,
(4)解:相遇之前:,
解得,
相遇之后:,
解得,
即甲出发1.5小时或2.5小时后,甲、乙两人相距30千米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
