湖南省永州市祁阳市浯溪二中2024-2025学年下学期第一次月考九年级数学试卷(含答案)
文档属性
| 名称 | 湖南省永州市祁阳市浯溪二中2024-2025学年下学期第一次月考九年级数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 698.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-03 08:01:43 | ||
图片预览


文档简介
2024-2025学年祁阳市浯溪二中九年级下册第一次月考数学试卷
考试时间:120分钟 满分:120分
一.选择题(共10小题,每小题3分,满分30分,在每小题给出的四个选项中,只有一个选项符合题目要求的。)
1.下列各数中:,﹣3.14156,200%,﹣5%,﹣(+)63,﹣(﹣)0.01001,2024属于负数的有( )
A.3个 B.4个 C.5个 D.6个
2.中国海油2024年3月8日宣布,在南海珠江口盆地发现我国首个深水深层大油田——开平南油田,探明油气地质储量约1.02亿吨油当量,对于我国保障国家能源安全具有重要意义,数据“1.02亿”用科学记数法可表示为( )
A.1.2×106 B.1.02×106 C.1.2×108 D.1.02×108
3.如图是由5个相同的小正方体组成的立体图形,它的左视图是( )
A. B. C. D.
4.下列运算正确的是( )
A.x2 x3=x6 B.a6÷a2=a3 C.(a3b)2=a6b2 D.5a﹣3a=2
5.化简:的结果是( )
A. B. C. D.
6.下列命题是真命题的是( )
A.同位角相等 B.菱形的四条边相等
C.正五边形的其中一个内角是72° D.单项式的次数是4
7.如图,点A,B,C在⊙O上,∠BAC=36°,则∠BOC的大小是( )
A.72° B.54° C.36° D.18°
8.下列说法中正确的是( )
A.一组数据2,2,3,4的中位数是2
B.了解一批灯泡的使用寿命的情况,适合抽样调查
C.小明的三次数学成绩分别是106分、110分、116分,则小明这三次成绩的平均数是111
D.某日最高气温是7℃,最低气温是﹣2℃,则该日的温差是5℃
9.如图,点D,E,F分别是△ABC三边上的中点,若△ABC的面积为12,则△DEF的面积为( )
A.3 B.4 C.6 D.8
10.在平面直角坐标系xOy中,对于点P(x,y),若x,y均为整数,则称点P为“整点”,特别地,当(其中xy≠0)的值为整数时,称“整点”P为“超整点”.已知点P(2a﹣4,a+3)在第二象限,下列说法正确的有( )
①a<﹣3;②若点P为“整点”,则点P的个数为4个;③若点P为“超整点”,则点P的个数为1个;④若点P为“超整点”,则点P到两坐标轴的距离之和大于10.
A.1个 B.2个 C.3个 D.4个
题号 1 2 3 4 5 6 7 8 9 10
答案
二.填空题(共8小题,每小题3分,满分24分)
11.如果数x与﹣20互为相反数,那么x等于 .
12.为开展“学习二十大,奋进新征程”主题宣讲活动,某学校从甲、乙、丙三位宣讲员中随机抽取两人参加,恰好选中甲、丙两人的概率为 .
13.方程的解是 .
14.若等腰三角形有一个内角为40°,则它的顶角度数为 .
15.若关于x的方程3x2﹣4x﹣k=0无解,则k的取值范围为 .
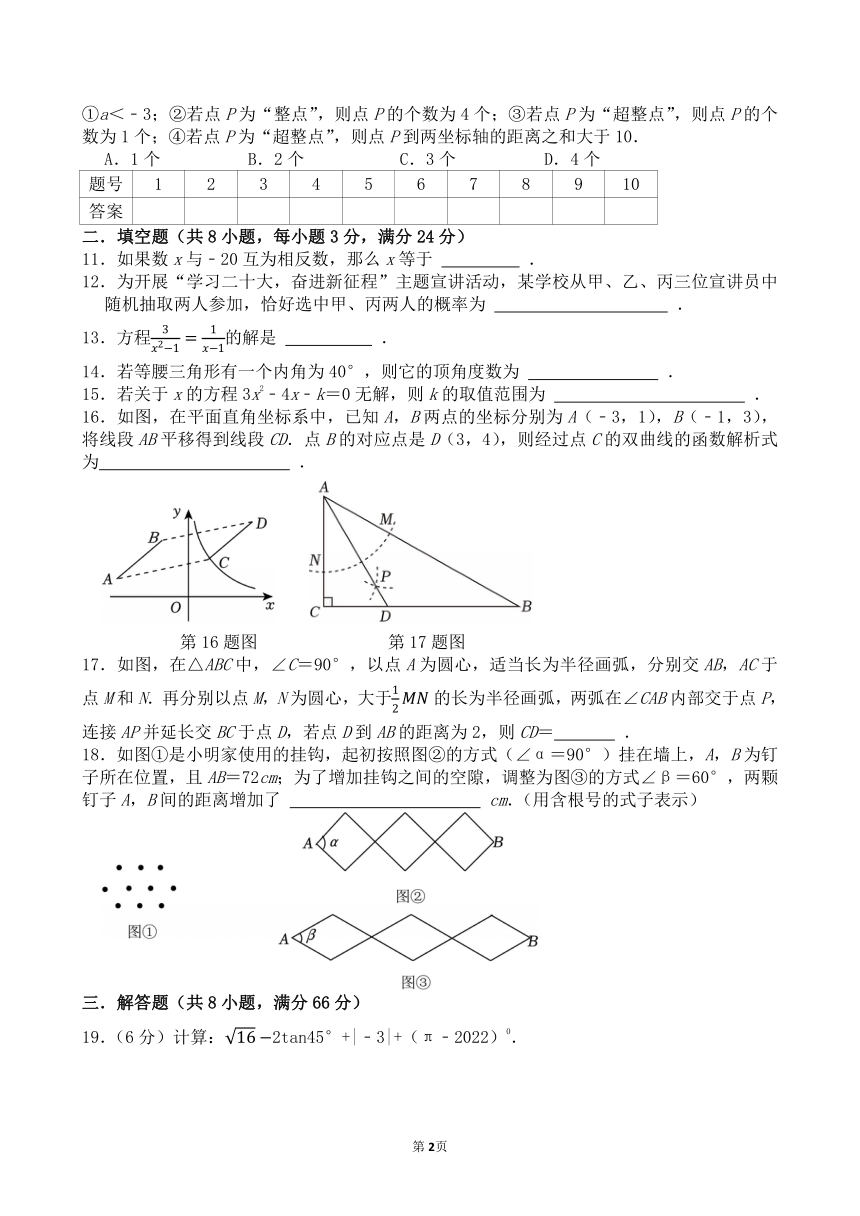
16.如图,在平面直角坐标系中,已知A,B两点的坐标分别为A(﹣3,1),B(﹣1,3),将线段AB平移得到线段CD.点B的对应点是D(3,4),则经过点C的双曲线的函数解析式为 .
第16题图 第17题图
17.如图,在△ABC中,∠C=90°,以点A为圆心,适当长为半径画弧,分别交AB,AC于点M和N.再分别以点M,N为圆心,大于的长为半径画弧,两弧在∠CAB内部交于点P,连接AP并延长交BC于点D,若点D到AB的距离为2,则CD= .
18.如图①是小明家使用的挂钩,起初按照图②的方式(∠α=90°)挂在墙上,A,B为钉子所在位置,且AB=72cm;为了增加挂钩之间的空隙,调整为图③的方式∠β=60°,两颗钉子A,B间的距离增加了 cm.(用含根号的式子表示)
三.解答题(共8小题,满分66分)
19.(6分)计算:2tan45°+|﹣3|+(π﹣2022)0.
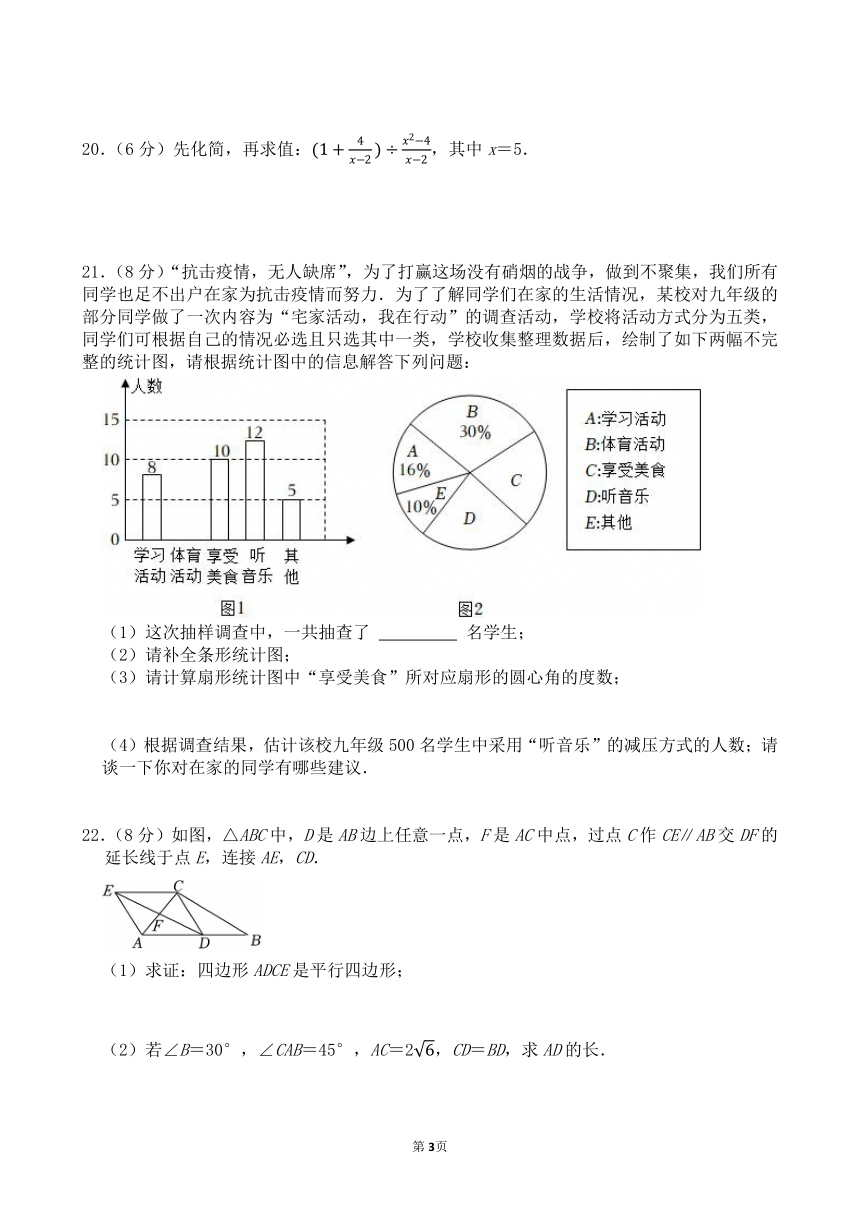
20.(6分)先化简,再求值:,其中x=5.
21.(8分)“抗击疫情,无人缺席”,为了打赢这场没有硝烟的战争,做到不聚集,我们所有同学也足不出户在家为抗击疫情而努力.为了了解同学们在家的生活情况,某校对九年级的部分同学做了一次内容为“宅家活动,我在行动”的调查活动,学校将活动方式分为五类,同学们可根据自己的情况必选且只选其中一类,学校收集整理数据后,绘制了如下两幅不完整的统计图,请根据统计图中的信息解答下列问题:
(1)这次抽样调查中,一共抽查了 名学生;
(2)请补全条形统计图;
(3)请计算扇形统计图中“享受美食”所对应扇形的圆心角的度数;
(4)根据调查结果,估计该校九年级500名学生中采用“听音乐”的减压方式的人数;请谈一下你对在家的同学有哪些建议.
22.(8分)如图,△ABC中,D是AB边上任意一点,F是AC中点,过点C作CE∥AB交DF的延长线于点E,连接AE,CD.
(1)求证:四边形ADCE是平行四边形;
(2)若∠B=30°,∠CAB=45°,AC=2,CD=BD,求AD的长.
23.(9分)开学前夕,某书店计划购进A、B两种笔记本共350本,已知A种笔记本的进价为12元/本,B种笔记本的进价为15元/本,共计4800元.
(1)请问购进了A种笔记本多少本?
(2)在销售过程中,A、B两种笔记本的标价分别为20元/本、25元/本.受疫情影响,两种笔记本按标价各卖出m本以后,该店进行促销活动,剩余的A种笔记本按标价的七折全部售出,剩余的B种笔记本按成本价清货,若两种笔记本的总利润不少于2348元,请求出m的最小值.
24.(9分)防火门是消防中的必备设备,作为隔绝烟火的关键屏障,被广泛应用于公共建筑的封闭楼梯间、安全通道、地下室、消防控制室等.图1是某栋楼层的双开防火门实物图,将其左门抽象成俯视示意图如图2和图3所示.已知墙面OM⊥ON,门宽AB=80cm.
(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32,1.73)
(1)如图2,当左门绕点A逆时针完全打开贴到墙时,点B落在点C处,此时∠ACO=18°,求OA的长.
(2)如图3,当左门绕点A逆时针打开60°时,点B落在点D处,求此时点D到墙面ON的距离.
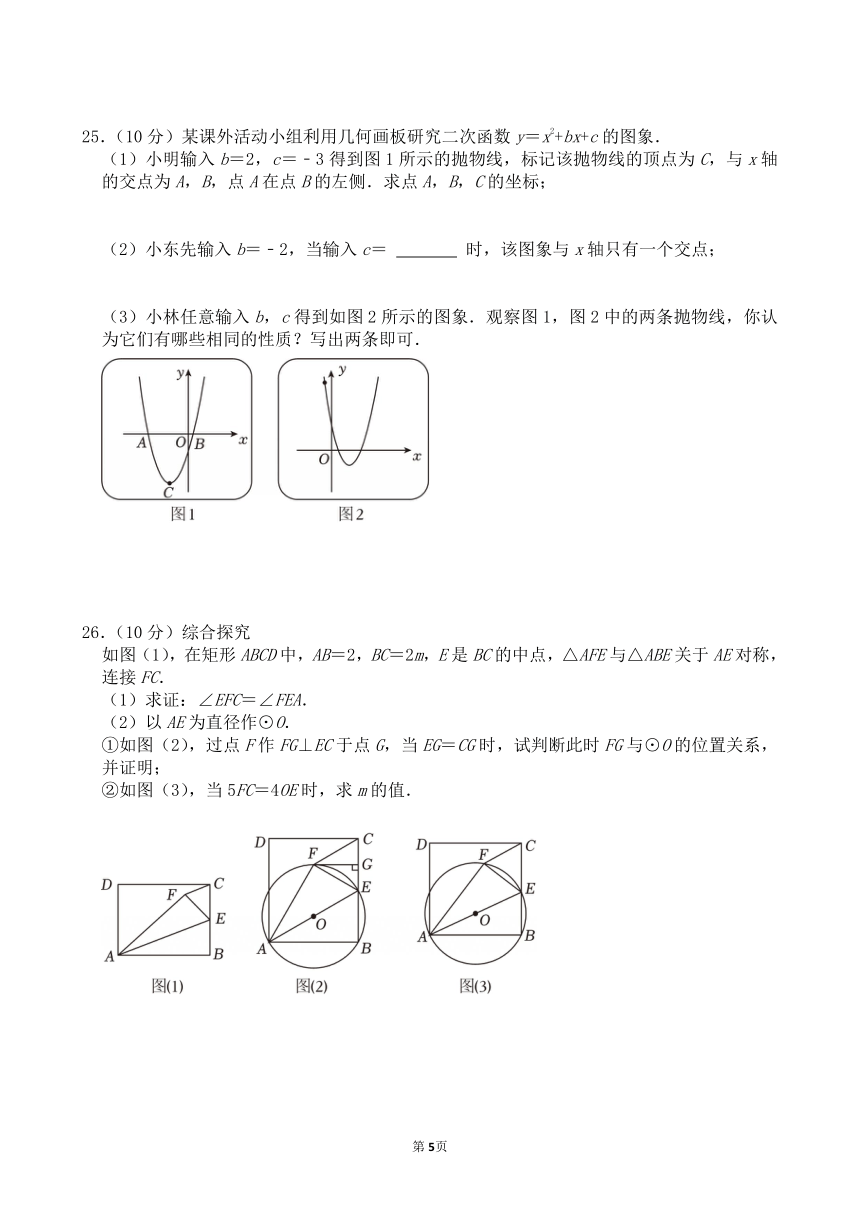
25.(10分)某课外活动小组利用几何画板研究二次函数y=x2+bx+c的图象.
(1)小明输入b=2,c=﹣3得到图1所示的抛物线,标记该抛物线的顶点为C,与x轴的交点为A,B,点A在点B的左侧.求点A,B,C的坐标;
(2)小东先输入b=﹣2,当输入c= 时,该图象与x轴只有一个交点;
(3)小林任意输入b,c得到如图2所示的图象.观察图1,图2中的两条抛物线,你认为它们有哪些相同的性质?写出两条即可.
26.(10分)综合探究
如图(1),在矩形ABCD中,AB=2,BC=2m,E是BC的中点,△AFE与△ABE关于AE对称,连接FC.
(1)求证:∠EFC=∠FEA.
(2)以AE为直径作⊙O.
①如图(2),过点F作FG⊥EC于点G,当EG=CG时,试判断此时FG与⊙O的位置关系,并证明;
②如图(3),当5FC=4OE时,求m的值.
参考答案
一.选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B D D C A B A B A B
10.解析:∵点P(2a﹣4,a+3)在第二象限,∴,∴﹣3<a<2,故①错误,不符合题意;∵点P(2a﹣4,a+3)为“整点”,﹣3<a<2,∴整数a为﹣2,﹣1,0,1,∴点P的个数为4个,故②正确,符合题意;∴“整点”P为(﹣8,1),(﹣6,2),(﹣4,3),(﹣2,4),∵,,,∴“超整点”P为(﹣2,4),故③正确,符合题意;∵点P(2a﹣4,a+3)为“超整点”,∴点P坐标为(﹣2,4),∴点P到两坐标轴的距离之和2+4=6,故④错误,不符合题意;故选:B.
11.20.12..13.x=2.14.40°或100°.15..16..解析:∵A,B两点的坐标分别为A(﹣3,1),B(﹣1,3),将线段AB平移得到线段CD.点B的对应点是D(3,4),∴向左平移了4个单位,向上平移了1个单位,∴A(﹣3,1)平移后对应的点C(1,2),∴设反比例函数解析式为,将点C(1,2)代入得,∴k=2,∴.
17.2.18.(3672)解析:当α=90°时,连接AB,此时四边形AFCE是正方形,连接AB,如图②所示,∴AB=72(cm),∴AC=72÷3=24(cm),∴AE12(cm).当β=60°时,连AB、EF,如图③所示,此时四边形AFCE是菱形,此时△AEF是等边三角形,∴AE=EF=12(cm),∴EO=6(cm),在Rt△AEO中,由勾股定理可知:AO6(cm),∴AC=2AO=12(cm),∴AB=3AC=36(cm),故调整为图③的方式∠β=60°,两颗钉子A,B间的距离增加了(3672)(cm),
19.解:原式=4﹣2×1+3+1=4﹣2+3+1=6.
20.解: ,当x=5时,原式.
21.解:(1)一共抽查的学生:8÷16%=50(名);故答案为:50;(2)参加“体育活动”的人数为:50×30%=15(名),补全统计图如图所示:
(3)“享受美食”所对应扇形的圆心角的度数为:360°72°;(4)根据题意得:
500120(人),答:估计该校九年级500名学生中采用“听音乐”来减压方式的人数有120人.
22.(1)证明:∵CE∥AB,∴∠ECF=∠DAF,∵F是AC的中点,∴AF=CF.在△AFD与△CFE中,,∴△AFD≌△CFE(ASA),∴DF=EF,∴四边形ADCE是平行四边形;
(2)解:如图,过C作CG⊥AD于G,则∠CGA=∠CGD=90°,∵∠CAB=45°,∴△ACG是等腰直角三角形,∴AG=CGAC22,∵∠B=30°,CD=BD,∴∠B=∠DCB=30°,∴∠CDG=∠B+∠DCB=60°,∴∠DCG=90°﹣∠CDG=30°,∴DGCG=2,∴AD=AG+DG=22.
23.解:(1)设购进了A种笔记本x本,购进了B种笔记本y本,由题意得:,
解得:,答:购进了A种笔记本150本,购进了B种笔记本200本;(2)由题意得:20m+25m+(150﹣m)×20×0.7+(200﹣m)×15﹣4800≥2348,解得:m≥128,
答:m的最小值为128.
24.解:(1)由题意得AC=AB=80cm,在Rt△OAC中,∠ACO=18°,AC=80cm,sin∠ACO,则OA=AC sin∠ACO≈80×0.31=24.8(cm);
(2)如图,过点D作DE⊥AB于点E,
由题意得AD=AB=80cm,在Rt△ADE中,∠DAE=60°,AD=80cm,DE=AD×∠DAE=8069.2(cm),答:点D到墙面ON的距离约为69.2cm.
25.解:(1)当b=2,c=﹣3时,二次函数的表达式为y=x2+2x﹣3=(x+1)2﹣4,∴顶点C的坐标为(﹣1,﹣4).当y=0时,x2+2x﹣3=0,解得x1=﹣3,x2=1.∵点A在点B的左侧,∴A(﹣3,0),B(1,0);(2)先输入b=﹣2,当输入c时,抛物线的表达式为:y=x2﹣2x+c,∵图象与x轴只有一个交点,则Δ=4﹣4c=0,则c=1,故答案为:1;
(3)从图象看,它们都是轴对称图形;它们的开口都朝上;它们都可以由y=x2的图象平移得到(答案不唯一).
26.(1)证明:如图,∵△AFE与△ABE关于AE对称,∴EF=EB,∠FEA=∠1,∴2∠FEA+∠2=180°,∵E是BC的中点,∴EC=EB,∴EF=EC,∴∠EFC=∠3,
∴2∠EFC+∠2=180°,∴∠EFC=∠FEA.
(2)①FG与⊙O相切,证明如下:如图,连接OF,
∵EG=CG,BE=CE,BC=2m,∴,EF=BE=m,在Rt△EFG中,,
∴∠4=30°,∴∠2=60°,∴∠1=∠3=60°,在矩形ABCD中,∠B=90°,由对称可知∠AFE=90°,∵AE是⊙O的直径,∴点F在⊙O上,∴OF=OE,∴∠5=∠3=60°,
∴∠4+∠5=90°,即OF⊥FG,∴FG 与⊙O相切.
②如图,连接OF,
∵OE=OF,∴∠OEF=∠OFE,由(1)知∠EFC=∠ECF,∠EFC=∠FEA,∴∠OEF=∠OFE=∠EFC=∠ECF,∴△OEF∽△EFC,∴,∵5FC=4OE,设FC=4x,则OE=5x,
∵,∴,∴m2=20x2,在Rt△ABE中,AB=2,BE=m,AE=2OE=10x,∴22+m2=(10x)2=100x2=5m2,∴m2=1,∴m=1(负值已舍).
第1页
考试时间:120分钟 满分:120分
一.选择题(共10小题,每小题3分,满分30分,在每小题给出的四个选项中,只有一个选项符合题目要求的。)
1.下列各数中:,﹣3.14156,200%,﹣5%,﹣(+)63,﹣(﹣)0.01001,2024属于负数的有( )
A.3个 B.4个 C.5个 D.6个
2.中国海油2024年3月8日宣布,在南海珠江口盆地发现我国首个深水深层大油田——开平南油田,探明油气地质储量约1.02亿吨油当量,对于我国保障国家能源安全具有重要意义,数据“1.02亿”用科学记数法可表示为( )
A.1.2×106 B.1.02×106 C.1.2×108 D.1.02×108
3.如图是由5个相同的小正方体组成的立体图形,它的左视图是( )
A. B. C. D.
4.下列运算正确的是( )
A.x2 x3=x6 B.a6÷a2=a3 C.(a3b)2=a6b2 D.5a﹣3a=2
5.化简:的结果是( )
A. B. C. D.
6.下列命题是真命题的是( )
A.同位角相等 B.菱形的四条边相等
C.正五边形的其中一个内角是72° D.单项式的次数是4
7.如图,点A,B,C在⊙O上,∠BAC=36°,则∠BOC的大小是( )
A.72° B.54° C.36° D.18°
8.下列说法中正确的是( )
A.一组数据2,2,3,4的中位数是2
B.了解一批灯泡的使用寿命的情况,适合抽样调查
C.小明的三次数学成绩分别是106分、110分、116分,则小明这三次成绩的平均数是111
D.某日最高气温是7℃,最低气温是﹣2℃,则该日的温差是5℃
9.如图,点D,E,F分别是△ABC三边上的中点,若△ABC的面积为12,则△DEF的面积为( )
A.3 B.4 C.6 D.8
10.在平面直角坐标系xOy中,对于点P(x,y),若x,y均为整数,则称点P为“整点”,特别地,当(其中xy≠0)的值为整数时,称“整点”P为“超整点”.已知点P(2a﹣4,a+3)在第二象限,下列说法正确的有( )
①a<﹣3;②若点P为“整点”,则点P的个数为4个;③若点P为“超整点”,则点P的个数为1个;④若点P为“超整点”,则点P到两坐标轴的距离之和大于10.
A.1个 B.2个 C.3个 D.4个
题号 1 2 3 4 5 6 7 8 9 10
答案
二.填空题(共8小题,每小题3分,满分24分)
11.如果数x与﹣20互为相反数,那么x等于 .
12.为开展“学习二十大,奋进新征程”主题宣讲活动,某学校从甲、乙、丙三位宣讲员中随机抽取两人参加,恰好选中甲、丙两人的概率为 .
13.方程的解是 .
14.若等腰三角形有一个内角为40°,则它的顶角度数为 .
15.若关于x的方程3x2﹣4x﹣k=0无解,则k的取值范围为 .
16.如图,在平面直角坐标系中,已知A,B两点的坐标分别为A(﹣3,1),B(﹣1,3),将线段AB平移得到线段CD.点B的对应点是D(3,4),则经过点C的双曲线的函数解析式为 .
第16题图 第17题图
17.如图,在△ABC中,∠C=90°,以点A为圆心,适当长为半径画弧,分别交AB,AC于点M和N.再分别以点M,N为圆心,大于的长为半径画弧,两弧在∠CAB内部交于点P,连接AP并延长交BC于点D,若点D到AB的距离为2,则CD= .
18.如图①是小明家使用的挂钩,起初按照图②的方式(∠α=90°)挂在墙上,A,B为钉子所在位置,且AB=72cm;为了增加挂钩之间的空隙,调整为图③的方式∠β=60°,两颗钉子A,B间的距离增加了 cm.(用含根号的式子表示)
三.解答题(共8小题,满分66分)
19.(6分)计算:2tan45°+|﹣3|+(π﹣2022)0.
20.(6分)先化简,再求值:,其中x=5.
21.(8分)“抗击疫情,无人缺席”,为了打赢这场没有硝烟的战争,做到不聚集,我们所有同学也足不出户在家为抗击疫情而努力.为了了解同学们在家的生活情况,某校对九年级的部分同学做了一次内容为“宅家活动,我在行动”的调查活动,学校将活动方式分为五类,同学们可根据自己的情况必选且只选其中一类,学校收集整理数据后,绘制了如下两幅不完整的统计图,请根据统计图中的信息解答下列问题:
(1)这次抽样调查中,一共抽查了 名学生;
(2)请补全条形统计图;
(3)请计算扇形统计图中“享受美食”所对应扇形的圆心角的度数;
(4)根据调查结果,估计该校九年级500名学生中采用“听音乐”的减压方式的人数;请谈一下你对在家的同学有哪些建议.
22.(8分)如图,△ABC中,D是AB边上任意一点,F是AC中点,过点C作CE∥AB交DF的延长线于点E,连接AE,CD.
(1)求证:四边形ADCE是平行四边形;
(2)若∠B=30°,∠CAB=45°,AC=2,CD=BD,求AD的长.
23.(9分)开学前夕,某书店计划购进A、B两种笔记本共350本,已知A种笔记本的进价为12元/本,B种笔记本的进价为15元/本,共计4800元.
(1)请问购进了A种笔记本多少本?
(2)在销售过程中,A、B两种笔记本的标价分别为20元/本、25元/本.受疫情影响,两种笔记本按标价各卖出m本以后,该店进行促销活动,剩余的A种笔记本按标价的七折全部售出,剩余的B种笔记本按成本价清货,若两种笔记本的总利润不少于2348元,请求出m的最小值.
24.(9分)防火门是消防中的必备设备,作为隔绝烟火的关键屏障,被广泛应用于公共建筑的封闭楼梯间、安全通道、地下室、消防控制室等.图1是某栋楼层的双开防火门实物图,将其左门抽象成俯视示意图如图2和图3所示.已知墙面OM⊥ON,门宽AB=80cm.
(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32,1.73)
(1)如图2,当左门绕点A逆时针完全打开贴到墙时,点B落在点C处,此时∠ACO=18°,求OA的长.
(2)如图3,当左门绕点A逆时针打开60°时,点B落在点D处,求此时点D到墙面ON的距离.
25.(10分)某课外活动小组利用几何画板研究二次函数y=x2+bx+c的图象.
(1)小明输入b=2,c=﹣3得到图1所示的抛物线,标记该抛物线的顶点为C,与x轴的交点为A,B,点A在点B的左侧.求点A,B,C的坐标;
(2)小东先输入b=﹣2,当输入c= 时,该图象与x轴只有一个交点;
(3)小林任意输入b,c得到如图2所示的图象.观察图1,图2中的两条抛物线,你认为它们有哪些相同的性质?写出两条即可.
26.(10分)综合探究
如图(1),在矩形ABCD中,AB=2,BC=2m,E是BC的中点,△AFE与△ABE关于AE对称,连接FC.
(1)求证:∠EFC=∠FEA.
(2)以AE为直径作⊙O.
①如图(2),过点F作FG⊥EC于点G,当EG=CG时,试判断此时FG与⊙O的位置关系,并证明;
②如图(3),当5FC=4OE时,求m的值.
参考答案
一.选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B D D C A B A B A B
10.解析:∵点P(2a﹣4,a+3)在第二象限,∴,∴﹣3<a<2,故①错误,不符合题意;∵点P(2a﹣4,a+3)为“整点”,﹣3<a<2,∴整数a为﹣2,﹣1,0,1,∴点P的个数为4个,故②正确,符合题意;∴“整点”P为(﹣8,1),(﹣6,2),(﹣4,3),(﹣2,4),∵,,,∴“超整点”P为(﹣2,4),故③正确,符合题意;∵点P(2a﹣4,a+3)为“超整点”,∴点P坐标为(﹣2,4),∴点P到两坐标轴的距离之和2+4=6,故④错误,不符合题意;故选:B.
11.20.12..13.x=2.14.40°或100°.15..16..解析:∵A,B两点的坐标分别为A(﹣3,1),B(﹣1,3),将线段AB平移得到线段CD.点B的对应点是D(3,4),∴向左平移了4个单位,向上平移了1个单位,∴A(﹣3,1)平移后对应的点C(1,2),∴设反比例函数解析式为,将点C(1,2)代入得,∴k=2,∴.
17.2.18.(3672)解析:当α=90°时,连接AB,此时四边形AFCE是正方形,连接AB,如图②所示,∴AB=72(cm),∴AC=72÷3=24(cm),∴AE12(cm).当β=60°时,连AB、EF,如图③所示,此时四边形AFCE是菱形,此时△AEF是等边三角形,∴AE=EF=12(cm),∴EO=6(cm),在Rt△AEO中,由勾股定理可知:AO6(cm),∴AC=2AO=12(cm),∴AB=3AC=36(cm),故调整为图③的方式∠β=60°,两颗钉子A,B间的距离增加了(3672)(cm),
19.解:原式=4﹣2×1+3+1=4﹣2+3+1=6.
20.解: ,当x=5时,原式.
21.解:(1)一共抽查的学生:8÷16%=50(名);故答案为:50;(2)参加“体育活动”的人数为:50×30%=15(名),补全统计图如图所示:
(3)“享受美食”所对应扇形的圆心角的度数为:360°72°;(4)根据题意得:
500120(人),答:估计该校九年级500名学生中采用“听音乐”来减压方式的人数有120人.
22.(1)证明:∵CE∥AB,∴∠ECF=∠DAF,∵F是AC的中点,∴AF=CF.在△AFD与△CFE中,,∴△AFD≌△CFE(ASA),∴DF=EF,∴四边形ADCE是平行四边形;
(2)解:如图,过C作CG⊥AD于G,则∠CGA=∠CGD=90°,∵∠CAB=45°,∴△ACG是等腰直角三角形,∴AG=CGAC22,∵∠B=30°,CD=BD,∴∠B=∠DCB=30°,∴∠CDG=∠B+∠DCB=60°,∴∠DCG=90°﹣∠CDG=30°,∴DGCG=2,∴AD=AG+DG=22.
23.解:(1)设购进了A种笔记本x本,购进了B种笔记本y本,由题意得:,
解得:,答:购进了A种笔记本150本,购进了B种笔记本200本;(2)由题意得:20m+25m+(150﹣m)×20×0.7+(200﹣m)×15﹣4800≥2348,解得:m≥128,
答:m的最小值为128.
24.解:(1)由题意得AC=AB=80cm,在Rt△OAC中,∠ACO=18°,AC=80cm,sin∠ACO,则OA=AC sin∠ACO≈80×0.31=24.8(cm);
(2)如图,过点D作DE⊥AB于点E,
由题意得AD=AB=80cm,在Rt△ADE中,∠DAE=60°,AD=80cm,DE=AD×∠DAE=8069.2(cm),答:点D到墙面ON的距离约为69.2cm.
25.解:(1)当b=2,c=﹣3时,二次函数的表达式为y=x2+2x﹣3=(x+1)2﹣4,∴顶点C的坐标为(﹣1,﹣4).当y=0时,x2+2x﹣3=0,解得x1=﹣3,x2=1.∵点A在点B的左侧,∴A(﹣3,0),B(1,0);(2)先输入b=﹣2,当输入c时,抛物线的表达式为:y=x2﹣2x+c,∵图象与x轴只有一个交点,则Δ=4﹣4c=0,则c=1,故答案为:1;
(3)从图象看,它们都是轴对称图形;它们的开口都朝上;它们都可以由y=x2的图象平移得到(答案不唯一).
26.(1)证明:如图,∵△AFE与△ABE关于AE对称,∴EF=EB,∠FEA=∠1,∴2∠FEA+∠2=180°,∵E是BC的中点,∴EC=EB,∴EF=EC,∴∠EFC=∠3,
∴2∠EFC+∠2=180°,∴∠EFC=∠FEA.
(2)①FG与⊙O相切,证明如下:如图,连接OF,
∵EG=CG,BE=CE,BC=2m,∴,EF=BE=m,在Rt△EFG中,,
∴∠4=30°,∴∠2=60°,∴∠1=∠3=60°,在矩形ABCD中,∠B=90°,由对称可知∠AFE=90°,∵AE是⊙O的直径,∴点F在⊙O上,∴OF=OE,∴∠5=∠3=60°,
∴∠4+∠5=90°,即OF⊥FG,∴FG 与⊙O相切.
②如图,连接OF,
∵OE=OF,∴∠OEF=∠OFE,由(1)知∠EFC=∠ECF,∠EFC=∠FEA,∴∠OEF=∠OFE=∠EFC=∠ECF,∴△OEF∽△EFC,∴,∵5FC=4OE,设FC=4x,则OE=5x,
∵,∴,∴m2=20x2,在Rt△ABE中,AB=2,BE=m,AE=2OE=10x,∴22+m2=(10x)2=100x2=5m2,∴m2=1,∴m=1(负值已舍).
第1页
同课章节目录
