第17章勾股定理检测卷(含解析)
图片预览

文档简介
中小学教育资源及组卷应用平台
第17章勾股定理检测卷-2024-2025学年数学八年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、单选题
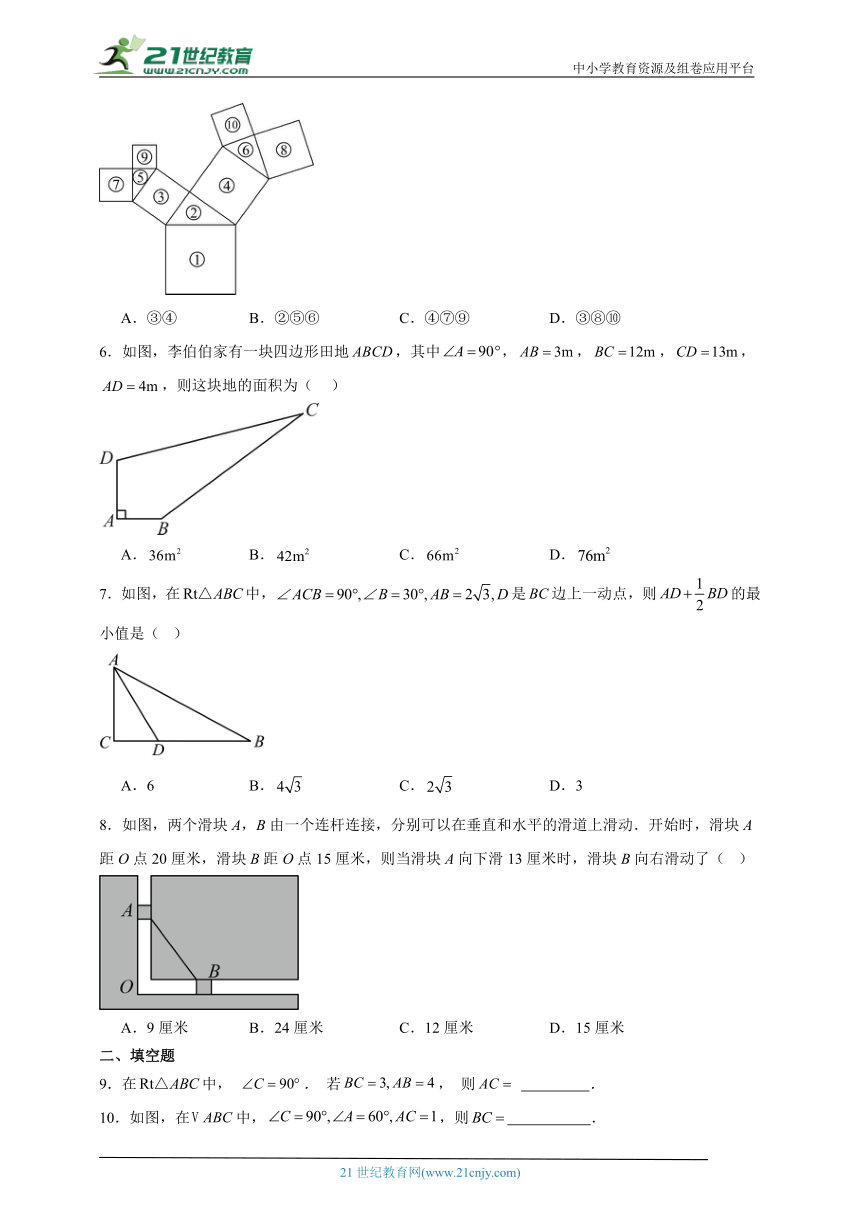
1.以下列各数为边长,能构成直角三角形的是( )
A.1,1, B.1, 4, C.3,4,6 D.1,3,3
2.如图,在边长为的小正方形网格中,位置如图所示,则点到线段的距离为( )
A. B. C. D.
3.如图,在平面直角坐标系中,点,点,以点A为圆心,以的长为半径画弧,交x正半轴于点C,则点C的坐标为( )
A. B. C. D.
4.如图,在中,有一点P在BC边上移动,若,则AP的最小值为( )
A.6 B.8 C.10 D.12
5.如图所示的所有四边形都是正方形,所有三角形都是直角三角形,在图中找出若干个图形,使得它们的面积之和恰好等于最大正方形①的面积,下列给出的方案中不正确的是( )
A.③④ B.②⑤⑥ C.④⑦⑨ D.③⑧⑩
6.如图,李伯伯家有一块四边形田地,其中,,,,,则这块地的面积为( )
A. B. C. D.
7.如图,在中,是边上一动点,则的最小值是( )
A.6 B. C. D.3
8.如图,两个滑块A,B由一个连杆连接,分别可以在垂直和水平的滑道上滑动.开始时,滑块A距O点20厘米,滑块B距O点15厘米,则当滑块A向下滑13厘米时,滑块B向右滑动了( )
A.9厘米 B.24厘米 C.12厘米 D.15厘米
二、填空题
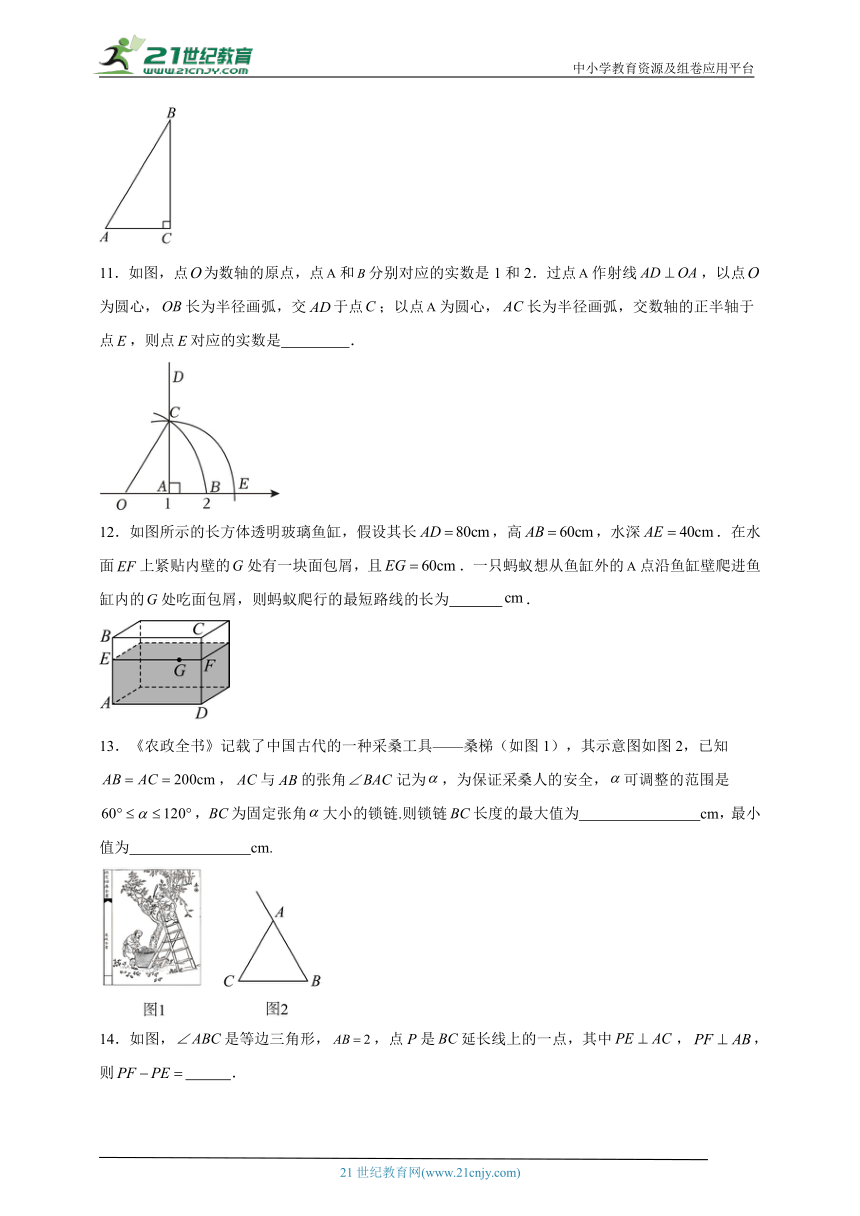
9.在中, . 若, 则 .
10.如图,在中,,则 .
11.如图,点为数轴的原点,点和分别对应的实数是1和2.过点作射线,以点为圆心,长为半径画弧,交于点;以点为圆心,长为半径画弧,交数轴的正半轴于点,则点对应的实数是 .
12.如图所示的长方体透明玻璃鱼缸,假设其长,高,水深.在水面上紧贴内壁的处有一块面包屑,且.一只蚂蚁想从鱼缸外的点沿鱼缸壁爬进鱼缸内的处吃面包屑,则蚂蚁爬行的最短路线的长为 .
13.《农政全书》记载了中国古代的一种采桑工具——桑梯(如图1),其示意图如图2,已知,与的张角记为,为保证采桑人的安全,可调整的范围是,为固定张角大小的锁链.则锁链长度的最大值为 cm,最小值为 cm.
14.如图,是等边三角形,,点P是延长线上的一点,其中,,则 .
三、解答题
15.已知三角形的三边满足.试判定三角形的形状,并求其面积.
16.如图,正方形网格中的,若小方格边长为1.
(1)求的三边长.
(2)判断是否为直角三角形.
(3)求最长边上的高.
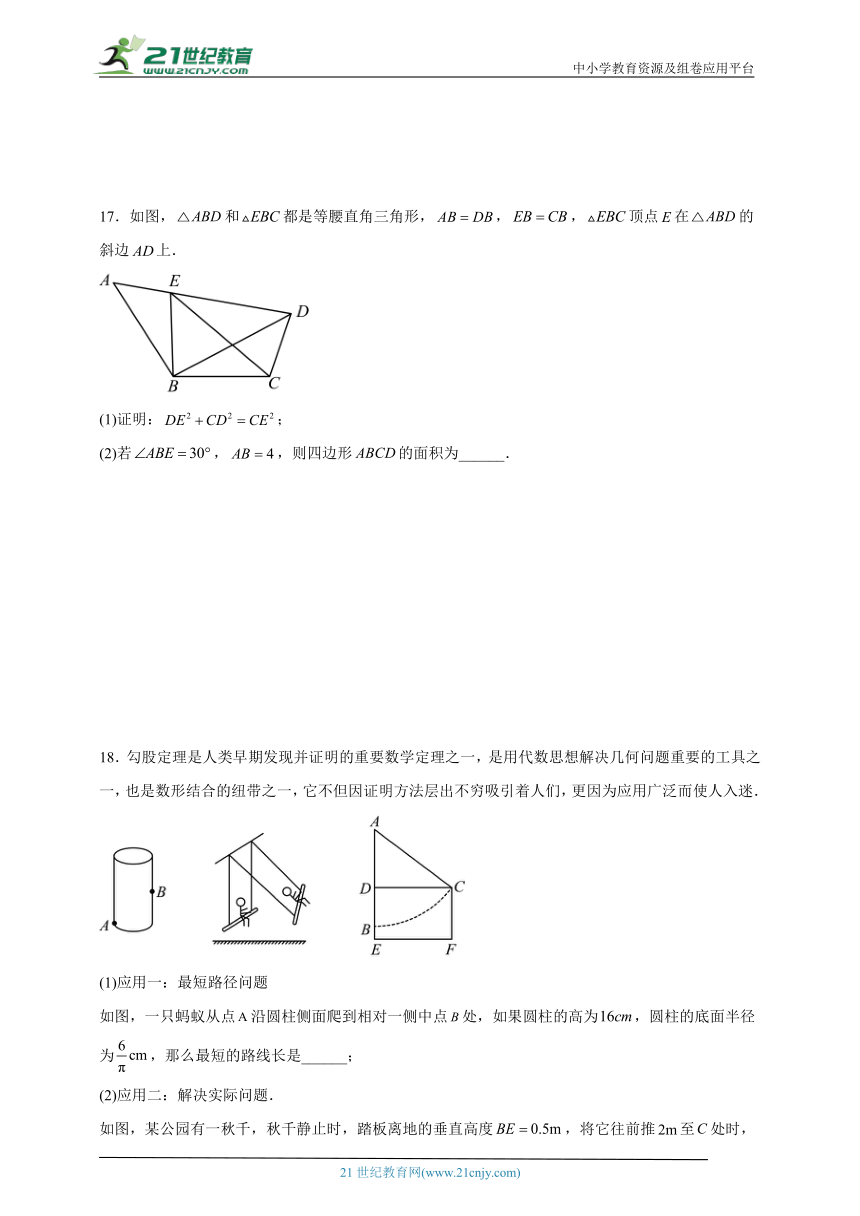
17.如图,和都是等腰直角三角形,,,顶点在的斜边上.
(1)证明:;
(2)若,,则四边形的面积为______.
18.勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题重要的工具之一,也是数形结合的纽带之一,它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.
(1)应用一:最短路径问题
如图,一只蚂蚁从点沿圆柱侧面爬到相对一侧中点处,如果圆柱的高为,圆柱的底面半径为,那么最短的路线长是______;
(2)应用二:解决实际问题.
如图,某公园有一秋千,秋千静止时,踏板离地的垂直高度,将它往前推至处时,即水平距离,踏板离地的垂直高度,它的绳索始终拉直,求绳索的长.
19.已知,在中,,在外取一点P,连接、,使得,,连接,过点A作于点H.
(1)如图1,若,求的度数;
(2)如图2,若点P在边左侧,请写出线段、、三者之间的数量关系,并说明理由;
(3)如图3,若点P在边右侧,,,求的面积.
20.【问题情境】某消防队在一次应急演练中,消防员架起一架长的云梯,如图,云梯斜靠在一面墙上,这时云梯底端距墙脚的距离.
(1)【独立思考】这架云梯顶端距地面的距离有多高?
(2)【深入探究】消防员接到命令,按要求将云梯从顶端下滑到位置上(云梯长度不改变),,那么梯子的底端外移的距离是多少米?
(3)【问题解决】在演练中,高的墙头有求救声,消防员需调整云梯去救援被困人员.经验表明,云梯靠墙摆放时,如果云梯底端离墙的距离不小于云梯长度的,则云梯和消防员相对安全.在相对安全的前提下,云梯的顶端能否到达高的墙头去救援被困人员?
《第17章勾股定理检测卷-2024-2025学年数学八年级下册人教版》参考答案
题号 1 2 3 4 5 6 7 8
答案 A D B A B A D A
1.A
【分析】本题考查了勾股定理的逆定理以及三角形的三边关系,熟知如果三角形的三边长a,b,c满足,那么这个三角形就是直角三角形是解题的关键.根据勾股定理的逆定理好三角形的三边关系对各选项进行逐一判断即可.
【详解】解:A、,能构成直角三角形,符合题意;
B、,不能构成三角形,更不可能是直角三角形,不符合题意;
C、,不能构成直角三角形,不符合题意;
D、,不能构成直角三角形,不符合题意;
故选:A.
2.D
【分析】本题以网格背景考查勾股定理、三角形面积计算公式.求出的面积、边的长,再利用三角形面积公式列方程求解即可.熟练利用面积法是解题的关键.
【详解】解:设点到线段的距离等于,
∵小正方形的边长为
∴,
,
∵,即,
∴,
∴点到线段的距离为.
故选:D.
3.B
【分析】求出、,根据勾股定理求出,即可得出,求出长即可.
本题考查了勾股定理和坐标与图形性质的应用,解此题的关键是求出的长,注意:在直角三角形中,两直角边的平方和等于斜边的平方.
【详解】解:∵点,点,
∴, ,
在中,由勾股定理得:,
∴,
∴,
∴点C的坐标为,
故选:B.
4.A
【分析】本题考查的是垂线段最短,等腰三角形的性质,勾股定理的应用,掌握“点到直线的距离,垂线段最短”是解题的关键. 在边上移动,由点到直线的距离,垂线段最短,可得当时,最短,再利用勾股定理求解即可.
【详解】解:如图,在边上移动,当时,最短,
,
,
,
所以的最小值是6,
故选:A
5.B
【分析】本题考查勾股定理,应用勾股定理和正方形的面积公式,即可求解.
【详解】解:如图,
正方形③的面积,正方形④的面积,正方形①的面积,
由勾股定理得到:,
∴正方形③和④的面积的和等于最大正方形①的面积,
故A不符合题意;
由勾股定理和正方形的面积公式得到⑦⑨的面积的和等于③的面积,⑧⑩的面积大的和等于④的面积的和,
∴④⑦⑨的面积的和等于最大正方形①的面积,③⑧⑩的面积的和等于最大正方形①的面积,
故C、D不符合题意;
由已知条件不能证明②⑤⑥的面积的和等于最大正方形①的面积,
故B符合题意.
故选:B.
6.A
【分析】本题考查了勾股定理和三角形的面积,勾股定理的逆定理,连接,运用勾股定理逆定理可证为直角三角形,可求出两直角三角形的面积,此块地的面积为两个直角三角形的面积和.
【详解】解:如图,连接,
在中,,,,
由勾股定理得:,
∴(负值已舍去),
在中,,
∴,
∴,
∴.
故答案为:A.
7.D
【分析】此题考查了垂直平分线的性质、直角三角形的性质、勾股定理等知识,熟练掌握这些性质和运用点到直线的距离垂线段最短是解决此题的关键.延长至,使,连接,过点作于,先证明,然后得,当与共线时,为最小值,再根据勾股定理求即可.
【详解】解:如图,延长至,使,连接,过点作于,
∵中,,,,
∴,则,
垂直平分线段,
,
,
,
,
由垂线段最短可知:当与共线时,为最小值,
此时,,
,
,
,
∴的最小值为;
故选:D.
8.A
【分析】本题考查的是勾股定理的应用,善于观察题目的信息,灵活运用勾股定理是解题的关键.
根据勾股定理求出的长,再求出下滑后的,利用勾股定理求出下滑后的,继而求出滑块B滑动的距离.
【详解】解:依题意得:,
设滑动后点A、B的对应位置是,
由勾股定理得,(厘米),
当滑块A向下滑13厘米时,(厘米),
∴(厘米),
∴滑块B滑动的距离为:(厘米),
故选:A.
9.
【分析】本题主要考查了勾股定理,熟练掌握勾股定理的应用是解题的关键.
利用勾股定理即可解答此题.
【详解】解:在中, ,,根据勾股定理得:
.
故答案为:.
10.
【分析】本题考查了三角形内角和性质,勾股定理,30度所对的直角边是斜边的一半,正确掌握相关性质内容是解题的关键.先求出,再根据30度所对的直角边是斜边的一半,得,最后根据勾股定理列式计算,即可作答.
【详解】解:∵
∴,
则,
∴,
故答案为:.
11./
【分析】本题考查了勾股定理,实数与数轴,熟练掌握勾股定理是解题的关键.由题意可知,,再由勾股定理求出,则,然后求出,即可得出结论.
【详解】解:点和分别对应的实数是1和2,
,,
由题意可知,,,
,
,
,
,
,
即点对应的实数是,
故答案为:.
12.100
【分析】本题考查平面展开 最短路径问题,关键知道两点之间线段最短,从而可找到路径求出解.作出A关于的对称点,连接,与交于点Q,此时最短;为直角的斜边,根据勾股定理求解即可.
【详解】解:如图所示作出A关于的对称点,连接,与交于点Q,蚂蚁沿着的路线爬行时路程最短.
则,
根据题意:,,
∴,
∴,
∴最短路线长为,
故答案为:.
13. 200
【分析】本题主要考查等腰三角形的性质,等边三角形的判定与性质,含角的直角三角形的性质以及勾股定理,熟练掌握性质定理是解题的关键.当时,有最小值,此时是等边三角形,即可得到答案,当时,有最大值,根据勾股定理进行求解即可.
【详解】解:由题意可得:当时,有最小值,
是等边三角形,
,最小值为;
当时,有最大值,
过点作于点,
.
故答案为:,.
14.
【分析】本题主要考查了勾股定理,三角形面积计算,勾股定理,过C作于H,连接,根据的面积的面积的面积,得出,证明,求出,即可得出答案.
【详解】解:过C作于H,连接,
∵,,
∴的面积
的面积,
的面积,
∵的面积的面积的面积,
∴,
∵是等边三角形,
∴,,
∴
∴,
∵,
∴,
∴.
故答案为:.
15.为直角三角形,其面积为
【分析】本题考查了勾股定理逆定理,绝对值和算术平方根的非负性,二次根式的运算,求出是解题的关键.
先根据非负性求出,然后根据勾股定理逆定理证明为直角三角形,即可求解面积.
【详解】解:∵,,
∴,
解得:,
∵,
∴,为直角三角形,
∴面积为:.
16.(1)
(2)是直角三角形
(3)
【分析】本题考查了勾股定理及逆定理,熟练掌握勾股定理是解题的关键.
(1)利用勾股定理分别求出的长,即可得到答案;
(2)根据勾股定理的逆定理判断即可;
(3)根据三角形面积公式得到,计算即可得到答案.
【详解】(1)解: ,
,
;
(2)证明:,,,
,
是直角三角形;
(3)解:,
,
.
17.(1)见解析
(2)
【分析】此题综合运用了等腰直角三角形的性质、全等三角形的性质和判定、勾股定理以及分母有理化.解决本题的关键是熟练掌握等腰直角三角形的性质、全等三角形的性质和判定、以及勾股定理.
(1)根据等腰直角三角形的性质证明,再证明,再证明,最后由勾股定理证明即可;
(2)过点C作,由全等三角形的性质可得再证明,设,可得 ,再列出方程求解即可.
【详解】(1)证明:,
,,
又,,
,
.
,
,
;
(2)解:如图,过点C作,
,
,
是等腰直角三角形,
,
设,
是等腰直角三角形,,
,
,
,
,
,
.
18.(1)
(2)绳索的长为
【分析】本题主要考查勾股定理的运用,掌握最短路的计算,勾股定理的计算方法是关键.
(1)根据题意可得圆柱底面圆的周长为,由展开图可得即为最短路径,由勾股定理即可求解;
(2)根据题意得到四边形是矩形,如图所示,过点作,四边形,是矩形,则,,设,则,在中由勾股定理得到,代入计算即可求解.
【详解】(1)解:圆柱的底面半径为,
∴圆柱底面圆的周长为,
如图所示,即为最短路径,,,
∴,
∴最短的路线长是,
故答案为:;
(2)解:根据题意,,
∴四边形是矩形,
∴,
如图所示,过点作,
∴,
∴四边形,是矩形,
∴,
∴,
设,则,
在中,,即,
解得,,
∴绳索的长为.
19.(1)
(2),理由见解析
(3)
【分析】(1)设,则,得到,结合等腰三角形性质得到,,再利用三角形内角和定理建立方程求解,即可解题;
(2)在上取,记与交于点,结合等腰三角形性质证明,作于点,利用全等三角形性质,以及三角形外角性质进而证明,再结合全等三角形性质求解,即可解题.
(3)在上取,由(2)同理可证,,利用全等三角形性质,以及等腰三角形性质得到,结合勾股定理逆定理推出,再利用等腰直角三角形性质得到为与的交点,作,延长交于点,进而证明,结合全等三角形性质得到,进而得到,最后利用三角形面积公式求解,即可解题.
【详解】(1)解:,
设,则,
,
,
,
,
,
,
,
解得,
的度数为;
(2)解:,理由如下:
在上取,记与交于点,
,,
,
,,
,
,,
作于点,
,,
,
于点H,
,
,
,
,,
,
;
(3)解:在上取,
由(2)同理可证,,
,,
于点H, ,
,
,,
,
,
,
,
,
,
,
为与的交点,
,
,
作,延长交于点,
,,
,
,
,
,
,
,
,
.
【点睛】本题考查了等腰三角形性质和判定,三角形内角和定理,全等三角形性质和判定,三角形外角性质,平行线性质,勾股定理逆定理,解题的关键在于作辅助线构造全等三角形.
20.(1)
(2)
(3)能,理由见详解
【分析】本题主要考查勾股定理的运用,熟练掌握勾股定理是解答本题的关键.
(1)根据勾股定理即可求解;
(2)根据题意,运用勾股定理可得,根据即可求解;
(3)根据题意可得相对安全的距离为不小于,运用勾股定理可得云梯能达到的高度,进行比较即可求解.
【详解】(1)解:根据题意,,
∴这架云梯顶端距地面的距离的高为;
(2)解:,,
∴,
∴;
(3)解:能,理由如下,
云梯底端离墙的距离不小于云梯长度的,则云梯和消防员相对安全,
∴相对安全的距离为不小于,
∵云梯的长为,
∴,
∴云梯的顶端能到达高的墙头去救援被困人员.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第17章勾股定理检测卷-2024-2025学年数学八年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.以下列各数为边长,能构成直角三角形的是( )
A.1,1, B.1, 4, C.3,4,6 D.1,3,3
2.如图,在边长为的小正方形网格中,位置如图所示,则点到线段的距离为( )
A. B. C. D.
3.如图,在平面直角坐标系中,点,点,以点A为圆心,以的长为半径画弧,交x正半轴于点C,则点C的坐标为( )
A. B. C. D.
4.如图,在中,有一点P在BC边上移动,若,则AP的最小值为( )
A.6 B.8 C.10 D.12
5.如图所示的所有四边形都是正方形,所有三角形都是直角三角形,在图中找出若干个图形,使得它们的面积之和恰好等于最大正方形①的面积,下列给出的方案中不正确的是( )
A.③④ B.②⑤⑥ C.④⑦⑨ D.③⑧⑩
6.如图,李伯伯家有一块四边形田地,其中,,,,,则这块地的面积为( )
A. B. C. D.
7.如图,在中,是边上一动点,则的最小值是( )
A.6 B. C. D.3
8.如图,两个滑块A,B由一个连杆连接,分别可以在垂直和水平的滑道上滑动.开始时,滑块A距O点20厘米,滑块B距O点15厘米,则当滑块A向下滑13厘米时,滑块B向右滑动了( )
A.9厘米 B.24厘米 C.12厘米 D.15厘米
二、填空题
9.在中, . 若, 则 .
10.如图,在中,,则 .
11.如图,点为数轴的原点,点和分别对应的实数是1和2.过点作射线,以点为圆心,长为半径画弧,交于点;以点为圆心,长为半径画弧,交数轴的正半轴于点,则点对应的实数是 .
12.如图所示的长方体透明玻璃鱼缸,假设其长,高,水深.在水面上紧贴内壁的处有一块面包屑,且.一只蚂蚁想从鱼缸外的点沿鱼缸壁爬进鱼缸内的处吃面包屑,则蚂蚁爬行的最短路线的长为 .
13.《农政全书》记载了中国古代的一种采桑工具——桑梯(如图1),其示意图如图2,已知,与的张角记为,为保证采桑人的安全,可调整的范围是,为固定张角大小的锁链.则锁链长度的最大值为 cm,最小值为 cm.
14.如图,是等边三角形,,点P是延长线上的一点,其中,,则 .
三、解答题
15.已知三角形的三边满足.试判定三角形的形状,并求其面积.
16.如图,正方形网格中的,若小方格边长为1.
(1)求的三边长.
(2)判断是否为直角三角形.
(3)求最长边上的高.
17.如图,和都是等腰直角三角形,,,顶点在的斜边上.
(1)证明:;
(2)若,,则四边形的面积为______.
18.勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题重要的工具之一,也是数形结合的纽带之一,它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.
(1)应用一:最短路径问题
如图,一只蚂蚁从点沿圆柱侧面爬到相对一侧中点处,如果圆柱的高为,圆柱的底面半径为,那么最短的路线长是______;
(2)应用二:解决实际问题.
如图,某公园有一秋千,秋千静止时,踏板离地的垂直高度,将它往前推至处时,即水平距离,踏板离地的垂直高度,它的绳索始终拉直,求绳索的长.
19.已知,在中,,在外取一点P,连接、,使得,,连接,过点A作于点H.
(1)如图1,若,求的度数;
(2)如图2,若点P在边左侧,请写出线段、、三者之间的数量关系,并说明理由;
(3)如图3,若点P在边右侧,,,求的面积.
20.【问题情境】某消防队在一次应急演练中,消防员架起一架长的云梯,如图,云梯斜靠在一面墙上,这时云梯底端距墙脚的距离.
(1)【独立思考】这架云梯顶端距地面的距离有多高?
(2)【深入探究】消防员接到命令,按要求将云梯从顶端下滑到位置上(云梯长度不改变),,那么梯子的底端外移的距离是多少米?
(3)【问题解决】在演练中,高的墙头有求救声,消防员需调整云梯去救援被困人员.经验表明,云梯靠墙摆放时,如果云梯底端离墙的距离不小于云梯长度的,则云梯和消防员相对安全.在相对安全的前提下,云梯的顶端能否到达高的墙头去救援被困人员?
《第17章勾股定理检测卷-2024-2025学年数学八年级下册人教版》参考答案
题号 1 2 3 4 5 6 7 8
答案 A D B A B A D A
1.A
【分析】本题考查了勾股定理的逆定理以及三角形的三边关系,熟知如果三角形的三边长a,b,c满足,那么这个三角形就是直角三角形是解题的关键.根据勾股定理的逆定理好三角形的三边关系对各选项进行逐一判断即可.
【详解】解:A、,能构成直角三角形,符合题意;
B、,不能构成三角形,更不可能是直角三角形,不符合题意;
C、,不能构成直角三角形,不符合题意;
D、,不能构成直角三角形,不符合题意;
故选:A.
2.D
【分析】本题以网格背景考查勾股定理、三角形面积计算公式.求出的面积、边的长,再利用三角形面积公式列方程求解即可.熟练利用面积法是解题的关键.
【详解】解:设点到线段的距离等于,
∵小正方形的边长为
∴,
,
∵,即,
∴,
∴点到线段的距离为.
故选:D.
3.B
【分析】求出、,根据勾股定理求出,即可得出,求出长即可.
本题考查了勾股定理和坐标与图形性质的应用,解此题的关键是求出的长,注意:在直角三角形中,两直角边的平方和等于斜边的平方.
【详解】解:∵点,点,
∴, ,
在中,由勾股定理得:,
∴,
∴,
∴点C的坐标为,
故选:B.
4.A
【分析】本题考查的是垂线段最短,等腰三角形的性质,勾股定理的应用,掌握“点到直线的距离,垂线段最短”是解题的关键. 在边上移动,由点到直线的距离,垂线段最短,可得当时,最短,再利用勾股定理求解即可.
【详解】解:如图,在边上移动,当时,最短,
,
,
,
所以的最小值是6,
故选:A
5.B
【分析】本题考查勾股定理,应用勾股定理和正方形的面积公式,即可求解.
【详解】解:如图,
正方形③的面积,正方形④的面积,正方形①的面积,
由勾股定理得到:,
∴正方形③和④的面积的和等于最大正方形①的面积,
故A不符合题意;
由勾股定理和正方形的面积公式得到⑦⑨的面积的和等于③的面积,⑧⑩的面积大的和等于④的面积的和,
∴④⑦⑨的面积的和等于最大正方形①的面积,③⑧⑩的面积的和等于最大正方形①的面积,
故C、D不符合题意;
由已知条件不能证明②⑤⑥的面积的和等于最大正方形①的面积,
故B符合题意.
故选:B.
6.A
【分析】本题考查了勾股定理和三角形的面积,勾股定理的逆定理,连接,运用勾股定理逆定理可证为直角三角形,可求出两直角三角形的面积,此块地的面积为两个直角三角形的面积和.
【详解】解:如图,连接,
在中,,,,
由勾股定理得:,
∴(负值已舍去),
在中,,
∴,
∴,
∴.
故答案为:A.
7.D
【分析】此题考查了垂直平分线的性质、直角三角形的性质、勾股定理等知识,熟练掌握这些性质和运用点到直线的距离垂线段最短是解决此题的关键.延长至,使,连接,过点作于,先证明,然后得,当与共线时,为最小值,再根据勾股定理求即可.
【详解】解:如图,延长至,使,连接,过点作于,
∵中,,,,
∴,则,
垂直平分线段,
,
,
,
,
由垂线段最短可知:当与共线时,为最小值,
此时,,
,
,
,
∴的最小值为;
故选:D.
8.A
【分析】本题考查的是勾股定理的应用,善于观察题目的信息,灵活运用勾股定理是解题的关键.
根据勾股定理求出的长,再求出下滑后的,利用勾股定理求出下滑后的,继而求出滑块B滑动的距离.
【详解】解:依题意得:,
设滑动后点A、B的对应位置是,
由勾股定理得,(厘米),
当滑块A向下滑13厘米时,(厘米),
∴(厘米),
∴滑块B滑动的距离为:(厘米),
故选:A.
9.
【分析】本题主要考查了勾股定理,熟练掌握勾股定理的应用是解题的关键.
利用勾股定理即可解答此题.
【详解】解:在中, ,,根据勾股定理得:
.
故答案为:.
10.
【分析】本题考查了三角形内角和性质,勾股定理,30度所对的直角边是斜边的一半,正确掌握相关性质内容是解题的关键.先求出,再根据30度所对的直角边是斜边的一半,得,最后根据勾股定理列式计算,即可作答.
【详解】解:∵
∴,
则,
∴,
故答案为:.
11./
【分析】本题考查了勾股定理,实数与数轴,熟练掌握勾股定理是解题的关键.由题意可知,,再由勾股定理求出,则,然后求出,即可得出结论.
【详解】解:点和分别对应的实数是1和2,
,,
由题意可知,,,
,
,
,
,
,
即点对应的实数是,
故答案为:.
12.100
【分析】本题考查平面展开 最短路径问题,关键知道两点之间线段最短,从而可找到路径求出解.作出A关于的对称点,连接,与交于点Q,此时最短;为直角的斜边,根据勾股定理求解即可.
【详解】解:如图所示作出A关于的对称点,连接,与交于点Q,蚂蚁沿着的路线爬行时路程最短.
则,
根据题意:,,
∴,
∴,
∴最短路线长为,
故答案为:.
13. 200
【分析】本题主要考查等腰三角形的性质,等边三角形的判定与性质,含角的直角三角形的性质以及勾股定理,熟练掌握性质定理是解题的关键.当时,有最小值,此时是等边三角形,即可得到答案,当时,有最大值,根据勾股定理进行求解即可.
【详解】解:由题意可得:当时,有最小值,
是等边三角形,
,最小值为;
当时,有最大值,
过点作于点,
.
故答案为:,.
14.
【分析】本题主要考查了勾股定理,三角形面积计算,勾股定理,过C作于H,连接,根据的面积的面积的面积,得出,证明,求出,即可得出答案.
【详解】解:过C作于H,连接,
∵,,
∴的面积
的面积,
的面积,
∵的面积的面积的面积,
∴,
∵是等边三角形,
∴,,
∴
∴,
∵,
∴,
∴.
故答案为:.
15.为直角三角形,其面积为
【分析】本题考查了勾股定理逆定理,绝对值和算术平方根的非负性,二次根式的运算,求出是解题的关键.
先根据非负性求出,然后根据勾股定理逆定理证明为直角三角形,即可求解面积.
【详解】解:∵,,
∴,
解得:,
∵,
∴,为直角三角形,
∴面积为:.
16.(1)
(2)是直角三角形
(3)
【分析】本题考查了勾股定理及逆定理,熟练掌握勾股定理是解题的关键.
(1)利用勾股定理分别求出的长,即可得到答案;
(2)根据勾股定理的逆定理判断即可;
(3)根据三角形面积公式得到,计算即可得到答案.
【详解】(1)解: ,
,
;
(2)证明:,,,
,
是直角三角形;
(3)解:,
,
.
17.(1)见解析
(2)
【分析】此题综合运用了等腰直角三角形的性质、全等三角形的性质和判定、勾股定理以及分母有理化.解决本题的关键是熟练掌握等腰直角三角形的性质、全等三角形的性质和判定、以及勾股定理.
(1)根据等腰直角三角形的性质证明,再证明,再证明,最后由勾股定理证明即可;
(2)过点C作,由全等三角形的性质可得再证明,设,可得 ,再列出方程求解即可.
【详解】(1)证明:,
,,
又,,
,
.
,
,
;
(2)解:如图,过点C作,
,
,
是等腰直角三角形,
,
设,
是等腰直角三角形,,
,
,
,
,
,
.
18.(1)
(2)绳索的长为
【分析】本题主要考查勾股定理的运用,掌握最短路的计算,勾股定理的计算方法是关键.
(1)根据题意可得圆柱底面圆的周长为,由展开图可得即为最短路径,由勾股定理即可求解;
(2)根据题意得到四边形是矩形,如图所示,过点作,四边形,是矩形,则,,设,则,在中由勾股定理得到,代入计算即可求解.
【详解】(1)解:圆柱的底面半径为,
∴圆柱底面圆的周长为,
如图所示,即为最短路径,,,
∴,
∴最短的路线长是,
故答案为:;
(2)解:根据题意,,
∴四边形是矩形,
∴,
如图所示,过点作,
∴,
∴四边形,是矩形,
∴,
∴,
设,则,
在中,,即,
解得,,
∴绳索的长为.
19.(1)
(2),理由见解析
(3)
【分析】(1)设,则,得到,结合等腰三角形性质得到,,再利用三角形内角和定理建立方程求解,即可解题;
(2)在上取,记与交于点,结合等腰三角形性质证明,作于点,利用全等三角形性质,以及三角形外角性质进而证明,再结合全等三角形性质求解,即可解题.
(3)在上取,由(2)同理可证,,利用全等三角形性质,以及等腰三角形性质得到,结合勾股定理逆定理推出,再利用等腰直角三角形性质得到为与的交点,作,延长交于点,进而证明,结合全等三角形性质得到,进而得到,最后利用三角形面积公式求解,即可解题.
【详解】(1)解:,
设,则,
,
,
,
,
,
,
,
解得,
的度数为;
(2)解:,理由如下:
在上取,记与交于点,
,,
,
,,
,
,,
作于点,
,,
,
于点H,
,
,
,
,,
,
;
(3)解:在上取,
由(2)同理可证,,
,,
于点H, ,
,
,,
,
,
,
,
,
,
,
为与的交点,
,
,
作,延长交于点,
,,
,
,
,
,
,
,
,
.
【点睛】本题考查了等腰三角形性质和判定,三角形内角和定理,全等三角形性质和判定,三角形外角性质,平行线性质,勾股定理逆定理,解题的关键在于作辅助线构造全等三角形.
20.(1)
(2)
(3)能,理由见详解
【分析】本题主要考查勾股定理的运用,熟练掌握勾股定理是解答本题的关键.
(1)根据勾股定理即可求解;
(2)根据题意,运用勾股定理可得,根据即可求解;
(3)根据题意可得相对安全的距离为不小于,运用勾股定理可得云梯能达到的高度,进行比较即可求解.
【详解】(1)解:根据题意,,
∴这架云梯顶端距地面的距离的高为;
(2)解:,,
∴,
∴;
(3)解:能,理由如下,
云梯底端离墙的距离不小于云梯长度的,则云梯和消防员相对安全,
∴相对安全的距离为不小于,
∵云梯的长为,
∴,
∴云梯的顶端能到达高的墙头去救援被困人员.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
