1.2动量定理课件--人教版物理选择性必修一
文档属性
| 名称 | 1.2动量定理课件--人教版物理选择性必修一 |

|
|
| 格式 | pptx | ||
| 文件大小 | 36.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-04-03 15:46:45 | ||
图片预览








文档简介
1.2 动量定理
第一章 动量守恒定律
目录
01
课堂引入
02
冲量
03
动量定理
04
动量定理解释生活现象
05
06
课堂总结
流体模型
学习目标
1.知道动量的概念及矢量性
2.掌握动量定理的内容并会应用
3.应用动量定理解释生活中的现象
4.应用动量定理分析流体模型
课堂引入
思考:通过观察视频中猫咪安全着陆的例子,大家能得到什么启示?生活中还有哪些类似的例子?
码头岸边的废旧轮胎
船靠岸时边缘上的废旧轮胎
物体碰撞会受到力的作用,物体动量变化和力有什么关系?
情景探究:在光滑水平面上的质量为m 的物体在水平恒力F 的作用下,经过时间t,速度由v 变为v′.
v
m
O
x
F
F
可得 Ft = mv′ - mv ,即 Ft = p′ - p
①
②
1.定义:
2.物理意义:
3.表达式:
4.单位:
5.方向:
6.强调:
反映了力的作用对时间的累积效应
????=????????
?
矢量 方向与力F 的方向相同
?????????
?
一、冲量
力与力的作用时间的乘积叫作该力的冲量
有力有作用时间就有冲量,与物体是否运动无关
(适用于求恒力的冲量)
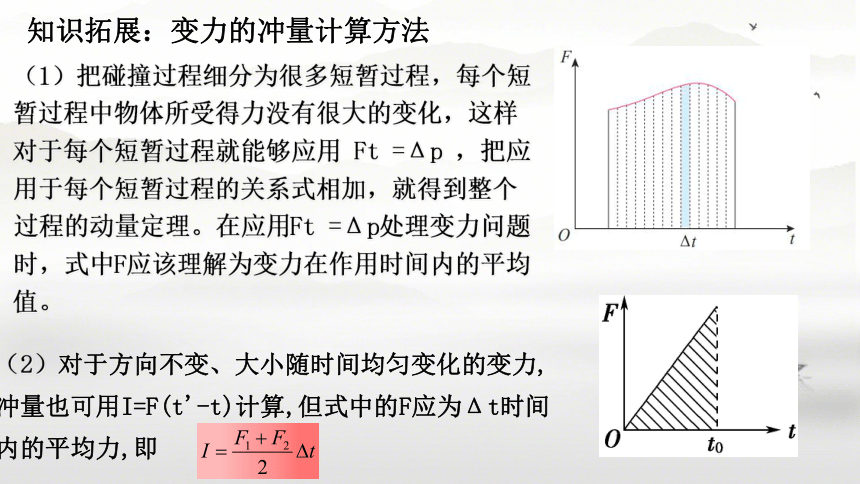
(1)把碰撞过程细分为很多短暂过程,每个短暂过程中物体所受得力没有很大的变化,这样对于每个短暂过程就能够应用 Ft =Δp ,把应用于每个短暂过程的关系式相加,就得到整个过程的动量定理。在应用Ft =Δp处理变力问题时,式中F应该理解为变力在作用时间内的平均值。
知识拓展:变力的冲量计算方法
(2)对于方向不变、大小随时间均匀变化的变力,冲量也可用I=F(t'-t)计算,但式中的F应为Δt时间内的平均力,即
例1:关于冲量的概念,以下说法正确的是( ) A.作用在两个物体上的合力大小不同,但两个物体所受的冲量大小可能相同 B.作用在物体上的力的作用时间很短,物体所受的冲量一定很小 C.作用在物体上的力很大,物体所受的冲量一定也很大 D.只要力的作用时间和力的大小的乘积相同,物体所受的冲量一定相同
答案:C
二、动量定理
1.内容:
2.表达式:
3.理解:
?????????=????????′?????????
?
物体所受合外力的冲量等于它在这个过程中的动量变化量
?????????=????????
?
(1)动量定理的表达式是矢量式,解题时注意规定正方向。
(2)由动量定理推导出????=????????????,动量的变化率等于物体所受的合力。即动量变化快慢。
?
4.动量定理的适用范围
(1)动量定理不但适用于恒力,也适用于随时间变化的变力,对于变力,动量定理中的F应理解为变力在作用时间内的平均值;
(2)动量定理不仅可以解决匀变速直线运动的问题,还可以解决曲线运动中的有关问题,将较难的计算问题转化为较易的计算问题;
(3)动量定理也适用于微观现象和变速运动等问题。
动量定理的优点:不考虑中间过程,只考虑初末状态。
例2.一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒击打后,反向水平飞回,速度大小为45m/s。若球棒与垒球的作用时间为0.002s,求球棒对垒球的平均作用力?
以垒球为研究对象,飞向球棒速度方向为正方向
末动量为
????????=????????????=?-?????.????????????·????/????
?
由动量定理得
平均作用力大小为6300N,方向与垒球飞来的方向相反
????????=????????????=????.????????????·????/????
?
初动量为
????????=????????2?????????1
?
解得:????=?????????????????????
?
明确研究对象和正方向
确定运动过程,找准初末状态
受力分析,列动量定理方程
归纳总结动量定理应用步骤:
1、确定研究对象:一般为单个物体;
4、选定正方向,确定在物理过程中研究对象的动量的变化;
5、根据动量定理列方程,统一单位后代入数据求解。
2、明确物理过程:受力分析,求出合外力的冲量;
3、明确研究对象的初末状态及相应的动量;
三、动量定理解释生活现象
跳高比赛
跳远比赛
悬挂轮胎的游船准备靠岸
这些场景中的垫子、沙坑、轮胎的缓冲为什么可以保护好人和船不受到太大力的作用?
由Ft=Δp可知:
△p一定,t长则F小
例3.两只玻璃杯从同一高度自由落下,掉落在硬质水泥地面易碎,而掉落在松软地毯上不易碎,(假设作用完后速度均变为0),从这一现象中相比较可得出下面说法正确的有( )
A.玻璃杯与毛毯作用时间比玻璃杯与水泥地作用时间长
B.玻璃杯与水泥地面作用过程中动量变化小
C.地毯对玻璃杯作用力较大
D.与水泥地面作用过程中,杯子的动量变化率较大
反思解释:猫从高空掉下不易受伤
人们常说“滴水穿石”,请你根据下面所提供的信息,估算水对石头的冲击力的大小。一瀑布落差为h=20 m,水流量为Q=0.10 m3/s,水的密度ρ=1.0×103 kg/m3,水在最高点和落至石头上后的速度都认为是零。(落在石头上的水立即流走,在讨论石头对水的作用时可以不考虑水的重力,g取10 m/s2)
四、流体模型
思考与讨论
1.基本方法:用动量定理解决流体问题,一般采用微元法:即取一个很短时间Δt,对Δt内流出液体Δm用动量定理。
2.解题的关键:
(1)确定Δm与Δt、液体的速度、密度等关系。
(2)确定Δm作用前后速度的变化。
(3)Δt趋近零时,Δm很小,所受的重力均不计。
3.特点:
⑴对水枪喷射问题,当空中水柱稳定后,空中水的体积不变,任何时间内从枪口射出的水等于射向墙壁或物体的水。
⑵若水柱不散开,水柱的横截面积与水的速度成反比。
【解析】设水滴下落与石头碰前速度为v,则有
设时间Δt内有质量为Δm的水冲到石头上,石头对水的作用力为F,由动量定理得:-FΔt=0-Δmv 又因Δm=ρQΔt 联立得:F=ρQ=2×103 N 由牛顿第三定律,水对石头的作用力F′=F=2×103 N,方向竖直向下。
例4.宇宙飞船进入一个宇宙尘埃区,每前进lm,就有10个平均质量为2×10-7kg的微尘粒与飞船相撞,并附在飞船上。若尘埃微粒原来的速度不计,要保持飞船的速度10 km/s,飞船喷气产生的推力至少应维持多大?
1.内容:物体所受合外力的冲量等于它在这个过程中的动量变化量
F?t=mv′?mv
?
F?t=Δp
?
3.应用:解释现象、计算应用
二、动量定理
一、冲量
3.表达式:
1.定义:
2.物理意义:
力与力的作用时间的乘积叫作该力的冲量
反映了力的作用对时间的累积效应
I=Ft
?
矢量
单位:N?s
?
课堂小结
2.表达式:
课堂练习
1.(冲量的理解)下面关于冲量的说法正确的是( )
A.物体受到很大的冲力时,其冲量一定很大
B.当力与位移垂直时,该力的冲量为零
C.不管物体做什么运动,在相同时间内重力的冲量相同
D.只要力的大小恒定,其相同时间内的冲量就恒定
答案:C
解析:冲量是力与时间的乘积,是矢量,力大,冲量不一定大,A错误;当力与位移垂直时,该力的冲量不为零,B错误;不管物体做什么运动,在相同时间内重力的冲量相同,C正确;力的大小恒定,其相同时间内冲量方向不一定相同,D错误。
课堂练习
2.(动量定理的理解)(多选)在任何相等时间内,物体动量的变化量总是相等的运动可能是( )
A.匀速圆周运动 B.匀变速直线运动
C.自由落体运动 D.平抛运动
答案:BCD
解析:物体做匀变速直线运动、自由落体运动、平抛运动所受的合外力恒定不变。由动量定理可知,它们在任何相等时间内的动量变化量总相等,而物体做匀速圆周运动合外力是变力,故B、C、D均正确,A错误。
课堂练习
3.(定性分析问题)如图所示,从高处跳到低处时,为了安全,一般都要屈腿,这样做是为了( )
A.减小冲量
B.减小动量的变化量
C.增大与地面的冲击时间,从而减小冲力
D.增大人对地面的压强,起到安全作用
答案:C
解析:人在和地面接触时,人的速度减为零,由动量定理可知(F-mg)t=Δp,而屈腿可以增加人着地的时间,从而减小受到地面的冲击力,故选C。
感谢观看
Thank you
第一章 动量守恒定律
目录
01
课堂引入
02
冲量
03
动量定理
04
动量定理解释生活现象
05
06
课堂总结
流体模型
学习目标
1.知道动量的概念及矢量性
2.掌握动量定理的内容并会应用
3.应用动量定理解释生活中的现象
4.应用动量定理分析流体模型
课堂引入
思考:通过观察视频中猫咪安全着陆的例子,大家能得到什么启示?生活中还有哪些类似的例子?
码头岸边的废旧轮胎
船靠岸时边缘上的废旧轮胎
物体碰撞会受到力的作用,物体动量变化和力有什么关系?
情景探究:在光滑水平面上的质量为m 的物体在水平恒力F 的作用下,经过时间t,速度由v 变为v′.
v
m
O
x
F
F
可得 Ft = mv′ - mv ,即 Ft = p′ - p
①
②
1.定义:
2.物理意义:
3.表达式:
4.单位:
5.方向:
6.强调:
反映了力的作用对时间的累积效应
????=????????
?
矢量 方向与力F 的方向相同
?????????
?
一、冲量
力与力的作用时间的乘积叫作该力的冲量
有力有作用时间就有冲量,与物体是否运动无关
(适用于求恒力的冲量)
(1)把碰撞过程细分为很多短暂过程,每个短暂过程中物体所受得力没有很大的变化,这样对于每个短暂过程就能够应用 Ft =Δp ,把应用于每个短暂过程的关系式相加,就得到整个过程的动量定理。在应用Ft =Δp处理变力问题时,式中F应该理解为变力在作用时间内的平均值。
知识拓展:变力的冲量计算方法
(2)对于方向不变、大小随时间均匀变化的变力,冲量也可用I=F(t'-t)计算,但式中的F应为Δt时间内的平均力,即
例1:关于冲量的概念,以下说法正确的是( ) A.作用在两个物体上的合力大小不同,但两个物体所受的冲量大小可能相同 B.作用在物体上的力的作用时间很短,物体所受的冲量一定很小 C.作用在物体上的力很大,物体所受的冲量一定也很大 D.只要力的作用时间和力的大小的乘积相同,物体所受的冲量一定相同
答案:C
二、动量定理
1.内容:
2.表达式:
3.理解:
?????????=????????′?????????
?
物体所受合外力的冲量等于它在这个过程中的动量变化量
?????????=????????
?
(1)动量定理的表达式是矢量式,解题时注意规定正方向。
(2)由动量定理推导出????=????????????,动量的变化率等于物体所受的合力。即动量变化快慢。
?
4.动量定理的适用范围
(1)动量定理不但适用于恒力,也适用于随时间变化的变力,对于变力,动量定理中的F应理解为变力在作用时间内的平均值;
(2)动量定理不仅可以解决匀变速直线运动的问题,还可以解决曲线运动中的有关问题,将较难的计算问题转化为较易的计算问题;
(3)动量定理也适用于微观现象和变速运动等问题。
动量定理的优点:不考虑中间过程,只考虑初末状态。
例2.一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒击打后,反向水平飞回,速度大小为45m/s。若球棒与垒球的作用时间为0.002s,求球棒对垒球的平均作用力?
以垒球为研究对象,飞向球棒速度方向为正方向
末动量为
????????=????????????=?-?????.????????????·????/????
?
由动量定理得
平均作用力大小为6300N,方向与垒球飞来的方向相反
????????=????????????=????.????????????·????/????
?
初动量为
????????=????????2?????????1
?
解得:????=?????????????????????
?
明确研究对象和正方向
确定运动过程,找准初末状态
受力分析,列动量定理方程
归纳总结动量定理应用步骤:
1、确定研究对象:一般为单个物体;
4、选定正方向,确定在物理过程中研究对象的动量的变化;
5、根据动量定理列方程,统一单位后代入数据求解。
2、明确物理过程:受力分析,求出合外力的冲量;
3、明确研究对象的初末状态及相应的动量;
三、动量定理解释生活现象
跳高比赛
跳远比赛
悬挂轮胎的游船准备靠岸
这些场景中的垫子、沙坑、轮胎的缓冲为什么可以保护好人和船不受到太大力的作用?
由Ft=Δp可知:
△p一定,t长则F小
例3.两只玻璃杯从同一高度自由落下,掉落在硬质水泥地面易碎,而掉落在松软地毯上不易碎,(假设作用完后速度均变为0),从这一现象中相比较可得出下面说法正确的有( )
A.玻璃杯与毛毯作用时间比玻璃杯与水泥地作用时间长
B.玻璃杯与水泥地面作用过程中动量变化小
C.地毯对玻璃杯作用力较大
D.与水泥地面作用过程中,杯子的动量变化率较大
反思解释:猫从高空掉下不易受伤
人们常说“滴水穿石”,请你根据下面所提供的信息,估算水对石头的冲击力的大小。一瀑布落差为h=20 m,水流量为Q=0.10 m3/s,水的密度ρ=1.0×103 kg/m3,水在最高点和落至石头上后的速度都认为是零。(落在石头上的水立即流走,在讨论石头对水的作用时可以不考虑水的重力,g取10 m/s2)
四、流体模型
思考与讨论
1.基本方法:用动量定理解决流体问题,一般采用微元法:即取一个很短时间Δt,对Δt内流出液体Δm用动量定理。
2.解题的关键:
(1)确定Δm与Δt、液体的速度、密度等关系。
(2)确定Δm作用前后速度的变化。
(3)Δt趋近零时,Δm很小,所受的重力均不计。
3.特点:
⑴对水枪喷射问题,当空中水柱稳定后,空中水的体积不变,任何时间内从枪口射出的水等于射向墙壁或物体的水。
⑵若水柱不散开,水柱的横截面积与水的速度成反比。
【解析】设水滴下落与石头碰前速度为v,则有
设时间Δt内有质量为Δm的水冲到石头上,石头对水的作用力为F,由动量定理得:-FΔt=0-Δmv 又因Δm=ρQΔt 联立得:F=ρQ=2×103 N 由牛顿第三定律,水对石头的作用力F′=F=2×103 N,方向竖直向下。
例4.宇宙飞船进入一个宇宙尘埃区,每前进lm,就有10个平均质量为2×10-7kg的微尘粒与飞船相撞,并附在飞船上。若尘埃微粒原来的速度不计,要保持飞船的速度10 km/s,飞船喷气产生的推力至少应维持多大?
1.内容:物体所受合外力的冲量等于它在这个过程中的动量变化量
F?t=mv′?mv
?
F?t=Δp
?
3.应用:解释现象、计算应用
二、动量定理
一、冲量
3.表达式:
1.定义:
2.物理意义:
力与力的作用时间的乘积叫作该力的冲量
反映了力的作用对时间的累积效应
I=Ft
?
矢量
单位:N?s
?
课堂小结
2.表达式:
课堂练习
1.(冲量的理解)下面关于冲量的说法正确的是( )
A.物体受到很大的冲力时,其冲量一定很大
B.当力与位移垂直时,该力的冲量为零
C.不管物体做什么运动,在相同时间内重力的冲量相同
D.只要力的大小恒定,其相同时间内的冲量就恒定
答案:C
解析:冲量是力与时间的乘积,是矢量,力大,冲量不一定大,A错误;当力与位移垂直时,该力的冲量不为零,B错误;不管物体做什么运动,在相同时间内重力的冲量相同,C正确;力的大小恒定,其相同时间内冲量方向不一定相同,D错误。
课堂练习
2.(动量定理的理解)(多选)在任何相等时间内,物体动量的变化量总是相等的运动可能是( )
A.匀速圆周运动 B.匀变速直线运动
C.自由落体运动 D.平抛运动
答案:BCD
解析:物体做匀变速直线运动、自由落体运动、平抛运动所受的合外力恒定不变。由动量定理可知,它们在任何相等时间内的动量变化量总相等,而物体做匀速圆周运动合外力是变力,故B、C、D均正确,A错误。
课堂练习
3.(定性分析问题)如图所示,从高处跳到低处时,为了安全,一般都要屈腿,这样做是为了( )
A.减小冲量
B.减小动量的变化量
C.增大与地面的冲击时间,从而减小冲力
D.增大人对地面的压强,起到安全作用
答案:C
解析:人在和地面接触时,人的速度减为零,由动量定理可知(F-mg)t=Δp,而屈腿可以增加人着地的时间,从而减小受到地面的冲击力,故选C。
感谢观看
Thank you
