6.3 密度知识的应用 导学案 (含答案)2024-2025学年物理苏科版八年级下册
文档属性
| 名称 | 6.3 密度知识的应用 导学案 (含答案)2024-2025学年物理苏科版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 75.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-04-03 17:03:36 | ||
图片预览

文档简介
三、 密度知识的应用
第1课时 测量物质的密度
1. 实验室中常用 或 测量液体的体积,其标度的单位是 。1mL= cm3。
2. 把量筒放在 上,在其中注入一定量的水,读数时视线与水凹面的 相平。
3. 测量物质的密度所依据的原理是 ;所需的测量器材是 和 ;测量的合理步骤通常是先测 ,后测 。
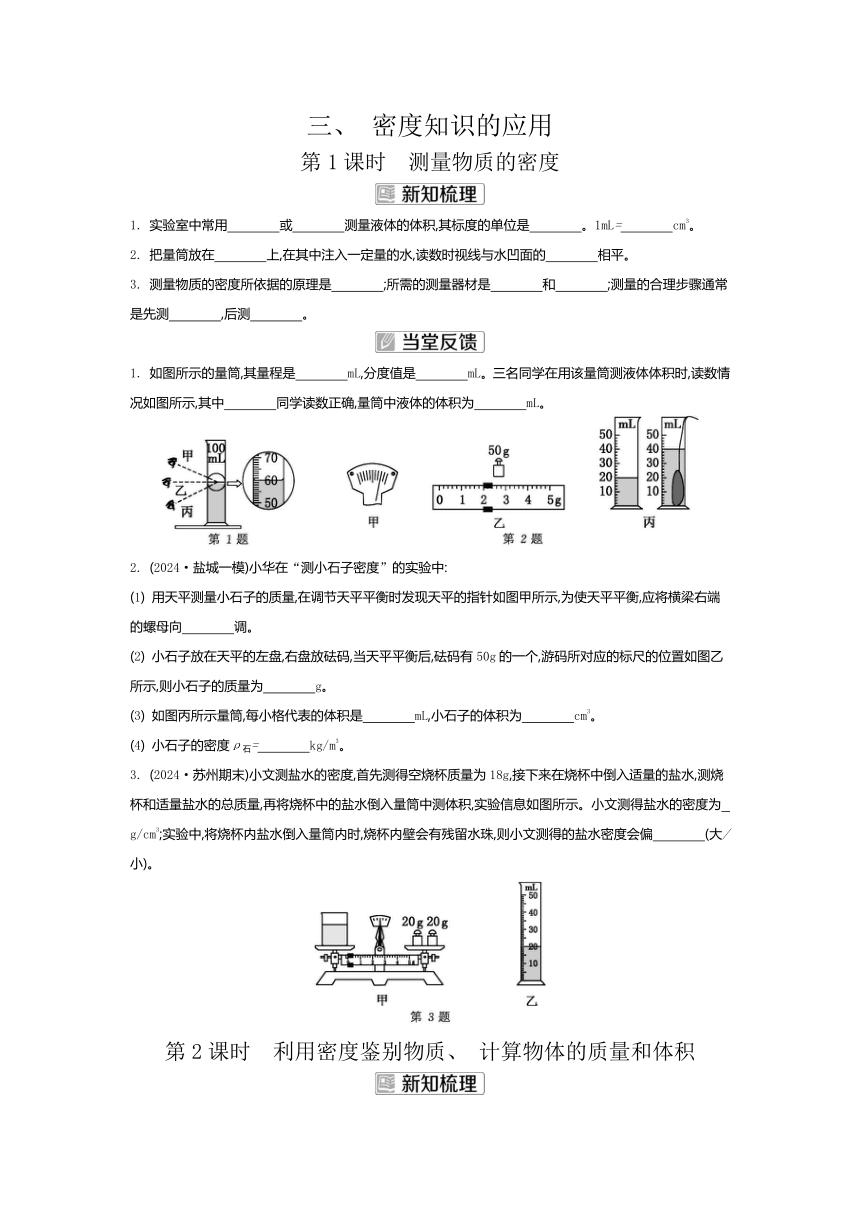
1. 如图所示的量筒,其量程是 mL,分度值是 mL。三名同学在用该量筒测液体体积时,读数情况如图所示,其中 同学读数正确,量筒中液体的体积为 mL。
2. (2024·盐城一模)小华在“测小石子密度”的实验中:
(1) 用天平测量小石子的质量,在调节天平平衡时发现天平的指针如图甲所示,为使天平平衡,应将横梁右端的螺母向 调。
(2) 小石子放在天平的左盘,右盘放砝码,当天平平衡后,砝码有50g的一个,游码所对应的标尺的位置如图乙所示,则小石子的质量为 g。
(3) 如图丙所示量筒,每小格代表的体积是 mL,小石子的体积为 cm3。
(4) 小石子的密度ρ石= kg/m3。
3. (2024·苏州期末)小文测盐水的密度,首先测得空烧杯质量为18g,接下来在烧杯中倒入适量的盐水,测烧杯和适量盐水的总质量,再将烧杯中的盐水倒入量筒中测体积,实验信息如图所示。小文测得盐水的密度为 g/cm3;实验中,将烧杯内盐水倒入量筒内时,烧杯内壁会有残留水珠,则小文测得的盐水密度会偏 (大/小)。
第2课时 利用密度鉴别物质、 计算物体的质量和体积
1. 利用密度知识鉴别物质时,首先通过实验测出样品的 ,再与 对比,从而大致判断出物质的种类。除了可以鉴别物质的种类,用测量密度的方法还可以鉴别某些样品是否 。
2. 利用密度知识间接测量物体的质量或体积。
(1) 若物体的质量较大,在已知组成物体的物质的密度ρ时,通过测量物体的 ,利用公式m= 得到该物体的质量。
(2) 若物体的形状不规则,在已知组成物体的物质的密度ρ时,通过测量物体的 ,利用公式V= 得到该物体的体积。
1. 一个实心铅球的质量是4kg,经测量,它的体积是0.57×10-3 m3,则这个铅球是用纯铅制成的吗 (已知ρ铅=11.3×103 kg/m3)
2. 一块石碑的体积为20m3,为了计算它的质量,测得这块石碑岩石样品的质量为120g,用量筒装入100mL的水,然后将这块样品浸没在水中,此时水面升高到150mL刻度线处。求:
(1) 这块石碑岩石样品的密度。
(2) 这块石碑的质量。
3. 某古式酒壶是由贵金属材料制成的。用天平测出整个酒壶的质量为980g,其中壶盖的质量为89g,把壶盖浸没在装满水的溢水杯中,测得溢出水的质量是10g。已知水的密度为1g/cm3。求:
(1) 这种材料的密度。
(2) 制作整个酒壶所用材料的体积。(结果保留整数)
三、 密度知识的应用
第1课时 测量物质的密度
1. 量筒 量杯 毫升(mL) 1 2. 水平台面 底部 3. ρ= 天平 量筒 质量 体积
1. 0~100 1 乙 60 2. (1) 左 (2) 52 (3) 2 20 (4) 2.6×103 3. 1.1 大
第2课时 利用密度鉴别物质、计算物体的
质量和体积
1. 密度 密度表中的密度值 合格 2. (1) 体积 ρV (2) 质量
1. 此实心铅球的密度ρ球==≈7.0×103kg/m3。因为ρ球<ρ铅,所以此球不是用纯铅制成的 2. (1) 2.4×103kg/m3 (2) 4.8×104kg 3. (1) 已知酒壶的质量m=980g、壶盖的质量 m1=89g、溢出水的质量m2=10g,则壶盖的体积V壶盖=V溢===10cm3。材料的密度即壶盖的密度,ρ材料=ρ壶盖===8.9g/cm3 (2) 制作整个酒壶所用材料的体积V==≈110cm3
第1课时 测量物质的密度
1. 实验室中常用 或 测量液体的体积,其标度的单位是 。1mL= cm3。
2. 把量筒放在 上,在其中注入一定量的水,读数时视线与水凹面的 相平。
3. 测量物质的密度所依据的原理是 ;所需的测量器材是 和 ;测量的合理步骤通常是先测 ,后测 。
1. 如图所示的量筒,其量程是 mL,分度值是 mL。三名同学在用该量筒测液体体积时,读数情况如图所示,其中 同学读数正确,量筒中液体的体积为 mL。
2. (2024·盐城一模)小华在“测小石子密度”的实验中:
(1) 用天平测量小石子的质量,在调节天平平衡时发现天平的指针如图甲所示,为使天平平衡,应将横梁右端的螺母向 调。
(2) 小石子放在天平的左盘,右盘放砝码,当天平平衡后,砝码有50g的一个,游码所对应的标尺的位置如图乙所示,则小石子的质量为 g。
(3) 如图丙所示量筒,每小格代表的体积是 mL,小石子的体积为 cm3。
(4) 小石子的密度ρ石= kg/m3。
3. (2024·苏州期末)小文测盐水的密度,首先测得空烧杯质量为18g,接下来在烧杯中倒入适量的盐水,测烧杯和适量盐水的总质量,再将烧杯中的盐水倒入量筒中测体积,实验信息如图所示。小文测得盐水的密度为 g/cm3;实验中,将烧杯内盐水倒入量筒内时,烧杯内壁会有残留水珠,则小文测得的盐水密度会偏 (大/小)。
第2课时 利用密度鉴别物质、 计算物体的质量和体积
1. 利用密度知识鉴别物质时,首先通过实验测出样品的 ,再与 对比,从而大致判断出物质的种类。除了可以鉴别物质的种类,用测量密度的方法还可以鉴别某些样品是否 。
2. 利用密度知识间接测量物体的质量或体积。
(1) 若物体的质量较大,在已知组成物体的物质的密度ρ时,通过测量物体的 ,利用公式m= 得到该物体的质量。
(2) 若物体的形状不规则,在已知组成物体的物质的密度ρ时,通过测量物体的 ,利用公式V= 得到该物体的体积。
1. 一个实心铅球的质量是4kg,经测量,它的体积是0.57×10-3 m3,则这个铅球是用纯铅制成的吗 (已知ρ铅=11.3×103 kg/m3)
2. 一块石碑的体积为20m3,为了计算它的质量,测得这块石碑岩石样品的质量为120g,用量筒装入100mL的水,然后将这块样品浸没在水中,此时水面升高到150mL刻度线处。求:
(1) 这块石碑岩石样品的密度。
(2) 这块石碑的质量。
3. 某古式酒壶是由贵金属材料制成的。用天平测出整个酒壶的质量为980g,其中壶盖的质量为89g,把壶盖浸没在装满水的溢水杯中,测得溢出水的质量是10g。已知水的密度为1g/cm3。求:
(1) 这种材料的密度。
(2) 制作整个酒壶所用材料的体积。(结果保留整数)
三、 密度知识的应用
第1课时 测量物质的密度
1. 量筒 量杯 毫升(mL) 1 2. 水平台面 底部 3. ρ= 天平 量筒 质量 体积
1. 0~100 1 乙 60 2. (1) 左 (2) 52 (3) 2 20 (4) 2.6×103 3. 1.1 大
第2课时 利用密度鉴别物质、计算物体的
质量和体积
1. 密度 密度表中的密度值 合格 2. (1) 体积 ρV (2) 质量
1. 此实心铅球的密度ρ球==≈7.0×103kg/m3。因为ρ球<ρ铅,所以此球不是用纯铅制成的 2. (1) 2.4×103kg/m3 (2) 4.8×104kg 3. (1) 已知酒壶的质量m=980g、壶盖的质量 m1=89g、溢出水的质量m2=10g,则壶盖的体积V壶盖=V溢===10cm3。材料的密度即壶盖的密度,ρ材料=ρ壶盖===8.9g/cm3 (2) 制作整个酒壶所用材料的体积V==≈110cm3
