第12章 二次根式 素能测评(含答案) 2024-2025学年数学苏科版八年级下册
文档属性
| 名称 | 第12章 二次根式 素能测评(含答案) 2024-2025学年数学苏科版八年级下册 | 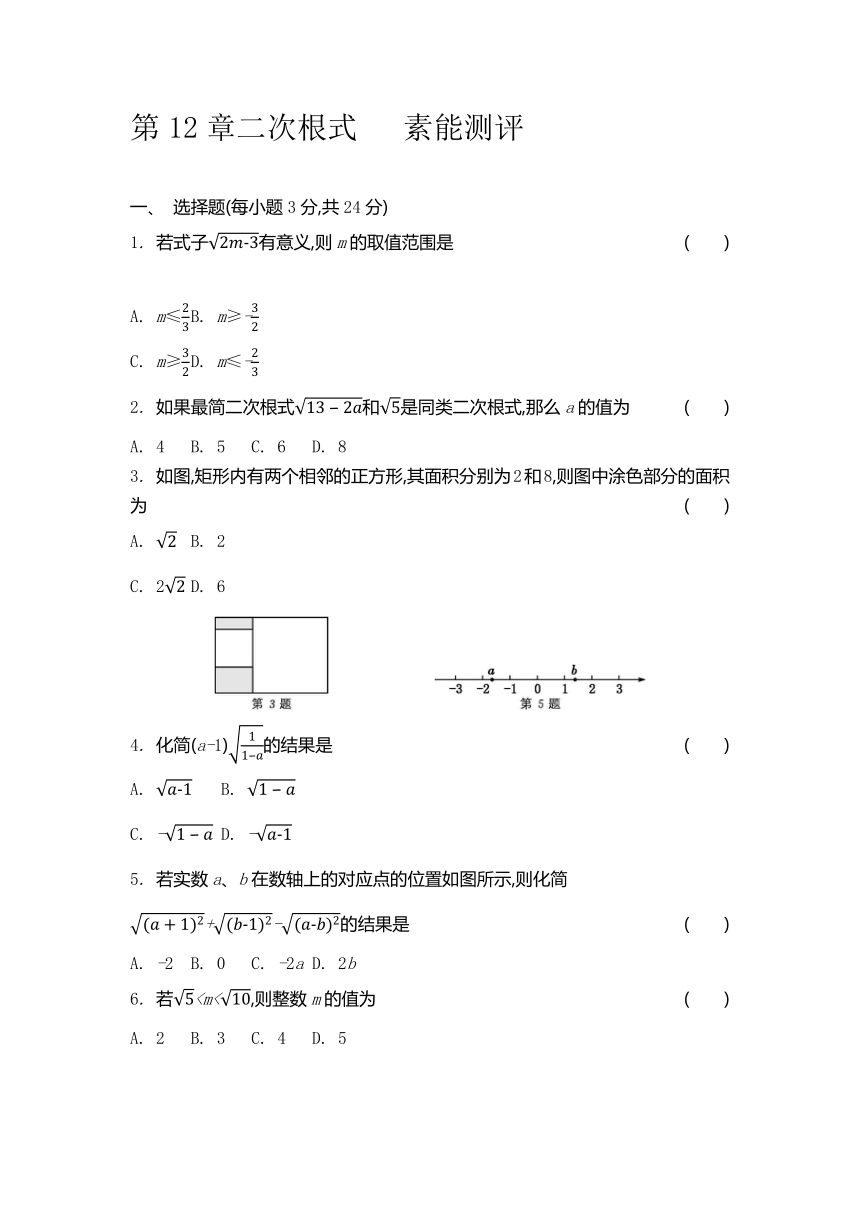 | |
| 格式 | docx | ||
| 文件大小 | 63.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-03 18:14:21 | ||
图片预览



文档简介
第12章二次根式 素能测评
一、 选择题(每小题3分,共24分)
1. 若式子有意义,则m的取值范围是 ( )
A. m≤ B. m≥-
C. m≥ D. m≤-
2. 如果最简二次根式和是同类二次根式,那么a的值为 ( )
A. 4 B. 5 C. 6 D. 8
3. 如图,矩形内有两个相邻的正方形,其面积分别为2和8,则图中涂色部分的面积为 ( )
A. B. 2
C. 2 D. 6
4. 化简(a-1)的结果是 ( )
A. B.
C. - D. -
5. 若实数a、b在数轴上的对应点的位置如图所示,则化简+-的结果是 ( )
A. -2 B. 0 C. -2a D. 2b
6. 若A. 2 B. 3 C. 4 D. 5
7. 如果等腰三角形的两边长分别为2和5,那么这个等腰三角形的周长为 ( )
A. 4+5 B. 10+2
C. 4+5或10+2 D. 10+4
8. 已知a>b>0,且a2+b2=3ab,则÷的值是 ( )
A. B. -
C. D. -
二、 填空题(每小题3分,共24分)
9. 一个二次根式与的乘积是有理数,这个二次根式可以为 (写出一个即可).
10. 比较大小:-6 -5(填“>”“<”或“=”).
11. 在实数范围内分解因式:x2-2x+7= .
12. 在如图所示的方格中,要使横行、竖列、斜对角的3个实数相乘都得到同样的结果,则2个空格中的实数之积为 .
3 2
1 6
3
13. 已知一个等腰直角三角形的面积为16,则这个等腰直角三角形的周长为 .
14. 若的整数部分是a,小数部分是b,则 b-a的值为 .
15. 已知x=-2-1,y=1-2,则x2-y2的值为 .
16. 如图,在等腰直角三角形ABC中,∠ACB=90°,AB=,C是矩形ECGF与△ABC的公共顶点,且CE=1,CG=3,D是CB延长线上一点,且CD=2.连接BG、DF,在矩形ECGF绕点C按顺时针方向旋转一周的过程中,当线段BG达到最长和最短时,线段DF对应的长度分别为m和n,则的值为 .
三、 解答题(共82分)
17. (5分)若最简二次根式与可以合并,求x的值.
18. (5分)计算:
(1) -; (2) -+.
19. (6分)计算:
(1) ÷×2-6; (2) (2-)×(2+)-()2.
20. (6分)化简:
(1) ÷×; (2) ÷(x>0).
21. (6分)先化简,再求值:÷,其中a=+1.
22. (8分)已知实数a、b、c在数轴上的位置如图所示,化简:|a|-+-.
23. (8分)已知y=2+3+,求÷的值.
24. (8分)已知菱形ABCD的两条对角线的长分别为2+2和2-2,求菱形ABCD的周长和面积.
25. (10分)[素材引入] 若一个三角形的三边长分别为a、b、c,记p=(a+b+c),即p为△ABC的周长的一半,则S△ABC=.
(1) 现有一块三角形空地A,它的三边长分别为3m、5m、6m,求这块三角形空地的面积;
(2) 若空地B的面积为m2,则空地A的面积是空地B面积的几倍
26. (10分)已知x=2-,y=2+.
(1) 求x+y和xy的值;
(2) 求x2+y2-3xy的值;
(3) 若x的小数部分是a,y的整数部分是b,求ax-by的值.
27. (10分)请阅读以下材料,并完成相应的任务.
斐波那契是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果.在实际生活中,很多花朵(如梅花、飞燕草、万寿菊)的瓣数恰是斐波那契数列中的数.斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.斐波那契数列中的第n个数可以用表示,其中n≥1.这是用无理数表示有理数的一个范例.
(1) 通过计算求出斐波那契数列中的第1个数和第2个数;
(2) 求证:斐波那契数列中的连续三个数xn-1、xn和xn+1之间存在以下关系:xn+1-xn=xn-1(n为正整数,且n≥2).
第12章素能测评
一、 1. C 2. A 3. B 4. C 5. A 6. B
7. B 解析:当三边长为2、2与5时,由于2+2<5,因此不能构造三角形.当三边长为5、5与2时,可以构造等腰三角形,此时周长为5+5+2=10+2.
8. B 解析:原式=-.∵ a2+b2=3ab,∴ (a+b)2=5ab,(a-b)2=ab.∵ a>b>0,∴ a+b=,a-b=.∴ 原式=-=-=-.
二、 9. 答案不唯一,如 10. < 11. (x-)2 12. 6 13. 8+8 14. 3-2 15. 8
16. 解析:当点G在线段BC的延长线上时,线段BG最长,此时DF的长为;当点G在线段CB的延长线上时,线段BG最短,此时DF的长为.∴ =.
三、 17. ∵ 最简二次根式与可以合并,∴ 与是同类二次根式.∴ 5x+8=13,解得x=1
18. (1) - (2) 4
19. (1) 6 (2) 3
20. (1) (2) -3
21. 原式=.当a=+1时,原式===
22. 由数轴,可知c23. 由题意,得解得x=.∴ y=.∴ 原式=÷=·=2y=
24. ∵ 易知菱形ABCD的边长为=2,∴ 菱形ABCD的周长为2×4=8,面积为×(2+2)×(2-2)=4
25. (1) 由题意,得p=×(3+5+6)=7(m).∴ 这块三角形空地的面积为=2(m2) (2) ∵ 2÷=,∴ 空地A的面积是空地B面积的倍
26. (1) ∵ x=2-,y=2+,∴ x+y=2-+2+=4,xy=(2-)×(2+)=4-3=1 (2) 由(1),得x+y=4,xy=1.∴ x2+y2-3xy=(x+y)2-5xy=42-5×1=11 (3) ∵ 1<3<4,∴ <<,即1<<2.∴ -2<-<-1.∴ 0<2-<1.∵ x的小数部分是a,∴ a=2-.∵ 3<2+<4,y的整数部分是b,∴ b=3.∴ ax-by=(2-)×(2-)-3×(2+)=4-4+3-6-3=1-7
27. (1) 当n=1时,可得第1个数为×-=×=1;当n=2时,可得第2个数为×-=××=×1×=1 (2) xn+1-xn=-- -=×--+=××-×=×××-××=×=xn-1,即xn+1-xn=xn-1
一、 选择题(每小题3分,共24分)
1. 若式子有意义,则m的取值范围是 ( )
A. m≤ B. m≥-
C. m≥ D. m≤-
2. 如果最简二次根式和是同类二次根式,那么a的值为 ( )
A. 4 B. 5 C. 6 D. 8
3. 如图,矩形内有两个相邻的正方形,其面积分别为2和8,则图中涂色部分的面积为 ( )
A. B. 2
C. 2 D. 6
4. 化简(a-1)的结果是 ( )
A. B.
C. - D. -
5. 若实数a、b在数轴上的对应点的位置如图所示,则化简+-的结果是 ( )
A. -2 B. 0 C. -2a D. 2b
6. 若
7. 如果等腰三角形的两边长分别为2和5,那么这个等腰三角形的周长为 ( )
A. 4+5 B. 10+2
C. 4+5或10+2 D. 10+4
8. 已知a>b>0,且a2+b2=3ab,则÷的值是 ( )
A. B. -
C. D. -
二、 填空题(每小题3分,共24分)
9. 一个二次根式与的乘积是有理数,这个二次根式可以为 (写出一个即可).
10. 比较大小:-6 -5(填“>”“<”或“=”).
11. 在实数范围内分解因式:x2-2x+7= .
12. 在如图所示的方格中,要使横行、竖列、斜对角的3个实数相乘都得到同样的结果,则2个空格中的实数之积为 .
3 2
1 6
3
13. 已知一个等腰直角三角形的面积为16,则这个等腰直角三角形的周长为 .
14. 若的整数部分是a,小数部分是b,则 b-a的值为 .
15. 已知x=-2-1,y=1-2,则x2-y2的值为 .
16. 如图,在等腰直角三角形ABC中,∠ACB=90°,AB=,C是矩形ECGF与△ABC的公共顶点,且CE=1,CG=3,D是CB延长线上一点,且CD=2.连接BG、DF,在矩形ECGF绕点C按顺时针方向旋转一周的过程中,当线段BG达到最长和最短时,线段DF对应的长度分别为m和n,则的值为 .
三、 解答题(共82分)
17. (5分)若最简二次根式与可以合并,求x的值.
18. (5分)计算:
(1) -; (2) -+.
19. (6分)计算:
(1) ÷×2-6; (2) (2-)×(2+)-()2.
20. (6分)化简:
(1) ÷×; (2) ÷(x>0).
21. (6分)先化简,再求值:÷,其中a=+1.
22. (8分)已知实数a、b、c在数轴上的位置如图所示,化简:|a|-+-.
23. (8分)已知y=2+3+,求÷的值.
24. (8分)已知菱形ABCD的两条对角线的长分别为2+2和2-2,求菱形ABCD的周长和面积.
25. (10分)[素材引入] 若一个三角形的三边长分别为a、b、c,记p=(a+b+c),即p为△ABC的周长的一半,则S△ABC=.
(1) 现有一块三角形空地A,它的三边长分别为3m、5m、6m,求这块三角形空地的面积;
(2) 若空地B的面积为m2,则空地A的面积是空地B面积的几倍
26. (10分)已知x=2-,y=2+.
(1) 求x+y和xy的值;
(2) 求x2+y2-3xy的值;
(3) 若x的小数部分是a,y的整数部分是b,求ax-by的值.
27. (10分)请阅读以下材料,并完成相应的任务.
斐波那契是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果.在实际生活中,很多花朵(如梅花、飞燕草、万寿菊)的瓣数恰是斐波那契数列中的数.斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.斐波那契数列中的第n个数可以用表示,其中n≥1.这是用无理数表示有理数的一个范例.
(1) 通过计算求出斐波那契数列中的第1个数和第2个数;
(2) 求证:斐波那契数列中的连续三个数xn-1、xn和xn+1之间存在以下关系:xn+1-xn=xn-1(n为正整数,且n≥2).
第12章素能测评
一、 1. C 2. A 3. B 4. C 5. A 6. B
7. B 解析:当三边长为2、2与5时,由于2+2<5,因此不能构造三角形.当三边长为5、5与2时,可以构造等腰三角形,此时周长为5+5+2=10+2.
8. B 解析:原式=-.∵ a2+b2=3ab,∴ (a+b)2=5ab,(a-b)2=ab.∵ a>b>0,∴ a+b=,a-b=.∴ 原式=-=-=-.
二、 9. 答案不唯一,如 10. < 11. (x-)2 12. 6 13. 8+8 14. 3-2 15. 8
16. 解析:当点G在线段BC的延长线上时,线段BG最长,此时DF的长为;当点G在线段CB的延长线上时,线段BG最短,此时DF的长为.∴ =.
三、 17. ∵ 最简二次根式与可以合并,∴ 与是同类二次根式.∴ 5x+8=13,解得x=1
18. (1) - (2) 4
19. (1) 6 (2) 3
20. (1) (2) -3
21. 原式=.当a=+1时,原式===
22. 由数轴,可知c
24. ∵ 易知菱形ABCD的边长为=2,∴ 菱形ABCD的周长为2×4=8,面积为×(2+2)×(2-2)=4
25. (1) 由题意,得p=×(3+5+6)=7(m).∴ 这块三角形空地的面积为=2(m2) (2) ∵ 2÷=,∴ 空地A的面积是空地B面积的倍
26. (1) ∵ x=2-,y=2+,∴ x+y=2-+2+=4,xy=(2-)×(2+)=4-3=1 (2) 由(1),得x+y=4,xy=1.∴ x2+y2-3xy=(x+y)2-5xy=42-5×1=11 (3) ∵ 1<3<4,∴ <<,即1<<2.∴ -2<-<-1.∴ 0<2-<1.∵ x的小数部分是a,∴ a=2-.∵ 3<2+<4,y的整数部分是b,∴ b=3.∴ ax-by=(2-)×(2-)-3×(2+)=4-4+3-6-3=1-7
27. (1) 当n=1时,可得第1个数为×-=×=1;当n=2时,可得第2个数为×-=××=×1×=1 (2) xn+1-xn=-- -=×--+=××-×=×××-××=×=xn-1,即xn+1-xn=xn-1
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
