9.1 图形的旋转 同步练(含答案)2024-2025学年数学苏科版八年级下册
文档属性
| 名称 | 9.1 图形的旋转 同步练(含答案)2024-2025学年数学苏科版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 155.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-03 00:00:00 | ||
图片预览

文档简介
9.1 图形的旋转
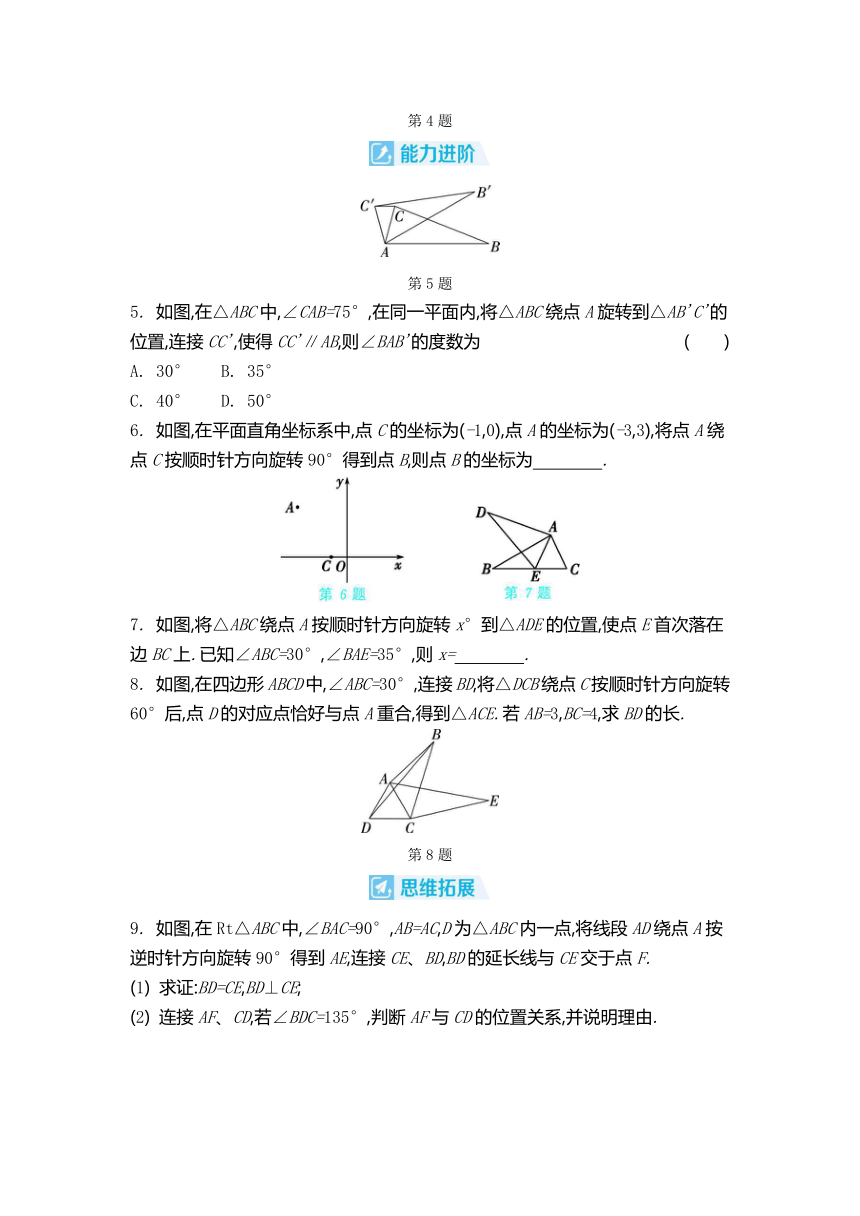
1.
如图,将正方形ABCD中的涂色三角形绕点A按顺时针方向旋转90°后,得到的图形为 ( )
2. 如图,在平面直角坐标系中,点A的坐标为(0,3),点B的坐标为(4,0),连接AB.若将△ABO绕点B按顺时针方向旋转90°,得到△A'BO',则点A'的坐标为 .
3. (2024·滨州)将一副三角尺按如图①所示的方式摆放,把三角尺AOB绕公共顶点O按顺时针方向旋转至如图②所示的位置,此时AB∥OD,则∠1的度数为 .
4. 如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(0,4),B(0,2),C(3,2).
(1) 将△ABC以点O为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2) 将△ABC平移后得到△A2B2C2,若点A的对应点A2的坐标为(2,2),求△A1C1C2的面积.
第4题
第5题
5. 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB'C'的位置,连接CC',使得CC'∥AB,则∠BAB'的度数为 ( )
A. 30° B. 35°
C. 40° D. 50°
6. 如图,在平面直角坐标系中,点C的坐标为(-1,0),点A的坐标为(-3,3),将点A绕点C按顺时针方向旋转90°得到点B,则点B的坐标为 .
7. 如图,将△ABC绕点A按顺时针方向旋转x°到△ADE的位置,使点E首次落在边BC上.已知∠ABC=30°,∠BAE=35°,则x= .
8. 如图,在四边形ABCD中,∠ABC=30°,连接BD,将△DCB绕点C按顺时针方向旋转60°后,点D的对应点恰好与点A重合,得到△ACE.若AB=3,BC=4,求BD的长.
第8题
9. 如图,在Rt△ABC中,∠BAC=90°,AB=AC,D为△ABC内一点,将线段AD绕点A按逆时针方向旋转90°得到AE,连接CE、BD,BD的延长线与CE交于点F.
(1) 求证:BD=CE,BD⊥CE;
(2) 连接AF、CD,若∠BDC=135°,判断AF与CD的位置关系,并说明理由.
第9题
9.1 图形的旋转
1. A 2. (7,4) 3. 75°
4. (1) 如图,△A1B1C1即为所求作 (2) 如图,画出△A2B2C2,连接A1C2、C1C2,则△A1C1C2的面积为4×8-×3×2-×2×8-×4×5=11
5. A 6. (2,2) 7. 50
8. 连接BE.∵ △DCB绕点C按顺时针方向旋转60°得到△ACE,BC=4,∴ CE=BC=4,BD=AE,∠BCE=60°.∴ △BCE是等边三角形.∴ ∠CBE=60°,BE=BC=4.∵ ∠ABC=30°,∴ ∠ABE=∠ABC+∠CBE=90°.∵ AB=3,∴ 在Rt△ABE中,AE==5.∴ BD=5
9. (1) 如图,设AC、BF相交于点O.∵ 线段AD绕点A按逆时针方向旋转90°得到AE,∴ AD=AE,∠DAE=90°.∵ ∠BAC=90°,∴ ∠BAC=∠DAE.∴ ∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.在△ABD和△ACE中,∴ △ABD≌△ACE.∴ BD=CE,∠ABD=∠ACE.又∵ △ABO、△CFO的内角和均为180°,∠AOB=∠COF,∴ ∠DFC=∠BAC=90°.∴ BD⊥CE (2) AF∥CD 理由:如图,过点A作AG⊥BF于点G,AH⊥CE于点H.由(1),得△ABD≌△ACE,BD⊥CE,∴ BD=CE,S△ABD=S△ACE,∠BFE=90°.∴ 易得AG=AH.又∵ AG⊥BF,AH⊥CE,∴ FA平分∠BFE,即∠AFD=∠BFE.∴ ∠AFD=45°.∵ ∠BDC=135°,∠BDC+∠FDC=180°,∴ ∠FDC=45°.∴ ∠AFD=∠FDC.∴ AF∥CD.
1.
如图,将正方形ABCD中的涂色三角形绕点A按顺时针方向旋转90°后,得到的图形为 ( )
2. 如图,在平面直角坐标系中,点A的坐标为(0,3),点B的坐标为(4,0),连接AB.若将△ABO绕点B按顺时针方向旋转90°,得到△A'BO',则点A'的坐标为 .
3. (2024·滨州)将一副三角尺按如图①所示的方式摆放,把三角尺AOB绕公共顶点O按顺时针方向旋转至如图②所示的位置,此时AB∥OD,则∠1的度数为 .
4. 如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(0,4),B(0,2),C(3,2).
(1) 将△ABC以点O为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2) 将△ABC平移后得到△A2B2C2,若点A的对应点A2的坐标为(2,2),求△A1C1C2的面积.
第4题
第5题
5. 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB'C'的位置,连接CC',使得CC'∥AB,则∠BAB'的度数为 ( )
A. 30° B. 35°
C. 40° D. 50°
6. 如图,在平面直角坐标系中,点C的坐标为(-1,0),点A的坐标为(-3,3),将点A绕点C按顺时针方向旋转90°得到点B,则点B的坐标为 .
7. 如图,将△ABC绕点A按顺时针方向旋转x°到△ADE的位置,使点E首次落在边BC上.已知∠ABC=30°,∠BAE=35°,则x= .
8. 如图,在四边形ABCD中,∠ABC=30°,连接BD,将△DCB绕点C按顺时针方向旋转60°后,点D的对应点恰好与点A重合,得到△ACE.若AB=3,BC=4,求BD的长.
第8题
9. 如图,在Rt△ABC中,∠BAC=90°,AB=AC,D为△ABC内一点,将线段AD绕点A按逆时针方向旋转90°得到AE,连接CE、BD,BD的延长线与CE交于点F.
(1) 求证:BD=CE,BD⊥CE;
(2) 连接AF、CD,若∠BDC=135°,判断AF与CD的位置关系,并说明理由.
第9题
9.1 图形的旋转
1. A 2. (7,4) 3. 75°
4. (1) 如图,△A1B1C1即为所求作 (2) 如图,画出△A2B2C2,连接A1C2、C1C2,则△A1C1C2的面积为4×8-×3×2-×2×8-×4×5=11
5. A 6. (2,2) 7. 50
8. 连接BE.∵ △DCB绕点C按顺时针方向旋转60°得到△ACE,BC=4,∴ CE=BC=4,BD=AE,∠BCE=60°.∴ △BCE是等边三角形.∴ ∠CBE=60°,BE=BC=4.∵ ∠ABC=30°,∴ ∠ABE=∠ABC+∠CBE=90°.∵ AB=3,∴ 在Rt△ABE中,AE==5.∴ BD=5
9. (1) 如图,设AC、BF相交于点O.∵ 线段AD绕点A按逆时针方向旋转90°得到AE,∴ AD=AE,∠DAE=90°.∵ ∠BAC=90°,∴ ∠BAC=∠DAE.∴ ∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.在△ABD和△ACE中,∴ △ABD≌△ACE.∴ BD=CE,∠ABD=∠ACE.又∵ △ABO、△CFO的内角和均为180°,∠AOB=∠COF,∴ ∠DFC=∠BAC=90°.∴ BD⊥CE (2) AF∥CD 理由:如图,过点A作AG⊥BF于点G,AH⊥CE于点H.由(1),得△ABD≌△ACE,BD⊥CE,∴ BD=CE,S△ABD=S△ACE,∠BFE=90°.∴ 易得AG=AH.又∵ AG⊥BF,AH⊥CE,∴ FA平分∠BFE,即∠AFD=∠BFE.∴ ∠AFD=45°.∵ ∠BDC=135°,∠BDC+∠FDC=180°,∴ ∠FDC=45°.∴ ∠AFD=∠FDC.∴ AF∥CD.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
