9.3 平行四边形 同步练(含答案)2024-2025学年数学苏科版八年级下册
文档属性
| 名称 | 9.3 平行四边形 同步练(含答案)2024-2025学年数学苏科版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 449.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-03 19:38:22 | ||
图片预览




文档简介
9.3 平行四边形
第1课时 平行四边形的概念与性质
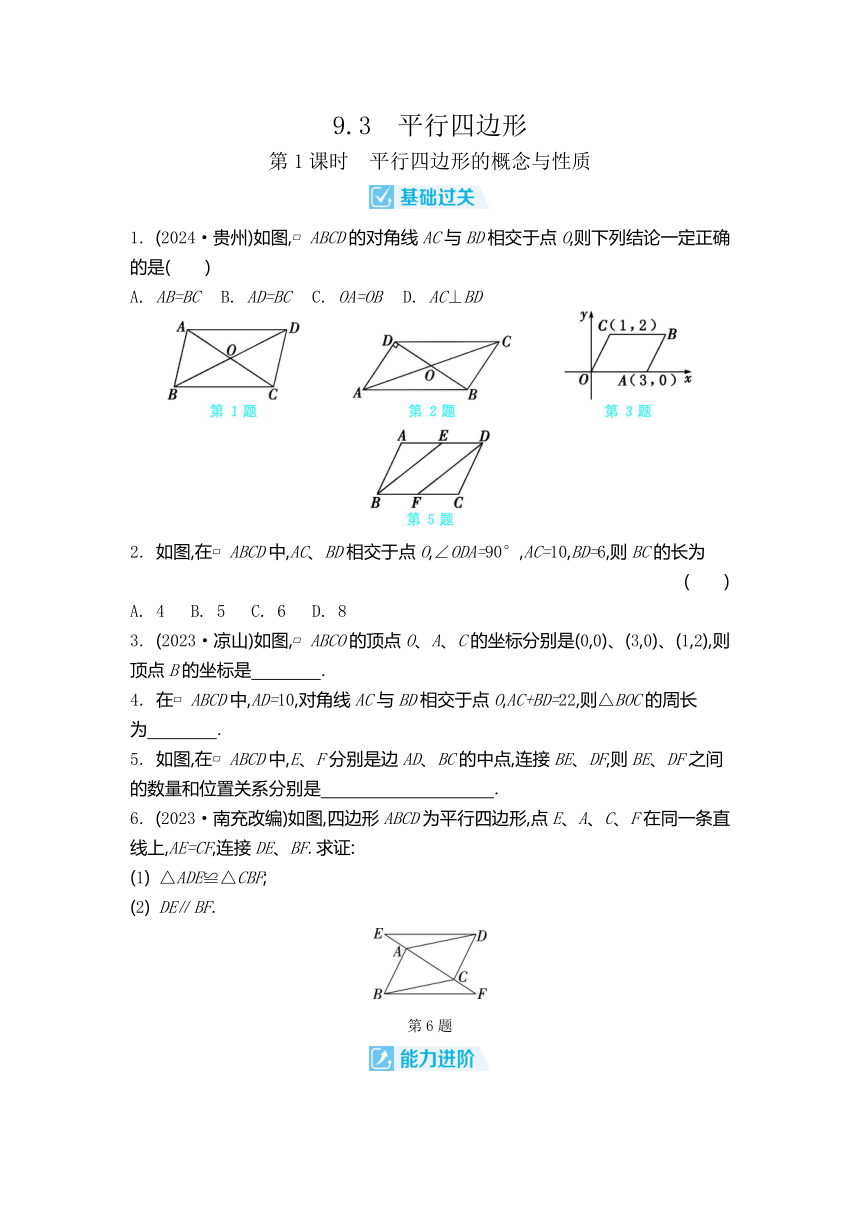
1. (2024·贵州)如图, ABCD的对角线AC与BD相交于点O,则下列结论一定正确的是( )
A. AB=BC B. AD=BC C. OA=OB D. AC⊥BD
2. 如图,在 ABCD中,AC、BD相交于点O,∠ODA=90°,AC=10,BD=6,则BC的长为 ( )
A. 4 B. 5 C. 6 D. 8
3. (2023·凉山)如图, ABCO的顶点O、A、C的坐标分别是(0,0)、(3,0)、(1,2),则顶点B的坐标是 .
4. 在 ABCD中,AD=10,对角线AC与BD相交于点O,AC+BD=22,则△BOC的周长为 .
5. 如图,在 ABCD中,E、F分别是边AD、BC的中点,连接BE、DF,则BE、DF之间的数量和位置关系分别是 .
6. (2023·南充改编)如图,四边形ABCD为平行四边形,点E、A、C、F在同一条直线上,AE=CF,连接DE、BF.求证:
(1) △ADE≌△CBF;
(2) DE∥BF.
第6题
第7题
7. (2024·眉山)如图,在 ABCD中,O为BD的中点,EF经过点O.有下列结论:① AB∥DC;② EO=ED;③ ∠A=∠C;④ S四边形ABOE=S四边形CDOF.其中,一定正确的有 ( )
A. 1个 B. 2个
C. 3个 D. 4个
8. 如图,将 ABCD沿对角线BD折叠,使点A落在点E处.若∠1=56°,∠2=42°,则∠C的度数为 ( )
A. 108° B. 109° C. 110° D. 111°
9. (2023·福建改编)如图,在 ABCD中,O为对角线BD上一点,EF过点O,且分别交AB、CD于点E、F.若OD=BD,OE=10,则EF的长为 .
10. 在平面直角坐标系中, ABCD的顶点A、C、D的坐标分别是(-1,2)、(2,-1)、(3,2),则顶点B的坐标是 .
11. 已知四边形ABCD是平行四边形,AB=6,∠BAD的平分线交直线BC于点E.若CE=2,则 ABCD的周长为 .
12. 如图,在 ABCD中,点E、F分别在AD、BC上,且ED=FB,连接AF、CE.求证:四边形AFCE是平行四边形.
第12题
13. 如图,在 ABCD中,∠BCD=120°,分别延长DC、BC到点E、F,连接AE、BE、AF、DF,使△BCE和△CDF都是等边三角形.
(1) 求证:AE=FA;
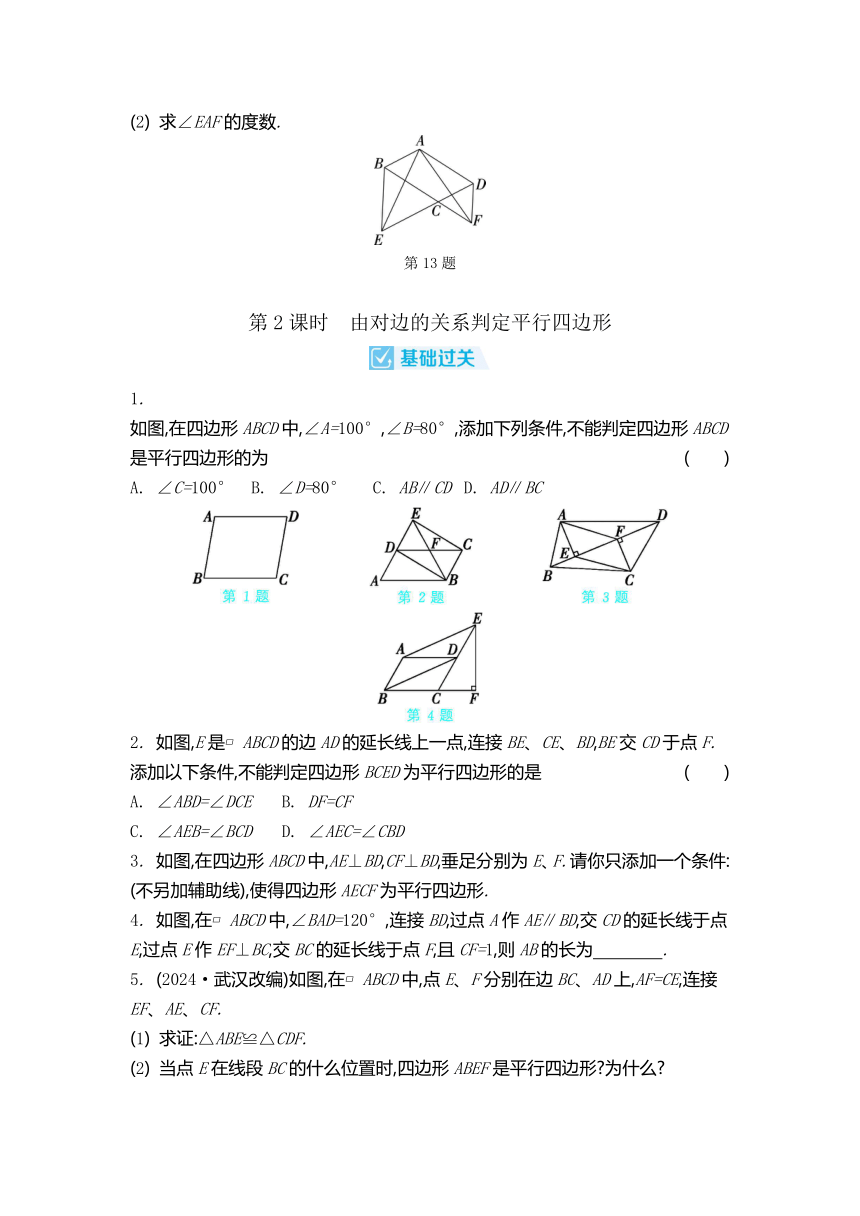
(2) 求∠EAF的度数.
第13题
第2课时 由对边的关系判定平行四边形
1.
如图,在四边形ABCD中,∠A=100°,∠B=80°,添加下列条件,不能判定四边形ABCD是平行四边形的为 ( )
A. ∠C=100° B. ∠D=80° C. AB∥CD D. AD∥BC
2. 如图,E是 ABCD的边AD的延长线上一点,连接BE、CE、BD,BE交CD于点F.添加以下条件,不能判定四边形BCED为平行四边形的是 ( )
A. ∠ABD=∠DCE B. DF=CF
C. ∠AEB=∠BCD D. ∠AEC=∠CBD
3. 如图,在四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.请你只添加一个条件: (不另加辅助线),使得四边形AECF为平行四边形.
4. 如图,在 ABCD中,∠BAD=120°,连接BD,过点A作AE∥BD,交CD的延长线于点E,过点E作EF⊥BC,交BC的延长线于点F,且CF=1,则AB的长为 .
5. (2024·武汉改编)如图,在 ABCD中,点E、F分别在边BC、AD上,AF=CE,连接EF、AE、CF.
(1) 求证:△ABE≌△CDF.
(2) 当点E在线段BC的什么位置时,四边形ABEF是平行四边形 为什么
第5题
6. 在四边形ABCD中,有下列条件:① AB∥CD;② AD∥BC;③ AB=CD;④ AD=BC.从中选择两个条件,使四边形ABCD为平行四边形的选法共有 ( )
A. 3种 B. 4种 C. 5种 D. 6种
第7题
7. (2024·辽宁)如图, ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD,DE、CE相交于点E.若AC=3,BD=5,则四边形OCED的周长为( )
A. 4 B. 6
C. 8 D. 16
8. 在平面直角坐标系中,有四个点O(0,0)、A(3,0)、B(1,1)、C(x,1),则当x的值为 时,以O、A、B、C为顶点的四边形是平行四边形.
9. 如图,在四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,请仅用无刻度的直尺画出△ABD的边BD上的中线(不写作法,保留作图痕迹).
10. 如图,∠DBC=90°,四边形ABCD是平行四边形吗 为什么
第10题
11. 如图,在 ABCD中,E、F分别为边AD、BC的中点,连接BE、EF、DF,对角线AC分别交BE、DF于点G、H.求证:
(1) 四边形BFDE为平行四边形;
(2) AG=CH.
第11题
12. (2024·浙江)如图①,E是 ABCD的边AD上一点(不与点A、D重合),连接CE.用尺规作AF∥CE,其中F是边BC上一点.小明的作法如下:如图②,以点C为圆心,AE长为半径画弧,交BC于点F,连接AF,则AF∥CE.小丽的作法如下:以点A为圆心,CE长为半径画弧,交BC于点F,连接AF,则AF∥CE.小明指出小丽的作法有问题.
(1) 根据小明的作法,求证:AF∥CE;
(2) 指出小丽的作法中存在的问题.
第3课时 由对角线的关系判定平行四边形
1. 在四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:① AB∥CD,AD∥BC;② AB=CD,AD=BC;③ AO=CO,BO=DO;④ AB∥CD,AD=BC.其中,一定能判定这个四边形是平行四边形的共有 ( )
A. 4组 B. 3组 C. 2组 D. 1组
2. 如图,在四边形ABCD中,对角线AC、BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为 ( )
A. 6 B. 12 C. 20 D. 24
3. 用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应假设这个三角形中 ( )
A. 有一个内角大于60° B. 有一个内角小于60°
C. 每一个内角都大于60° D. 每一个内角都小于60°
4. 如图, ABCD的对角线相交于点O,过点O作一条直线,分别交线段AD、BC于点E、F.连接EC、AF,则四边形AFCE是平行四边形,最合适的判定方法是 .
5. 如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,满足∠EAO=∠DCO.
(1) 求证:四边形AECD是平行四边形;
(2) 若AB=BC,CD=5,AC=8,则四边形AECD的面积为 .
第5题
第6题
6. (2024·河北)有这样一道习题:如图,在△ABC中,AB=AC,AE平分△ABC的外角∠CAN,M是AC的中点,连接BM并延长,交AE于点D,连接CD.求证:四边形ABCD是平行四边形.小月的解答过程如下:∵ M是AC的中点,∴ MA=MC.∵ AE平分∠CAN,∴ ∠1=∠2.∵ AB=AC,∴ ∠ABC=∠3.∵ ∠CAN=∠ABC+∠3,∠CAN=∠1+∠2,∠1=∠2,∴ ①.又∵ MA=MC,∠4=∠5,∴ △MAD≌△MCB(②).∴ MD=MB.∴ 四边形ABCD是平行四边形.若小月的解答过程正确,则①②应分别为( )
A. ∠1=∠3,AAS B. ∠1=∠3,ASA C. ∠2=∠3,AAS D. ∠2=∠3,ASA
7. 用反证法证明某一命题的结论“a>b”时,应假设 .
第8题
8. 如图,在四边形ABCD中,AB=CD,对角线AC、BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF、CE.若DE=BF,则有下列结论:① CF=AE;② OE=OF;③ 图中共有四对全等三角形;④ 四边形ABCD是平行四边形.其中,正确的是 (填序号).
9. 用反证法证明:等腰三角形的底角是锐角.
10. 如图,四边形ABCD是平行四边形,E、F是对角线BD上两点,且BF=ED,连接AE、AF、CE、CF.求证:AE∥CF.
第10题
11. 如图①,在 ABCD中,O是对角线AC的中点,EF过点O,与AD、BC分别交于点E、F,GH过点O,与AB、CD分别交于点G、H,连接EG、FG、FH、EH.
(1) 求证:四边形EGFH是平行四边形;
(2) 如图②,若EF∥AB,GH∥BC,在不添加任何辅助线的情况下,请直接写出图②中与四边形AGHD的面积相等的所有平行四边形(四边形AGHD除外).
9.3 平行四边形
第1课时 平行四边形的概念与性质
1. B 2. A 3. (4,2) 4. 21 5. BE=DF,BE∥DF
6. (1) ∵ 四边形ABCD为平行四边形,∴ AD=CB,AD∥CB.∴ ∠DAC=∠BCA.∵ ∠DAC+∠EAD=180°,∠BCA+∠FCB=180°,∴ ∠EAD=∠FCB.在△ADE和△CBF中,∴ △ADE≌△CBF (2) 由(1),得△ADE≌△CBF,∴ ∠E=∠F.∴ DE∥BF
7. C 8. C 9. 20 10. (-2,-1) 11. 20或28
12. ∵ 四边形ABCD是平行四边形,∴ AD∥BC,DC=BA,∠D=∠B.又∵ ED=FB,∴ △EDC≌△FBA.∴ ∠CED=∠AFB.∵ AD∥BC,∴ ∠CED=∠ECB.∴ ∠AFB=∠ECB.∴ AF∥EC.又∵ AE∥FC,∴ 四边形AFCE是平行四边形
13. (1) ∵ 四边形ABCD是平行四边形,∴ ∠ABC=∠ADC,AB=CD,BC=DA.∵ △BCE和△CDF都是等边三角形,∴ BE=BC,FD=CD,∠EBC=∠CDF=60°.∴ AB=FD,BE=DA,∠ABC+∠EBC=∠ADC+∠CDF,即∠ABE=∠FDA.在△ABE和△FDA中,∴ △ABE≌△FDA.∴ AE=FA (2) 由(1),得△ABE≌△FDA,∠EBC=60°,∴ ∠AEB=∠FAD.∵ 四边形ABCD是平行四边形,∠BCD=120°,∴ ∠BAD=∠BCD=120°,AB∥CD.∴ ∠ABF=180°-∠BCD=60°.∴ ∠ABE=∠ABF+∠EBC=120°.∴ ∠AEB+∠BAE=60°.∴ ∠FAD+∠BAE=60°.∴ ∠EAF=∠BAD-(∠FAD+∠BAE)=60°
第2课时 由对边的关系判定平行四边形
1. D 2. C 3. 答案不唯一,如AE=CF 4. 1
5. (1) ∵ 四边形ABCD是平行四边形,∴ AD∥BC,AB=CD,AD=BC,∠B=∠D.∵ AF=CE,∴ AD-AF=BC-CE.∴ DF=BE.在△ABE和△CDF中,∴ △ABE≌△CDF (2) 当E是BC的中点时,四边形ABEF是平行四边形 ∵ E是BC的中点,∴ BE=EC.又∵ AF=EC,∴ BE=AF.∵ BE∥AF,∴ 四边形ABEF是平行四边形
6. B 7. C 8. 4或-2
9. 如图,AF即为所求作
10. 四边形ABCD是平行四边形 ∵ 在Rt△DBC中,∠DBC=90°,∴ DB2+BC2=DC2,即42+(x-5)2=(x-3)2,解得x=8.∴ DC=5,BC=3,AD=3.又∵ AB=5,∴ AD=BC,DC=AB.∴ 四边形ABCD是平行四边形
11. (1) ∵ 四边形ABCD为平行四边形,∴ AD=BC,AD∥BC,即DE∥BF.∵ E、F分别为边AD、BC的中点,∴ DE=AD,BF=BC.∴ DE=BF.∴ 四边形BFDE为平行四边形 (2) 由(1),得AD=BC,AD∥BC,四边形BFDE为平行四边形,∴ ∠EAG=∠FCH,∠AEF=∠CFE,BE∥DF.∴ ∠BEF=∠DFE.∴ ∠AEF-∠BEF=∠CFE-∠DFE,即∠AEG=∠CFH.∵ E、F分别为边AD、BC的中点,∴ AE=AD,CF=BC.∴ AE=CF.在△AEG和△CFH中,∴ △AEG≌△CFH.∴ AG=CH
12. (1) 根据小明的作法,知CF=AE.∵ 四边形ABCD是平行四边形,∴ AD∥BC.又∵ CF=AE,∴ 四边形AFCE是平行四边形.∴ AF∥CE (2) 以点A为圆心,CE长为半径画弧,交BC于点F,此时可能会有两个交点,只有其中一个交点符合题意.∴ 小丽的作法有问题
第3课时 由对角线的关系判定平行四边形
1. B 2. D 3. C 4. 对角线互相平分的四边形是平行四边形
5. (1) 在△AOE和△COD中,∴ △AOE≌△COD.∴ OE=OD.又∵ AO=CO,∴ 四边形AECD是平行四边形
(2) 24 解析:∵ AB=BC,AO=CO,∴ OB⊥AC,即DE⊥AC.∵ 四边形AECD是平行四边形,AC=8,∴ OD=DE,CO=AC=4.∵ CD=5,∴ 在Rt△COD中,OD==3.∴ DE=2OD=6.∴ S四边形AECD=AC·OE+AC·OD=AC·DE=24.
6. D 7. a≤b 8. ①②④
9. 已知:△ABC是等腰三角形,且∠B=∠C.求证:∠B是锐角.证明:假设∠B是直角或钝角.∵ ∠B=∠C,∴ ∠B+∠C≥180°.∴ ∠A+∠B+∠C>180°.这与三角形的内角和定理相矛盾.∴ 假设不成立.∴ ∠B是锐角
10. 连接AC,交BD于点O.∵ 四边形ABCD是平行四边形,∴ OA=OC,OB=OD.∵ BF=ED,∴ BF-OB=ED-OD,即OF=OE.又∵ OA=OC,∴ 四边形AECF是平行四边形.∴ AE∥CF
11. (1) ∵ 四边形ABCD是平行四边形,∴ AD∥BC.∴ ∠EAO=∠FCO.∵ O是AC的中点,∴ OA=OC.在△OAE和△OCF中,∴ △OAE≌△OCF.∴ OE=OF.同理,可得OG=OH,∴ 四边形EGFH是平行四边形 (2) 与四边形AGHD面积相等的平行四边形有 GBCH、 ABFE、 EFCD、 EGFH
第1课时 平行四边形的概念与性质
1. (2024·贵州)如图, ABCD的对角线AC与BD相交于点O,则下列结论一定正确的是( )
A. AB=BC B. AD=BC C. OA=OB D. AC⊥BD
2. 如图,在 ABCD中,AC、BD相交于点O,∠ODA=90°,AC=10,BD=6,则BC的长为 ( )
A. 4 B. 5 C. 6 D. 8
3. (2023·凉山)如图, ABCO的顶点O、A、C的坐标分别是(0,0)、(3,0)、(1,2),则顶点B的坐标是 .
4. 在 ABCD中,AD=10,对角线AC与BD相交于点O,AC+BD=22,则△BOC的周长为 .
5. 如图,在 ABCD中,E、F分别是边AD、BC的中点,连接BE、DF,则BE、DF之间的数量和位置关系分别是 .
6. (2023·南充改编)如图,四边形ABCD为平行四边形,点E、A、C、F在同一条直线上,AE=CF,连接DE、BF.求证:
(1) △ADE≌△CBF;
(2) DE∥BF.
第6题
第7题
7. (2024·眉山)如图,在 ABCD中,O为BD的中点,EF经过点O.有下列结论:① AB∥DC;② EO=ED;③ ∠A=∠C;④ S四边形ABOE=S四边形CDOF.其中,一定正确的有 ( )
A. 1个 B. 2个
C. 3个 D. 4个
8. 如图,将 ABCD沿对角线BD折叠,使点A落在点E处.若∠1=56°,∠2=42°,则∠C的度数为 ( )
A. 108° B. 109° C. 110° D. 111°
9. (2023·福建改编)如图,在 ABCD中,O为对角线BD上一点,EF过点O,且分别交AB、CD于点E、F.若OD=BD,OE=10,则EF的长为 .
10. 在平面直角坐标系中, ABCD的顶点A、C、D的坐标分别是(-1,2)、(2,-1)、(3,2),则顶点B的坐标是 .
11. 已知四边形ABCD是平行四边形,AB=6,∠BAD的平分线交直线BC于点E.若CE=2,则 ABCD的周长为 .
12. 如图,在 ABCD中,点E、F分别在AD、BC上,且ED=FB,连接AF、CE.求证:四边形AFCE是平行四边形.
第12题
13. 如图,在 ABCD中,∠BCD=120°,分别延长DC、BC到点E、F,连接AE、BE、AF、DF,使△BCE和△CDF都是等边三角形.
(1) 求证:AE=FA;
(2) 求∠EAF的度数.
第13题
第2课时 由对边的关系判定平行四边形
1.
如图,在四边形ABCD中,∠A=100°,∠B=80°,添加下列条件,不能判定四边形ABCD是平行四边形的为 ( )
A. ∠C=100° B. ∠D=80° C. AB∥CD D. AD∥BC
2. 如图,E是 ABCD的边AD的延长线上一点,连接BE、CE、BD,BE交CD于点F.添加以下条件,不能判定四边形BCED为平行四边形的是 ( )
A. ∠ABD=∠DCE B. DF=CF
C. ∠AEB=∠BCD D. ∠AEC=∠CBD
3. 如图,在四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.请你只添加一个条件: (不另加辅助线),使得四边形AECF为平行四边形.
4. 如图,在 ABCD中,∠BAD=120°,连接BD,过点A作AE∥BD,交CD的延长线于点E,过点E作EF⊥BC,交BC的延长线于点F,且CF=1,则AB的长为 .
5. (2024·武汉改编)如图,在 ABCD中,点E、F分别在边BC、AD上,AF=CE,连接EF、AE、CF.
(1) 求证:△ABE≌△CDF.
(2) 当点E在线段BC的什么位置时,四边形ABEF是平行四边形 为什么
第5题
6. 在四边形ABCD中,有下列条件:① AB∥CD;② AD∥BC;③ AB=CD;④ AD=BC.从中选择两个条件,使四边形ABCD为平行四边形的选法共有 ( )
A. 3种 B. 4种 C. 5种 D. 6种
第7题
7. (2024·辽宁)如图, ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD,DE、CE相交于点E.若AC=3,BD=5,则四边形OCED的周长为( )
A. 4 B. 6
C. 8 D. 16
8. 在平面直角坐标系中,有四个点O(0,0)、A(3,0)、B(1,1)、C(x,1),则当x的值为 时,以O、A、B、C为顶点的四边形是平行四边形.
9. 如图,在四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,请仅用无刻度的直尺画出△ABD的边BD上的中线(不写作法,保留作图痕迹).
10. 如图,∠DBC=90°,四边形ABCD是平行四边形吗 为什么
第10题
11. 如图,在 ABCD中,E、F分别为边AD、BC的中点,连接BE、EF、DF,对角线AC分别交BE、DF于点G、H.求证:
(1) 四边形BFDE为平行四边形;
(2) AG=CH.
第11题
12. (2024·浙江)如图①,E是 ABCD的边AD上一点(不与点A、D重合),连接CE.用尺规作AF∥CE,其中F是边BC上一点.小明的作法如下:如图②,以点C为圆心,AE长为半径画弧,交BC于点F,连接AF,则AF∥CE.小丽的作法如下:以点A为圆心,CE长为半径画弧,交BC于点F,连接AF,则AF∥CE.小明指出小丽的作法有问题.
(1) 根据小明的作法,求证:AF∥CE;
(2) 指出小丽的作法中存在的问题.
第3课时 由对角线的关系判定平行四边形
1. 在四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:① AB∥CD,AD∥BC;② AB=CD,AD=BC;③ AO=CO,BO=DO;④ AB∥CD,AD=BC.其中,一定能判定这个四边形是平行四边形的共有 ( )
A. 4组 B. 3组 C. 2组 D. 1组
2. 如图,在四边形ABCD中,对角线AC、BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为 ( )
A. 6 B. 12 C. 20 D. 24
3. 用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应假设这个三角形中 ( )
A. 有一个内角大于60° B. 有一个内角小于60°
C. 每一个内角都大于60° D. 每一个内角都小于60°
4. 如图, ABCD的对角线相交于点O,过点O作一条直线,分别交线段AD、BC于点E、F.连接EC、AF,则四边形AFCE是平行四边形,最合适的判定方法是 .
5. 如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,满足∠EAO=∠DCO.
(1) 求证:四边形AECD是平行四边形;
(2) 若AB=BC,CD=5,AC=8,则四边形AECD的面积为 .
第5题
第6题
6. (2024·河北)有这样一道习题:如图,在△ABC中,AB=AC,AE平分△ABC的外角∠CAN,M是AC的中点,连接BM并延长,交AE于点D,连接CD.求证:四边形ABCD是平行四边形.小月的解答过程如下:∵ M是AC的中点,∴ MA=MC.∵ AE平分∠CAN,∴ ∠1=∠2.∵ AB=AC,∴ ∠ABC=∠3.∵ ∠CAN=∠ABC+∠3,∠CAN=∠1+∠2,∠1=∠2,∴ ①.又∵ MA=MC,∠4=∠5,∴ △MAD≌△MCB(②).∴ MD=MB.∴ 四边形ABCD是平行四边形.若小月的解答过程正确,则①②应分别为( )
A. ∠1=∠3,AAS B. ∠1=∠3,ASA C. ∠2=∠3,AAS D. ∠2=∠3,ASA
7. 用反证法证明某一命题的结论“a>b”时,应假设 .
第8题
8. 如图,在四边形ABCD中,AB=CD,对角线AC、BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF、CE.若DE=BF,则有下列结论:① CF=AE;② OE=OF;③ 图中共有四对全等三角形;④ 四边形ABCD是平行四边形.其中,正确的是 (填序号).
9. 用反证法证明:等腰三角形的底角是锐角.
10. 如图,四边形ABCD是平行四边形,E、F是对角线BD上两点,且BF=ED,连接AE、AF、CE、CF.求证:AE∥CF.
第10题
11. 如图①,在 ABCD中,O是对角线AC的中点,EF过点O,与AD、BC分别交于点E、F,GH过点O,与AB、CD分别交于点G、H,连接EG、FG、FH、EH.
(1) 求证:四边形EGFH是平行四边形;
(2) 如图②,若EF∥AB,GH∥BC,在不添加任何辅助线的情况下,请直接写出图②中与四边形AGHD的面积相等的所有平行四边形(四边形AGHD除外).
9.3 平行四边形
第1课时 平行四边形的概念与性质
1. B 2. A 3. (4,2) 4. 21 5. BE=DF,BE∥DF
6. (1) ∵ 四边形ABCD为平行四边形,∴ AD=CB,AD∥CB.∴ ∠DAC=∠BCA.∵ ∠DAC+∠EAD=180°,∠BCA+∠FCB=180°,∴ ∠EAD=∠FCB.在△ADE和△CBF中,∴ △ADE≌△CBF (2) 由(1),得△ADE≌△CBF,∴ ∠E=∠F.∴ DE∥BF
7. C 8. C 9. 20 10. (-2,-1) 11. 20或28
12. ∵ 四边形ABCD是平行四边形,∴ AD∥BC,DC=BA,∠D=∠B.又∵ ED=FB,∴ △EDC≌△FBA.∴ ∠CED=∠AFB.∵ AD∥BC,∴ ∠CED=∠ECB.∴ ∠AFB=∠ECB.∴ AF∥EC.又∵ AE∥FC,∴ 四边形AFCE是平行四边形
13. (1) ∵ 四边形ABCD是平行四边形,∴ ∠ABC=∠ADC,AB=CD,BC=DA.∵ △BCE和△CDF都是等边三角形,∴ BE=BC,FD=CD,∠EBC=∠CDF=60°.∴ AB=FD,BE=DA,∠ABC+∠EBC=∠ADC+∠CDF,即∠ABE=∠FDA.在△ABE和△FDA中,∴ △ABE≌△FDA.∴ AE=FA (2) 由(1),得△ABE≌△FDA,∠EBC=60°,∴ ∠AEB=∠FAD.∵ 四边形ABCD是平行四边形,∠BCD=120°,∴ ∠BAD=∠BCD=120°,AB∥CD.∴ ∠ABF=180°-∠BCD=60°.∴ ∠ABE=∠ABF+∠EBC=120°.∴ ∠AEB+∠BAE=60°.∴ ∠FAD+∠BAE=60°.∴ ∠EAF=∠BAD-(∠FAD+∠BAE)=60°
第2课时 由对边的关系判定平行四边形
1. D 2. C 3. 答案不唯一,如AE=CF 4. 1
5. (1) ∵ 四边形ABCD是平行四边形,∴ AD∥BC,AB=CD,AD=BC,∠B=∠D.∵ AF=CE,∴ AD-AF=BC-CE.∴ DF=BE.在△ABE和△CDF中,∴ △ABE≌△CDF (2) 当E是BC的中点时,四边形ABEF是平行四边形 ∵ E是BC的中点,∴ BE=EC.又∵ AF=EC,∴ BE=AF.∵ BE∥AF,∴ 四边形ABEF是平行四边形
6. B 7. C 8. 4或-2
9. 如图,AF即为所求作
10. 四边形ABCD是平行四边形 ∵ 在Rt△DBC中,∠DBC=90°,∴ DB2+BC2=DC2,即42+(x-5)2=(x-3)2,解得x=8.∴ DC=5,BC=3,AD=3.又∵ AB=5,∴ AD=BC,DC=AB.∴ 四边形ABCD是平行四边形
11. (1) ∵ 四边形ABCD为平行四边形,∴ AD=BC,AD∥BC,即DE∥BF.∵ E、F分别为边AD、BC的中点,∴ DE=AD,BF=BC.∴ DE=BF.∴ 四边形BFDE为平行四边形 (2) 由(1),得AD=BC,AD∥BC,四边形BFDE为平行四边形,∴ ∠EAG=∠FCH,∠AEF=∠CFE,BE∥DF.∴ ∠BEF=∠DFE.∴ ∠AEF-∠BEF=∠CFE-∠DFE,即∠AEG=∠CFH.∵ E、F分别为边AD、BC的中点,∴ AE=AD,CF=BC.∴ AE=CF.在△AEG和△CFH中,∴ △AEG≌△CFH.∴ AG=CH
12. (1) 根据小明的作法,知CF=AE.∵ 四边形ABCD是平行四边形,∴ AD∥BC.又∵ CF=AE,∴ 四边形AFCE是平行四边形.∴ AF∥CE (2) 以点A为圆心,CE长为半径画弧,交BC于点F,此时可能会有两个交点,只有其中一个交点符合题意.∴ 小丽的作法有问题
第3课时 由对角线的关系判定平行四边形
1. B 2. D 3. C 4. 对角线互相平分的四边形是平行四边形
5. (1) 在△AOE和△COD中,∴ △AOE≌△COD.∴ OE=OD.又∵ AO=CO,∴ 四边形AECD是平行四边形
(2) 24 解析:∵ AB=BC,AO=CO,∴ OB⊥AC,即DE⊥AC.∵ 四边形AECD是平行四边形,AC=8,∴ OD=DE,CO=AC=4.∵ CD=5,∴ 在Rt△COD中,OD==3.∴ DE=2OD=6.∴ S四边形AECD=AC·OE+AC·OD=AC·DE=24.
6. D 7. a≤b 8. ①②④
9. 已知:△ABC是等腰三角形,且∠B=∠C.求证:∠B是锐角.证明:假设∠B是直角或钝角.∵ ∠B=∠C,∴ ∠B+∠C≥180°.∴ ∠A+∠B+∠C>180°.这与三角形的内角和定理相矛盾.∴ 假设不成立.∴ ∠B是锐角
10. 连接AC,交BD于点O.∵ 四边形ABCD是平行四边形,∴ OA=OC,OB=OD.∵ BF=ED,∴ BF-OB=ED-OD,即OF=OE.又∵ OA=OC,∴ 四边形AECF是平行四边形.∴ AE∥CF
11. (1) ∵ 四边形ABCD是平行四边形,∴ AD∥BC.∴ ∠EAO=∠FCO.∵ O是AC的中点,∴ OA=OC.在△OAE和△OCF中,∴ △OAE≌△OCF.∴ OE=OF.同理,可得OG=OH,∴ 四边形EGFH是平行四边形 (2) 与四边形AGHD面积相等的平行四边形有 GBCH、 ABFE、 EFCD、 EGFH
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
