9.4 矩形、菱形、正方形 同步练(5课时、含答案) 2024-2025学年数学苏科版八年级下册
文档属性
| 名称 | 9.4 矩形、菱形、正方形 同步练(5课时、含答案) 2024-2025学年数学苏科版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 406.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-03 00:00:00 | ||
图片预览




文档简介
9.4 矩形、菱形、正方形
第1课时 矩形的概念与性质
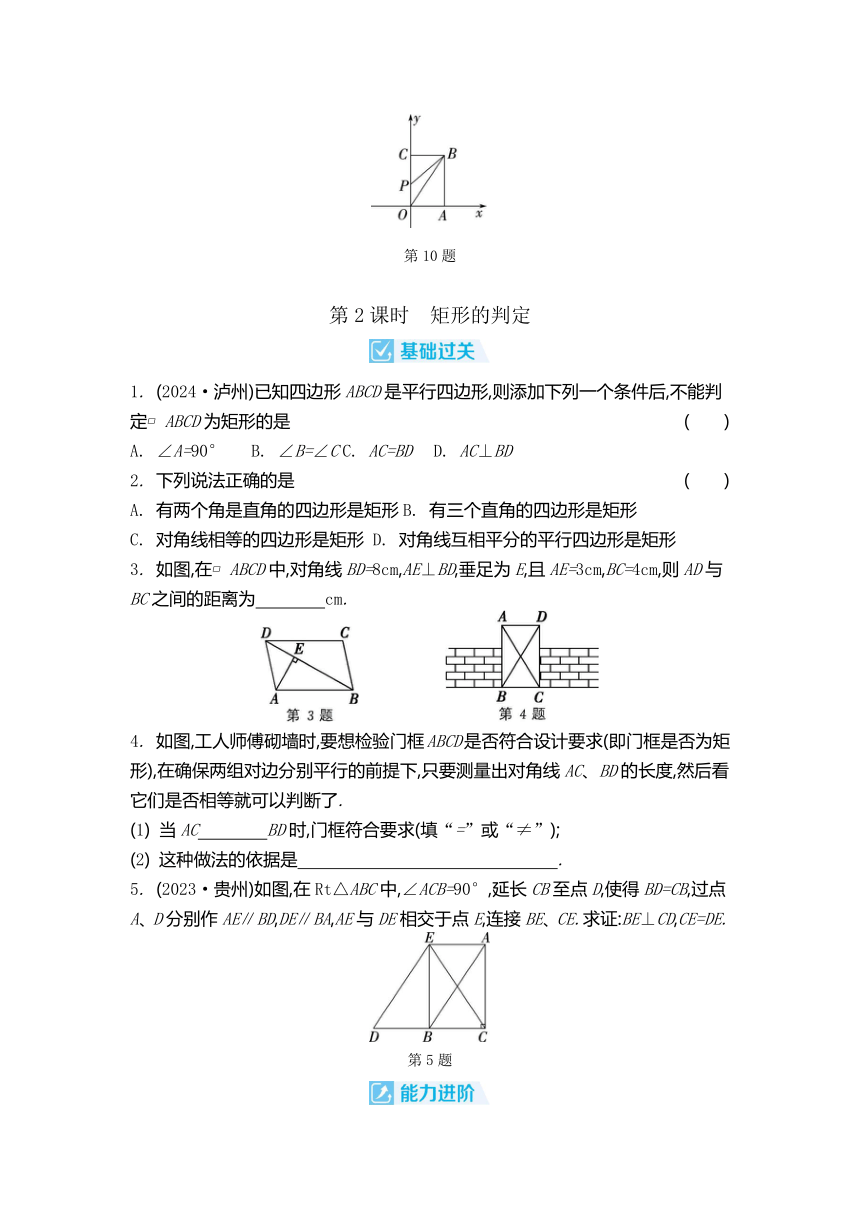
1. (2024·成都)如图,在矩形ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是 ( )
A. AB=AD B. AC⊥BD C. AC=BD D. ∠ACB=∠ACD
2. 在矩形ABCD中,O是BC的中点,∠AOD=90°,矩形ABCD的周长为20cm,则AB的长为 ( )
A. 1cm B. 2cm C. cm D. cm
3. 如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的点A'处.若∠DBC=24°,则∠A'EB的度数为 .
4. 如图,线段BC为等腰三角形ABC的底边,矩形ADBE的对角线AB与DE交于点O.若OD=2,则AC的长为 .
5. 如图,在矩形ABCD中,E是AD的中点,延长CE、BA交于点F,连接AC、DF.
(1) 求证:四边形ACDF是平行四边形;
(2) 当CF平分∠BCD时,写出BC与CD之间的数量关系,并说明理由.
第5题
第6题
6. 如图,在矩形ABCD中,E是BA的延长线上一点,F是CE上一点,连接AC、AF.若AC=AF=EF,∠ACB=21°,则∠ECD的度数为 ( )
A. 7° B. 21°
C. 23° D. 24°
7. (2023·哈尔滨)矩形ABCD的对角线AC、BD相交于点O,点F在矩形ABCD的边上,连接OF.若∠ADB=38°,∠BOF=30°,则∠AOF的度数为 .
第8题
8. 如图,在矩形ABCD中,AB=6,BC=10,以点B为圆心,BC的长为半径画弧,交AD于点E,连接BE,再分别以点C、E为圆心,大于CE的长为半径画弧,两弧交于点F,作射线BF交CD于点G,则CG的长为 .
9. (2023·宿迁改编)如图,在矩形ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F.
(1) 求证:AE=CF;
(2) 当∠ADB=30°时,连接AF、CE,在不添加任何辅助线的情况下,图中面积等于矩形ABCD面积的的三角形是 .
第9题
10. 如图,在矩形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),a、b满足+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
(1) 点B的坐标为 .当点P移动3.5秒时,点P的坐标为 .
(2) 当点P到x轴的距离为4个单位长度时,求点P的移动时间.
(3) 当以O、B、P为顶点的三角形的面积为10时,求点P的移动时间.
第10题
第2课时 矩形的判定
1. (2024·泸州)已知四边形ABCD是平行四边形,则添加下列一个条件后,不能判定 ABCD为矩形的是 ( )
A. ∠A=90° B. ∠B=∠C C. AC=BD D. AC⊥BD
2. 下列说法正确的是 ( )
A. 有两个角是直角的四边形是矩形 B. 有三个直角的四边形是矩形
C. 对角线相等的四边形是矩形 D. 对角线互相平分的平行四边形是矩形
3. 如图,在 ABCD中,对角线BD=8cm,AE⊥BD,垂足为E,且AE=3cm,BC=4cm,则AD与BC之间的距离为 cm.
4. 如图,工人师傅砌墙时,要想检验门框ABCD是否符合设计要求(即门框是否为矩形),在确保两组对边分别平行的前提下,只要测量出对角线AC、BD的长度,然后看它们是否相等就可以判断了.
(1) 当AC BD时,门框符合要求(填“=”或“≠”);
(2) 这种做法的依据是 .
5. (2023·贵州)如图,在Rt△ABC中,∠ACB=90°,延长CB至点D,使得BD=CB,过点A、D分别作AE∥BD,DE∥BA,AE与DE相交于点E,连接BE、CE.求证:BE⊥CD,CE=DE.
第5题
第6题
6. 如图,在 ABCD中,对角线AC、BD相交于点O,M、N是BD上两点,BM=DN,连接AM、MC、CN、NA,添加一个条件,使四边形AMCN是矩形,这个条件可以是 ( )
A. OM=AC B. MB=MO
C. BD⊥AC D. ∠AMB=∠CND
第8题
7. 设AB、CD、EF是同一平面内三条互相平行的直线.已知AB与CD之间的距离是12cm,EF与CD之间的距离是5cm,则AB与EF之间的距离是 .
8. 如图,在矩形ABCD中,AB=6,AD=8,且有一点P从点B出发,沿着BD往点D移动,过点P作AB的垂线,交AB于点E,过点P作AD的垂线,交AD于点F,连接EF,则EF长的最小值为 .
9. (2024·贵州)如图,四边形ABCD的对角线AC与BD相交于点O,AD∥BC,∠ABC=90°, .有以下条件:① AB∥CD;② AD=BC.
(1) 请从①②中任选1个填到横线上(填序号),求证:四边形ABCD是矩形;
(2) 在(1)的条件下,若AB=3,AC=5,求四边形ABCD的面积.
第9题
10. 如图,AC=AB,AD=AE,DE=BC,∠BAD=∠CAE.求证:四边形BCDE是矩形(用两种不同的矩形判定方法证明).
第10题
第3课时 菱形的概念与性质
1.
如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论错误的是 ( )
A. AB=AD B. AC⊥BD C. AC=BD D. ∠DAC=∠BAC
2. (2023·湘潭)如图,在菱形ABCD中,连接AC、BD.若∠1=20°,则∠2的度数为 ( )
A. 20° B. 60° C. 70° D. 80°
3. 如图,菱形ABCD的对角线AC、BD交于点O,E为AD的中点,连接OE.若OE=3,则菱形ABCD的周长为 .
4. 如图,在菱形ABCD中,对角线AC、BD交于点O,过点A作AH⊥BC于点H.已知BO=8,S菱形ABCD=96,则AH的长为 .
5. 如图,四边形ABCD为菱形,E为对角线AC上的一个动点(不与点A、C重合),连接DE并延长,交射线AB于点F,连接BE.求证:
(1) △DCE≌△BCE;
(2) ∠AFD=∠EBC.
第5题
第6题
6. 如图,在菱形ABCD中,连接AC、BD,AB=5,AC=6,过点D作DE⊥AB,交BA的延长线于点E,则线段DE的长为 ( )
A. B.
C. 4 D.
7. 如图,菱形ABCD的对角线AC、BD相交于点O,AC=4,BD=16,将△ABO沿AC方向平移,得到△A'B'O'.当点A'与点C重合时,点A与点B'之间的距离为 ( )
A. 6 B. 8 C. 10 D. 12
8. 如图,若菱形ABCD的顶点A、B的坐标分别为(3,0)、(-2,0),点D在y轴正半轴上,则点C的坐标是 .
9. 如图,在菱形ABCD中,AC交BD于点O,DE⊥BC于点E,连接OE.若∠ABC=140°,则∠OED的度数为 .
10. (2023·凉山)如图,在 ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB,交AC于点E.
(1) 求证:AC⊥BD;
(2) 若AB=10,AC=16,求OE的长.
第10题
11. 如图,在菱形ABCD中,对角线AC、BD交于点O,过点D作对角线BD的垂线,交BA的延长线于点E.
(1) 求证:四边形ACDE是平行四边形;
(2) 若AC=16,BD=12,求△ADE的周长.
第11题
第4课时 菱形的判定
1. (2024·通辽)如图, ABCD的对角线AC、BD相交于点O.添加下列一个条件后,不能证明 ABCD是菱形的为 ( )
A. ∠BAC=∠BCA B. ∠ABD=∠CBD C. OA2+OB2=AD2 D. AD2+OA2=OD2
2. 下列说法中,不正确的是 ( )
A. 四边相等的四边形是菱形 B. 对角线垂直的平行四边形是菱形
C. 菱形的对角线互相垂直且相等 D. 菱形的邻边相等
3. (2023·深圳)如图,在 ABCD中,AB=4,BC=6,将线段AB水平向右平移a个单位长度得到线段EF,当a的值为 时,四边形ECDF为菱形.
4. 把一张矩形纸片按如图所示的方法对折两次,然后剪下三角形纸片并展开,得到的图形一定是 (填写一个特殊的平行四边形).
5. (2023·张家界)如图,点A、D、C、B在同一条直线上,且AD=BC,AE=BF,CE=DF,连接DE、CF.
(1) 求证:AE∥BF;
(2) 若DF=FC,求证:四边形DECF是菱形.
第5题
6. 一个平行四边形的一条边的长为,两条对角线长分别为4和2,这个平行四边形是 ( )
A. 矩形 B. 菱形
C. 一般平行四边形 D. 有一个内角是60°的平行四边形
7. (2024·上海)已知四边形ABCD为矩形,过点A、C作对角线BD的垂线,过点B、D作对角线AC的垂线.如果四条垂线段首尾相连拼成一个四边形,那么这个四边形为 ( )
A. 菱形 B. 矩形 C. 直角梯形 D. 等腰梯形
第8题
8. (2023·聊城)如图,在 ABCD中,BC的垂直平分线EO交AD于点E,交BC于点O,连接BE、CE,过点C作CF∥BE,交EO的延长线于点F,连接BF.若AD=8,CE=5,则四边形BFCE的面积为 .
9. 四边形的四条边长分别为a、b、c、d,且满足条件a2+b2+c2+d2=ab+bc+cd+da,则此四边形一定是 .
10. 如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线分别交AD、BC、BD于点M、N、O,连接BM、DN.
(1) 求证:四边形BNDM是菱形;
(2) 若BD=24,MN=10,求菱形BNDM的周长.
第10题
11. 将两张长为8、宽为4的矩形纸片按如图所示的方式叠放.
(1) 判断四边形AGCH的形状,并说明理由;
(2) 求四边形AGCH的面积.
第11题
第5课时 正方形的概念、性质与判定
1.
如图,一个四边形顺次添加下列条件中的三个条件便得到正方形:a. 两组对边分别相等;b. 一组对边平行且相等;c. 一组邻边相等;d. 一个角是直角.顺次添加的条件:① a→c→d;② b→d→c;③ a→b→c.其中,正确的是 ( )
A. 仅① B. 仅③ C. ①② D. ②③
2. 如图,在正方形ABCD中,AB=6,G是BC的中点.将△ABG沿直线AG折叠得到△AFG,延长GF,交DC于点E,则DE的长是 ( )
A. 1 B. 1.5 C. 2 D. 2.5
3. (2024·兴安盟改编)如图,正方形ABCD的对角线AC与BD相交于点O,E是边BC上一点,F是BD上一点,连接DE、EF.若△DEF与△DEC关于直线DE对称,则∠FEB= .
4. 如图,正方形ABCD的对角线AC、BD交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F.若BD=4,则AF的长为 .
5. (2023·绍兴)如图,在正方形ABCD中,G是对角线BD上的一点(不与点B、D重合),GE⊥CD,GF⊥BC,垂足分别为E、F.连接EF、AG,延长AG交EF于点H.
(1) 求证:∠DAG=∠EGH;
(2) 判断AH与EF是否垂直,并说明理由.
第5题
第6题
6. (2023·重庆A卷)如图,在正方形ABCD中,点E、F分别在BC、CD上,连接AE、AF、EF,∠EAF=45°.若∠BAE=α,则∠FEC一定等于 ( )
A. 2α
B. 90°-2α
C. 45°-α
D. 90°-α
7. (2024·重庆A卷改编)如图,正方形ABCD的边CD上有一点E,连接AE,将AE绕点E按逆时针方向旋转90°,得到FE,连接CF并延长,与AB的延长线交于点G,则∠G的度数为( )
A. 40° B. 45° C. 50° D. 60°
8. (2023·重庆B卷改编)如图,在正方形ABCD中,O为对角线AC的中点,E为正方形内一点,连接BE,BE=BA,连接CE并延长,与∠ABE的平分线交于点F,连接OF.若AB=1,则OF的长为 .
9. 如图,过直线AP上一点A作正方形ABCD,∠PAD=30°,若以点B为圆心,AB的长为半径作弧,与AP交于点A、M,分别以点A、M为圆心,AM的长为半径作弧,两弧交于点E,连接ED,则∠ADE的度数为 .
10. 如图,在正方形ABCD中,E、F、G、H分别是各边上的点,且AE=BF=CG=DH.求证:
(1) △AHE≌△BEF;
(2) 四边形EFGH是正方形.
第10题
11. 如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
(1) 求证:BQ=AP;
(2) 在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段的长度差等于PQ的长.
第11题
9.4 矩形、菱形、正方形
第1课时 矩形的概念与性质
1. C 2. D 3. 57° 4. 4
5. (1) ∵ 四边形ABCD是矩形,∴ AB∥CD,即FA∥CD.∴ ∠FAE=∠CDE.∵ E是AD的中点,∴ AE=DE.又∵ ∠FEA=∠CED,∴ △FAE≌△CDE.∴ FA=CD.∴ 四边形ACDF是平行四边形 (2) BC=2CD 理由:∵ 四边形ABCD是矩形,∴ AD=BC,∠ADC=∠BCD=90°.∵ CF平分∠BCD,∴ ∠DCE=45°.∴ 在Rt△CDE中,∠DCE=∠DEC=45°.∴ CD=DE.∵ E是AD的中点,∴ AD=2DE=2CD.∴ BC=2CD.
6. C 7. 46°或106°
8. 解析:连接EG.设CG=x.根据作图过程,可知BC=BE=10,BF是∠EBC的平分线,证△EBG≌△CBG,得EG=CG=x.先在Rt△BAE中,利用勾股定理求得AE=8,从而可得DE=2,再在Rt△EDG中,利用勾股定理,构造方程22+(6-x)2=x2,由此可求出CG的长.
9. (1) ∵ 四边形ABCD是矩形,∴ AB=CD,AB∥CD.∴ ∠ABE=∠CDF.∵ AE⊥BD,CF⊥BD,∴ ∠AEB=∠CFD=90°.在△ABE和△CDF中,∴ △ABE≌△CDF.∴ AE=CF (2) △ABE、△CDF、△BCE、△ADF
10. (1) (4,6) (1,6) (2) 由题意,可得OA=BC=4,OC=AB=6.当点P到x轴的距离为4个单位长度时,分两种情况讨论:① 当点P在OC上时,OP=4.∴ 点P的移动时间为4÷2=2(秒).② 当点P在AB上时,AP=4.∴ 点P的移动时间为(6+4+6-4)÷2=6(秒).综上所述,点P的移动时间为2秒或6秒 (3) ① 当点P在OC上时,如图①.由题意,得BC·OP=10,即×4OP=10.∴ OP=5.∴ 点P的移动时间为5÷2=(秒).② 当点P在BC上时,如图②.由题意,得OC·PB=10,即×6PB=10.∴ BP=.∴ CP=.∴ 点P的移动时间为6+÷2=(秒).③ 当点P在AB上时,如图③.由题意,得BP·BC=10,即BP×4=10.∴ BP=5.∴ 点P的移动时间为(6+4+5)÷2=(秒).④ 当点P在OA上时,如图④.由题意,得OP·AB=10,即OP×6=10.∴ OP=.∴ 点P的移动时间为6+4+6+4-÷2=(秒).综上所述,点P的移动时间为秒或秒或秒或秒
第2课时 矩形的判定
1. D 2. B 3. 6 4. (1) = (2) 对角线相等的平行四边形是矩形
5. ∵ AE∥BD,DE∥BA,∴ 四边形ABDE是平行四边形.∴ AE=BD,AB=DE.∵ BD=BC,∴ AE=BC.∵ AE∥BD,即AE∥BC,∴ 四边形AEBC是平行四边形.∵ ∠ACB=90°,∴ 四边形AEBC是矩形.∴ ∠EBC=90°,AB=CE.∴ BE⊥CD,CE=DE
6. A 7. 7cm或17cm
8. 解析:根据题意,得四边形AEPF为矩形,连接AP,则AP=EF,将求EF长的最小值转化成求AP长的最小值.由于垂线段最短,因此当AP⊥BD时,AP的长取得最小值.此时 S△ABD=AB·AD=BD·AP,得AP=,∴ EF长的最小值为.
9. (1) 选择不唯一,如选择① ∵ AD∥BC,AB∥CD,∴ 四边形ABCD是平行四边形.∵ ∠ABC=90°,∴ 四边形ABCD是矩形 (2) ∵ ∠ABC=90°,AB=3,AC=5,∴ BC==4.∵ 四边形ABCD是矩形,∴ 四边形ABCD的面积=AB·BC=3×4=12
10. 证法一:∵ ∠BAD=∠CAE,∴ ∠BAD-∠BAC=∠CAE-∠BAC,即∠CAD=∠BAE.又∵ AC=AB,AD=AE,∴ △CAD≌△BAE.∴ ∠CDA=∠BEA,CD=BE.又∵ DE=BC,∴ 四边形BCDE是平行四边形.∴ BE∥CD.∴ ∠CDE+∠BED=180°.∵ AD=AE,∴ ∠ADE=∠AED.∴ ∠CDA-∠ADE=∠BEA-∠AED,即∠CDE=∠BED.∴ ∠CDE=∠BED=90°.∴ 四边形BCDE是矩形 证法二:同证法一,得△CAD≌△BAE,∴ CD=BE.又∵ DE=BC,∴ 四边形BCDE是平行四边形.连接BD、CE.∵ AB=AC,∠BAD=∠CAE,AD=AE,∴ △BAD≌△CAE.∴ BD=CE.∴ 四边形BCDE是矩形
第3课时 菱形的概念与性质
1. C 2. C 3. 24 4.
5. (1) ∵ 四边形ABCD是菱形,∴ CD=CB,∠DCE=∠BCE.在△DCE和△BCE中,∴ △DCE≌△BCE (2) ∵ 四边形ABCD是菱形,∴ DC∥AF.∴ ∠CDF=∠AFD.∵ △DCE≌△BCE,∴ ∠CDF=∠EBC.∴ ∠AFD=∠EBC
6. D 7. C 8. (-5,4) 9. 20°
10. (1) ∵ ∠CAB=∠ACB,∴ AB=CB.∵ 四边形ABCD是平行四边形,∴ ABCD是菱形.∴ AC⊥BD (2) 设OE=x.∵ ABCD是菱形,AC=16,∴ OA=AC=8.∵ AC⊥BD,∴ ∠AOB=∠BOE=90°.∴ 在Rt△AOB中,OB===6.∴ 在Rt△EOB中,BE2=OE2+OB2=x2+62.∵ BE⊥AB,∴ ∠EBA=90°.∴ 在Rt△ABE中,BE2=AE2-AB2=(8+x)2-102.∴ x2+62=(8+x)2-102,解得x=.∴ OE的长为
11. (1) ∵ 四边形ABCD是菱形,∴ AB∥CD,AC⊥BD.∴ AE∥CD.又∵ DE⊥BD,∴ DE∥AC.∴ 四边形ACDE是平行四边形 (2) ∵ 四边形ABCD是菱形,AC=16,BD=12,∴ AC⊥BD,AD=CD,AO=AC=8,DO=BD=6.∴ 在Rt△AOD中,AD==10.∴ CD=10.∵ 四边形ACDE是平行四边形,∴ AE=CD=10,DE=AC=16.∴ △ADE的周长为AD+AE+DE=36
第4课时 菱形的判定
1. D 2. C 3. 2 4. 菱形
5. (1) ∵ AD=BC,∴ AD+CD=BC+CD,即AC=BD.在△AEC和△BFD中,∴ △AEC≌△BFD.∴ ∠A=∠B.∴ AE∥BF (2) ∵ △AEC≌△BFD,∴ ∠ECA=∠FDB.∴ EC∥DF.∵ EC=DF,∴ 四边形DECF是平行四边形.∵ DF=FC,∴ 四边形DECF是菱形
6. B 7. A
8. 24 解析:由平行四边形的性质,得BC=AD=8.∵ EF垂直平分BC,∴ EF⊥BC,OC=OB=BC=4.∴ 在Rt△EOC中,由勾股定理,得OE=3.证△OCF≌△OBE,得OE=OF=3,由此可说明四边形BFCE为菱形,∴ S四边形BFCE=BC·EF=24.
9. 菱形
10. (1) ∵ AD∥BC,∴ ∠DMO=∠BNO.∵ MN是对角线BD的垂直平分线,∴ OD=OB,MN⊥BD.在△MOD和△NOB中,∴ △MOD≌△NOB.∴ OM=ON.∵ OD=OB,∴ 四边形BNDM是平行四边形.∵ MN⊥BD,∴ 四边形BNDM是菱形 (2) ∵ 四边形BNDM是菱形,BD=24,MN=10,∴ BM=BN=DM=DN,OB=BD=12,OM=MN=5.∵ MN⊥BD,∴ ∠BOM=90°.在Rt△BOM中,由勾股定理,得BM===13.∴ 菱形BNDM的周长=4BM=4×13=52
11. (1) 四边形AGCH是菱形 理由:∵ 四边形ABCD和四边形AFCE是矩形,∴ ∠B=∠F=90°,AD∥BC,AF∥CE.∴ 四边形AGCH是平行四边形.∵ S AGCH=GC·AB=AG·CF,AB=CF=4,∴ GC=AG.∴ 四边形AGCH是菱形. (2) 由(1)可知,GC=AG.设GC=AG=x,则BG=8-x.∵ 在矩形ABCD中,∠B=90°,AB=4,∴ 在Rt△ABG中,由勾股定理,得42+(8-x)2=x2,解得x=5.∴ GC=5.∴ S菱形AGCH=GC·AB=5×4=20
第5课时 正方形的概念、性质与判定
1. C 2. C 3. 45° 4.
5. (1) ∵ 四边形ABCD是正方形,∴ ∠ADC=90°.∵ GE⊥CD,∴ ∠GEC=90°.∴ ∠ADC=∠GEC.∴ AD∥GE.∴ ∠DAG=∠EGH (2) AH⊥EF 理由:如图,连接GC,交EF于点O. ∵ 在正方形ABCD中,BD是对角线,∴ ∠BCD=90°,∠ADG=∠CDG,AD=CD.∵ DG=DG,∴ △ADG≌△CDG.∴ ∠DAG=∠DCG.∵ GE⊥CD,GF⊥BC,∴ ∠GFC=∠GEC=90°=∠BCD.∴ 四边形FCEG为矩形.∴ GC=EF,OE=EF,OC=GC.∴ OE=OC.∴ ∠OEC=∠OCE.∴ ∠DAG=∠OEC.由(1),得∠DAG=∠EGH,∴ ∠EGH=∠OEC.∵ ∠GEC=∠OEC+∠GEH=90°,∴ ∠EGH+∠GEH=90°.∴ ∠GHE=90°.∴ AH⊥EF.
6. A 解析:延长FD至点G,使得DG=BE,连接AG,可证△ADG≌△ABE.∴ ∠G=∠AEB=90°-α,AG=AE,∠GAD=∠EAB.∴ 易得∠GAF=∠EAF=45°.又∵ AF=AF,∴ △GAF≌△EAF.∴ ∠AEF=∠G=90°-α.∴ ∠FEC=180°-∠AEB-∠AEF=2α.
7. B 8. 9. 15°或45°
10. (1) ∵ 四边形ABCD为正方形,∴ AB=BC=CD=AD,∠A=∠B=∠C=∠D=90°.∵ AE=BF=CG=DH,∴ BE=CF=DG=AH.∴ △AHE≌△BEF (2) ∵ AE=BF=CG=DH,AH=BE=CF=DG,∠A=∠B=∠C=∠D=90°,∴ △AEH≌△BFE≌△CGF≌△DHG.∴ EH=FE=GF=HG,∠EHA=∠HGD.∴ 四边形EFGH是菱形.∵ ∠D=90°,∴ ∠HGD+∠GHD=90°.∴ ∠EHA+∠GHD=90°.∴ ∠EHG=90°.∴ 四边形EFGH是正方形
11. (1) ∵ 四边形ABCD是正方形,∴ BA=DA,∠BAD=90°,即∠BAQ+∠DAP=90°.∵ DP⊥AQ,∴ ∠ADP+∠DAP=90°.∴ ∠BAQ=∠ADP.∵ AQ⊥BE,DP⊥AQ,∴ ∠AQB=∠DPA=90°.∴ △AQB≌△DPA.∴ BQ=AP (2) AQ-AP=PQ,AQ-BQ=PQ,DP-AP=PQ,DP-BQ=PQ
第1课时 矩形的概念与性质
1. (2024·成都)如图,在矩形ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是 ( )
A. AB=AD B. AC⊥BD C. AC=BD D. ∠ACB=∠ACD
2. 在矩形ABCD中,O是BC的中点,∠AOD=90°,矩形ABCD的周长为20cm,则AB的长为 ( )
A. 1cm B. 2cm C. cm D. cm
3. 如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的点A'处.若∠DBC=24°,则∠A'EB的度数为 .
4. 如图,线段BC为等腰三角形ABC的底边,矩形ADBE的对角线AB与DE交于点O.若OD=2,则AC的长为 .
5. 如图,在矩形ABCD中,E是AD的中点,延长CE、BA交于点F,连接AC、DF.
(1) 求证:四边形ACDF是平行四边形;
(2) 当CF平分∠BCD时,写出BC与CD之间的数量关系,并说明理由.
第5题
第6题
6. 如图,在矩形ABCD中,E是BA的延长线上一点,F是CE上一点,连接AC、AF.若AC=AF=EF,∠ACB=21°,则∠ECD的度数为 ( )
A. 7° B. 21°
C. 23° D. 24°
7. (2023·哈尔滨)矩形ABCD的对角线AC、BD相交于点O,点F在矩形ABCD的边上,连接OF.若∠ADB=38°,∠BOF=30°,则∠AOF的度数为 .
第8题
8. 如图,在矩形ABCD中,AB=6,BC=10,以点B为圆心,BC的长为半径画弧,交AD于点E,连接BE,再分别以点C、E为圆心,大于CE的长为半径画弧,两弧交于点F,作射线BF交CD于点G,则CG的长为 .
9. (2023·宿迁改编)如图,在矩形ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F.
(1) 求证:AE=CF;
(2) 当∠ADB=30°时,连接AF、CE,在不添加任何辅助线的情况下,图中面积等于矩形ABCD面积的的三角形是 .
第9题
10. 如图,在矩形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),a、b满足+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
(1) 点B的坐标为 .当点P移动3.5秒时,点P的坐标为 .
(2) 当点P到x轴的距离为4个单位长度时,求点P的移动时间.
(3) 当以O、B、P为顶点的三角形的面积为10时,求点P的移动时间.
第10题
第2课时 矩形的判定
1. (2024·泸州)已知四边形ABCD是平行四边形,则添加下列一个条件后,不能判定 ABCD为矩形的是 ( )
A. ∠A=90° B. ∠B=∠C C. AC=BD D. AC⊥BD
2. 下列说法正确的是 ( )
A. 有两个角是直角的四边形是矩形 B. 有三个直角的四边形是矩形
C. 对角线相等的四边形是矩形 D. 对角线互相平分的平行四边形是矩形
3. 如图,在 ABCD中,对角线BD=8cm,AE⊥BD,垂足为E,且AE=3cm,BC=4cm,则AD与BC之间的距离为 cm.
4. 如图,工人师傅砌墙时,要想检验门框ABCD是否符合设计要求(即门框是否为矩形),在确保两组对边分别平行的前提下,只要测量出对角线AC、BD的长度,然后看它们是否相等就可以判断了.
(1) 当AC BD时,门框符合要求(填“=”或“≠”);
(2) 这种做法的依据是 .
5. (2023·贵州)如图,在Rt△ABC中,∠ACB=90°,延长CB至点D,使得BD=CB,过点A、D分别作AE∥BD,DE∥BA,AE与DE相交于点E,连接BE、CE.求证:BE⊥CD,CE=DE.
第5题
第6题
6. 如图,在 ABCD中,对角线AC、BD相交于点O,M、N是BD上两点,BM=DN,连接AM、MC、CN、NA,添加一个条件,使四边形AMCN是矩形,这个条件可以是 ( )
A. OM=AC B. MB=MO
C. BD⊥AC D. ∠AMB=∠CND
第8题
7. 设AB、CD、EF是同一平面内三条互相平行的直线.已知AB与CD之间的距离是12cm,EF与CD之间的距离是5cm,则AB与EF之间的距离是 .
8. 如图,在矩形ABCD中,AB=6,AD=8,且有一点P从点B出发,沿着BD往点D移动,过点P作AB的垂线,交AB于点E,过点P作AD的垂线,交AD于点F,连接EF,则EF长的最小值为 .
9. (2024·贵州)如图,四边形ABCD的对角线AC与BD相交于点O,AD∥BC,∠ABC=90°, .有以下条件:① AB∥CD;② AD=BC.
(1) 请从①②中任选1个填到横线上(填序号),求证:四边形ABCD是矩形;
(2) 在(1)的条件下,若AB=3,AC=5,求四边形ABCD的面积.
第9题
10. 如图,AC=AB,AD=AE,DE=BC,∠BAD=∠CAE.求证:四边形BCDE是矩形(用两种不同的矩形判定方法证明).
第10题
第3课时 菱形的概念与性质
1.
如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论错误的是 ( )
A. AB=AD B. AC⊥BD C. AC=BD D. ∠DAC=∠BAC
2. (2023·湘潭)如图,在菱形ABCD中,连接AC、BD.若∠1=20°,则∠2的度数为 ( )
A. 20° B. 60° C. 70° D. 80°
3. 如图,菱形ABCD的对角线AC、BD交于点O,E为AD的中点,连接OE.若OE=3,则菱形ABCD的周长为 .
4. 如图,在菱形ABCD中,对角线AC、BD交于点O,过点A作AH⊥BC于点H.已知BO=8,S菱形ABCD=96,则AH的长为 .
5. 如图,四边形ABCD为菱形,E为对角线AC上的一个动点(不与点A、C重合),连接DE并延长,交射线AB于点F,连接BE.求证:
(1) △DCE≌△BCE;
(2) ∠AFD=∠EBC.
第5题
第6题
6. 如图,在菱形ABCD中,连接AC、BD,AB=5,AC=6,过点D作DE⊥AB,交BA的延长线于点E,则线段DE的长为 ( )
A. B.
C. 4 D.
7. 如图,菱形ABCD的对角线AC、BD相交于点O,AC=4,BD=16,将△ABO沿AC方向平移,得到△A'B'O'.当点A'与点C重合时,点A与点B'之间的距离为 ( )
A. 6 B. 8 C. 10 D. 12
8. 如图,若菱形ABCD的顶点A、B的坐标分别为(3,0)、(-2,0),点D在y轴正半轴上,则点C的坐标是 .
9. 如图,在菱形ABCD中,AC交BD于点O,DE⊥BC于点E,连接OE.若∠ABC=140°,则∠OED的度数为 .
10. (2023·凉山)如图,在 ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB,交AC于点E.
(1) 求证:AC⊥BD;
(2) 若AB=10,AC=16,求OE的长.
第10题
11. 如图,在菱形ABCD中,对角线AC、BD交于点O,过点D作对角线BD的垂线,交BA的延长线于点E.
(1) 求证:四边形ACDE是平行四边形;
(2) 若AC=16,BD=12,求△ADE的周长.
第11题
第4课时 菱形的判定
1. (2024·通辽)如图, ABCD的对角线AC、BD相交于点O.添加下列一个条件后,不能证明 ABCD是菱形的为 ( )
A. ∠BAC=∠BCA B. ∠ABD=∠CBD C. OA2+OB2=AD2 D. AD2+OA2=OD2
2. 下列说法中,不正确的是 ( )
A. 四边相等的四边形是菱形 B. 对角线垂直的平行四边形是菱形
C. 菱形的对角线互相垂直且相等 D. 菱形的邻边相等
3. (2023·深圳)如图,在 ABCD中,AB=4,BC=6,将线段AB水平向右平移a个单位长度得到线段EF,当a的值为 时,四边形ECDF为菱形.
4. 把一张矩形纸片按如图所示的方法对折两次,然后剪下三角形纸片并展开,得到的图形一定是 (填写一个特殊的平行四边形).
5. (2023·张家界)如图,点A、D、C、B在同一条直线上,且AD=BC,AE=BF,CE=DF,连接DE、CF.
(1) 求证:AE∥BF;
(2) 若DF=FC,求证:四边形DECF是菱形.
第5题
6. 一个平行四边形的一条边的长为,两条对角线长分别为4和2,这个平行四边形是 ( )
A. 矩形 B. 菱形
C. 一般平行四边形 D. 有一个内角是60°的平行四边形
7. (2024·上海)已知四边形ABCD为矩形,过点A、C作对角线BD的垂线,过点B、D作对角线AC的垂线.如果四条垂线段首尾相连拼成一个四边形,那么这个四边形为 ( )
A. 菱形 B. 矩形 C. 直角梯形 D. 等腰梯形
第8题
8. (2023·聊城)如图,在 ABCD中,BC的垂直平分线EO交AD于点E,交BC于点O,连接BE、CE,过点C作CF∥BE,交EO的延长线于点F,连接BF.若AD=8,CE=5,则四边形BFCE的面积为 .
9. 四边形的四条边长分别为a、b、c、d,且满足条件a2+b2+c2+d2=ab+bc+cd+da,则此四边形一定是 .
10. 如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线分别交AD、BC、BD于点M、N、O,连接BM、DN.
(1) 求证:四边形BNDM是菱形;
(2) 若BD=24,MN=10,求菱形BNDM的周长.
第10题
11. 将两张长为8、宽为4的矩形纸片按如图所示的方式叠放.
(1) 判断四边形AGCH的形状,并说明理由;
(2) 求四边形AGCH的面积.
第11题
第5课时 正方形的概念、性质与判定
1.
如图,一个四边形顺次添加下列条件中的三个条件便得到正方形:a. 两组对边分别相等;b. 一组对边平行且相等;c. 一组邻边相等;d. 一个角是直角.顺次添加的条件:① a→c→d;② b→d→c;③ a→b→c.其中,正确的是 ( )
A. 仅① B. 仅③ C. ①② D. ②③
2. 如图,在正方形ABCD中,AB=6,G是BC的中点.将△ABG沿直线AG折叠得到△AFG,延长GF,交DC于点E,则DE的长是 ( )
A. 1 B. 1.5 C. 2 D. 2.5
3. (2024·兴安盟改编)如图,正方形ABCD的对角线AC与BD相交于点O,E是边BC上一点,F是BD上一点,连接DE、EF.若△DEF与△DEC关于直线DE对称,则∠FEB= .
4. 如图,正方形ABCD的对角线AC、BD交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F.若BD=4,则AF的长为 .
5. (2023·绍兴)如图,在正方形ABCD中,G是对角线BD上的一点(不与点B、D重合),GE⊥CD,GF⊥BC,垂足分别为E、F.连接EF、AG,延长AG交EF于点H.
(1) 求证:∠DAG=∠EGH;
(2) 判断AH与EF是否垂直,并说明理由.
第5题
第6题
6. (2023·重庆A卷)如图,在正方形ABCD中,点E、F分别在BC、CD上,连接AE、AF、EF,∠EAF=45°.若∠BAE=α,则∠FEC一定等于 ( )
A. 2α
B. 90°-2α
C. 45°-α
D. 90°-α
7. (2024·重庆A卷改编)如图,正方形ABCD的边CD上有一点E,连接AE,将AE绕点E按逆时针方向旋转90°,得到FE,连接CF并延长,与AB的延长线交于点G,则∠G的度数为( )
A. 40° B. 45° C. 50° D. 60°
8. (2023·重庆B卷改编)如图,在正方形ABCD中,O为对角线AC的中点,E为正方形内一点,连接BE,BE=BA,连接CE并延长,与∠ABE的平分线交于点F,连接OF.若AB=1,则OF的长为 .
9. 如图,过直线AP上一点A作正方形ABCD,∠PAD=30°,若以点B为圆心,AB的长为半径作弧,与AP交于点A、M,分别以点A、M为圆心,AM的长为半径作弧,两弧交于点E,连接ED,则∠ADE的度数为 .
10. 如图,在正方形ABCD中,E、F、G、H分别是各边上的点,且AE=BF=CG=DH.求证:
(1) △AHE≌△BEF;
(2) 四边形EFGH是正方形.
第10题
11. 如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
(1) 求证:BQ=AP;
(2) 在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段的长度差等于PQ的长.
第11题
9.4 矩形、菱形、正方形
第1课时 矩形的概念与性质
1. C 2. D 3. 57° 4. 4
5. (1) ∵ 四边形ABCD是矩形,∴ AB∥CD,即FA∥CD.∴ ∠FAE=∠CDE.∵ E是AD的中点,∴ AE=DE.又∵ ∠FEA=∠CED,∴ △FAE≌△CDE.∴ FA=CD.∴ 四边形ACDF是平行四边形 (2) BC=2CD 理由:∵ 四边形ABCD是矩形,∴ AD=BC,∠ADC=∠BCD=90°.∵ CF平分∠BCD,∴ ∠DCE=45°.∴ 在Rt△CDE中,∠DCE=∠DEC=45°.∴ CD=DE.∵ E是AD的中点,∴ AD=2DE=2CD.∴ BC=2CD.
6. C 7. 46°或106°
8. 解析:连接EG.设CG=x.根据作图过程,可知BC=BE=10,BF是∠EBC的平分线,证△EBG≌△CBG,得EG=CG=x.先在Rt△BAE中,利用勾股定理求得AE=8,从而可得DE=2,再在Rt△EDG中,利用勾股定理,构造方程22+(6-x)2=x2,由此可求出CG的长.
9. (1) ∵ 四边形ABCD是矩形,∴ AB=CD,AB∥CD.∴ ∠ABE=∠CDF.∵ AE⊥BD,CF⊥BD,∴ ∠AEB=∠CFD=90°.在△ABE和△CDF中,∴ △ABE≌△CDF.∴ AE=CF (2) △ABE、△CDF、△BCE、△ADF
10. (1) (4,6) (1,6) (2) 由题意,可得OA=BC=4,OC=AB=6.当点P到x轴的距离为4个单位长度时,分两种情况讨论:① 当点P在OC上时,OP=4.∴ 点P的移动时间为4÷2=2(秒).② 当点P在AB上时,AP=4.∴ 点P的移动时间为(6+4+6-4)÷2=6(秒).综上所述,点P的移动时间为2秒或6秒 (3) ① 当点P在OC上时,如图①.由题意,得BC·OP=10,即×4OP=10.∴ OP=5.∴ 点P的移动时间为5÷2=(秒).② 当点P在BC上时,如图②.由题意,得OC·PB=10,即×6PB=10.∴ BP=.∴ CP=.∴ 点P的移动时间为6+÷2=(秒).③ 当点P在AB上时,如图③.由题意,得BP·BC=10,即BP×4=10.∴ BP=5.∴ 点P的移动时间为(6+4+5)÷2=(秒).④ 当点P在OA上时,如图④.由题意,得OP·AB=10,即OP×6=10.∴ OP=.∴ 点P的移动时间为6+4+6+4-÷2=(秒).综上所述,点P的移动时间为秒或秒或秒或秒
第2课时 矩形的判定
1. D 2. B 3. 6 4. (1) = (2) 对角线相等的平行四边形是矩形
5. ∵ AE∥BD,DE∥BA,∴ 四边形ABDE是平行四边形.∴ AE=BD,AB=DE.∵ BD=BC,∴ AE=BC.∵ AE∥BD,即AE∥BC,∴ 四边形AEBC是平行四边形.∵ ∠ACB=90°,∴ 四边形AEBC是矩形.∴ ∠EBC=90°,AB=CE.∴ BE⊥CD,CE=DE
6. A 7. 7cm或17cm
8. 解析:根据题意,得四边形AEPF为矩形,连接AP,则AP=EF,将求EF长的最小值转化成求AP长的最小值.由于垂线段最短,因此当AP⊥BD时,AP的长取得最小值.此时 S△ABD=AB·AD=BD·AP,得AP=,∴ EF长的最小值为.
9. (1) 选择不唯一,如选择① ∵ AD∥BC,AB∥CD,∴ 四边形ABCD是平行四边形.∵ ∠ABC=90°,∴ 四边形ABCD是矩形 (2) ∵ ∠ABC=90°,AB=3,AC=5,∴ BC==4.∵ 四边形ABCD是矩形,∴ 四边形ABCD的面积=AB·BC=3×4=12
10. 证法一:∵ ∠BAD=∠CAE,∴ ∠BAD-∠BAC=∠CAE-∠BAC,即∠CAD=∠BAE.又∵ AC=AB,AD=AE,∴ △CAD≌△BAE.∴ ∠CDA=∠BEA,CD=BE.又∵ DE=BC,∴ 四边形BCDE是平行四边形.∴ BE∥CD.∴ ∠CDE+∠BED=180°.∵ AD=AE,∴ ∠ADE=∠AED.∴ ∠CDA-∠ADE=∠BEA-∠AED,即∠CDE=∠BED.∴ ∠CDE=∠BED=90°.∴ 四边形BCDE是矩形 证法二:同证法一,得△CAD≌△BAE,∴ CD=BE.又∵ DE=BC,∴ 四边形BCDE是平行四边形.连接BD、CE.∵ AB=AC,∠BAD=∠CAE,AD=AE,∴ △BAD≌△CAE.∴ BD=CE.∴ 四边形BCDE是矩形
第3课时 菱形的概念与性质
1. C 2. C 3. 24 4.
5. (1) ∵ 四边形ABCD是菱形,∴ CD=CB,∠DCE=∠BCE.在△DCE和△BCE中,∴ △DCE≌△BCE (2) ∵ 四边形ABCD是菱形,∴ DC∥AF.∴ ∠CDF=∠AFD.∵ △DCE≌△BCE,∴ ∠CDF=∠EBC.∴ ∠AFD=∠EBC
6. D 7. C 8. (-5,4) 9. 20°
10. (1) ∵ ∠CAB=∠ACB,∴ AB=CB.∵ 四边形ABCD是平行四边形,∴ ABCD是菱形.∴ AC⊥BD (2) 设OE=x.∵ ABCD是菱形,AC=16,∴ OA=AC=8.∵ AC⊥BD,∴ ∠AOB=∠BOE=90°.∴ 在Rt△AOB中,OB===6.∴ 在Rt△EOB中,BE2=OE2+OB2=x2+62.∵ BE⊥AB,∴ ∠EBA=90°.∴ 在Rt△ABE中,BE2=AE2-AB2=(8+x)2-102.∴ x2+62=(8+x)2-102,解得x=.∴ OE的长为
11. (1) ∵ 四边形ABCD是菱形,∴ AB∥CD,AC⊥BD.∴ AE∥CD.又∵ DE⊥BD,∴ DE∥AC.∴ 四边形ACDE是平行四边形 (2) ∵ 四边形ABCD是菱形,AC=16,BD=12,∴ AC⊥BD,AD=CD,AO=AC=8,DO=BD=6.∴ 在Rt△AOD中,AD==10.∴ CD=10.∵ 四边形ACDE是平行四边形,∴ AE=CD=10,DE=AC=16.∴ △ADE的周长为AD+AE+DE=36
第4课时 菱形的判定
1. D 2. C 3. 2 4. 菱形
5. (1) ∵ AD=BC,∴ AD+CD=BC+CD,即AC=BD.在△AEC和△BFD中,∴ △AEC≌△BFD.∴ ∠A=∠B.∴ AE∥BF (2) ∵ △AEC≌△BFD,∴ ∠ECA=∠FDB.∴ EC∥DF.∵ EC=DF,∴ 四边形DECF是平行四边形.∵ DF=FC,∴ 四边形DECF是菱形
6. B 7. A
8. 24 解析:由平行四边形的性质,得BC=AD=8.∵ EF垂直平分BC,∴ EF⊥BC,OC=OB=BC=4.∴ 在Rt△EOC中,由勾股定理,得OE=3.证△OCF≌△OBE,得OE=OF=3,由此可说明四边形BFCE为菱形,∴ S四边形BFCE=BC·EF=24.
9. 菱形
10. (1) ∵ AD∥BC,∴ ∠DMO=∠BNO.∵ MN是对角线BD的垂直平分线,∴ OD=OB,MN⊥BD.在△MOD和△NOB中,∴ △MOD≌△NOB.∴ OM=ON.∵ OD=OB,∴ 四边形BNDM是平行四边形.∵ MN⊥BD,∴ 四边形BNDM是菱形 (2) ∵ 四边形BNDM是菱形,BD=24,MN=10,∴ BM=BN=DM=DN,OB=BD=12,OM=MN=5.∵ MN⊥BD,∴ ∠BOM=90°.在Rt△BOM中,由勾股定理,得BM===13.∴ 菱形BNDM的周长=4BM=4×13=52
11. (1) 四边形AGCH是菱形 理由:∵ 四边形ABCD和四边形AFCE是矩形,∴ ∠B=∠F=90°,AD∥BC,AF∥CE.∴ 四边形AGCH是平行四边形.∵ S AGCH=GC·AB=AG·CF,AB=CF=4,∴ GC=AG.∴ 四边形AGCH是菱形. (2) 由(1)可知,GC=AG.设GC=AG=x,则BG=8-x.∵ 在矩形ABCD中,∠B=90°,AB=4,∴ 在Rt△ABG中,由勾股定理,得42+(8-x)2=x2,解得x=5.∴ GC=5.∴ S菱形AGCH=GC·AB=5×4=20
第5课时 正方形的概念、性质与判定
1. C 2. C 3. 45° 4.
5. (1) ∵ 四边形ABCD是正方形,∴ ∠ADC=90°.∵ GE⊥CD,∴ ∠GEC=90°.∴ ∠ADC=∠GEC.∴ AD∥GE.∴ ∠DAG=∠EGH (2) AH⊥EF 理由:如图,连接GC,交EF于点O. ∵ 在正方形ABCD中,BD是对角线,∴ ∠BCD=90°,∠ADG=∠CDG,AD=CD.∵ DG=DG,∴ △ADG≌△CDG.∴ ∠DAG=∠DCG.∵ GE⊥CD,GF⊥BC,∴ ∠GFC=∠GEC=90°=∠BCD.∴ 四边形FCEG为矩形.∴ GC=EF,OE=EF,OC=GC.∴ OE=OC.∴ ∠OEC=∠OCE.∴ ∠DAG=∠OEC.由(1),得∠DAG=∠EGH,∴ ∠EGH=∠OEC.∵ ∠GEC=∠OEC+∠GEH=90°,∴ ∠EGH+∠GEH=90°.∴ ∠GHE=90°.∴ AH⊥EF.
6. A 解析:延长FD至点G,使得DG=BE,连接AG,可证△ADG≌△ABE.∴ ∠G=∠AEB=90°-α,AG=AE,∠GAD=∠EAB.∴ 易得∠GAF=∠EAF=45°.又∵ AF=AF,∴ △GAF≌△EAF.∴ ∠AEF=∠G=90°-α.∴ ∠FEC=180°-∠AEB-∠AEF=2α.
7. B 8. 9. 15°或45°
10. (1) ∵ 四边形ABCD为正方形,∴ AB=BC=CD=AD,∠A=∠B=∠C=∠D=90°.∵ AE=BF=CG=DH,∴ BE=CF=DG=AH.∴ △AHE≌△BEF (2) ∵ AE=BF=CG=DH,AH=BE=CF=DG,∠A=∠B=∠C=∠D=90°,∴ △AEH≌△BFE≌△CGF≌△DHG.∴ EH=FE=GF=HG,∠EHA=∠HGD.∴ 四边形EFGH是菱形.∵ ∠D=90°,∴ ∠HGD+∠GHD=90°.∴ ∠EHA+∠GHD=90°.∴ ∠EHG=90°.∴ 四边形EFGH是正方形
11. (1) ∵ 四边形ABCD是正方形,∴ BA=DA,∠BAD=90°,即∠BAQ+∠DAP=90°.∵ DP⊥AQ,∴ ∠ADP+∠DAP=90°.∴ ∠BAQ=∠ADP.∵ AQ⊥BE,DP⊥AQ,∴ ∠AQB=∠DPA=90°.∴ △AQB≌△DPA.∴ BQ=AP (2) AQ-AP=PQ,AQ-BQ=PQ,DP-AP=PQ,DP-BQ=PQ
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
