11.3 用反比例函数解决问题(含答案) 2024-2025学年数学苏科版八年级下册
文档属性
| 名称 | 11.3 用反比例函数解决问题(含答案) 2024-2025学年数学苏科版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 85.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-03 20:10:09 | ||
图片预览

文档简介
11.3 用反比例函数解决问题
1. (2023·怀化)已知压力F(N)、压强p(Pa)与受力面积S(m2)之间有如下关系式:F=pS.当F为定值时,能大致表示p与S之间函数关系的图像是 ( )
2. 为了建设生态文明,某工厂自去年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的关系如图所示,治污完成前是反比例函数图像的一部分,治污完成后是一次函数图像的一部分,下列结论错误的是 ( )
第2题
A. 4月的利润为50万元
B. 治污改造完成后每月利润比前一个月增加30万元
C. 治污改造完成前后共有4个月的利润低于100万元
D. 9月该工厂的利润达到200万元
3. 把一块棱长为40cm的正方体钢锭锻造成横截面面积为Scm2、长为hcm的钢筋,则S关于h的函数表达式为 .
4. (2023·扬州)某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数,且当V=3时,p=8000.当气球内的气体压强大于40000Pa时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于 m3.
5. 张叔叔驾驶小汽车匀速地从A地行驶到B地,行驶路程为480km.设小汽车的行驶时间为th,行驶速度为vkm/h,且全程速度限定为不超过120km/h.
(1) v关于t的函数表达式为 (写出自变量t的取值范围).
(2) 张叔叔8:00驾驶小汽车从A地出发.
① 若张叔叔需在当天12:48至14:00间(含12:48和14:00)到达B地,求v的取值范围;
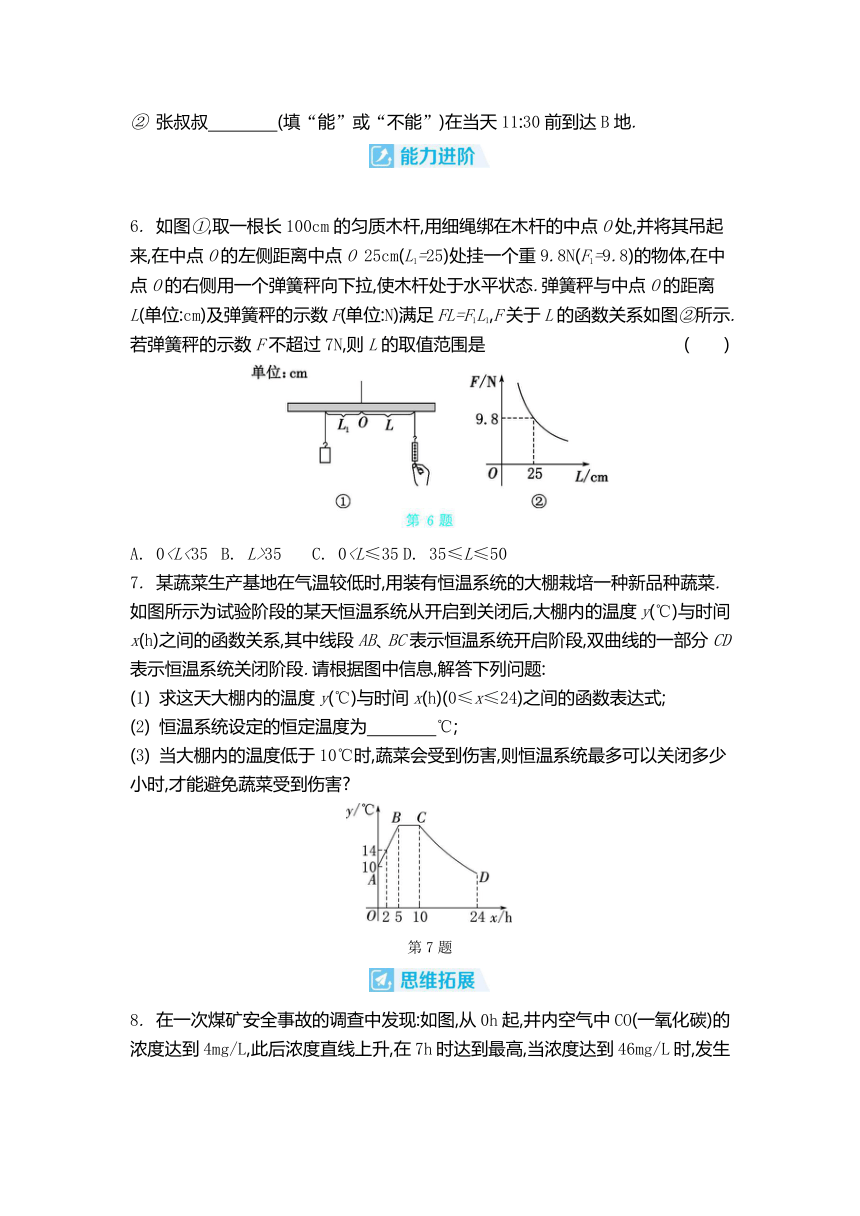
② 张叔叔 (填“能”或“不能”)在当天11:30前到达B地.
6. 如图①,取一根长100cm的匀质木杆,用细绳绑在木杆的中点O处,并将其吊起来,在中点O的左侧距离中点O 25cm(L1=25)处挂一个重9.8N(F1=9.8)的物体,在中点O的右侧用一个弹簧秤向下拉,使木杆处于水平状态.弹簧秤与中点O的距离L(单位:cm)及弹簧秤的示数F(单位:N)满足FL=F1L1,F关于L的函数关系如图②所示.若弹簧秤的示数F不超过7N,则L的取值范围是 ( )
A. 035 C. 07. 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图所示为试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y(℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.请根据图中信息,解答下列问题:
(1) 求这天大棚内的温度y(℃)与时间x(h)(0≤x≤24)之间的函数表达式;
(2) 恒温系统设定的恒定温度为 ℃;
(3) 当大棚内的温度低于10℃时,蔬菜会受到伤害,则恒温系统最多可以关闭多少小时,才能避免蔬菜受到伤害
第7题
8. 在一次煤矿安全事故的调查中发现:如图,从0h起,井内空气中CO(一氧化碳)的浓度达到4mg/L,此后浓度直线上升,在7h时达到最高,当浓度达到46mg/L时,发生爆炸,爆炸后空气中CO的浓度下降,此时浓度与时间成反比例.根据题中相关信息,回答下列问题:
(1) 求爆炸前、后空气中CO的浓度y(mg/L)与时间x(h)之间的函数表达式,并写出相应的自变量x的取值范围.
(2) 当空气中的CO浓度达到34mg/L时,井下3km处的矿工接到自动报警信号,这时他们至少要以多少的速度撤离才能在爆炸前逃生
(3) 矿工只有在空气中CO的浓度降到4mg/L及以下时,才能回到矿井开展生产救援工作,则矿工至少在爆炸后多长时间才能下井
第8题
11.3 用反比例函数解决问题
1. D 2. C 3. S= 4. 0.6
5. (1) v=(t≥4) (2) ① ∵ 8:00至12:48的时长为4.8h,8:00至14:00的时长为6h,∴ 4.8≤t≤6.将t=6代入v=,得v=80;将t=4.8代入v=,得v=100.∴ v的取值范围是80≤v≤100
② 不能 解析:∵ 8:00至11:30的时长为3.5h,∴ 若张叔叔要在当天11:30前到达B地,则必须满足t<3.5,此时v>120,即超过限定速度.∴ 张叔叔不能在当天11:30前到达B地.
6. D
7. (1) 设AB所在直线对应的函数表达式为y=k1x+b(k1≠0).∵ AB过点(0,10)、(2,14),∴ 解得∴ AB所在直线对应的函数表达式为y=2x+10.∵ 点B在AB上,当x=5时,y=2×5+10=20,∴ 点B的坐标为(5,20).∴ BC所在直线对应的函数表达式为y=20.∴ 点C的坐标为(10,20).设CD所在双曲线对应的函数表达式为y=(k2≠0).将(10,20)代入,得k2=200.∴ CD所在双曲线对应的函数表达式为y=.综上所述,这天大棚内的温度y(℃)与时间x(h)(0≤x≤24)之间的函数表达式为y= (2) 20 (3) 在y=中,令y=10,得x=20,此时20-10=10(h).∴ 恒温系统最多可以关闭10h,才能避免蔬菜受到伤害
8. (1) 设爆炸前空气中CO的浓度y(mg/L)与时间x(h)之间的函数表达式为y=k1x+b(k1≠0).由题图,可知直线y=k1x+b过点(0,4)、(7,46),∴ 解得∴ y=6x+4.此时自变量x的取值范围是0≤x≤7.∵ 爆炸后空气中CO的浓度下降,且浓度与时间成反比例,∴ 可设y与x之间的函数表达式为y=(k2≠0).由题图,可知函数y=的图像过点(7,46),∴ =46,解得k2=322.∴ y=.此时自变量x的取值范围是x>7 (2) 在y=6x+4中,令y=34,得6x+4=34,解得x=5.∴ 撤离的最长时间为7-5=2(h).∴ 撤离的最慢速度为3÷2=1.5(km/h),即他们至少要以1.5km/h的速度撤离才能在爆炸前逃生 (3) 在y=中,令y≤4,解得x≥80.5.∵ 80.5-7=73.5(h),∴ 矿工至少在爆炸后73.5h才能下井
1. (2023·怀化)已知压力F(N)、压强p(Pa)与受力面积S(m2)之间有如下关系式:F=pS.当F为定值时,能大致表示p与S之间函数关系的图像是 ( )
2. 为了建设生态文明,某工厂自去年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的关系如图所示,治污完成前是反比例函数图像的一部分,治污完成后是一次函数图像的一部分,下列结论错误的是 ( )
第2题
A. 4月的利润为50万元
B. 治污改造完成后每月利润比前一个月增加30万元
C. 治污改造完成前后共有4个月的利润低于100万元
D. 9月该工厂的利润达到200万元
3. 把一块棱长为40cm的正方体钢锭锻造成横截面面积为Scm2、长为hcm的钢筋,则S关于h的函数表达式为 .
4. (2023·扬州)某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数,且当V=3时,p=8000.当气球内的气体压强大于40000Pa时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于 m3.
5. 张叔叔驾驶小汽车匀速地从A地行驶到B地,行驶路程为480km.设小汽车的行驶时间为th,行驶速度为vkm/h,且全程速度限定为不超过120km/h.
(1) v关于t的函数表达式为 (写出自变量t的取值范围).
(2) 张叔叔8:00驾驶小汽车从A地出发.
① 若张叔叔需在当天12:48至14:00间(含12:48和14:00)到达B地,求v的取值范围;
② 张叔叔 (填“能”或“不能”)在当天11:30前到达B地.
6. 如图①,取一根长100cm的匀质木杆,用细绳绑在木杆的中点O处,并将其吊起来,在中点O的左侧距离中点O 25cm(L1=25)处挂一个重9.8N(F1=9.8)的物体,在中点O的右侧用一个弹簧秤向下拉,使木杆处于水平状态.弹簧秤与中点O的距离L(单位:cm)及弹簧秤的示数F(单位:N)满足FL=F1L1,F关于L的函数关系如图②所示.若弹簧秤的示数F不超过7N,则L的取值范围是 ( )
A. 0
(1) 求这天大棚内的温度y(℃)与时间x(h)(0≤x≤24)之间的函数表达式;
(2) 恒温系统设定的恒定温度为 ℃;
(3) 当大棚内的温度低于10℃时,蔬菜会受到伤害,则恒温系统最多可以关闭多少小时,才能避免蔬菜受到伤害
第7题
8. 在一次煤矿安全事故的调查中发现:如图,从0h起,井内空气中CO(一氧化碳)的浓度达到4mg/L,此后浓度直线上升,在7h时达到最高,当浓度达到46mg/L时,发生爆炸,爆炸后空气中CO的浓度下降,此时浓度与时间成反比例.根据题中相关信息,回答下列问题:
(1) 求爆炸前、后空气中CO的浓度y(mg/L)与时间x(h)之间的函数表达式,并写出相应的自变量x的取值范围.
(2) 当空气中的CO浓度达到34mg/L时,井下3km处的矿工接到自动报警信号,这时他们至少要以多少的速度撤离才能在爆炸前逃生
(3) 矿工只有在空气中CO的浓度降到4mg/L及以下时,才能回到矿井开展生产救援工作,则矿工至少在爆炸后多长时间才能下井
第8题
11.3 用反比例函数解决问题
1. D 2. C 3. S= 4. 0.6
5. (1) v=(t≥4) (2) ① ∵ 8:00至12:48的时长为4.8h,8:00至14:00的时长为6h,∴ 4.8≤t≤6.将t=6代入v=,得v=80;将t=4.8代入v=,得v=100.∴ v的取值范围是80≤v≤100
② 不能 解析:∵ 8:00至11:30的时长为3.5h,∴ 若张叔叔要在当天11:30前到达B地,则必须满足t<3.5,此时v>120,即超过限定速度.∴ 张叔叔不能在当天11:30前到达B地.
6. D
7. (1) 设AB所在直线对应的函数表达式为y=k1x+b(k1≠0).∵ AB过点(0,10)、(2,14),∴ 解得∴ AB所在直线对应的函数表达式为y=2x+10.∵ 点B在AB上,当x=5时,y=2×5+10=20,∴ 点B的坐标为(5,20).∴ BC所在直线对应的函数表达式为y=20.∴ 点C的坐标为(10,20).设CD所在双曲线对应的函数表达式为y=(k2≠0).将(10,20)代入,得k2=200.∴ CD所在双曲线对应的函数表达式为y=.综上所述,这天大棚内的温度y(℃)与时间x(h)(0≤x≤24)之间的函数表达式为y= (2) 20 (3) 在y=中,令y=10,得x=20,此时20-10=10(h).∴ 恒温系统最多可以关闭10h,才能避免蔬菜受到伤害
8. (1) 设爆炸前空气中CO的浓度y(mg/L)与时间x(h)之间的函数表达式为y=k1x+b(k1≠0).由题图,可知直线y=k1x+b过点(0,4)、(7,46),∴ 解得∴ y=6x+4.此时自变量x的取值范围是0≤x≤7.∵ 爆炸后空气中CO的浓度下降,且浓度与时间成反比例,∴ 可设y与x之间的函数表达式为y=(k2≠0).由题图,可知函数y=的图像过点(7,46),∴ =46,解得k2=322.∴ y=.此时自变量x的取值范围是x>7 (2) 在y=6x+4中,令y=34,得6x+4=34,解得x=5.∴ 撤离的最长时间为7-5=2(h).∴ 撤离的最慢速度为3÷2=1.5(km/h),即他们至少要以1.5km/h的速度撤离才能在爆炸前逃生 (3) 在y=中,令y≤4,解得x≥80.5.∵ 80.5-7=73.5(h),∴ 矿工至少在爆炸后73.5h才能下井
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
