第9章 中心对称图形——平行四边形 同步练(含答案) 2024-2025学年数学苏科版八年级下册
文档属性
| 名称 | 第9章 中心对称图形——平行四边形 同步练(含答案) 2024-2025学年数学苏科版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 367.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-03 20:12:38 | ||
图片预览

文档简介
第9章 中心对称图形——平行四边形
整合提升
考点一 图形旋转的性质与中心对称图形
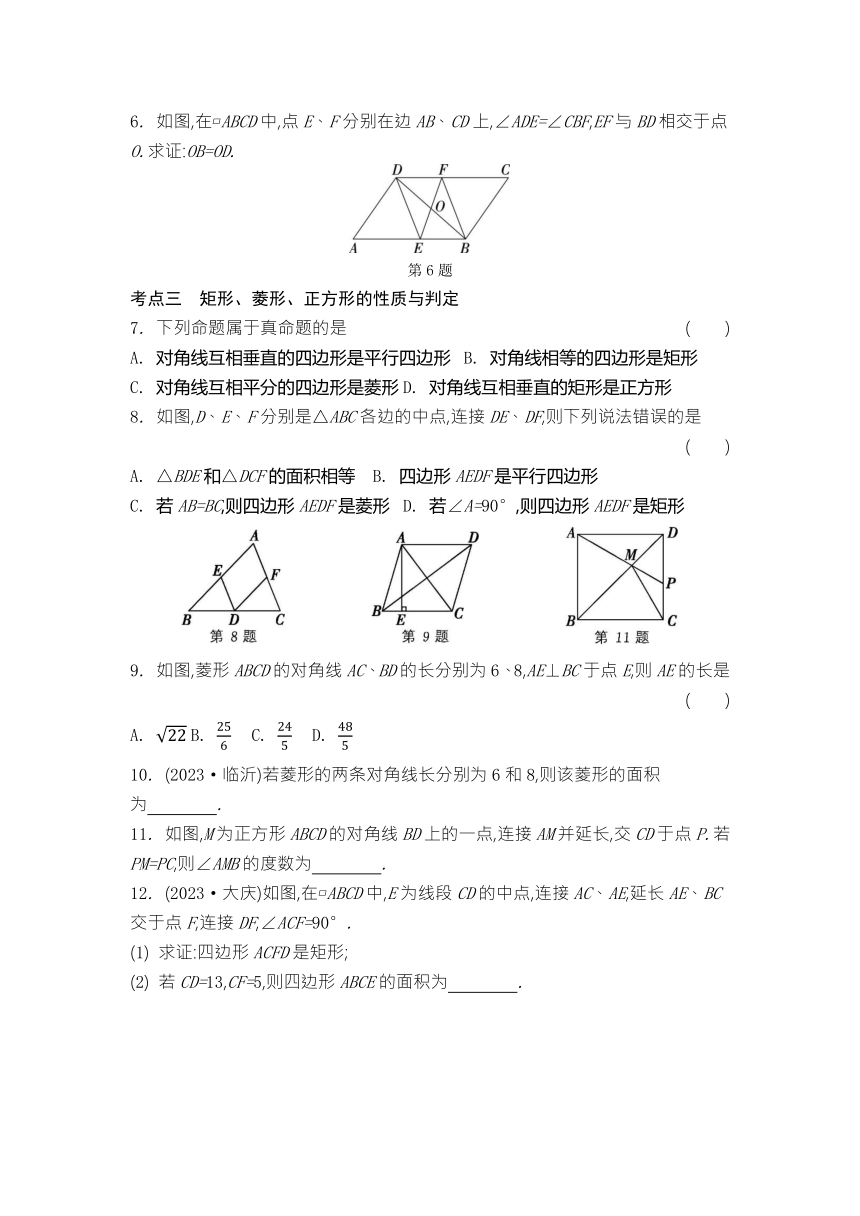
1. (2024·长沙)下列图形中,既是轴对称图形,又是中心对称图形的为 ( )
第2题
2. 如图,在正方形网格中,△EFG绕某一点旋转某一角度得到△RPQ,则旋转中心可能是 ( )
A. 点A B. 点B
C. 点C D. 点D
考点二 平行四边形的性质与判定
3. 小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了其中两块碎玻璃,其编号应该是 ( )
A. ①③ B. ①② C. ③④ D. ②④
4. 如图,在 ABCD中,EF∥AD,HN∥AB,则图中的平行四边形共有 ( )
A. 12个 B. 9个 C. 7个 D. 5个
5. 如图,在 ABCD中,点E在AD上,且EC平分∠BED.若∠EBC=30°,BE=10,则 ABCD的面积为 .
6. 如图,在 ABCD中,点E、F分别在边AB、CD上,∠ADE=∠CBF,EF与BD相交于点O.求证:OB=OD.
第6题
考点三 矩形、菱形、正方形的性质与判定
7. 下列命题属于真命题的是 ( )
A. 对角线互相垂直的四边形是平行四边形 B. 对角线相等的四边形是矩形
C. 对角线互相平分的四边形是菱形 D. 对角线互相垂直的矩形是正方形
8. 如图,D、E、F分别是△ABC各边的中点,连接DE、DF,则下列说法错误的是 ( )
A. △BDE和△DCF的面积相等 B. 四边形AEDF是平行四边形
C. 若AB=BC,则四边形AEDF是菱形 D. 若∠A=90°,则四边形AEDF是矩形
9. 如图,菱形ABCD的对角线AC、BD的长分别为6、8,AE⊥BC于点E,则AE的长是 ( )
A. B. C. D.
10. (2023·临沂)若菱形的两条对角线长分别为6和8,则该菱形的面积为 .
11. 如图,M为正方形ABCD的对角线BD上的一点,连接AM并延长,交CD于点P.若PM=PC,则∠AMB的度数为 .
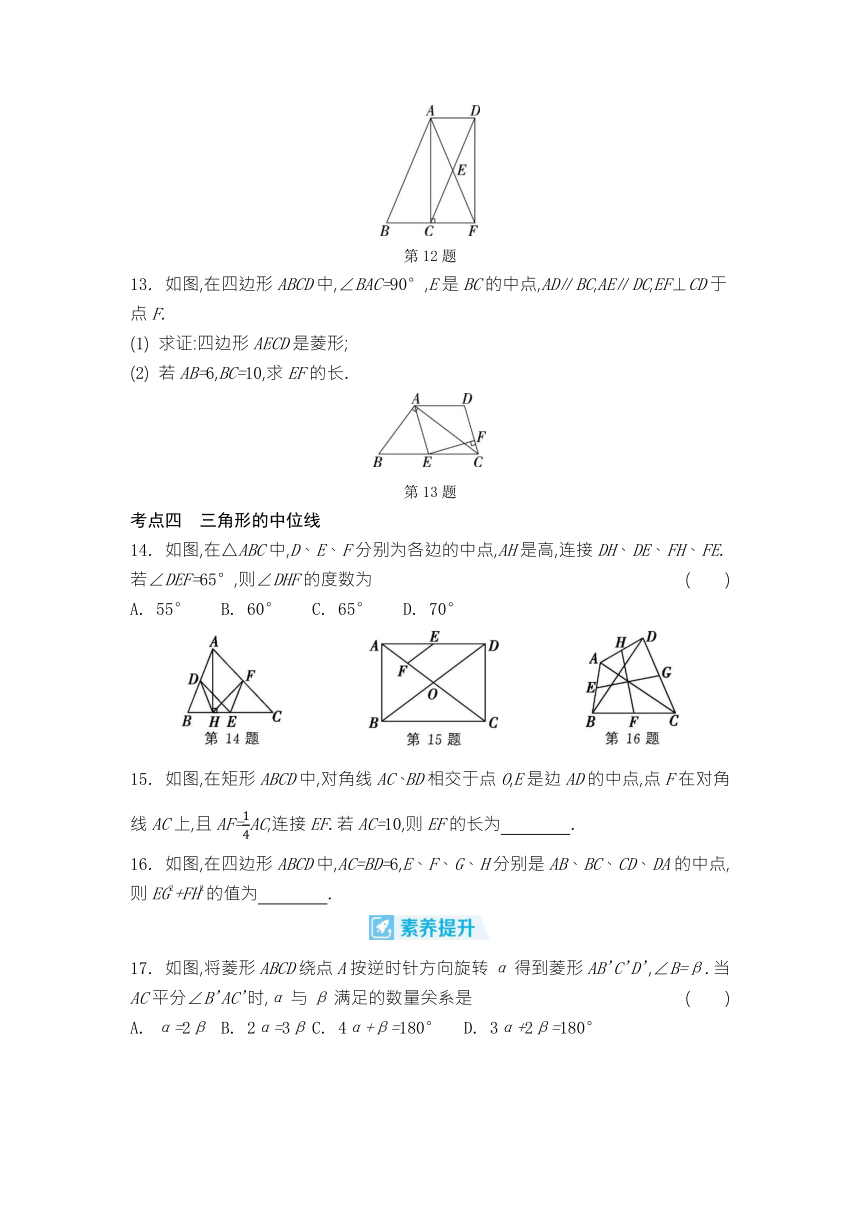
12. (2023·大庆)如图,在 ABCD中,E为线段CD的中点,连接AC、AE,延长AE、BC交于点F,连接DF,∠ACF=90°.
(1) 求证:四边形ACFD是矩形;
(2) 若CD=13,CF=5,则四边形ABCE的面积为 .
第12题
13. 如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.
(1) 求证:四边形AECD是菱形;
(2) 若AB=6,BC=10,求EF的长.
第13题
考点四 三角形的中位线
14. 如图,在△ABC中,D、E、F分别为各边的中点,AH是高,连接DH、DE、FH、FE.若∠DEF=65°,则∠DHF的度数为 ( )
A. 55° B. 60° C. 65° D. 70°
15. 如图,在矩形ABCD中,对角线AC、BD相交于点O,E是边AD的中点,点F在对角线AC上,且AF=AC,连接EF.若AC=10,则EF的长为 .
16. 如图,在四边形ABCD中,AC=BD=6,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2的值为 .
17. 如图,将菱形ABCD绕点A按逆时针方向旋转α得到菱形AB'C'D',∠B=β.当AC平分∠B'AC'时,α与β满足的数量关系是 ( )
A. α=2β B. 2α=3β C. 4α+β=180° D. 3α+2β=180°
18. 如图,在矩形ABCD中,AB=1,BC=2,点A在x轴正半轴上,点D在y轴正半轴上.当点A在x轴上运动时,点D也随之在y轴上运动,在这个运动过程中,点C到原点O的最大距离为 .
19. (2023·哈尔滨)已知四边形ABCD是平行四边形,点E在对角线BD上,点F在边BC上,连接AE、EF,DE=BF,BE=BC.
(1) 如图①,求证:△AED≌△EFB;
(2) 如图②,若AB=AD,AE≠ED,过点C作CH∥AE,交BE于点H,则图②中与∠BAE相等的角是 .
20. 如图,在四边形ABCD中,AB∥CD,AB=AD,CB=CD,E是CD上一点,BE交AC于点F,连接DF.
(1) 求证:四边形ABCD是菱形;
(2) 试确定点E的位置,使得∠BCD=∠EFD,并说明理由.
第20题
21. 已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM、EM.
(1) 如图①,点E在CD上,点G在BC的延长线上,请判断DM、EM的数量关系与位置关系,并直接写出结论.
(2) 如图②,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立 如果成立,请给出证明;如果不成立,请说明理由.
(3) 将图①中的正方形CEFG绕点C旋转,使D、E、F三点在一条直线上.若AB=13,CE=5,请画出图形,并直接写出MF的长.
第9章 中心对称图形——
平行四边形
1. B 2. C 3. A 4. B 5. 50
6. ∵ 四边形ABCD是平行四边形,∴ AB=CD,AD=CB,∠A=∠C.在△DAE和△BCF中,∴ △DAE≌△BCF.∴ DE=BF,AE=CF.∵ AB=CD,∴ AB-AE=CD-CF,即BE=DF.∴ 四边形BFDE是平行四边形.∴ OB=OD
7. D 8. C 9. C 10. 24 11. 75°
12. (1) ∵ 四边形ABCD是平行四边形,∴ AD∥BC.∴ ∠ADE=∠FCE,∠DAE=∠CFE.∵ E为线段CD的中点,∴ DE=CE.∴ △ADE≌△FCE.∴ AE=FE.∴ 四边形ACFD是平行四边形.∵ ∠ACF=90°,∴ 四边形ACFD是矩形 (2) 45
13. (1) ∵ AD∥BC,AE∥DC,∴ 四边形AECD是平行四边形.∵ 在Rt△BAC中,∠BAC=90°,E是BC的中点,∴ AE=BC=CE.∴ 四边形AECD是菱形 (2) 如图,过点A作AH⊥BC于点H.∵ ∠BAC=90°,AB=6,BC=10,∴ AC==8.∵ BC·AH=AB·AC=2S△BAC,∴ AH===.由(1),得四边形AECD是菱形,∴ CE=CD.∵ S菱形AECD=CE·AH=CD·EF,∴ EF=AH=
14. C 解析:利用三角形中位线定理,得DE∥AC,EF∥AB,由此得四边形ADEF是平行四边形,∴ ∠DEF=∠DAF.利用直角三角形斜边上的中线的性质可说明DH=DA,HF=AF,∴ ∠DAH=∠DHA,∠FAH=∠FHA,即∠DAF=∠DHF,从而可得∠DHF=∠DEF=65°.
15. 16. 36 17. C
18. 1+ 解析:取AD的中点H,连接CH、OH.由勾股定理可求CH=,由直角三角形斜边上中线的性质可求OH=AD=1.注意到CO≤OH+CH,由此可知当点O、H、C共线时,CO长取得最大值,最大值为OH+CH=1+.
19. (1) ∵ 四边形ABCD是平行四边形,∴ AD∥BC,AD=BC.∴ ∠ADE=∠EBF.∵ BC=BE,∴ AD=BE.在△AED和△EFB中,∴ △AED≌△EFB (2) ∠AEB、∠DHC、∠EFC、∠DCH
20. (1) 在△ABC和△ADC中,∴ △ABC≌△ADC.∴ ∠BAC=∠DAC.∵ AB∥CD,∴ ∠BAC=∠ACD.∴ ∠DAC=∠ACD.∴ AD=CD.∵ AB=AD,CB=CD,∴ AB=CB=CD=AD.∴ 四边形ABCD是菱形 (2) 当 BE⊥CD时,∠BCD=∠EFD 理由:由(1),得四边形ABCD是菱形,∴ ∠BCF=∠DCF.在△BCF和△DCF中,∴ △BCF≌△DCF.∴ ∠CBF=∠CDF.∵ BE⊥CD,∴ ∠BEC=∠DEF=90°.∴ 易得∠BCD=∠EFD.
21. (1) DM=EM,DM⊥EM (2) (1)中的结论仍然成立,即DM=EM,DM⊥EM 延长EM交DA的延长线于点H.∵ 四边形ABCD与四边形CEFG是正方形,∴ ∠ADE=∠DEF=90°,AD=CD,EC=FE.∴ ∠ADE+∠DEF=180°.∴ AD∥EF.∴ ∠MAH=∠MFE.∵ M是AF的中点,∴ AM=FM.又∵ ∠AMH=∠FME,∴ △AMH≌△FME.∴ MH=ME,AH=FE=EC.∴ DH=DE.∴ 在Rt△EDH中,DM=EM,DM⊥EM (3) 如图①,MF=;如图②,MF=
整合提升
考点一 图形旋转的性质与中心对称图形
1. (2024·长沙)下列图形中,既是轴对称图形,又是中心对称图形的为 ( )
第2题
2. 如图,在正方形网格中,△EFG绕某一点旋转某一角度得到△RPQ,则旋转中心可能是 ( )
A. 点A B. 点B
C. 点C D. 点D
考点二 平行四边形的性质与判定
3. 小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了其中两块碎玻璃,其编号应该是 ( )
A. ①③ B. ①② C. ③④ D. ②④
4. 如图,在 ABCD中,EF∥AD,HN∥AB,则图中的平行四边形共有 ( )
A. 12个 B. 9个 C. 7个 D. 5个
5. 如图,在 ABCD中,点E在AD上,且EC平分∠BED.若∠EBC=30°,BE=10,则 ABCD的面积为 .
6. 如图,在 ABCD中,点E、F分别在边AB、CD上,∠ADE=∠CBF,EF与BD相交于点O.求证:OB=OD.
第6题
考点三 矩形、菱形、正方形的性质与判定
7. 下列命题属于真命题的是 ( )
A. 对角线互相垂直的四边形是平行四边形 B. 对角线相等的四边形是矩形
C. 对角线互相平分的四边形是菱形 D. 对角线互相垂直的矩形是正方形
8. 如图,D、E、F分别是△ABC各边的中点,连接DE、DF,则下列说法错误的是 ( )
A. △BDE和△DCF的面积相等 B. 四边形AEDF是平行四边形
C. 若AB=BC,则四边形AEDF是菱形 D. 若∠A=90°,则四边形AEDF是矩形
9. 如图,菱形ABCD的对角线AC、BD的长分别为6、8,AE⊥BC于点E,则AE的长是 ( )
A. B. C. D.
10. (2023·临沂)若菱形的两条对角线长分别为6和8,则该菱形的面积为 .
11. 如图,M为正方形ABCD的对角线BD上的一点,连接AM并延长,交CD于点P.若PM=PC,则∠AMB的度数为 .
12. (2023·大庆)如图,在 ABCD中,E为线段CD的中点,连接AC、AE,延长AE、BC交于点F,连接DF,∠ACF=90°.
(1) 求证:四边形ACFD是矩形;
(2) 若CD=13,CF=5,则四边形ABCE的面积为 .
第12题
13. 如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.
(1) 求证:四边形AECD是菱形;
(2) 若AB=6,BC=10,求EF的长.
第13题
考点四 三角形的中位线
14. 如图,在△ABC中,D、E、F分别为各边的中点,AH是高,连接DH、DE、FH、FE.若∠DEF=65°,则∠DHF的度数为 ( )
A. 55° B. 60° C. 65° D. 70°
15. 如图,在矩形ABCD中,对角线AC、BD相交于点O,E是边AD的中点,点F在对角线AC上,且AF=AC,连接EF.若AC=10,则EF的长为 .
16. 如图,在四边形ABCD中,AC=BD=6,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2的值为 .
17. 如图,将菱形ABCD绕点A按逆时针方向旋转α得到菱形AB'C'D',∠B=β.当AC平分∠B'AC'时,α与β满足的数量关系是 ( )
A. α=2β B. 2α=3β C. 4α+β=180° D. 3α+2β=180°
18. 如图,在矩形ABCD中,AB=1,BC=2,点A在x轴正半轴上,点D在y轴正半轴上.当点A在x轴上运动时,点D也随之在y轴上运动,在这个运动过程中,点C到原点O的最大距离为 .
19. (2023·哈尔滨)已知四边形ABCD是平行四边形,点E在对角线BD上,点F在边BC上,连接AE、EF,DE=BF,BE=BC.
(1) 如图①,求证:△AED≌△EFB;
(2) 如图②,若AB=AD,AE≠ED,过点C作CH∥AE,交BE于点H,则图②中与∠BAE相等的角是 .
20. 如图,在四边形ABCD中,AB∥CD,AB=AD,CB=CD,E是CD上一点,BE交AC于点F,连接DF.
(1) 求证:四边形ABCD是菱形;
(2) 试确定点E的位置,使得∠BCD=∠EFD,并说明理由.
第20题
21. 已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM、EM.
(1) 如图①,点E在CD上,点G在BC的延长线上,请判断DM、EM的数量关系与位置关系,并直接写出结论.
(2) 如图②,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立 如果成立,请给出证明;如果不成立,请说明理由.
(3) 将图①中的正方形CEFG绕点C旋转,使D、E、F三点在一条直线上.若AB=13,CE=5,请画出图形,并直接写出MF的长.
第9章 中心对称图形——
平行四边形
1. B 2. C 3. A 4. B 5. 50
6. ∵ 四边形ABCD是平行四边形,∴ AB=CD,AD=CB,∠A=∠C.在△DAE和△BCF中,∴ △DAE≌△BCF.∴ DE=BF,AE=CF.∵ AB=CD,∴ AB-AE=CD-CF,即BE=DF.∴ 四边形BFDE是平行四边形.∴ OB=OD
7. D 8. C 9. C 10. 24 11. 75°
12. (1) ∵ 四边形ABCD是平行四边形,∴ AD∥BC.∴ ∠ADE=∠FCE,∠DAE=∠CFE.∵ E为线段CD的中点,∴ DE=CE.∴ △ADE≌△FCE.∴ AE=FE.∴ 四边形ACFD是平行四边形.∵ ∠ACF=90°,∴ 四边形ACFD是矩形 (2) 45
13. (1) ∵ AD∥BC,AE∥DC,∴ 四边形AECD是平行四边形.∵ 在Rt△BAC中,∠BAC=90°,E是BC的中点,∴ AE=BC=CE.∴ 四边形AECD是菱形 (2) 如图,过点A作AH⊥BC于点H.∵ ∠BAC=90°,AB=6,BC=10,∴ AC==8.∵ BC·AH=AB·AC=2S△BAC,∴ AH===.由(1),得四边形AECD是菱形,∴ CE=CD.∵ S菱形AECD=CE·AH=CD·EF,∴ EF=AH=
14. C 解析:利用三角形中位线定理,得DE∥AC,EF∥AB,由此得四边形ADEF是平行四边形,∴ ∠DEF=∠DAF.利用直角三角形斜边上的中线的性质可说明DH=DA,HF=AF,∴ ∠DAH=∠DHA,∠FAH=∠FHA,即∠DAF=∠DHF,从而可得∠DHF=∠DEF=65°.
15. 16. 36 17. C
18. 1+ 解析:取AD的中点H,连接CH、OH.由勾股定理可求CH=,由直角三角形斜边上中线的性质可求OH=AD=1.注意到CO≤OH+CH,由此可知当点O、H、C共线时,CO长取得最大值,最大值为OH+CH=1+.
19. (1) ∵ 四边形ABCD是平行四边形,∴ AD∥BC,AD=BC.∴ ∠ADE=∠EBF.∵ BC=BE,∴ AD=BE.在△AED和△EFB中,∴ △AED≌△EFB (2) ∠AEB、∠DHC、∠EFC、∠DCH
20. (1) 在△ABC和△ADC中,∴ △ABC≌△ADC.∴ ∠BAC=∠DAC.∵ AB∥CD,∴ ∠BAC=∠ACD.∴ ∠DAC=∠ACD.∴ AD=CD.∵ AB=AD,CB=CD,∴ AB=CB=CD=AD.∴ 四边形ABCD是菱形 (2) 当 BE⊥CD时,∠BCD=∠EFD 理由:由(1),得四边形ABCD是菱形,∴ ∠BCF=∠DCF.在△BCF和△DCF中,∴ △BCF≌△DCF.∴ ∠CBF=∠CDF.∵ BE⊥CD,∴ ∠BEC=∠DEF=90°.∴ 易得∠BCD=∠EFD.
21. (1) DM=EM,DM⊥EM (2) (1)中的结论仍然成立,即DM=EM,DM⊥EM 延长EM交DA的延长线于点H.∵ 四边形ABCD与四边形CEFG是正方形,∴ ∠ADE=∠DEF=90°,AD=CD,EC=FE.∴ ∠ADE+∠DEF=180°.∴ AD∥EF.∴ ∠MAH=∠MFE.∵ M是AF的中点,∴ AM=FM.又∵ ∠AMH=∠FME,∴ △AMH≌△FME.∴ MH=ME,AH=FE=EC.∴ DH=DE.∴ 在Rt△EDH中,DM=EM,DM⊥EM (3) 如图①,MF=;如图②,MF=
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
