专题(三) 中心对称图形——平行四边形(含答案) 2024-2025学年数学苏科版八年级下册
文档属性
| 名称 | 专题(三) 中心对称图形——平行四边形(含答案) 2024-2025学年数学苏科版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 213.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-03 20:17:42 | ||
图片预览

文档简介
专题(三) 中心对称图形——平行四边形
1.
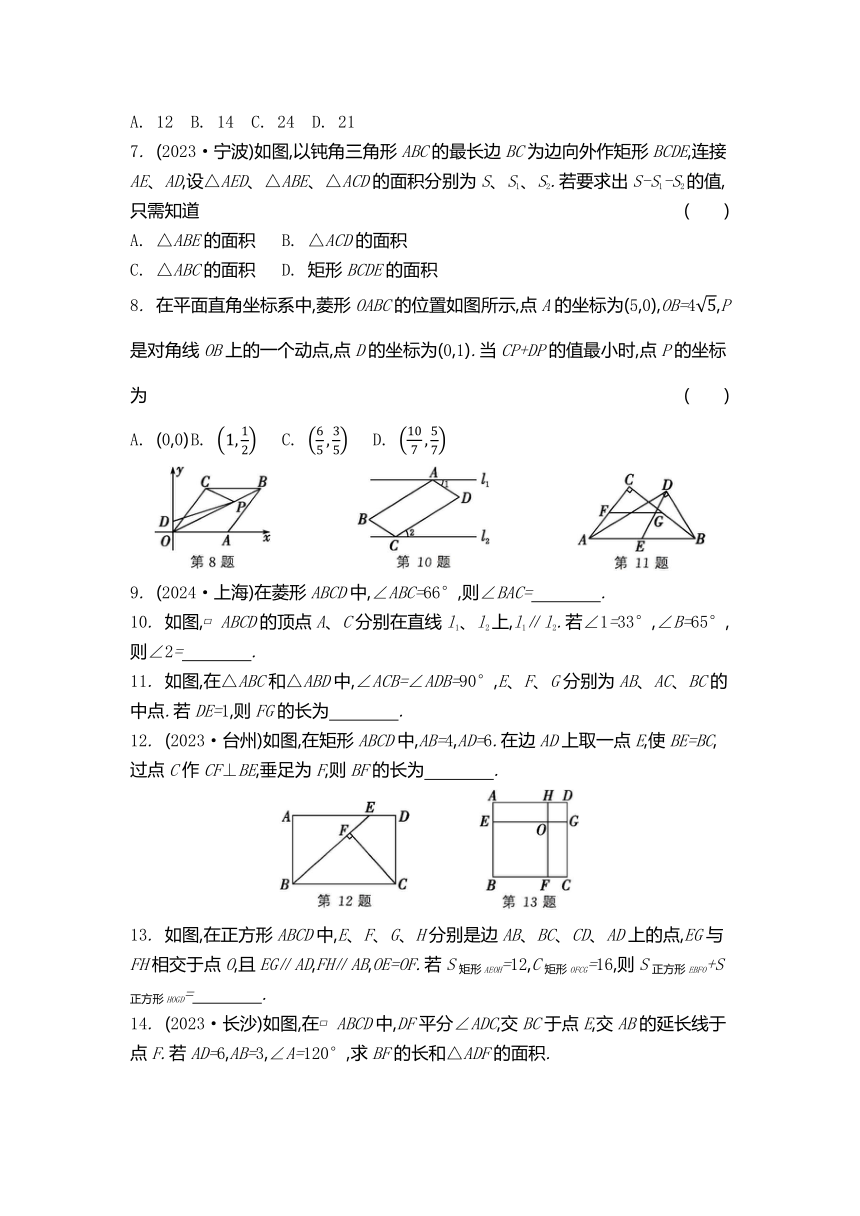
(2024·自贡)我国数学家赵爽在他所著《勾股圆方图注》中,运用如图所示的弦图巧妙地证明了勾股定理.下列关于“赵爽弦图”的说法中,正确的是( )
A. 是轴对称图形 B. 是中心对称图形
C. 既是轴对称图形,又是中心对称图形 D. 既不是轴对称图形,也不是中心对称图形
2. (2024·湖北)如图,在平面直角坐标系中,点A的坐标为(-4,6),将线段OA绕点O按顺时针方向旋转90°,则点A的对应点A'的坐标为 ( )
A. (4,6) B. (6,4) C. (-4,-6) D. (-6,-4)
3. 如图,O是 ABCD的对角线AC、BD的交点,EF过点O分别交AD、BC于点E、F,下列结论一定成立的是( )
A. OE=OF B. AE=BF C. ∠DOC=∠OCD D. ∠CFE=∠DEF
4. 如图,M、N分别是△ABC的边AB、AC的中点,∠A=65°,∠ANM=45°,则∠B的度数为( )
A. 20° B. 45° C. 65° D. 70°
5. 已知四边形ABCD是平行四边形,AC、BD相交于点O,下列结论错误的是 ( )
A. OA=OC,OB=OD
B. 当AB=CD时,四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD且AC⊥BD时,四边形ABCD是正方形
6. 如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E、F、G、H分别是AB、BD、CD、AC的中点,则四边形EFGH的周长为 ( )
A. 12 B. 14 C. 24 D. 21
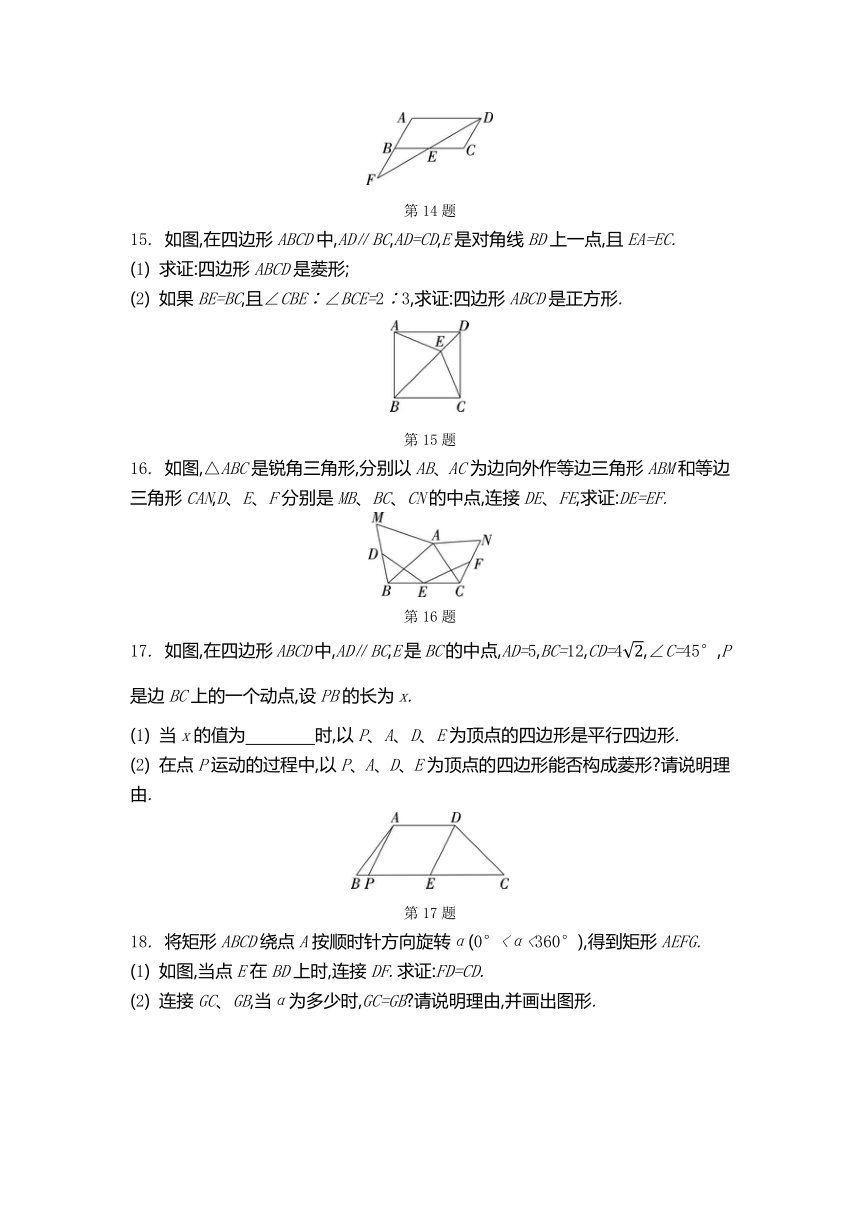
7. (2023·宁波)如图,以钝角三角形ABC的最长边BC为边向外作矩形BCDE,连接AE、AD,设△AED、△ABE、△ACD的面积分别为S、S1、S2.若要求出S-S1-S2的值,只需知道 ( )
A. △ABE的面积 B. △ACD的面积
C. △ABC的面积 D. 矩形BCDE的面积
8. 在平面直角坐标系中,菱形OABC的位置如图所示,点A的坐标为(5,0),OB=4,P是对角线OB上的一个动点,点D的坐标为(0,1).当CP+DP的值最小时,点P的坐标为 ( )
A. (0,0) B. C. D.
9. (2024·上海)在菱形ABCD中,∠ABC=66°,则∠BAC= .
10. 如图, ABCD的顶点A、C分别在直线l1、l2上,l1∥l2.若∠1=33°,∠B=65°,则∠2= .
11. 如图,在△ABC和△ABD中,∠ACB=∠ADB=90°,E、F、G分别为AB、AC、BC的中点.若DE=1,则FG的长为 .
12. (2023·台州)如图,在矩形ABCD中,AB=4,AD=6.在边AD上取一点E,使BE=BC,过点C作CF⊥BE,垂足为F,则BF的长为 .
13. 如图,在正方形ABCD中,E、F、G、H分别是边AB、BC、CD、AD上的点,EG与FH相交于点O,且EG∥AD,FH∥AB,OE=OF.若S矩形AEOH=12,C矩形OFCG=16,则S正方形EBFO+S正方形HOGD= .
14. (2023·长沙)如图,在 ABCD中,DF平分∠ADC,交BC于点E,交AB的延长线于点F.若AD=6,AB=3,∠A=120°,求BF的长和△ADF的面积.
第14题
15. 如图,在四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1) 求证:四边形ABCD是菱形;
(2) 如果BE=BC,且∠CBE∶∠BCE=2∶3,求证:四边形ABCD是正方形.
第15题
16. 如图,△ABC是锐角三角形,分别以AB、AC为边向外作等边三角形ABM和等边三角形CAN,D、E、F分别是MB、BC、CN的中点,连接DE、FE,求证:DE=EF.
第16题
17. 如图,在四边形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,CD=4,∠C=45°,P是边BC上的一个动点,设PB的长为x.
(1) 当x的值为 时,以P、A、D、E为顶点的四边形是平行四边形.
(2) 在点P运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形 请说明理由.
第17题
18. 将矩形ABCD绕点A按顺时针方向旋转α(0°<α<360°),得到矩形AEFG.
(1) 如图,当点E在BD上时,连接DF.求证:FD=CD.
(2) 连接GC、GB,当α为多少时,GC=GB 请说明理由,并画出图形.
第18题
19. 如图①,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.
(1) 如图②,将△ADF绕点A按顺时针方向旋转90°得到△ABG,求证:△AGE≌△AFE.
(2) 如图③,连接BD,交AE于点M,交AF于点N.请探究并猜想线段BM、MN、ND之间有什么数量关系,并说明理由.
专题(三) 中心对称图形——平行四边形
1. B 2. B 3. A 4. D 5. B 6. A
7. C 解析:如图,过点A作AG⊥ED于点G,交BC于点F,则四边形BFGE、四边形CDGF是矩形.∴ S-S1-S2=ED·AG-BE·EG-CD·DG=ED·AG-FG·ED=BC·AF=S△ABC,因此只需知道S△ABC,就可求出S-S1-S2的值.
8. D 9. 57° 10. 32° 11. 1 12. 2 13. 40
14. ∵ 四边形ABCD是平行四边形,∴ AB∥CD.∴ ∠CDE=∠F.∵ DF平分∠ADC,∴ ∠ADE=∠CDE.∴ ∠F=∠ADF.∴ AD=AF=6.∵ AB=3,∴ BF=AF-AB=3.过点D作DH⊥AF,交FA的延长线于点H,则∠H=90°. ∵ ∠BAD=120°,∠BAD=∠H+∠ADH,∴ ∠ADH=30°.∴ 在Rt△AHD中,AH=AD=3.∴ DH==3.∴ S△ADF=AF·DH=×6×3=9
15. (1) 在△ADE和△CDE中,∴ △ADE≌△CDE.∴ ∠ADE=∠CDE.∵ AD∥BC,∴ ∠ADE=∠CBD.∴ ∠CDE=∠CBD.∴ CD=BC.∵ AD=CD,∴ AD=BC.又∵ AD∥BC,∴ 四边形ABCD是平行四边形.又∵ AD=CD,∴ 四边形ABCD是菱形 (2) ∵ BE=BC,∴ ∠BEC=∠BCE.∵ ∠CBE∶∠BCE=2∶3,∴ ∠CBE=180°×=45°.由(1),得四边形ABCD是菱形,∴ ∠ABE=∠CBE=45°.∴ ∠ABC=90°.∴ 四边形ABCD是正方形
16. 如图,连接MC、BN.∵ △ABM和△CAN是等边三角形,∴ ∠BAM=∠CAN=60°,AM=AB,AC=AN.∴ ∠BAM+∠BAC=∠CAN+∠BAC,即∠MAC=∠BAN.在△MAC和△BAN中,∴ △MAC≌△BAN.∴ MC=BN.∵ D、E、F分别是MB、BC、CN的中点,∴ DE=MC,EF=BN.∴ DE=EF
17. (1) 1或11 (2) 能 理由:由(1),知当PB=11时,以P、A、D、E为顶点的四边形是平行四边形.∴ EP=AD=5.∵ E是BC的中点,∴ CE=BC=6.∴ PC=1.过点D作DF⊥BC于点F.在Rt△CDF中,∠DFC=90°,∠C=45°,∴ ∠C=∠CDF=45°.∴ CF=DF.∵ CD=4,∴ 由勾股定理,易得DF=FC=4.∴ FP=FC-PC=3.∴ 在Rt△PDF中,DP==5.∴ AD=DP.∴ 此时四边形PDAE是菱形,即以P、A、D、E为顶点的四边形能构成菱形.
18. (1) ∵ 矩形AEFG是由矩形ABCD旋转得到的,∴ AE=AB=CD,∠AEF=∠ABC=∠DAB=90°,FE=BC=AD.∴ ∠AEB=∠ABE.∴ ∠ABE+∠EDA=90°,∠AEB+∠DEF=180°-∠AEF=90°.∴ ∠EDA=∠DEF.又∵ DE=ED,AD=FE,∴ △AED≌△FDE.∴ AE=FD.∴ FD=CD (2) 当α=60°或300°时,GC=GB 理由:若GC=GB,则点G必在BC的垂直平分线上.分两种情况讨论:① 当点G在AD右侧时,如图①.设BC的垂直平分线GH交AD于点M,交BC于点H,连接DG.∵ 四边形ABCD是矩形,∴ BC=AD,BC∥AD,∠BCD=∠ADC=90°.∵ GH垂直平分BC,∴ ∠CHM=90°,CH=BC.∴ 四边形CHMD为矩形.∴ CH=DM,∠HMD=90°.∴ 易得DM=AD,GM⊥AD.∴ GM垂直平分AD.∴ AG=DG.由旋转的性质,得AD=AG,∴ AD=AG=DG.∴ △ADG是等边三角形.∴ ∠DAG=60°,即旋转角α=60°.② 当点G在AD左侧时,如图②.设BC的垂直平分线GH交BC于点H,交AD于点M,连接DG.同理,可得△ADG是等边三角形.∴ ∠DAG=60°.∴ 旋转角α=360°-60°=300°.综上所述,当α=60°或300°时,GC=GB.
19. (1) 由旋转的性质,知AG=AF,∠DAF=∠BAG,∠ABG=∠ADF=90°.∵ 四边形ABCD为正方形,∴ ∠ABC=90°,∠BAD=90°.∴ G、B、E三点共线.∵ ∠EAF=45°,∴ ∠BAE+∠DAF=45°.∴ ∠BAE+∠BAG=45°,即∠EAG=45°.∴ ∠EAG=∠EAF.又∵ AE=AE,∴ △AGE≌△AFE (2) MN2=ND2+BM2 理由:如图,将△ABM绕点A按逆时针方向旋转90°得到△ADM',连接NM'.∵ 四边形ABCD为正方形,∴ 易证∠ABD=∠ADB=45°,∠BAM+∠EAD=90°.由旋转的性质,知AM=AM',∠ABM=∠ADM'=45°,∠BAM=∠DAM',BM=DM'.∴ ∠NDM'=90°,∠DAM'+∠EAD=90°,即∠EAM'=90°.∴ 在Rt△NDM'中,M'N2=ND2+DM'2.∵ ∠EAM'=90°,∠EAF=45°,∴ ∠MAN=∠M'AN=45°.又∵ AN=AN,∴ △AMN≌△AM'N.∴ MN=M'N.又∵ BM=DM',∴ MN2=ND2+BM2.
1.
(2024·自贡)我国数学家赵爽在他所著《勾股圆方图注》中,运用如图所示的弦图巧妙地证明了勾股定理.下列关于“赵爽弦图”的说法中,正确的是( )
A. 是轴对称图形 B. 是中心对称图形
C. 既是轴对称图形,又是中心对称图形 D. 既不是轴对称图形,也不是中心对称图形
2. (2024·湖北)如图,在平面直角坐标系中,点A的坐标为(-4,6),将线段OA绕点O按顺时针方向旋转90°,则点A的对应点A'的坐标为 ( )
A. (4,6) B. (6,4) C. (-4,-6) D. (-6,-4)
3. 如图,O是 ABCD的对角线AC、BD的交点,EF过点O分别交AD、BC于点E、F,下列结论一定成立的是( )
A. OE=OF B. AE=BF C. ∠DOC=∠OCD D. ∠CFE=∠DEF
4. 如图,M、N分别是△ABC的边AB、AC的中点,∠A=65°,∠ANM=45°,则∠B的度数为( )
A. 20° B. 45° C. 65° D. 70°
5. 已知四边形ABCD是平行四边形,AC、BD相交于点O,下列结论错误的是 ( )
A. OA=OC,OB=OD
B. 当AB=CD时,四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD且AC⊥BD时,四边形ABCD是正方形
6. 如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E、F、G、H分别是AB、BD、CD、AC的中点,则四边形EFGH的周长为 ( )
A. 12 B. 14 C. 24 D. 21
7. (2023·宁波)如图,以钝角三角形ABC的最长边BC为边向外作矩形BCDE,连接AE、AD,设△AED、△ABE、△ACD的面积分别为S、S1、S2.若要求出S-S1-S2的值,只需知道 ( )
A. △ABE的面积 B. △ACD的面积
C. △ABC的面积 D. 矩形BCDE的面积
8. 在平面直角坐标系中,菱形OABC的位置如图所示,点A的坐标为(5,0),OB=4,P是对角线OB上的一个动点,点D的坐标为(0,1).当CP+DP的值最小时,点P的坐标为 ( )
A. (0,0) B. C. D.
9. (2024·上海)在菱形ABCD中,∠ABC=66°,则∠BAC= .
10. 如图, ABCD的顶点A、C分别在直线l1、l2上,l1∥l2.若∠1=33°,∠B=65°,则∠2= .
11. 如图,在△ABC和△ABD中,∠ACB=∠ADB=90°,E、F、G分别为AB、AC、BC的中点.若DE=1,则FG的长为 .
12. (2023·台州)如图,在矩形ABCD中,AB=4,AD=6.在边AD上取一点E,使BE=BC,过点C作CF⊥BE,垂足为F,则BF的长为 .
13. 如图,在正方形ABCD中,E、F、G、H分别是边AB、BC、CD、AD上的点,EG与FH相交于点O,且EG∥AD,FH∥AB,OE=OF.若S矩形AEOH=12,C矩形OFCG=16,则S正方形EBFO+S正方形HOGD= .
14. (2023·长沙)如图,在 ABCD中,DF平分∠ADC,交BC于点E,交AB的延长线于点F.若AD=6,AB=3,∠A=120°,求BF的长和△ADF的面积.
第14题
15. 如图,在四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1) 求证:四边形ABCD是菱形;
(2) 如果BE=BC,且∠CBE∶∠BCE=2∶3,求证:四边形ABCD是正方形.
第15题
16. 如图,△ABC是锐角三角形,分别以AB、AC为边向外作等边三角形ABM和等边三角形CAN,D、E、F分别是MB、BC、CN的中点,连接DE、FE,求证:DE=EF.
第16题
17. 如图,在四边形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,CD=4,∠C=45°,P是边BC上的一个动点,设PB的长为x.
(1) 当x的值为 时,以P、A、D、E为顶点的四边形是平行四边形.
(2) 在点P运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形 请说明理由.
第17题
18. 将矩形ABCD绕点A按顺时针方向旋转α(0°<α<360°),得到矩形AEFG.
(1) 如图,当点E在BD上时,连接DF.求证:FD=CD.
(2) 连接GC、GB,当α为多少时,GC=GB 请说明理由,并画出图形.
第18题
19. 如图①,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.
(1) 如图②,将△ADF绕点A按顺时针方向旋转90°得到△ABG,求证:△AGE≌△AFE.
(2) 如图③,连接BD,交AE于点M,交AF于点N.请探究并猜想线段BM、MN、ND之间有什么数量关系,并说明理由.
专题(三) 中心对称图形——平行四边形
1. B 2. B 3. A 4. D 5. B 6. A
7. C 解析:如图,过点A作AG⊥ED于点G,交BC于点F,则四边形BFGE、四边形CDGF是矩形.∴ S-S1-S2=ED·AG-BE·EG-CD·DG=ED·AG-FG·ED=BC·AF=S△ABC,因此只需知道S△ABC,就可求出S-S1-S2的值.
8. D 9. 57° 10. 32° 11. 1 12. 2 13. 40
14. ∵ 四边形ABCD是平行四边形,∴ AB∥CD.∴ ∠CDE=∠F.∵ DF平分∠ADC,∴ ∠ADE=∠CDE.∴ ∠F=∠ADF.∴ AD=AF=6.∵ AB=3,∴ BF=AF-AB=3.过点D作DH⊥AF,交FA的延长线于点H,则∠H=90°. ∵ ∠BAD=120°,∠BAD=∠H+∠ADH,∴ ∠ADH=30°.∴ 在Rt△AHD中,AH=AD=3.∴ DH==3.∴ S△ADF=AF·DH=×6×3=9
15. (1) 在△ADE和△CDE中,∴ △ADE≌△CDE.∴ ∠ADE=∠CDE.∵ AD∥BC,∴ ∠ADE=∠CBD.∴ ∠CDE=∠CBD.∴ CD=BC.∵ AD=CD,∴ AD=BC.又∵ AD∥BC,∴ 四边形ABCD是平行四边形.又∵ AD=CD,∴ 四边形ABCD是菱形 (2) ∵ BE=BC,∴ ∠BEC=∠BCE.∵ ∠CBE∶∠BCE=2∶3,∴ ∠CBE=180°×=45°.由(1),得四边形ABCD是菱形,∴ ∠ABE=∠CBE=45°.∴ ∠ABC=90°.∴ 四边形ABCD是正方形
16. 如图,连接MC、BN.∵ △ABM和△CAN是等边三角形,∴ ∠BAM=∠CAN=60°,AM=AB,AC=AN.∴ ∠BAM+∠BAC=∠CAN+∠BAC,即∠MAC=∠BAN.在△MAC和△BAN中,∴ △MAC≌△BAN.∴ MC=BN.∵ D、E、F分别是MB、BC、CN的中点,∴ DE=MC,EF=BN.∴ DE=EF
17. (1) 1或11 (2) 能 理由:由(1),知当PB=11时,以P、A、D、E为顶点的四边形是平行四边形.∴ EP=AD=5.∵ E是BC的中点,∴ CE=BC=6.∴ PC=1.过点D作DF⊥BC于点F.在Rt△CDF中,∠DFC=90°,∠C=45°,∴ ∠C=∠CDF=45°.∴ CF=DF.∵ CD=4,∴ 由勾股定理,易得DF=FC=4.∴ FP=FC-PC=3.∴ 在Rt△PDF中,DP==5.∴ AD=DP.∴ 此时四边形PDAE是菱形,即以P、A、D、E为顶点的四边形能构成菱形.
18. (1) ∵ 矩形AEFG是由矩形ABCD旋转得到的,∴ AE=AB=CD,∠AEF=∠ABC=∠DAB=90°,FE=BC=AD.∴ ∠AEB=∠ABE.∴ ∠ABE+∠EDA=90°,∠AEB+∠DEF=180°-∠AEF=90°.∴ ∠EDA=∠DEF.又∵ DE=ED,AD=FE,∴ △AED≌△FDE.∴ AE=FD.∴ FD=CD (2) 当α=60°或300°时,GC=GB 理由:若GC=GB,则点G必在BC的垂直平分线上.分两种情况讨论:① 当点G在AD右侧时,如图①.设BC的垂直平分线GH交AD于点M,交BC于点H,连接DG.∵ 四边形ABCD是矩形,∴ BC=AD,BC∥AD,∠BCD=∠ADC=90°.∵ GH垂直平分BC,∴ ∠CHM=90°,CH=BC.∴ 四边形CHMD为矩形.∴ CH=DM,∠HMD=90°.∴ 易得DM=AD,GM⊥AD.∴ GM垂直平分AD.∴ AG=DG.由旋转的性质,得AD=AG,∴ AD=AG=DG.∴ △ADG是等边三角形.∴ ∠DAG=60°,即旋转角α=60°.② 当点G在AD左侧时,如图②.设BC的垂直平分线GH交BC于点H,交AD于点M,连接DG.同理,可得△ADG是等边三角形.∴ ∠DAG=60°.∴ 旋转角α=360°-60°=300°.综上所述,当α=60°或300°时,GC=GB.
19. (1) 由旋转的性质,知AG=AF,∠DAF=∠BAG,∠ABG=∠ADF=90°.∵ 四边形ABCD为正方形,∴ ∠ABC=90°,∠BAD=90°.∴ G、B、E三点共线.∵ ∠EAF=45°,∴ ∠BAE+∠DAF=45°.∴ ∠BAE+∠BAG=45°,即∠EAG=45°.∴ ∠EAG=∠EAF.又∵ AE=AE,∴ △AGE≌△AFE (2) MN2=ND2+BM2 理由:如图,将△ABM绕点A按逆时针方向旋转90°得到△ADM',连接NM'.∵ 四边形ABCD为正方形,∴ 易证∠ABD=∠ADB=45°,∠BAM+∠EAD=90°.由旋转的性质,知AM=AM',∠ABM=∠ADM'=45°,∠BAM=∠DAM',BM=DM'.∴ ∠NDM'=90°,∠DAM'+∠EAD=90°,即∠EAM'=90°.∴ 在Rt△NDM'中,M'N2=ND2+DM'2.∵ ∠EAM'=90°,∠EAF=45°,∴ ∠MAN=∠M'AN=45°.又∵ AN=AN,∴ △AMN≌△AM'N.∴ MN=M'N.又∵ BM=DM',∴ MN2=ND2+BM2.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
