专题(五) 反比例函数(含答案) 2024-2025学年数学苏科版八年级下册
文档属性
| 名称 | 专题(五) 反比例函数(含答案) 2024-2025学年数学苏科版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 99.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-03 20:18:19 | ||
图片预览

文档简介
专题(五) 反比例函数
1. 下列函数中,变量y是x的反比例函数的为 ( )
A. y= B. xy=2 C. y= D. y=-
2. (2023·株洲)在反比例函数y=的图像上的点的坐标可以为 ( )
A. (1,-4) B. (4,-1) C. (2,4) D. (2,)
3. 已知点A(x1,y1)、B(x2,y2)都在反比例函数y=-的图像上,且x1<0A. y1>y2 B. y14. (2023·广州)已知正比例函数y1=ax的图像经过点(1,-1),反比例函数y2=的图像位于第一、三象限,则一次函数y=ax+b的图像一定不经过 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
5. 已知P(a,b)是反比例函数y=的图像上异于点(-1,-1)的一个动点,则+的值为 ( )
A. 2 B. 1 C. D.
第6题
6. (2024·龙东地区)如图,函数y=(x>0)的图像经过A、B两点,连接OA、AB,过点B作BD⊥y轴,垂足为D,BD交OA于点E,且E为OA的中点,则△AEB的面积是 ( )
A. 4.5 B. 3.5 C. 3 D. 2.5
7. (2023·青岛)反比例函数y=的图像经过点A,则反比例函数的表达式为 .
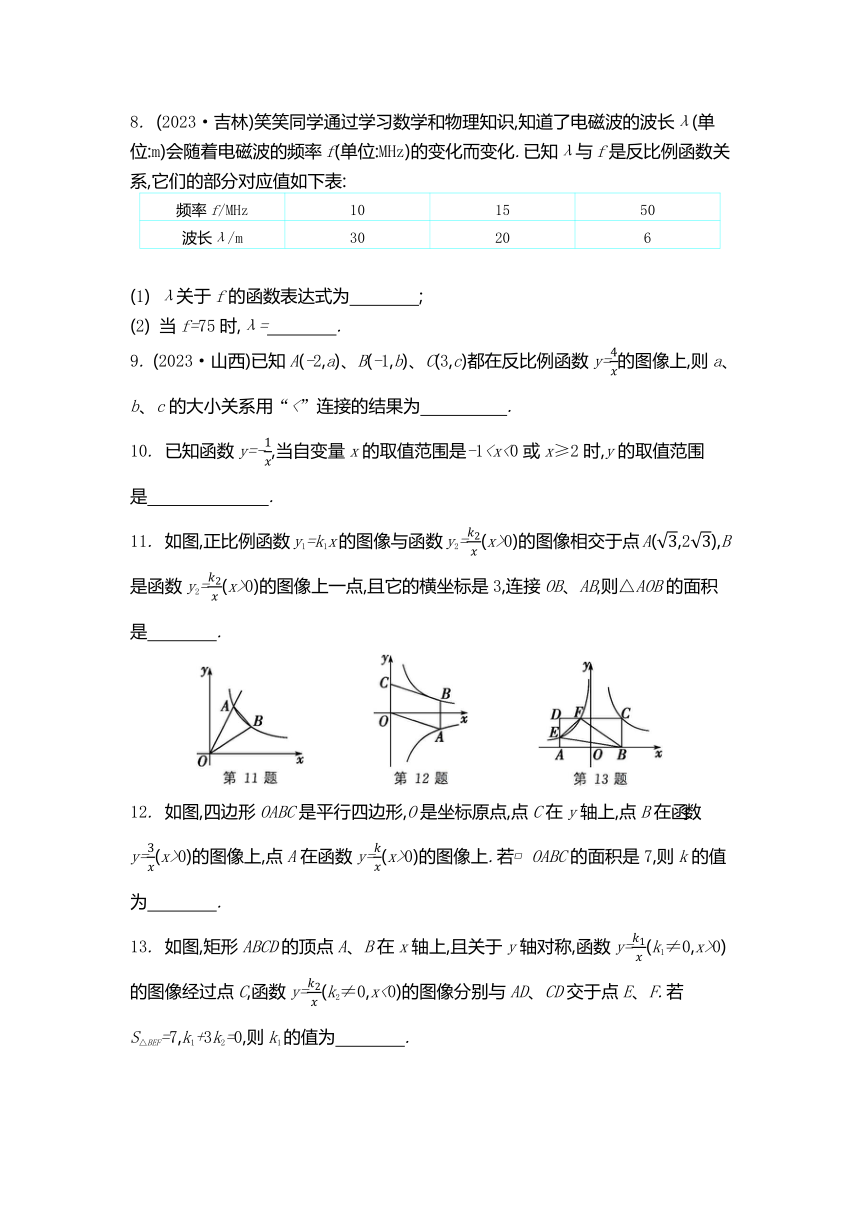
8. (2023·吉林)笑笑同学通过学习数学和物理知识,知道了电磁波的波长λ(单位:m)会随着电磁波的频率f(单位:MHz)的变化而变化.已知λ与f是反比例函数关系,它们的部分对应值如下表:
频率f/MHz 10 15 50
波长λ/m 30 20 6
(1) λ关于f的函数表达式为 ;
(2) 当f=75时,λ= .
9. (2023·山西)已知A(-2,a)、B(-1,b)、C(3,c)都在反比例函数y=的图像上,则a、b、c的大小关系用“<”连接的结果为 .
10. 已知函数y=-,当自变量x的取值范围是-111. 如图,正比例函数y1=k1x的图像与函数y2=(x>0)的图像相交于点A(,2),B是函数y2=(x>0)的图像上一点,且它的横坐标是3,连接OB、AB,则△AOB的面积是 .
12. 如图,四边形OABC是平行四边形,O是坐标原点,点C在y轴上,点B在函数y=(x>0)的图像上,点A在函数y=(x>0)的图像上.若 OABC的面积是7,则k的值为 .
13. 如图,矩形ABCD的顶点A、B在x轴上,且关于y轴对称,函数y=(k1≠0,x>0)的图像经过点C,函数y=(k2≠0,x<0)的图像分别与AD、CD交于点E、F.若S△BEF=7,k1+3k2=0,则k1的值为 .
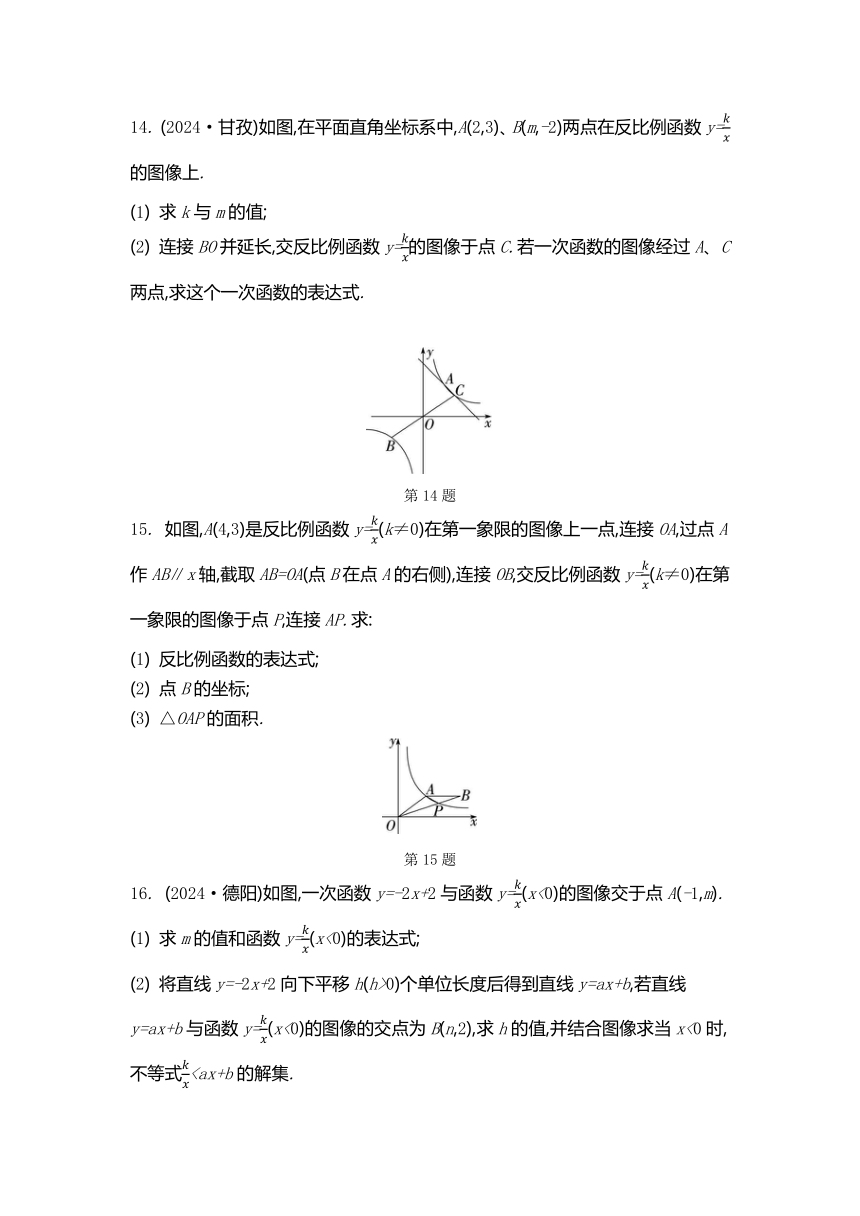
14. (2024·甘孜)如图,在平面直角坐标系中,A(2,3)、B(m,-2)两点在反比例函数y=的图像上.
(1) 求k与m的值;
(2) 连接BO并延长,交反比例函数y=的图像于点C.若一次函数的图像经过A、C两点,求这个一次函数的表达式.
第14题
15. 如图,A(4,3)是反比例函数y=(k≠0)在第一象限的图像上一点,连接OA,过点A作AB∥x轴,截取AB=OA(点B在点A的右侧),连接OB,交反比例函数y=(k≠0)在第一象限的图像于点P,连接AP.求:
(1) 反比例函数的表达式;
(2) 点B的坐标;
(3) △OAP的面积.
第15题
16. (2024·德阳)如图,一次函数y=-2x+2与函数y=(x<0)的图像交于点A(-1,m).
(1) 求m的值和函数y=(x<0)的表达式;
(2) 将直线y=-2x+2向下平移h(h>0)个单位长度后得到直线y=ax+b,若直线y=ax+b与函数y=(x<0)的图像的交点为B(n,2),求h的值,并结合图像求当x<0时,不等式第16题
17. 阅读下面的材料:
已知函数y=f(x),对于自变量x的取值范围内的任意x1、x2.
(1) 若x1(2) 若x1f(x2),则称f(x)是减函数.
例题:证明函数f(x)=(x>0)是减函数.
证明:设0∵ 00,x1x2>0.∴ >0,即f(x1)-f(x2)>0.
∴ f(x1)>f(x2).∴ 函数f(x)=(x>0)是减函数.
根据上述材料,解答下列问题:
已知函数f(x)=+x(x<0),例如:f(-2)=+(-2)=-.
(1) 计算:f(-3)= ,f(-4)= ;
(2) 猜想:函数f(x)=+x(x<0)是 函数(填“增”或“减”);
(3) 请仿照例题,证明(2)中的猜想.
18. 如图,A、B(-1,2)是一次函数y1=ax+b(a≠0)的图像与函数y2=(m≠0,x<0)的图像的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
(1) 在第二象限内,当y1-y2>0时,x的取值范围是 .
(2) 求一次函数的表达式及m的值.
(3) P是线段AB上一点,连接PC、PD.若△PCA和△PDB的面积相等,求点P的坐标.
(4) 若在y轴上存在点Q,使得QC-QB的值最大,则该最大值为 ,此时点Q的坐标为 .
第18题
专题(五) 反比例函数
1. B 2. D 3. A 4. C 5. B 6. A 7. y= 8. (1) λ= (2) 4 9. b1或-≤y<0
11. 2 12. -4
13. 9 解析:设点B的坐标为(m,0),由对称,得点A的坐标为(-m,0).由k1+3k2=0,得k2=-k1.先根据矩形ABCD,点C在函数y=(k1≠0,x>0)的图像上,点E、F在函数y=(k2≠0,x<0)的图像上,可表示出点C、E、F的坐标,再根据S△BEF=7,列方程求出k1的值.
14. (1) ∵ A(2,3)、B(m,-2)两点在反比例函数y=的图像上,∴ k=2×3=m×(-2).∴ k=6,m=-3 (2) 由(1),可知点B的坐标为(-3,-2).根据反比例函数图像的中心对称性,可得点C的坐标为(3,2).设直线AC对应的函数表达式为y=ax+b.将A(2,3)、C(3,2)代入,得解得∴ 这个一次函数的表达式为y=-x+5
15. (1) 将(4,3)代入y=,得3=,∴ k=12.∴ 反比例函数的表达式为y= (2) 如图,过点A作AC⊥x轴于点C.∵ 点A的坐标为(4,3),∴ OC=4,AC=3.∴ OA==5.∵ AB∥x轴,且AB=OA=5,∴ 点B的坐标为(9,3) (3) ∵ 点B的坐标为(9,3),∴ 易得直线OB对应的函数表达式为y=x.联立解得或(不合题意,舍去).∴ 点P的坐标为(6,2).如图,过点P作PD⊥x轴于点D,则OD=6,PD=2.∴ S△OAP=S△OCA+S梯形ACDP-S△ODP=×4×3+×(2+3)×(6-4)-×6×2=5
16. (1) ∵ 点A(-1,m)在一次函数y=-2x+2的图像上,∴ m=-2×(-1)+2=4.∴ A(-1,4).∵ 点A在函数y=(x<0)的图像上,∴ k=-4.∴ 函数y=(x<0)的表达式为y=-(x<0) (2) ∵ 点B(n,2)在函数y=-(x<0)的图像上,∴ 2=-,解得n=-2.∴ B(-2,2).将直线y=-2x+2向下平移h个单位长度后所得直线对应的函数表达式为y=-2x+2-h.∵ 点B(-2,2)在直线y=-2x+2-h上,∴ 2=-2×(-2)+2-h,解得h=4.根据函数图像及交点坐标可知,当x<0时,不等式17. (1) - - (2) 增 (3) 设x10.∴ (x1-x2)·<0,即f(x1)-f(x2)<0.∴ f(x1)18. (1) -4(4) 解析:利用待定系数法求出直线BC对应的函数表达式,要使QC-QB的值最大,则Q为直线BC与y轴的交点,最大值是BC的长.求出BC的长及点Q的坐标即可.
1. 下列函数中,变量y是x的反比例函数的为 ( )
A. y= B. xy=2 C. y= D. y=-
2. (2023·株洲)在反比例函数y=的图像上的点的坐标可以为 ( )
A. (1,-4) B. (4,-1) C. (2,4) D. (2,)
3. 已知点A(x1,y1)、B(x2,y2)都在反比例函数y=-的图像上,且x1<0
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
5. 已知P(a,b)是反比例函数y=的图像上异于点(-1,-1)的一个动点,则+的值为 ( )
A. 2 B. 1 C. D.
第6题
6. (2024·龙东地区)如图,函数y=(x>0)的图像经过A、B两点,连接OA、AB,过点B作BD⊥y轴,垂足为D,BD交OA于点E,且E为OA的中点,则△AEB的面积是 ( )
A. 4.5 B. 3.5 C. 3 D. 2.5
7. (2023·青岛)反比例函数y=的图像经过点A,则反比例函数的表达式为 .
8. (2023·吉林)笑笑同学通过学习数学和物理知识,知道了电磁波的波长λ(单位:m)会随着电磁波的频率f(单位:MHz)的变化而变化.已知λ与f是反比例函数关系,它们的部分对应值如下表:
频率f/MHz 10 15 50
波长λ/m 30 20 6
(1) λ关于f的函数表达式为 ;
(2) 当f=75时,λ= .
9. (2023·山西)已知A(-2,a)、B(-1,b)、C(3,c)都在反比例函数y=的图像上,则a、b、c的大小关系用“<”连接的结果为 .
10. 已知函数y=-,当自变量x的取值范围是-1
12. 如图,四边形OABC是平行四边形,O是坐标原点,点C在y轴上,点B在函数y=(x>0)的图像上,点A在函数y=(x>0)的图像上.若 OABC的面积是7,则k的值为 .
13. 如图,矩形ABCD的顶点A、B在x轴上,且关于y轴对称,函数y=(k1≠0,x>0)的图像经过点C,函数y=(k2≠0,x<0)的图像分别与AD、CD交于点E、F.若S△BEF=7,k1+3k2=0,则k1的值为 .
14. (2024·甘孜)如图,在平面直角坐标系中,A(2,3)、B(m,-2)两点在反比例函数y=的图像上.
(1) 求k与m的值;
(2) 连接BO并延长,交反比例函数y=的图像于点C.若一次函数的图像经过A、C两点,求这个一次函数的表达式.
第14题
15. 如图,A(4,3)是反比例函数y=(k≠0)在第一象限的图像上一点,连接OA,过点A作AB∥x轴,截取AB=OA(点B在点A的右侧),连接OB,交反比例函数y=(k≠0)在第一象限的图像于点P,连接AP.求:
(1) 反比例函数的表达式;
(2) 点B的坐标;
(3) △OAP的面积.
第15题
16. (2024·德阳)如图,一次函数y=-2x+2与函数y=(x<0)的图像交于点A(-1,m).
(1) 求m的值和函数y=(x<0)的表达式;
(2) 将直线y=-2x+2向下平移h(h>0)个单位长度后得到直线y=ax+b,若直线y=ax+b与函数y=(x<0)的图像的交点为B(n,2),求h的值,并结合图像求当x<0时,不等式
17. 阅读下面的材料:
已知函数y=f(x),对于自变量x的取值范围内的任意x1、x2.
(1) 若x1
例题:证明函数f(x)=(x>0)是减函数.
证明:设0
∴ f(x1)>f(x2).∴ 函数f(x)=(x>0)是减函数.
根据上述材料,解答下列问题:
已知函数f(x)=+x(x<0),例如:f(-2)=+(-2)=-.
(1) 计算:f(-3)= ,f(-4)= ;
(2) 猜想:函数f(x)=+x(x<0)是 函数(填“增”或“减”);
(3) 请仿照例题,证明(2)中的猜想.
18. 如图,A、B(-1,2)是一次函数y1=ax+b(a≠0)的图像与函数y2=(m≠0,x<0)的图像的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
(1) 在第二象限内,当y1-y2>0时,x的取值范围是 .
(2) 求一次函数的表达式及m的值.
(3) P是线段AB上一点,连接PC、PD.若△PCA和△PDB的面积相等,求点P的坐标.
(4) 若在y轴上存在点Q,使得QC-QB的值最大,则该最大值为 ,此时点Q的坐标为 .
第18题
专题(五) 反比例函数
1. B 2. D 3. A 4. C 5. B 6. A 7. y= 8. (1) λ= (2) 4 9. b
11. 2 12. -4
13. 9 解析:设点B的坐标为(m,0),由对称,得点A的坐标为(-m,0).由k1+3k2=0,得k2=-k1.先根据矩形ABCD,点C在函数y=(k1≠0,x>0)的图像上,点E、F在函数y=(k2≠0,x<0)的图像上,可表示出点C、E、F的坐标,再根据S△BEF=7,列方程求出k1的值.
14. (1) ∵ A(2,3)、B(m,-2)两点在反比例函数y=的图像上,∴ k=2×3=m×(-2).∴ k=6,m=-3 (2) 由(1),可知点B的坐标为(-3,-2).根据反比例函数图像的中心对称性,可得点C的坐标为(3,2).设直线AC对应的函数表达式为y=ax+b.将A(2,3)、C(3,2)代入,得解得∴ 这个一次函数的表达式为y=-x+5
15. (1) 将(4,3)代入y=,得3=,∴ k=12.∴ 反比例函数的表达式为y= (2) 如图,过点A作AC⊥x轴于点C.∵ 点A的坐标为(4,3),∴ OC=4,AC=3.∴ OA==5.∵ AB∥x轴,且AB=OA=5,∴ 点B的坐标为(9,3) (3) ∵ 点B的坐标为(9,3),∴ 易得直线OB对应的函数表达式为y=x.联立解得或(不合题意,舍去).∴ 点P的坐标为(6,2).如图,过点P作PD⊥x轴于点D,则OD=6,PD=2.∴ S△OAP=S△OCA+S梯形ACDP-S△ODP=×4×3+×(2+3)×(6-4)-×6×2=5
16. (1) ∵ 点A(-1,m)在一次函数y=-2x+2的图像上,∴ m=-2×(-1)+2=4.∴ A(-1,4).∵ 点A在函数y=(x<0)的图像上,∴ k=-4.∴ 函数y=(x<0)的表达式为y=-(x<0) (2) ∵ 点B(n,2)在函数y=-(x<0)的图像上,∴ 2=-,解得n=-2.∴ B(-2,2).将直线y=-2x+2向下平移h个单位长度后所得直线对应的函数表达式为y=-2x+2-h.∵ 点B(-2,2)在直线y=-2x+2-h上,∴ 2=-2×(-2)+2-h,解得h=4.根据函数图像及交点坐标可知,当x<0时,不等式
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
