2.7二次根式学案
图片预览

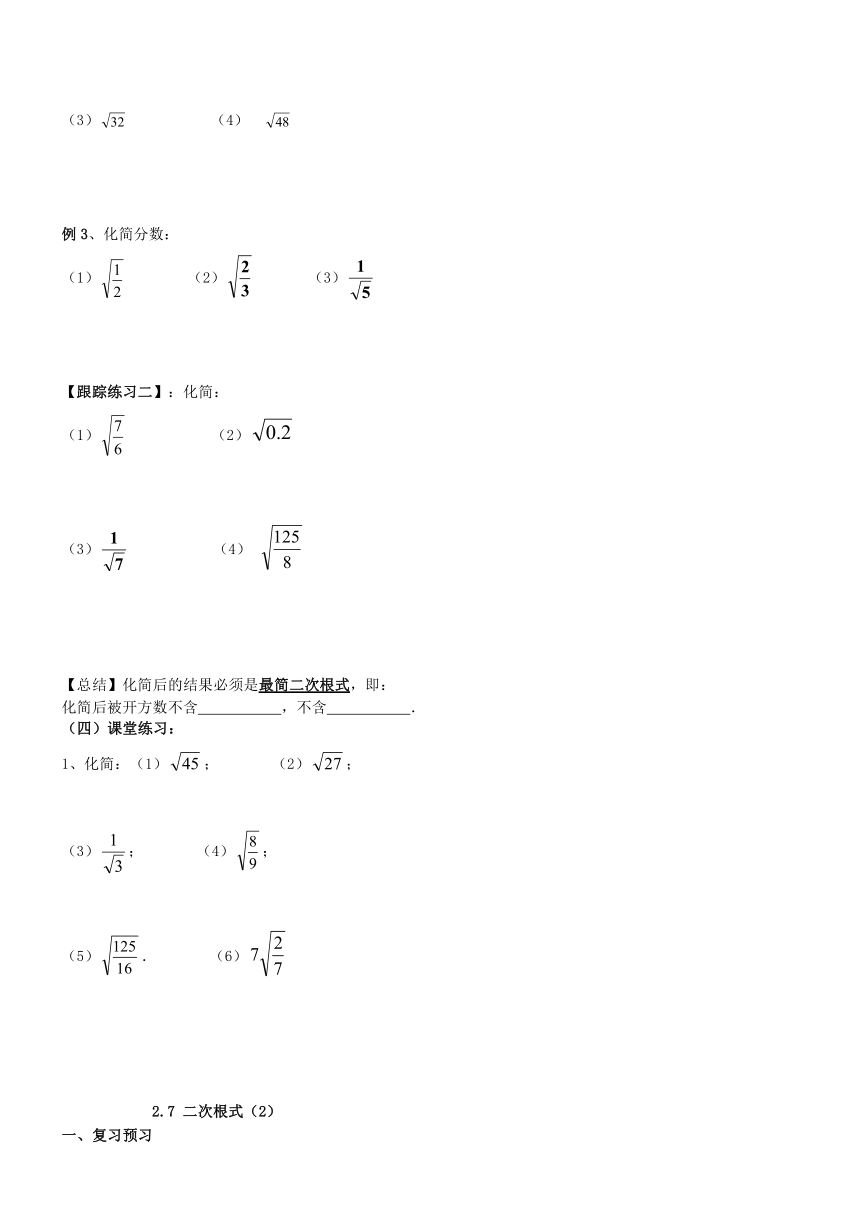

文档简介
2.7 二次根式(1)
(一)概念明晰:
1、思考:
,,,,(其中b=24,c=25),上述式子有什么共同特征?
___________________________________________
2、二次根式定义:一般形如___________的代数式叫做二次根式。
(二)探索性质:
1、尝试计算:
= ,= ;
= ,= ;
= ,= ;
= ,= .
2、总结归纳:
(a≥0,b≥0),
积的算术平方根,等于___________________
(a≥0, b>0)
商的算术平方根,等于___________________
(三)知识巩固:
例1 、化简(1); (2);
(3) (4)
例2、化简大数:(1) (2)
【跟踪练习一】:化简:
(1) (2)
(3) (4)
例3、化简分数:
(1) (2) (3)
【跟踪练习二】:化简:
(1) (2)
(3) (4)
【总结】化简后的结果必须是最简二次根式,即:
化简后被开方数不含 ,不含 .
(四)课堂练习:
1、化简:(1); (2);
(3); (4);
(5). (6)
2.7 二次根式(2)
一、复习预习
1、二次根式性质
(a____0,b____0),
(a____0, b____0)
2、对调等式的左右两边即可得:
二次根式乘法公式:
二次根式除法公式:
二、学习新课
例1、计算:
(1);(2);(3)
<小练习>化简:
例2、计算:
(1)3 (2);
(3); (4);
(5); (6)。
2、二次根式加减法:
(1)计算:
[小结]: + ___
-___
(2)计算:
[小结]:1.当被开方数相同时,可类似合并同类项,
只把______相加减,___ __不变。即:合并时必须
是同类二次根式(化简后,___________相同。)
2.当被开方数不相同时,两个根式_______合并.
例3、(1); (2);
(3)
【小结】:1.注意运算顺序. 2.结果应是最简形式.
三、课堂练习:
; ;
; ;
; ;
;
2.7 二次根式(3)
一、复习预习
1、乘法公式:
除法公式:
二、学习新课
例1、化简:
(1) (2)
(3) (4)
【跟踪练习一】:化简:
(1) (2)
(3) (4)
例2、计算:
(1); (2);
(3).
(4)+—
【跟踪练习二】:化简:
(1); (2);
(3). ( 4)2+—
(5)— (6)—+
(7)(+)× (8)+—
(一)概念明晰:
1、思考:
,,,,(其中b=24,c=25),上述式子有什么共同特征?
___________________________________________
2、二次根式定义:一般形如___________的代数式叫做二次根式。
(二)探索性质:
1、尝试计算:
= ,= ;
= ,= ;
= ,= ;
= ,= .
2、总结归纳:
(a≥0,b≥0),
积的算术平方根,等于___________________
(a≥0, b>0)
商的算术平方根,等于___________________
(三)知识巩固:
例1 、化简(1); (2);
(3) (4)
例2、化简大数:(1) (2)
【跟踪练习一】:化简:
(1) (2)
(3) (4)
例3、化简分数:
(1) (2) (3)
【跟踪练习二】:化简:
(1) (2)
(3) (4)
【总结】化简后的结果必须是最简二次根式,即:
化简后被开方数不含 ,不含 .
(四)课堂练习:
1、化简:(1); (2);
(3); (4);
(5). (6)
2.7 二次根式(2)
一、复习预习
1、二次根式性质
(a____0,b____0),
(a____0, b____0)
2、对调等式的左右两边即可得:
二次根式乘法公式:
二次根式除法公式:
二、学习新课
例1、计算:
(1);(2);(3)
<小练习>化简:
例2、计算:
(1)3 (2);
(3); (4);
(5); (6)。
2、二次根式加减法:
(1)计算:
[小结]: + ___
-___
(2)计算:
[小结]:1.当被开方数相同时,可类似合并同类项,
只把______相加减,___ __不变。即:合并时必须
是同类二次根式(化简后,___________相同。)
2.当被开方数不相同时,两个根式_______合并.
例3、(1); (2);
(3)
【小结】:1.注意运算顺序. 2.结果应是最简形式.
三、课堂练习:
; ;
; ;
; ;
;
2.7 二次根式(3)
一、复习预习
1、乘法公式:
除法公式:
二、学习新课
例1、化简:
(1) (2)
(3) (4)
【跟踪练习一】:化简:
(1) (2)
(3) (4)
例2、计算:
(1); (2);
(3).
(4)+—
【跟踪练习二】:化简:
(1); (2);
(3). ( 4)2+—
(5)— (6)—+
(7)(+)× (8)+—
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
