期中考试真题分类汇编 03 填空题 (含答案+解析)---2024-2025学年冀教版五年级数学下册
文档属性
| 名称 | 期中考试真题分类汇编 03 填空题 (含答案+解析)---2024-2025学年冀教版五年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 123.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-04 10:18:51 | ||
图片预览




文档简介
2024-2025学年冀教版五年级数学下册
期中考试真题分类汇编 03 填空题
一、填空题
1.(2024五下·湛江期中)一个长方体的长是15 dm ,宽是5dm ,高是长的,这个长方体的体积是 dm,表面积是 dm。
2.(2024五下·威县期中)张叔叔承包了一片山地,他准备用这片山地的 种农作物, 种果树。如果农作物的 是玉米, 玉米地占整块地的 , 如果果树的 是枣树, 枣树占整块地的 。
3.(2024五下·高邮期中) 若a=b+1(a、b都是大于0的自然数),则a和b的最大公因数是 ,最小公倍数是 。
4.(2022五下·巧家期中) = = =45÷ = (填带分数)= (填小数)。
5.(2024五下·薛城期中)
(1)把一条1米长的彩带平均分成5份,每份长 米。
(2)把一条2米长的彩带平均分成5份,每份是 个 米,是 米。
6.(2024五下·德州期中)a=2×5×m,b=3×5×m(m是不为0的自然数),如果a和b的最大公因数是65,那么a和b的最小公倍数是 。
7.(2024五下·章贡期中)已知A=2x3x3x5,B=2x2x5,C=3x3x5,那么A,B,C的最大公因数是 ,最小公倍数是 。
8.(2024五下·霞山期中)正方体的棱长总和是48厘米,它的棱长是 厘米。
9.(2024五下·墨玉期中) 2.5L= mL 12dm3= cm3
3.85m3= dm3 785mL= cm3= dm3
10.(2023五下·阳山期中)正方体的棱长扩大到原来的3倍,棱长总和扩大到原来的 倍,表面积扩大到原来的 倍,体积扩大到原来的 倍。
11.(2024五下·龙岗期中)2÷ =× =+ =0.25=- 。
12.(2024五下·安阳期中)如图,将一个正方体的棱长从2cm增加到4cm,它的棱长总和扩大到原来的 倍,表面积扩大到原来的 倍,体积扩大到原来的 倍。
13.(2024五下·万载期中)一根6m长的方钢,把它横截成3段时,表面积增加120cm2,原来方钢的体积是 。
14.(2024五下·兰溪期中)320cm2= m2 6.25L= mL
5.2m= m cm 60mL= L
15.(2024五下·隆回期中)a÷b=8,那么a和b的最大公因数是 ,最小公倍数是 。
16.(2024五下·汉川期中)修路队要用216立方米的沙子铺路,铺的路宽2米,要铺3厘米厚,这些沙子一共能铺 长的路。
17.(2024五下·汉川期中)在横线上填上合适的单位名称.。
一个苹果的体积约130 一大瓶可乐的容积是2
18.(2024五下·汉川期中)下图是一个正方体表面的展开图,每面都标有数字。在正方体中,数字“3”对面的数字是 ,相交于同一个顶点的三个面上的数字之和最小是 。
19.(2024五下·苍南期中)如图是一个长方体展开图。
(1)如果长方形B在下面,那么长方形 在上面;如果长方形C在前面,那么长方形 在后面。
(2)根据图中的数据(单位:dm),这个长方体的体积是 dm3。
20.(2024五下·邯郸期中)与 互为倒数,最小合数的倒数是 。
21.(2024五下·电白期中)8.5m3= dm3 L
22.(2024五下·蕲春期中)一个正方体的棱长和是36cm,它的体积是 ,表面积是 .
23.(2024五下·陆丰期中)一个长方体相交于一个顶点的三条棱分别长9cm、7cm和6cm,它的表面积是 cm2,体积是 cm3。
24.(2024五下·陆丰期中)把4L水平均装在5个瓶子里,每个瓶子里的水占这些水的 ,每瓶水有 升。
25.(2024五下·陆丰期中)一个三位数既有因数2,又有因数3,同时又是5的倍数,这个数最小是 。
26.(2024五下·陆丰期中)填上合适的单位。
一桶色拉油的容积是5 , 一支铅笔的长约15
一块橡皮的体积约为6 一盒牛奶的体积约250
27.(2024五下·陆丰期中)5200dm3= m3 4.08dm3= L mL。
28.(2024五下·陆丰期中)一个长方体的长、宽、高都扩大为原来的2倍,则表面积扩大为原来的 倍,体积扩大为原来的 倍。
29.(2024五下·电白期中)看图填一填。
- +
30.(2024五下·广州期中)9.8升= 毫升= 立方厘米
3.2米= 分米
2.1平方分米= 平方米
31.(2024五下·广州期中)在横线里填入合适的单位。
集装箱的体积约是40 ,一瓶纯净水约500 ,
操场的面积约是2000 ,游泳池水深2 。
32.(2024五下·桑植期中) = =8÷ = (填小数)。
33.(2024五下·茂名期中)在横线上填合适的分数。
53分= 时 13克= 千克
8dm3= L 360dm2= m2
7100dm3= m3 2.08m3= m3 dm3
34.(2024五下·茂名期中)一个正方体的棱长之和是36dm,这个正方体的表面积是
35.(2024五下·汝城期中) 若是假分数,是真分数, 则m一定是 。
36.(2024五下·汝城期中)的分数单位是 ,它里面有 个这样的分数单位,再添上 个这样的分数单位就是最小的合数。
37.(2024五下·汝城期中) 做一个底面周长26cm,高5cm的长方体框架,至少要 cm铁丝。
38.(2024五下·汝城期中) ÷16= = (填小数)。
39.(2024五下·临平期中)一个透明的塑料盒里装满了体积为1cm3的小正方体。它的容积是 cm3,李老师从盒里拿出一些准备在数学课上用,还剩下一部分(如图),李老师拿出了 个小正方体。
40.(2024五下·临平期中)要搭成一个正方体框架,还需要 个磁力珠和 根磁力棒。
41.(2024五下·辰溪期中)10.8m2= dm2 886mL= cm3= dm3
2700 cm3= m3 9.87L= L mL
42.(2024五下·电白期中)用一根24dm长的铁丝焊成一个正方体框架,这个正方体的表面积是 ,体积是
。
43.(2024五下·怀化期中) 在中,当a= 时,这个分数可以化成最小假分数;当a= 时,它是最大的真分数。
44.(2024五下·汝城期中)3050cm2= dm2 cm3
dm3 5600mL= L mL
45.(2024五下·电白期中)在横线上填上合适的小数或分数。
= 1.5=
46.(2024五下·电白期中)把5个棱长为3cm的正方体木块放在墙角处(如下图)有 个面露在外面,露在外面的面积是 cm2。
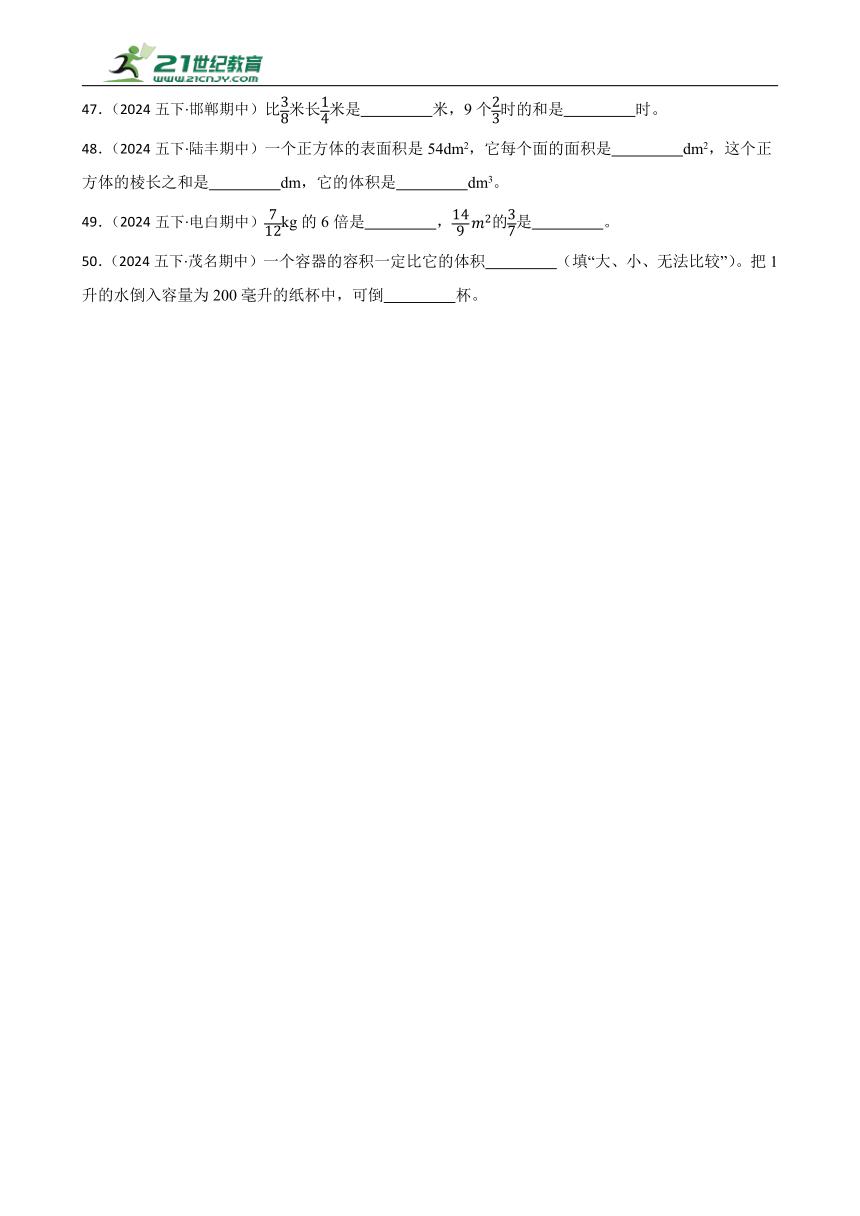
47.(2024五下·邯郸期中)比米长米是 米,9个时的和是 时。
48.(2024五下·陆丰期中)一个正方体的表面积是54dm2,它每个面的面积是 dm2,这个正方体的棱长之和是 dm,它的体积是 dm3。
49.(2024五下·电白期中)kg的6倍是 ,的是 。
50.(2024五下·茂名期中)一个容器的容积一定比它的体积 (填“大、小、无法比较”)。把1升的水倒入容量为200毫升的纸杯中,可倒 杯。
答案解析部分
1.225;270
解:高:15×=3(dm);
体积:15×5×3=225(dm3);
表面积:(15×5+15×3+5×3)×2
=(75+45+15)×2
=135×2
=270(dm2)
故答案为:225;270。
长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高,先求出高,然后分别求出体积和表面积即可。
2.;
解:×=
×=。
故答案为:;。
玉米地占整块地的分率=农作物占的分率×玉米占的分率,枣树占整块地的分率=果树占的分率×枣树占的分率。
3.1;ab
解:a和b的最大公因数是1,最小公倍数是ab;
故答案为:1;ab。
相邻自然数的最大公因数恒为1,最小公倍数为两数之积,据此求解。
4.25;24;36;;1.25
解:20×=25;30÷=24;45÷=36;=;=5÷4=1.25。
故答案为:25;24;36;;1.25。
分子=分母×分数值;分母=分子×分数值;除数=被除数÷商;分数化小数:用分子除以分母,商写成小数的形式。
5.(1)
(2)2; ;
解:(1)1÷5=(米);
(2)把一条2米长的彩带平均分成5份,每份是2个米,是米。
故答案为:;2;;。
(1)求每份的长度,用总长度除以份数即可解答;(2)2米里面有2个1米,平均分成的份数相同,那么,2米平均分成5份,每份的长度就是2个第一小题中每份长度。据此解答。
6.390
解:如果a=2×5×m,b=3×5×m(m是不为0的自然数),则a和b的最大公因数是5×m,
5×m=65
5×m÷5=65÷5
m=13
a=2×5×13;
b=3×5×13;
a和b的最小公倍数是:5×13×2×3=390
故答案为:390。
用分解质因数的方法求两个数的最大公因数,先把每个数分别分解质因数,再把两个数中的全部公有质因数提取出来连乘,所得的积就是这两个数的最大公因数;
用分解质因数的方法求两个数的最小公倍数,先把每个数分别分解质因数,把这两个数公有的质因数和各自独有的质因数相乘,它们的乘积就是这两个数的最小公倍数,据此解答。
7.5;180
解:A=2×3×3×5=90
B=2×2×5=20
C=3×3×5=45
A,B,C的最大公因数是5,最小公倍数是5×2×3×3×2=180。
故答案为:5;180。
先求出A=90,B=20,C=45,然后用短除法求出A,B,C的最大公因数、最小公倍数。
8.4
解:48÷12=4(厘米)。
故答案为:4。
正方体的棱长=正方体的棱长和÷12。
9.2500;12000;3850;785;0.785
解:2.5×1000=2500,所以 2.5升=2500毫升
12×1000=12000,所以12立方分米=12000立方厘米
3.85×1000=3850,所以3.85立方米=3850立方分米
785÷1000=0.785,所以 785毫升=785立方厘米=0.785立方分米
故答案为:2500;12000;3850;785;0.785。
1升=1000毫升,1立方分米=1000立方厘米,1立方米=1000立方分米,1毫升=1立方厘米,1立方分米=1000立方厘米;把高级单位换算成低级单位要乘进率,把低级单位换算成高级单位要除以进率。
10.3;9;27
解:3×1=3
3×3=9
3×3×3=27。
故答案为:3;9;27。
正方体的棱长和=棱长×12;正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长。正方体的棱长扩大到原来的3倍,棱长总和扩大到原来的3倍,表面积扩大到原来的9倍,体积扩大到原来的27倍。
11.8;;;
2÷0.25=8;
0.25÷=;
0.25-=0
-0.25=。
故答案为:8;;;。
除数=被除数÷商;一个因数=积÷另一个因数;一个加数=和-另一个加数;减数=被减数-差。
12.2;4;8
解:4÷2=2,棱长扩大到原来的2倍,
=2×2=4,=2×2×2=8,
它的棱长总和扩大到原来的2倍,表面积扩大到原来的4倍,体积扩大到原来的8倍。
故答案为:2;4;8。
正方体的棱长扩大到原来的n倍,棱长总和扩大到原来的n倍,表面积扩大到原来的n的平方倍,体积扩大到原来的n的立方倍。
13.18000立方厘米
解:6米=600厘米
120÷4×600
=30×600
=18000(立方厘米)。
故答案为:18000立方厘米。
原来方钢的体积=底面积×方钢的长,其中,底面积=增加的表面积÷增加面的个数。
14.0.032;6250;5;20;0.06
解:320÷10000=0.032(平方米),所以320平方厘米=0.032平方米;
6.25×1000=6250(毫升),所以6.25升=6250毫升;
(5.2-5)×100
=0.2×100
=20(厘米),所以5.2米=5米20厘米;
60÷1000=0.06(升),所以60毫升=0.06升。
故答案为:0.032;6250;5;20;0.06。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
15.b;a
解:a÷b=8,可知a和b是倍数关系,所以a和b的最大公因数是b,最小公倍数是a。
故答案为:b;a。
两数是倍数关系,最大公因数是较小数,最小公倍数是较大数。
16.3600
解:3厘米=0.03米
216÷(2×0.03)
=216÷0.06
=3600(米)。
故答案为:3600。
先单位换算3厘米=0.03米,这些沙子一共能铺路的长度=沙子的体积÷(要修路的宽×厚度)。
17.立方厘米;升
解:一个苹果的体积约130立方厘米;
一大瓶可乐的容积是2升。
故答案为:立方厘米;升。
根据实际生活经验以及题干中的具体数据来进行填空。
18.2;7
解:数字“3”对面的数字是2,数字1对面的数字是5,数字4对面的数字是6。
相交于同一个顶点的三个面上的数字之和最小是: 1、2、4相交于一个顶点,和是1+2+4=7。
故答案为:2;7。
正方体展开图的规律:中间四个成一行,两边各一无规矩;二三紧连错一个,三一相连一随意;两两相连各错一,三个两排一对齐;一条线上不过四,田七和凹要放弃;相间之端是对面,间二拐角面相邻。
相交于同一个顶点的三个面上的数字之和最小,即是找出两两相邻的三个面上的数字最小的面,即1、2、4,计算即可。
19.(1)E;F
(2)24
解:(1)如果长方形B在下面,那么长方形E在上面;如果长方形C在前面,那么长方形F在后面;
(2)4×3×2=24(立方分米)。
故答案为:(1)E;F;(2)24。
(1)长方体相对的面不相邻,则B和E相对,C和F相对,A和D相对;
(2)长方体的体积=长×宽×高。
20.;
解:1÷=
1÷4=。
故答案为:;。
最小的合数是4,求一个数0除外的倒数=1÷这个数。
21.8500;350
解:8.5×1000=8500dm3, 8.5m3=8500dm3 ;
dm3=350L;350L ;
故答案为:8500;350。高级单位向低级单位换算,高级单位乘进率;1立方分米=1升。
22.27立方厘米;54平方厘米
解:棱长:36÷12=3(cm);体积:3×3×3=27(立方厘米);表面积:3×3×6=54(平方厘米)。
故答案为:27立方厘米;54平方厘米。
用正方体的棱长和除以12求出棱长,正方体体积=棱长×棱长×棱长,正方体表面积=棱长×棱长×6,根据公式计算即可。
23.318;378
解:长方体表面积:(9×7+9×6+7×6)×2
=(63+54+42)×2
=159×2
=318(cm2);
体积:9×7×6
=63×6
=378(cm3);
故答案为:318;378。
根据长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高,代入数值计算即可。
24.;
解:1÷5=;
4÷5=(升);
故答案为:;。
把整体平均分成几份,每一份就是整体的几分之一;求每瓶水的质量,就用总质量除以瓶子个数;据此解答。
25.30
解:2×3×5
=6×5
=30
故答案为:30。
由题意可知,这个数是2、3、5的最小公倍数,三个质数的最小公倍数是它们的乘积;据此解答。
26.升;厘米;立方厘米;毫升
解:一桶色拉油的容积是5升;
一支铅笔的长约15厘米;
一块橡皮的体积约为6立方厘米;
一盒牛奶的体积约250毫升;
故答案为:升;厘米;立方厘米;毫升。
常用的容积单位有:升、毫升;常用的长度单位有毫米、厘米、分米、米……;常用的体积单位有:立方厘米、立方分米、立方米……;结合日常实际进行解答。
27.5.2;4;80
解:5200÷1000=5.2,所以5200dm3=5.2m3;
4.08dm3=4dm3+0.08dm3,4dm3=4L,0.08dm3=80mL,所以4.08dm3=4L80mL;
故答案为:5.2;4;80。
1立方米=1000立方分米;1立方分米=1升=1000毫升;据此进行单位换算。
28.4;8
解:表面积扩大为原来的4倍,体积扩大为原来的23=8倍。
故答案为:4;8。
长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,当一个长方体的长、宽、高都扩大为原来的2倍时,现在长方体的表面积=(长×2×宽×2+长×2×高×2+宽×2×高×2)×2=(长×宽×4+长×高×4+宽×高×4)×2=(长×宽+长×高+宽×高)×2×4=原来长方体的表面积×4,现在长方体的体积=长×2×宽×2×高×2=长×宽×高×8=原来长方体的体积×8。
29.
- +
解:-;
+
故答案为:-;+。
异分母分数相加减,先通风成同分母分数,再进行相加减。
30.9800;9800;32;0.021
解:9.8×1000=9800(毫升)=9800立方厘米,所以,9.8升=9800毫升=9800立方厘米;
3.2×10=32(分米),3.2米=32分米;
2.1÷100=0.021(平方米),2.1平方分米=0.021平方米;
故答案为:9800;9800;32;0.021。
1升=1000毫升=1000立方厘米;1米=10分米;1平方米=100平方分米;大单位换算成小单位要乘进率,小单位换算成大单位要除以进率;据此解答。
31.立方米;毫升;平方米;米
解:集装箱的体积约是40立方米;
一瓶纯净水约500毫升;
操场的面积约是2000平方米;
游泳池水深2米。
故答案为:立方米;毫升;平方米;米。
常见的体积单位有:立方厘米、立方分米、立方米等;常见的容积单位有:毫升、升;常见的面积单位有:平方厘米、平方米、公顷、平方千米等;常见的长度单位有:厘米、米、千米等。
集装箱的体积非常大,应选用大的体积单位;一瓶纯净水通常用毫升或升作单位,如果前面的数字比较大,则选用较小的毫升做单位,反之,则选用升作单位;操场的面积不算特别大,应选用一般大的面积单位;游泳池的水深一般和成年人身高差不多,应选用长度单位。
32.16;10;0.8
解:20×=16;8÷=10;=4÷5=0.8。
故答案为:16;10;0.8。
分子=分母×分数值;除数=被除数÷商;分数化小数:用分子除以分母,商写成小数的形式。
33.;;8;;;2;80
解:53÷60=,所以53分=时;
13÷1000=,所以13克=千克;
8÷1=8,所以8 dm3= 8L ;
360÷100=,所以 360dm2 = m2 ;
7100÷1000=,所以 7100dm3= m3 ;
2.08×1000=2080,2080÷1000=2(m3)……80( dm3 ),所以 2.08m3= 2 m3 80 dm3
故答案为:;;8;;;2;80。
1时=60分,1千克=1000克,1升=1立方分米,1立方米=1000立方分米,把高级单位换算成低级单位要乘以进率,把低级单位换算成高级单位要除以进率。
34.54
解:36÷12=3(dm),
3×3×6
=9×6
=54(dm2)
故答案为:54。
正方体的棱长=正方体的棱长之和÷12,正方体的表面积=棱长×棱长×6。
35.8
解: 若是假分数,m≤8;
若是真分数,m>7;
则m一定是8。
故答案为:8。
分子比分母小的分数叫做真分数;分子比分母大或分子和分母相等的分数叫做假分数。
36.;13;3
解:=;的分数单位是,它里面有13个这样的分数单位;
最小的合数是4,4=,-=,再添上3个这样的分数单位就是最小的合数。
故答案为:;13;3。
一个分数的分数单位就是分母分之一,它有分子个这样的分数单位。
37.72
解:26×2+5×4
=52+20
=72(厘米)
至少要72cm铁丝。
故答案为:72。
底面周长×2=4个长4个宽的和,高×4=4个高的和,4个长4个宽的和+4个高的和=长方体的棱长和。
38.12;20;0.75
解:==12÷16;=;=3÷4=0.75。
故答案为:12;20;0.75。
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变;
分数与除法的关系:被除数÷除数=商写成分数的形式,分子是被除数,分母是除数;
分数化小数:用分子除以分母,商写成小数的形式。
39.90;78
解:6×5×3
=30×3
=90(立方厘米)
90-12=78(个)。
故答案为:90;78。
它的容积=长×宽×高;其中,长、宽、高分别是长边、宽边、高边小正方体的个数;李老师拿出小正方体的个数=总个数-现在有的个数。
40.2;7
解:8-6=2(个)
12-5=7(根)。
故答案为:2;7。
正方体有12条棱、8个顶点,还需要磁力珠的个数=8-现有的个数,还需要磁力棒的根数=12-现有的根数。
41.1080;886;0.886;0.0027;9;870
解:10.8 ×100=1080(dm2),所以10.8m2= 1080dm2;
886mL=886cm3,886÷1000=0.886(dm3),所以886cm3=0.886dm3
2700÷1000000=0.0027m3,所以2700cm3=0.0027m3
9L+0.87L=9L+0.87×1000mL=9L870mL,所以9.87L=9L870mL;
故答案为:1080;886;0.886;0.0027;9;870。
根据1m2=100dm2,1mL = 1cm3,1L=1000mL,1m3=1000000cm3,高级单位的数×进率=低级单位的数,低级单位的数÷进率=高级单位的数。
42.24;8
解:24÷12=2(dm);
表面积:2×2×6=4×6=24(dm2)
体积:2×2×2=4×2=8(dm3)
故答案为:24;8。
正方体的棱长=总棱长÷12;正方体表面积=棱长×棱长×6;正方体体积=棱长×棱长5棱长。
43.5;4
解:分母为5的假分数有:
分母为5的最小假分数为:。
所以当a=5时,这个分数可以 成最小假分数 。
分母为5的真分数有:
分母为5的最小真分数为:
当a=4时,这个分数是最大的真分数。
故答案为:5;4。
分子比分母小的分数叫做真分数。分子比分母大或者分子和分母相等的分数,叫做假分数。据此解即可。
44.30.5;7850;4050;5;600
解:3050÷100=30.5,所以3050平方厘米=30.5平方分米
7.85×1000=7850,所以7.85立方分米=7850立方厘米
4×1000=4000,所以4立方米50立方分米=4050立方分米
5000÷1000=5,所以5600毫升=5升600毫升
故答案为:30.5;7850;4050;5;600。
1平方分米=100平方厘米,1立方分米=1000立方厘米,1立方米=1000立方分米,1升=1000毫升;把高级单位换算成低级单位要乘进率,把低级单位换算成高级单位要除以进率。
45.0.125;0.45;2.8;
解:=1÷8=0.125;
9÷20=0.45;
=2+4÷5=2+0.8=2.8;
1.5=
故答案为:0.125;0.45;2.8;。
分数化小数,用分子除以分母,除不尽的要要求用四舍五入法保留对应的数位;
小数化分数 ,整数保持部分不变,用小数部分的全部数乘以最后一位小数的计数单位,再将所得分数化为最简分数。
46.11;99
解:4+3+4=7+4=11(个);
3×3×11=9×11=99(cm2)
故答案为:11;99。
看图,数一数,发现有11个面露在外面,并且每个面都是边长为3cm的正方形。正方形的面积=边长×边长。
47.;6
解:+=(米)
×9=6。
故答案为:;6。
求比一个数多几的数是多少,用加法计算;
求几个相同加数的和的简便运算叫做乘法。
48.9;36;27
解:每个面的面积:54÷6=9(dm2);
9=3×3,所以正方体的棱长是3dm;
棱长之和是:3×12=36(dm);
体积是:3×3×3=27(dm3);
故答案为:9;36;27。
正方体表面积=底面积×6,所以它每个面的面积=表面积÷6;正方体的底面积=棱长×棱长,据此可以计算出正方体的棱长,正方体有12条相等的棱,所以正方体棱长和=棱长×12;正方体体积=棱长×棱长×棱长;据此解答。
49.;
解: ×6= ;
× =
故答案为:;。
求一个数的几倍是多少,用乘法;
求一个数的几分之几是多少,用乘法。
50.小;5
解:一个容器壁再薄也有厚度, 所以一个容器的容积一定比它的体积小 ;
1升=1000毫升,1000÷200=5(杯)
故答案为:小;5。
物体的体积是指物体所占空间的大小;物体的容积是指物体所能容纳物质的多少;它们的意义不同,在测量数据时,计算体积需从物体的外面测量;而计算容积需从物体的里面测量,所以物体容积小于物体体积;1L=1000mL,用1000除以200即可求出可以倒的杯子数。
期中考试真题分类汇编 03 填空题
一、填空题
1.(2024五下·湛江期中)一个长方体的长是15 dm ,宽是5dm ,高是长的,这个长方体的体积是 dm,表面积是 dm。
2.(2024五下·威县期中)张叔叔承包了一片山地,他准备用这片山地的 种农作物, 种果树。如果农作物的 是玉米, 玉米地占整块地的 , 如果果树的 是枣树, 枣树占整块地的 。
3.(2024五下·高邮期中) 若a=b+1(a、b都是大于0的自然数),则a和b的最大公因数是 ,最小公倍数是 。
4.(2022五下·巧家期中) = = =45÷ = (填带分数)= (填小数)。
5.(2024五下·薛城期中)
(1)把一条1米长的彩带平均分成5份,每份长 米。
(2)把一条2米长的彩带平均分成5份,每份是 个 米,是 米。
6.(2024五下·德州期中)a=2×5×m,b=3×5×m(m是不为0的自然数),如果a和b的最大公因数是65,那么a和b的最小公倍数是 。
7.(2024五下·章贡期中)已知A=2x3x3x5,B=2x2x5,C=3x3x5,那么A,B,C的最大公因数是 ,最小公倍数是 。
8.(2024五下·霞山期中)正方体的棱长总和是48厘米,它的棱长是 厘米。
9.(2024五下·墨玉期中) 2.5L= mL 12dm3= cm3
3.85m3= dm3 785mL= cm3= dm3
10.(2023五下·阳山期中)正方体的棱长扩大到原来的3倍,棱长总和扩大到原来的 倍,表面积扩大到原来的 倍,体积扩大到原来的 倍。
11.(2024五下·龙岗期中)2÷ =× =+ =0.25=- 。
12.(2024五下·安阳期中)如图,将一个正方体的棱长从2cm增加到4cm,它的棱长总和扩大到原来的 倍,表面积扩大到原来的 倍,体积扩大到原来的 倍。
13.(2024五下·万载期中)一根6m长的方钢,把它横截成3段时,表面积增加120cm2,原来方钢的体积是 。
14.(2024五下·兰溪期中)320cm2= m2 6.25L= mL
5.2m= m cm 60mL= L
15.(2024五下·隆回期中)a÷b=8,那么a和b的最大公因数是 ,最小公倍数是 。
16.(2024五下·汉川期中)修路队要用216立方米的沙子铺路,铺的路宽2米,要铺3厘米厚,这些沙子一共能铺 长的路。
17.(2024五下·汉川期中)在横线上填上合适的单位名称.。
一个苹果的体积约130 一大瓶可乐的容积是2
18.(2024五下·汉川期中)下图是一个正方体表面的展开图,每面都标有数字。在正方体中,数字“3”对面的数字是 ,相交于同一个顶点的三个面上的数字之和最小是 。
19.(2024五下·苍南期中)如图是一个长方体展开图。
(1)如果长方形B在下面,那么长方形 在上面;如果长方形C在前面,那么长方形 在后面。
(2)根据图中的数据(单位:dm),这个长方体的体积是 dm3。
20.(2024五下·邯郸期中)与 互为倒数,最小合数的倒数是 。
21.(2024五下·电白期中)8.5m3= dm3 L
22.(2024五下·蕲春期中)一个正方体的棱长和是36cm,它的体积是 ,表面积是 .
23.(2024五下·陆丰期中)一个长方体相交于一个顶点的三条棱分别长9cm、7cm和6cm,它的表面积是 cm2,体积是 cm3。
24.(2024五下·陆丰期中)把4L水平均装在5个瓶子里,每个瓶子里的水占这些水的 ,每瓶水有 升。
25.(2024五下·陆丰期中)一个三位数既有因数2,又有因数3,同时又是5的倍数,这个数最小是 。
26.(2024五下·陆丰期中)填上合适的单位。
一桶色拉油的容积是5 , 一支铅笔的长约15
一块橡皮的体积约为6 一盒牛奶的体积约250
27.(2024五下·陆丰期中)5200dm3= m3 4.08dm3= L mL。
28.(2024五下·陆丰期中)一个长方体的长、宽、高都扩大为原来的2倍,则表面积扩大为原来的 倍,体积扩大为原来的 倍。
29.(2024五下·电白期中)看图填一填。
- +
30.(2024五下·广州期中)9.8升= 毫升= 立方厘米
3.2米= 分米
2.1平方分米= 平方米
31.(2024五下·广州期中)在横线里填入合适的单位。
集装箱的体积约是40 ,一瓶纯净水约500 ,
操场的面积约是2000 ,游泳池水深2 。
32.(2024五下·桑植期中) = =8÷ = (填小数)。
33.(2024五下·茂名期中)在横线上填合适的分数。
53分= 时 13克= 千克
8dm3= L 360dm2= m2
7100dm3= m3 2.08m3= m3 dm3
34.(2024五下·茂名期中)一个正方体的棱长之和是36dm,这个正方体的表面积是
35.(2024五下·汝城期中) 若是假分数,是真分数, 则m一定是 。
36.(2024五下·汝城期中)的分数单位是 ,它里面有 个这样的分数单位,再添上 个这样的分数单位就是最小的合数。
37.(2024五下·汝城期中) 做一个底面周长26cm,高5cm的长方体框架,至少要 cm铁丝。
38.(2024五下·汝城期中) ÷16= = (填小数)。
39.(2024五下·临平期中)一个透明的塑料盒里装满了体积为1cm3的小正方体。它的容积是 cm3,李老师从盒里拿出一些准备在数学课上用,还剩下一部分(如图),李老师拿出了 个小正方体。
40.(2024五下·临平期中)要搭成一个正方体框架,还需要 个磁力珠和 根磁力棒。
41.(2024五下·辰溪期中)10.8m2= dm2 886mL= cm3= dm3
2700 cm3= m3 9.87L= L mL
42.(2024五下·电白期中)用一根24dm长的铁丝焊成一个正方体框架,这个正方体的表面积是 ,体积是
。
43.(2024五下·怀化期中) 在中,当a= 时,这个分数可以化成最小假分数;当a= 时,它是最大的真分数。
44.(2024五下·汝城期中)3050cm2= dm2 cm3
dm3 5600mL= L mL
45.(2024五下·电白期中)在横线上填上合适的小数或分数。
= 1.5=
46.(2024五下·电白期中)把5个棱长为3cm的正方体木块放在墙角处(如下图)有 个面露在外面,露在外面的面积是 cm2。
47.(2024五下·邯郸期中)比米长米是 米,9个时的和是 时。
48.(2024五下·陆丰期中)一个正方体的表面积是54dm2,它每个面的面积是 dm2,这个正方体的棱长之和是 dm,它的体积是 dm3。
49.(2024五下·电白期中)kg的6倍是 ,的是 。
50.(2024五下·茂名期中)一个容器的容积一定比它的体积 (填“大、小、无法比较”)。把1升的水倒入容量为200毫升的纸杯中,可倒 杯。
答案解析部分
1.225;270
解:高:15×=3(dm);
体积:15×5×3=225(dm3);
表面积:(15×5+15×3+5×3)×2
=(75+45+15)×2
=135×2
=270(dm2)
故答案为:225;270。
长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高,先求出高,然后分别求出体积和表面积即可。
2.;
解:×=
×=。
故答案为:;。
玉米地占整块地的分率=农作物占的分率×玉米占的分率,枣树占整块地的分率=果树占的分率×枣树占的分率。
3.1;ab
解:a和b的最大公因数是1,最小公倍数是ab;
故答案为:1;ab。
相邻自然数的最大公因数恒为1,最小公倍数为两数之积,据此求解。
4.25;24;36;;1.25
解:20×=25;30÷=24;45÷=36;=;=5÷4=1.25。
故答案为:25;24;36;;1.25。
分子=分母×分数值;分母=分子×分数值;除数=被除数÷商;分数化小数:用分子除以分母,商写成小数的形式。
5.(1)
(2)2; ;
解:(1)1÷5=(米);
(2)把一条2米长的彩带平均分成5份,每份是2个米,是米。
故答案为:;2;;。
(1)求每份的长度,用总长度除以份数即可解答;(2)2米里面有2个1米,平均分成的份数相同,那么,2米平均分成5份,每份的长度就是2个第一小题中每份长度。据此解答。
6.390
解:如果a=2×5×m,b=3×5×m(m是不为0的自然数),则a和b的最大公因数是5×m,
5×m=65
5×m÷5=65÷5
m=13
a=2×5×13;
b=3×5×13;
a和b的最小公倍数是:5×13×2×3=390
故答案为:390。
用分解质因数的方法求两个数的最大公因数,先把每个数分别分解质因数,再把两个数中的全部公有质因数提取出来连乘,所得的积就是这两个数的最大公因数;
用分解质因数的方法求两个数的最小公倍数,先把每个数分别分解质因数,把这两个数公有的质因数和各自独有的质因数相乘,它们的乘积就是这两个数的最小公倍数,据此解答。
7.5;180
解:A=2×3×3×5=90
B=2×2×5=20
C=3×3×5=45
A,B,C的最大公因数是5,最小公倍数是5×2×3×3×2=180。
故答案为:5;180。
先求出A=90,B=20,C=45,然后用短除法求出A,B,C的最大公因数、最小公倍数。
8.4
解:48÷12=4(厘米)。
故答案为:4。
正方体的棱长=正方体的棱长和÷12。
9.2500;12000;3850;785;0.785
解:2.5×1000=2500,所以 2.5升=2500毫升
12×1000=12000,所以12立方分米=12000立方厘米
3.85×1000=3850,所以3.85立方米=3850立方分米
785÷1000=0.785,所以 785毫升=785立方厘米=0.785立方分米
故答案为:2500;12000;3850;785;0.785。
1升=1000毫升,1立方分米=1000立方厘米,1立方米=1000立方分米,1毫升=1立方厘米,1立方分米=1000立方厘米;把高级单位换算成低级单位要乘进率,把低级单位换算成高级单位要除以进率。
10.3;9;27
解:3×1=3
3×3=9
3×3×3=27。
故答案为:3;9;27。
正方体的棱长和=棱长×12;正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长。正方体的棱长扩大到原来的3倍,棱长总和扩大到原来的3倍,表面积扩大到原来的9倍,体积扩大到原来的27倍。
11.8;;;
2÷0.25=8;
0.25÷=;
0.25-=0
-0.25=。
故答案为:8;;;。
除数=被除数÷商;一个因数=积÷另一个因数;一个加数=和-另一个加数;减数=被减数-差。
12.2;4;8
解:4÷2=2,棱长扩大到原来的2倍,
=2×2=4,=2×2×2=8,
它的棱长总和扩大到原来的2倍,表面积扩大到原来的4倍,体积扩大到原来的8倍。
故答案为:2;4;8。
正方体的棱长扩大到原来的n倍,棱长总和扩大到原来的n倍,表面积扩大到原来的n的平方倍,体积扩大到原来的n的立方倍。
13.18000立方厘米
解:6米=600厘米
120÷4×600
=30×600
=18000(立方厘米)。
故答案为:18000立方厘米。
原来方钢的体积=底面积×方钢的长,其中,底面积=增加的表面积÷增加面的个数。
14.0.032;6250;5;20;0.06
解:320÷10000=0.032(平方米),所以320平方厘米=0.032平方米;
6.25×1000=6250(毫升),所以6.25升=6250毫升;
(5.2-5)×100
=0.2×100
=20(厘米),所以5.2米=5米20厘米;
60÷1000=0.06(升),所以60毫升=0.06升。
故答案为:0.032;6250;5;20;0.06。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
15.b;a
解:a÷b=8,可知a和b是倍数关系,所以a和b的最大公因数是b,最小公倍数是a。
故答案为:b;a。
两数是倍数关系,最大公因数是较小数,最小公倍数是较大数。
16.3600
解:3厘米=0.03米
216÷(2×0.03)
=216÷0.06
=3600(米)。
故答案为:3600。
先单位换算3厘米=0.03米,这些沙子一共能铺路的长度=沙子的体积÷(要修路的宽×厚度)。
17.立方厘米;升
解:一个苹果的体积约130立方厘米;
一大瓶可乐的容积是2升。
故答案为:立方厘米;升。
根据实际生活经验以及题干中的具体数据来进行填空。
18.2;7
解:数字“3”对面的数字是2,数字1对面的数字是5,数字4对面的数字是6。
相交于同一个顶点的三个面上的数字之和最小是: 1、2、4相交于一个顶点,和是1+2+4=7。
故答案为:2;7。
正方体展开图的规律:中间四个成一行,两边各一无规矩;二三紧连错一个,三一相连一随意;两两相连各错一,三个两排一对齐;一条线上不过四,田七和凹要放弃;相间之端是对面,间二拐角面相邻。
相交于同一个顶点的三个面上的数字之和最小,即是找出两两相邻的三个面上的数字最小的面,即1、2、4,计算即可。
19.(1)E;F
(2)24
解:(1)如果长方形B在下面,那么长方形E在上面;如果长方形C在前面,那么长方形F在后面;
(2)4×3×2=24(立方分米)。
故答案为:(1)E;F;(2)24。
(1)长方体相对的面不相邻,则B和E相对,C和F相对,A和D相对;
(2)长方体的体积=长×宽×高。
20.;
解:1÷=
1÷4=。
故答案为:;。
最小的合数是4,求一个数0除外的倒数=1÷这个数。
21.8500;350
解:8.5×1000=8500dm3, 8.5m3=8500dm3 ;
dm3=350L;350L ;
故答案为:8500;350。高级单位向低级单位换算,高级单位乘进率;1立方分米=1升。
22.27立方厘米;54平方厘米
解:棱长:36÷12=3(cm);体积:3×3×3=27(立方厘米);表面积:3×3×6=54(平方厘米)。
故答案为:27立方厘米;54平方厘米。
用正方体的棱长和除以12求出棱长,正方体体积=棱长×棱长×棱长,正方体表面积=棱长×棱长×6,根据公式计算即可。
23.318;378
解:长方体表面积:(9×7+9×6+7×6)×2
=(63+54+42)×2
=159×2
=318(cm2);
体积:9×7×6
=63×6
=378(cm3);
故答案为:318;378。
根据长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高,代入数值计算即可。
24.;
解:1÷5=;
4÷5=(升);
故答案为:;。
把整体平均分成几份,每一份就是整体的几分之一;求每瓶水的质量,就用总质量除以瓶子个数;据此解答。
25.30
解:2×3×5
=6×5
=30
故答案为:30。
由题意可知,这个数是2、3、5的最小公倍数,三个质数的最小公倍数是它们的乘积;据此解答。
26.升;厘米;立方厘米;毫升
解:一桶色拉油的容积是5升;
一支铅笔的长约15厘米;
一块橡皮的体积约为6立方厘米;
一盒牛奶的体积约250毫升;
故答案为:升;厘米;立方厘米;毫升。
常用的容积单位有:升、毫升;常用的长度单位有毫米、厘米、分米、米……;常用的体积单位有:立方厘米、立方分米、立方米……;结合日常实际进行解答。
27.5.2;4;80
解:5200÷1000=5.2,所以5200dm3=5.2m3;
4.08dm3=4dm3+0.08dm3,4dm3=4L,0.08dm3=80mL,所以4.08dm3=4L80mL;
故答案为:5.2;4;80。
1立方米=1000立方分米;1立方分米=1升=1000毫升;据此进行单位换算。
28.4;8
解:表面积扩大为原来的4倍,体积扩大为原来的23=8倍。
故答案为:4;8。
长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,当一个长方体的长、宽、高都扩大为原来的2倍时,现在长方体的表面积=(长×2×宽×2+长×2×高×2+宽×2×高×2)×2=(长×宽×4+长×高×4+宽×高×4)×2=(长×宽+长×高+宽×高)×2×4=原来长方体的表面积×4,现在长方体的体积=长×2×宽×2×高×2=长×宽×高×8=原来长方体的体积×8。
29.
- +
解:-;
+
故答案为:-;+。
异分母分数相加减,先通风成同分母分数,再进行相加减。
30.9800;9800;32;0.021
解:9.8×1000=9800(毫升)=9800立方厘米,所以,9.8升=9800毫升=9800立方厘米;
3.2×10=32(分米),3.2米=32分米;
2.1÷100=0.021(平方米),2.1平方分米=0.021平方米;
故答案为:9800;9800;32;0.021。
1升=1000毫升=1000立方厘米;1米=10分米;1平方米=100平方分米;大单位换算成小单位要乘进率,小单位换算成大单位要除以进率;据此解答。
31.立方米;毫升;平方米;米
解:集装箱的体积约是40立方米;
一瓶纯净水约500毫升;
操场的面积约是2000平方米;
游泳池水深2米。
故答案为:立方米;毫升;平方米;米。
常见的体积单位有:立方厘米、立方分米、立方米等;常见的容积单位有:毫升、升;常见的面积单位有:平方厘米、平方米、公顷、平方千米等;常见的长度单位有:厘米、米、千米等。
集装箱的体积非常大,应选用大的体积单位;一瓶纯净水通常用毫升或升作单位,如果前面的数字比较大,则选用较小的毫升做单位,反之,则选用升作单位;操场的面积不算特别大,应选用一般大的面积单位;游泳池的水深一般和成年人身高差不多,应选用长度单位。
32.16;10;0.8
解:20×=16;8÷=10;=4÷5=0.8。
故答案为:16;10;0.8。
分子=分母×分数值;除数=被除数÷商;分数化小数:用分子除以分母,商写成小数的形式。
33.;;8;;;2;80
解:53÷60=,所以53分=时;
13÷1000=,所以13克=千克;
8÷1=8,所以8 dm3= 8L ;
360÷100=,所以 360dm2 = m2 ;
7100÷1000=,所以 7100dm3= m3 ;
2.08×1000=2080,2080÷1000=2(m3)……80( dm3 ),所以 2.08m3= 2 m3 80 dm3
故答案为:;;8;;;2;80。
1时=60分,1千克=1000克,1升=1立方分米,1立方米=1000立方分米,把高级单位换算成低级单位要乘以进率,把低级单位换算成高级单位要除以进率。
34.54
解:36÷12=3(dm),
3×3×6
=9×6
=54(dm2)
故答案为:54。
正方体的棱长=正方体的棱长之和÷12,正方体的表面积=棱长×棱长×6。
35.8
解: 若是假分数,m≤8;
若是真分数,m>7;
则m一定是8。
故答案为:8。
分子比分母小的分数叫做真分数;分子比分母大或分子和分母相等的分数叫做假分数。
36.;13;3
解:=;的分数单位是,它里面有13个这样的分数单位;
最小的合数是4,4=,-=,再添上3个这样的分数单位就是最小的合数。
故答案为:;13;3。
一个分数的分数单位就是分母分之一,它有分子个这样的分数单位。
37.72
解:26×2+5×4
=52+20
=72(厘米)
至少要72cm铁丝。
故答案为:72。
底面周长×2=4个长4个宽的和,高×4=4个高的和,4个长4个宽的和+4个高的和=长方体的棱长和。
38.12;20;0.75
解:==12÷16;=;=3÷4=0.75。
故答案为:12;20;0.75。
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变;
分数与除法的关系:被除数÷除数=商写成分数的形式,分子是被除数,分母是除数;
分数化小数:用分子除以分母,商写成小数的形式。
39.90;78
解:6×5×3
=30×3
=90(立方厘米)
90-12=78(个)。
故答案为:90;78。
它的容积=长×宽×高;其中,长、宽、高分别是长边、宽边、高边小正方体的个数;李老师拿出小正方体的个数=总个数-现在有的个数。
40.2;7
解:8-6=2(个)
12-5=7(根)。
故答案为:2;7。
正方体有12条棱、8个顶点,还需要磁力珠的个数=8-现有的个数,还需要磁力棒的根数=12-现有的根数。
41.1080;886;0.886;0.0027;9;870
解:10.8 ×100=1080(dm2),所以10.8m2= 1080dm2;
886mL=886cm3,886÷1000=0.886(dm3),所以886cm3=0.886dm3
2700÷1000000=0.0027m3,所以2700cm3=0.0027m3
9L+0.87L=9L+0.87×1000mL=9L870mL,所以9.87L=9L870mL;
故答案为:1080;886;0.886;0.0027;9;870。
根据1m2=100dm2,1mL = 1cm3,1L=1000mL,1m3=1000000cm3,高级单位的数×进率=低级单位的数,低级单位的数÷进率=高级单位的数。
42.24;8
解:24÷12=2(dm);
表面积:2×2×6=4×6=24(dm2)
体积:2×2×2=4×2=8(dm3)
故答案为:24;8。
正方体的棱长=总棱长÷12;正方体表面积=棱长×棱长×6;正方体体积=棱长×棱长5棱长。
43.5;4
解:分母为5的假分数有:
分母为5的最小假分数为:。
所以当a=5时,这个分数可以 成最小假分数 。
分母为5的真分数有:
分母为5的最小真分数为:
当a=4时,这个分数是最大的真分数。
故答案为:5;4。
分子比分母小的分数叫做真分数。分子比分母大或者分子和分母相等的分数,叫做假分数。据此解即可。
44.30.5;7850;4050;5;600
解:3050÷100=30.5,所以3050平方厘米=30.5平方分米
7.85×1000=7850,所以7.85立方分米=7850立方厘米
4×1000=4000,所以4立方米50立方分米=4050立方分米
5000÷1000=5,所以5600毫升=5升600毫升
故答案为:30.5;7850;4050;5;600。
1平方分米=100平方厘米,1立方分米=1000立方厘米,1立方米=1000立方分米,1升=1000毫升;把高级单位换算成低级单位要乘进率,把低级单位换算成高级单位要除以进率。
45.0.125;0.45;2.8;
解:=1÷8=0.125;
9÷20=0.45;
=2+4÷5=2+0.8=2.8;
1.5=
故答案为:0.125;0.45;2.8;。
分数化小数,用分子除以分母,除不尽的要要求用四舍五入法保留对应的数位;
小数化分数 ,整数保持部分不变,用小数部分的全部数乘以最后一位小数的计数单位,再将所得分数化为最简分数。
46.11;99
解:4+3+4=7+4=11(个);
3×3×11=9×11=99(cm2)
故答案为:11;99。
看图,数一数,发现有11个面露在外面,并且每个面都是边长为3cm的正方形。正方形的面积=边长×边长。
47.;6
解:+=(米)
×9=6。
故答案为:;6。
求比一个数多几的数是多少,用加法计算;
求几个相同加数的和的简便运算叫做乘法。
48.9;36;27
解:每个面的面积:54÷6=9(dm2);
9=3×3,所以正方体的棱长是3dm;
棱长之和是:3×12=36(dm);
体积是:3×3×3=27(dm3);
故答案为:9;36;27。
正方体表面积=底面积×6,所以它每个面的面积=表面积÷6;正方体的底面积=棱长×棱长,据此可以计算出正方体的棱长,正方体有12条相等的棱,所以正方体棱长和=棱长×12;正方体体积=棱长×棱长×棱长;据此解答。
49.;
解: ×6= ;
× =
故答案为:;。
求一个数的几倍是多少,用乘法;
求一个数的几分之几是多少,用乘法。
50.小;5
解:一个容器壁再薄也有厚度, 所以一个容器的容积一定比它的体积小 ;
1升=1000毫升,1000÷200=5(杯)
故答案为:小;5。
物体的体积是指物体所占空间的大小;物体的容积是指物体所能容纳物质的多少;它们的意义不同,在测量数据时,计算体积需从物体的外面测量;而计算容积需从物体的里面测量,所以物体容积小于物体体积;1L=1000mL,用1000除以200即可求出可以倒的杯子数。
同课章节目录
