2025年九年级中考数学三轮冲刺训练高频考点突破圆的切线的证明(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺训练高频考点突破圆的切线的证明(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-04 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺训练高频考点突破圆的切线的证明
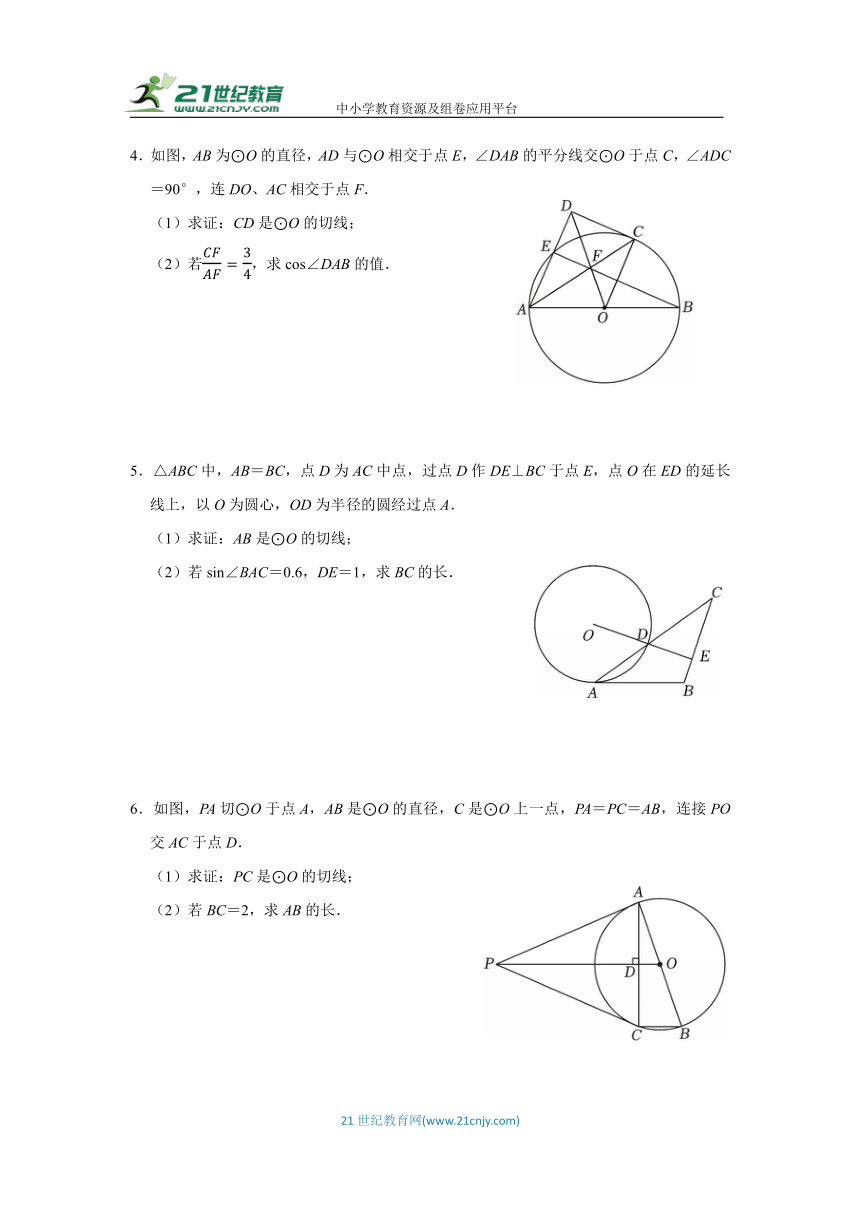
1.如图,在Rt△ABC中,E为斜边AB上的一点,经过点E的⊙O与AC交于点D,连接DO,DE.若ED∥BC,∠CDO=∠B.
(1)求证:AB为⊙O的切线;
(2)若OD=BE=5,DE=6,求AC的长.
2.如图,BE是⊙O的直径,A,D是⊙O上的两点,延长BE至点C,连接AC,∠EAC=∠ABC.
(1)求证:CA是⊙O的切线;
(2),BC=10,求⊙O的半径.
3.如图,在Rt△ABC中,∠C=90°,点O在AC边上,以OA为半径的半圆O交AB于点D,交AC于点E,在BC边上取一点F,连接FD,使得DF=BF.
(1)求证:DF为半圆O的切线;
(2)若AC=6,BC=4,CF=1,求半圆O的半径长.
4.如图,AB为⊙O的直径,AD与⊙O相交于点E,∠DAB的平分线交⊙O于点C,∠ADC=90°,连DO、AC相交于点F.
(1)求证:CD是⊙O的切线;
(2)若,求cos∠DAB的值.
5.△ABC中,AB=BC,点D为AC中点,过点D作DE⊥BC于点E,点O在ED的延长线上,以O为圆心,OD为半径的圆经过点A.
(1)求证:AB是⊙O的切线;
(2)若sin∠BAC=0.6,DE=1,求BC的长.
6.如图,PA切⊙O于点A,AB是⊙O的直径,C是⊙O上一点,PA=PC=AB,连接PO交AC于点D.
(1)求证:PC是⊙O的切线;
(2)若BC=2,求AB的长.
7.如图,AB为⊙O的直径,过圆上一点D作⊙O的切线CD交BA的延长线于点C,过点O作OE∥AD交CD于点E,连接BE.
(1)求证:直线BE是⊙O的切线;
(2)若CA=2,CD=4,求DE的长.
8.如图,AB为⊙O的直径,点C在⊙O上,∠ACB的平分线CD交⊙O于点D,过点D作DE∥AB,交CB的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AC=8,BC=6,求AD及BE的长.
9.如图,△ABC中,以AB为直径的⊙O交BC于点E,AE平分∠BAC,过点E作ED⊥AC于点D,延长DE交AB的延长线于点P.
(1)求证:PE是⊙O的切线;
(2)若,BP=4,求CD的长.
10.如图,AB为⊙O的直径,C、F为⊙O上两点,且点C为弧BF的中点,过点C作AF的垂线,交AF的延长线于点E,交AB的延长线于点D.
(1)求证:DE是⊙O的切线;
(2)若AE=3,DE=4,求⊙O的半径的长.
11.如图,AB是⊙O的直径,PB⊥AB,过点B作BC⊥OP交⊙O于点C,垂足为D,连接PC并延长与BA的延长线交于点M.
(1)求证:PM是⊙O的切线;
(2)若OD=2,OP=18,求的值.
12.如图,AB是⊙O的直径,点D是⊙O上一点,过点A的切线与弦BD的延长线交于点C,过点D的直线交线段AC于点E,且DE=CE.
(1)求证:直线DE与⊙O相切;
(2)已知⊙O的半径是4,∠B=30°,求阴影部分的面积.
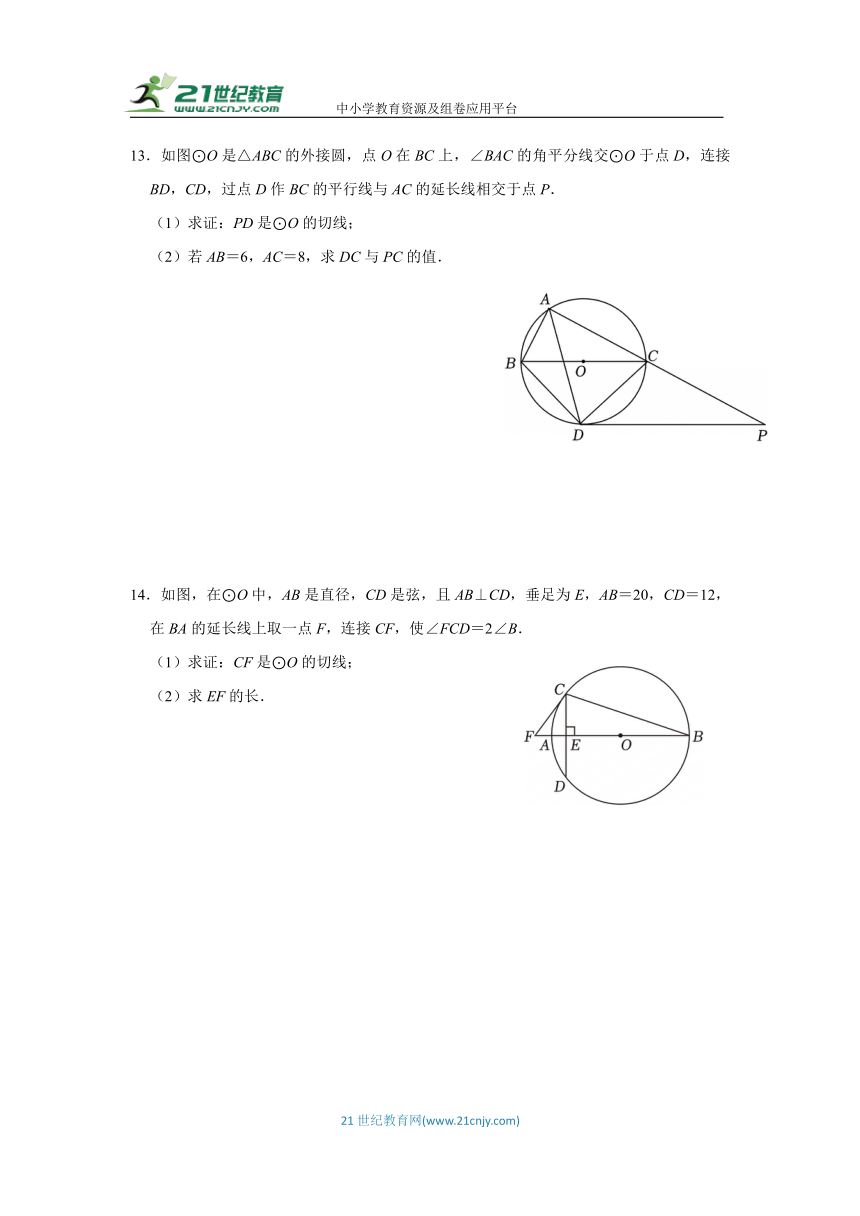
13.如图⊙O是△ABC的外接圆,点O在BC上,∠BAC的角平分线交⊙O于点D,连接BD,CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)若AB=6,AC=8,求DC与PC的值.
14.如图,在⊙O中,AB是直径,CD是弦,且AB⊥CD,垂足为E,AB=20,CD=12,在BA的延长线上取一点F,连接CF,使∠FCD=2∠B.
(1)求证:CF是⊙O的切线;
(2)求EF的长.
15.如图,点C在以AB为直径的⊙O上,点D在BA的延长线上,∠DCA=∠CBA.
(1)求证:DC是⊙O的切线;
(2)点G是半径OB上的点,过点G作OB的垂线与BC交于点F,与DC的延长线交于点E,若sinD,DA=FG=2,求CE的长.
16.如图,在Rt△ABC中,∠ACB=90°,点E在AC上,以CE为直径的⊙O经过AB上的点D,与OB交于点F,且BD=BC.
(1)求证:AB是⊙O的切线;
(2)若AD,AE=1,求的长.
参考答案
1.【解答】(1)证明:∵ED∥BC,∠C=90°,
∴∠AED=∠B,∠CDE=90°,
又∵∠CDO=∠B,
∴∠AED=∠CDO,
∵OD=OE,
∴∠OED=∠ODE,
∴∠AED+∠OED=∠CDO+∠ODE=90°,即∠AEO=90°,
又∵OE是半径;
∴AB为⊙O的切线;
(2)解:由(1)知∠GDE=90°,OD=BE=5,DE=6,如图,延长DC交⊙O于点G,连接OG,
∴EG是直径,即O、E、G三点共线,
∴EG=2OD=2×5=10,
在直角三角形DEG中,DE=6,
由勾股定理得:8,
∴,
又∵∠AEG=90°,
∴,
∴,
∵OD=OG,
∴∠G=∠CDO,
又∵∠CDO=∠B,
∴∠G=∠B,
∴,
在Rt△ABC中,.
2.【解答】(1)证明:连接OA,
∵OA=OB,
∴∠1=∠2,
∵∠1=∠3,
∴∠2=∠3,
∵BE是⊙O的直径,
∴∠BAE=∠2+∠OAE=90°,
∴∠3+∠OAE=90°,
∴∠OAC=90°,即OA⊥AC,
∵OA是半径,
∴CA是⊙O的切线;
(2)解:如图:
由题意可得:∠1=∠D,
∵∠BAE=90°,
∴,
∵∠1=∠3,∠C=∠C,
∴△CAE∽△CBA,
∴,
∴,
∴AC=6,,
∴,
∴.
3.【解答】(1)证明:连接OD,则OD=OA,
∴∠ODA=∠A,
∵DF=BF,
∴∠FDB=∠B,
∵∠C=90°,
∴∠ODA+∠FDB=∠A+∠B=90°,
∴∠ODF=180°﹣(∠ODA+∠FDB)=90°,
∵OD是⊙O的半径,且DF⊥OD,
∴DF是半圆O的切线.
(2)解:连接OF,设半圆O的半径长为r,
∵AC=6,BC=4,CF=1,
∴DF=BF=BC﹣CF=4﹣1=3,OC=AC﹣OA=6﹣r,
∵∠ODF=∠C=90°,
∴OD2+DF2=OC2+CF2=OF2,
∴r2+32=(6﹣r)2+12,解得r,
∴半圆O的半径长是.
4.【解答】(1)证明:∵AC平分∠DAB,
∴∠DAC=∠OAC,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠DAC=∠OCA,
∴OC∥AD,
∴∠ADC+∠OCD=180°,
∵∠ADC=90°,
∴∠OCD=90°,
∴半径OC⊥CD,
∴CD是⊙O的切线;
(2)过O作OH⊥AD于H,
由(1)知:OC∥AD,
∴△OCF∽△DAF,
∴OC:AD=CF:AF=3:4,
∴令OC=3x,AD=4x,
∴OA=OC=3x,
∵∠ADC=∠OCD=∠OHD=90°,
∴四边形DCOH是矩形,
∴DH=OC=3x,
∴AH=AD﹣DH=x,
∴cos∠DAB.
5.【解答】(1)证明:连接OA,如图,
∵AB=BC,
∴∠BAC=∠C,
∵DE⊥BC,
∴∠C+∠CDE=90°,
∵OA=OD,
∴∠OAD=∠ODA,
∵∠ODA=∠CDE,
∴∠OAD+∠BAC=∠C+∠CDE=90°,
∴AB是⊙O的切线;
(2)解:连接BD,如图,
∵AB=BC,点D为AC中点,
∴BD⊥AC,
∴∠CDE+∠BDE=∠CDE+∠C=90°,
∴∠BDE=∠C=∠BAC,
∵sin∠BAC=0.6,
∴sin∠BDE,
∴BE=0.6BD,
∵BD2﹣BE2=DE2,DE=1,
∴BD2﹣(0.6BD)2=1,
∴BD,
∴BC.
6.【解答】(1)证明:如图,连接OC,
∵PA是⊙O的切线,
∴PA⊥OA.
∴∠PAO=90°.
∵OC=OA,PC=PA,OP=OP.
∴△POC≌△POA(SSS).
∴∠PCO=∠PAO=90°.
∴PC⊥OC.
∴PC是⊙O的切线;
(2)∵∠PDA=∠ACB=90°,∠APD=∠BAC.
又∵PA=AB,
∴△PAD≌△ABC(AAS).
∴AD=BC=2,AC=2AD=4.
∴.
7.【解答】(1)证明:∵CD与⊙O相切于点D,
∴CD⊥OD,
∵OD=OA,
∴∠OAD=∠ODA,
∵OE∥AD交CD于点E,
∴∠BOE=∠OAD,∠DOE=∠ODA,
∴∠BOE=∠DOE,
∵OB=OD,OE=OE,
∴△BOE≌△DOE(SAS),
∴∠OBE=∠ODE=90°,
∵OB是⊙O的半径,且BE⊥OB,
∴直线BE是⊙O的切线.
(2)解:∵∠ODC=90°,
∴CD2+OD2=OC2,
∵CA=2,CD=4,OD=OA,
∴42+OA2=(2+OA)2,
∴OB=OD=OA=3,
∴BC=CA+OA+OB=2+3+3=8,
∵DE与⊙O相切于点D,BE与⊙O相切于点B,
∴DE=BE,
∵∠B=90°,
∴BC2+BE2=CE2,
∴82+DE2=(4+DE)2,
解得DE=6,
∴DE的长是6.
8.【解答】(1)证明:连接OD,
由角平分线定义可知∠ACD=∠BCD,
∴∠AOD=∠BOD,
∵AB为⊙O的直径,
∴,
∴OD⊥AB,
∵DE∥AB,
∴OD⊥DE,
∵OD为⊙O的半径,
∴直线DE是⊙O的切线;
(2)解:在Rt△ABC中,由勾股定理得,
由条件可知∠ACD=∠BCD,
∴,
∴,
∵DE∥AB,
∴∠BDE=∠ABD=∠ACD,
又四边形ACBD内接于⊙O,
∴∠CAD=∠DBE,
∴△BDE∽△ACD,
∴,
∴,
∴,
∴,.
9.【解答】(1)证明:如图,连接OE,
∵AE平分∠BAC,
∴∠OAE=∠DAE,
∵OE=OA,
∴∠OEA=∠OAE,
∴∠DAE=∠OEA,
∴OE∥AD,
∵ED⊥AC,
∴OE⊥PD,
∵OE是⊙O的半径,
∴PE是⊙O的切线;
(2)解:∵,BP=4,OB=OE,
∴,
∴OE=2,
∴AB=2OE=4,
∴AP=AB+BP=8,
在Rt△APD中,sin∠P,
∴ADAP,
∵AB为⊙O的直径,
∴∠AEB=90°=∠AEC,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵AE=AE,
∴△AEB≌△AEC(ASA),
∴AB=AC=4,
∴CD=AC﹣AD=4,
∴CD的长为.
10.【解答】(1)证明:连接OC,
∵点C为弧BF的中点,
∴弧BC=弧CF.
∴∠BAC=∠FAC,
∵OA=OC,
∴∠OCA=∠OAC.
∴∠OCA=∠FAC,
∴OC∥AE,
∵AE⊥DE,
∴OC⊥DE.
∴DE是⊙O的切线.
(2)解:由勾股定理得AD5,
∵∠OCD=∠AEC=90°,
∠D=∠D,
∴△OCD∽△AED,
∴,
即,
解得r,
∴⊙O的半径长为.
11.【解答】(1)证明:连接OC,
∵OC=OB,BC⊥OP,
∴∠COP=∠BOP,
∵OP=OP,
∴△PBO≌△PCO(SAS),
∴∠OCP=∠OBP,
∵PB⊥AB,
∴∠ABP=90°,
∴∠OCP=90°,
∴PM是⊙O的切线;
(2)解:连接AC,
∵∠OCP=∠CDO=90°,
∴∠OCD=∠CPO,
∴△OCD∽△OPC,
∴,
∴OC2=OD OP,
∵OD=2,OP=18,
∴OC=6,PD=OP﹣OD=16,
∴,
∴,
∴4,
∵∠ACM+∠ACO=∠OCD+∠ACO=90°,
∴∠ACM=∠OCD,
∴∠ACM=∠CPO,
∴AC∥OP,
∴△ACM∽△OPM,
∴,
∴.
12.【解答】(1)证明:连接OD、AD,则OD=OA,
∵AB是⊙O的直径,AC与⊙O相切于点A,
∴∠ADB=90°,AC⊥AB,
∴∠ADC=∠BAC=90°,
∴∠EDA=∠EDC=90°,∠EAD+∠C=90°,
∵DE=CE,
∴∠EDC=∠C,
∴∠EDA=∠EAD,
∵∠ODA=∠OAD,
∴∠ODE=∠ODA+∠EDA=∠OAD+∠EAD=∠BAC=90°,
∵OD是⊙O的半径,且DE⊥OD,
∴直线DE与⊙O相切.
(2)解:∵∠EDC=∠C,∠EDA=∠EAD,
∴CE=AE=DEAC,
∵⊙O的半径是4,∠B=30°,
∴OD=OA=OBAB=4,AB=8,∠AOD=2∠B=60°,
∴△AOD是等边三角形,
∴AD=OD=4,∠BAD=60°,
∴BD4,∠CAD=∠BAC﹣∠BAD=30°,
∴AC=2CD,
∵ADCD=4,
∴CD,
∵S△ABD4×48,S△ACD4,
∴S△AODS△ABD=4,S△AEDS△ACD,
∵S扇形AOD,
∴S阴影=S△AOD+S△AED﹣S扇形AOD=4,
∴阴影部分的面积为.
13.【解答】(1)证明:如图1,连接OD,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴,
∴∠BOD=∠COD=90°,
∵BC∥PD,
∴∠ODP=∠BOD=90°,
∴OD⊥PD,
∵OD是半径,
∴PD是⊙O的切线;
(2)解:∵BC是⊙O的直径,
∴∠BAC=∠BDC=90°,
∵AB=6,AC=8,
∴,
∵BD=CD,
∴,
∵BC∥PD,
∴∠PDC=∠BCD.
∵∠BCD=∠BAD,
∴∠BAD=∠PDC,
∵∠ABD+∠ACD=180°,∠ACD+∠PCD=180°,
∴∠ABD=∠PCD,
∴△ABD∽△DCP,
∴,即,
∴.
14.【解答】(1)证明:连接OC,
∵OC=OB,
∴∠B=∠BCO,
∴∠AOC=∠B+∠BCO=2∠B,
∵AB⊥CD,
∴∠CEO=90°,
∴∠COE+∠OCE=90°,
∵∠FCD=2∠B,
∴∠FCD=∠COE,
∴∠FCD+∠OCE=90°,
∴∠OCF=90°,
∵OC是⊙O的半径,
∴CF是⊙O的切线;
(2)解:∵AB是直径,CD是弦,且AB⊥CD,
∴CECD=6,
∵AB=20,
∴OC=10,
∴OE8,
∵∠OCF=∠OEC=90°,∠COE=∠FOC,
∴△OCE∽△OFC,
∴,
∴,
∴OF,
∴EF=OF﹣OE8.
15.【解答】解:(1)证明:连接OC
∵OB=OC
∴∠OBC=∠OCB,
∵∠DCA=∠OBC,
∴∠DCA=∠OCB,
而AB是⊙O的直径,
∴∠ACB=90°,
∴∠DCA+∠OCA=∠OCA+∠OCB=90°,
∴∠OCD=90°,
∴DC是⊙O的切线,
(2)设OC=OA=r,
∵,
∴,
∴r=8,
∴OC=OA=8,
在 Rt△OCD 中,,
∵∠DCA+∠ECF=∠BFG+∠CBA=90°,
∴∠ECF=∠BFG,
又∵∠BFG=∠EFC,
∴∠ECF=∠EFC,
∴EC=EF,设EC=EF=x,
∵∠D=∠D,∠DCO=∠DGE,
∴△DOC∽△DEG,
∴,则 ,
解得:x=14,
经检验x=14是所列方程的解,
∴CE=14.
16.【解答】(1)证明:连接OD,
在△OBD和△OBC中,
,
∴△OBD≌△OBC(SSS),
∴∠ODB=∠OCD=90°,
∴OD⊥AB,
∵OD是⊙O的半径,
∴AB是⊙O的切线;
(2)解:设⊙O的半径为R,
在Rt△OAD中,AD,AE=1,AO=AE+OE=1+R,OD=R,AD2+OD2=AO2,
∴()2+R2=(1+R)2,
解得R=1,
∴OD=1,
∴tan∠AOD,
∴∠AOD=60°,
∴∠COD=120°,
由(1)知△OBD≌△OBC,
∴∠BOD=∠BOC∠COD=60°,
∴的长.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺训练高频考点突破圆的切线的证明
1.如图,在Rt△ABC中,E为斜边AB上的一点,经过点E的⊙O与AC交于点D,连接DO,DE.若ED∥BC,∠CDO=∠B.
(1)求证:AB为⊙O的切线;
(2)若OD=BE=5,DE=6,求AC的长.
2.如图,BE是⊙O的直径,A,D是⊙O上的两点,延长BE至点C,连接AC,∠EAC=∠ABC.
(1)求证:CA是⊙O的切线;
(2),BC=10,求⊙O的半径.
3.如图,在Rt△ABC中,∠C=90°,点O在AC边上,以OA为半径的半圆O交AB于点D,交AC于点E,在BC边上取一点F,连接FD,使得DF=BF.
(1)求证:DF为半圆O的切线;
(2)若AC=6,BC=4,CF=1,求半圆O的半径长.
4.如图,AB为⊙O的直径,AD与⊙O相交于点E,∠DAB的平分线交⊙O于点C,∠ADC=90°,连DO、AC相交于点F.
(1)求证:CD是⊙O的切线;
(2)若,求cos∠DAB的值.
5.△ABC中,AB=BC,点D为AC中点,过点D作DE⊥BC于点E,点O在ED的延长线上,以O为圆心,OD为半径的圆经过点A.
(1)求证:AB是⊙O的切线;
(2)若sin∠BAC=0.6,DE=1,求BC的长.
6.如图,PA切⊙O于点A,AB是⊙O的直径,C是⊙O上一点,PA=PC=AB,连接PO交AC于点D.
(1)求证:PC是⊙O的切线;
(2)若BC=2,求AB的长.
7.如图,AB为⊙O的直径,过圆上一点D作⊙O的切线CD交BA的延长线于点C,过点O作OE∥AD交CD于点E,连接BE.
(1)求证:直线BE是⊙O的切线;
(2)若CA=2,CD=4,求DE的长.
8.如图,AB为⊙O的直径,点C在⊙O上,∠ACB的平分线CD交⊙O于点D,过点D作DE∥AB,交CB的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AC=8,BC=6,求AD及BE的长.
9.如图,△ABC中,以AB为直径的⊙O交BC于点E,AE平分∠BAC,过点E作ED⊥AC于点D,延长DE交AB的延长线于点P.
(1)求证:PE是⊙O的切线;
(2)若,BP=4,求CD的长.
10.如图,AB为⊙O的直径,C、F为⊙O上两点,且点C为弧BF的中点,过点C作AF的垂线,交AF的延长线于点E,交AB的延长线于点D.
(1)求证:DE是⊙O的切线;
(2)若AE=3,DE=4,求⊙O的半径的长.
11.如图,AB是⊙O的直径,PB⊥AB,过点B作BC⊥OP交⊙O于点C,垂足为D,连接PC并延长与BA的延长线交于点M.
(1)求证:PM是⊙O的切线;
(2)若OD=2,OP=18,求的值.
12.如图,AB是⊙O的直径,点D是⊙O上一点,过点A的切线与弦BD的延长线交于点C,过点D的直线交线段AC于点E,且DE=CE.
(1)求证:直线DE与⊙O相切;
(2)已知⊙O的半径是4,∠B=30°,求阴影部分的面积.
13.如图⊙O是△ABC的外接圆,点O在BC上,∠BAC的角平分线交⊙O于点D,连接BD,CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)若AB=6,AC=8,求DC与PC的值.
14.如图,在⊙O中,AB是直径,CD是弦,且AB⊥CD,垂足为E,AB=20,CD=12,在BA的延长线上取一点F,连接CF,使∠FCD=2∠B.
(1)求证:CF是⊙O的切线;
(2)求EF的长.
15.如图,点C在以AB为直径的⊙O上,点D在BA的延长线上,∠DCA=∠CBA.
(1)求证:DC是⊙O的切线;
(2)点G是半径OB上的点,过点G作OB的垂线与BC交于点F,与DC的延长线交于点E,若sinD,DA=FG=2,求CE的长.
16.如图,在Rt△ABC中,∠ACB=90°,点E在AC上,以CE为直径的⊙O经过AB上的点D,与OB交于点F,且BD=BC.
(1)求证:AB是⊙O的切线;
(2)若AD,AE=1,求的长.
参考答案
1.【解答】(1)证明:∵ED∥BC,∠C=90°,
∴∠AED=∠B,∠CDE=90°,
又∵∠CDO=∠B,
∴∠AED=∠CDO,
∵OD=OE,
∴∠OED=∠ODE,
∴∠AED+∠OED=∠CDO+∠ODE=90°,即∠AEO=90°,
又∵OE是半径;
∴AB为⊙O的切线;
(2)解:由(1)知∠GDE=90°,OD=BE=5,DE=6,如图,延长DC交⊙O于点G,连接OG,
∴EG是直径,即O、E、G三点共线,
∴EG=2OD=2×5=10,
在直角三角形DEG中,DE=6,
由勾股定理得:8,
∴,
又∵∠AEG=90°,
∴,
∴,
∵OD=OG,
∴∠G=∠CDO,
又∵∠CDO=∠B,
∴∠G=∠B,
∴,
在Rt△ABC中,.
2.【解答】(1)证明:连接OA,
∵OA=OB,
∴∠1=∠2,
∵∠1=∠3,
∴∠2=∠3,
∵BE是⊙O的直径,
∴∠BAE=∠2+∠OAE=90°,
∴∠3+∠OAE=90°,
∴∠OAC=90°,即OA⊥AC,
∵OA是半径,
∴CA是⊙O的切线;
(2)解:如图:
由题意可得:∠1=∠D,
∵∠BAE=90°,
∴,
∵∠1=∠3,∠C=∠C,
∴△CAE∽△CBA,
∴,
∴,
∴AC=6,,
∴,
∴.
3.【解答】(1)证明:连接OD,则OD=OA,
∴∠ODA=∠A,
∵DF=BF,
∴∠FDB=∠B,
∵∠C=90°,
∴∠ODA+∠FDB=∠A+∠B=90°,
∴∠ODF=180°﹣(∠ODA+∠FDB)=90°,
∵OD是⊙O的半径,且DF⊥OD,
∴DF是半圆O的切线.
(2)解:连接OF,设半圆O的半径长为r,
∵AC=6,BC=4,CF=1,
∴DF=BF=BC﹣CF=4﹣1=3,OC=AC﹣OA=6﹣r,
∵∠ODF=∠C=90°,
∴OD2+DF2=OC2+CF2=OF2,
∴r2+32=(6﹣r)2+12,解得r,
∴半圆O的半径长是.
4.【解答】(1)证明:∵AC平分∠DAB,
∴∠DAC=∠OAC,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠DAC=∠OCA,
∴OC∥AD,
∴∠ADC+∠OCD=180°,
∵∠ADC=90°,
∴∠OCD=90°,
∴半径OC⊥CD,
∴CD是⊙O的切线;
(2)过O作OH⊥AD于H,
由(1)知:OC∥AD,
∴△OCF∽△DAF,
∴OC:AD=CF:AF=3:4,
∴令OC=3x,AD=4x,
∴OA=OC=3x,
∵∠ADC=∠OCD=∠OHD=90°,
∴四边形DCOH是矩形,
∴DH=OC=3x,
∴AH=AD﹣DH=x,
∴cos∠DAB.
5.【解答】(1)证明:连接OA,如图,
∵AB=BC,
∴∠BAC=∠C,
∵DE⊥BC,
∴∠C+∠CDE=90°,
∵OA=OD,
∴∠OAD=∠ODA,
∵∠ODA=∠CDE,
∴∠OAD+∠BAC=∠C+∠CDE=90°,
∴AB是⊙O的切线;
(2)解:连接BD,如图,
∵AB=BC,点D为AC中点,
∴BD⊥AC,
∴∠CDE+∠BDE=∠CDE+∠C=90°,
∴∠BDE=∠C=∠BAC,
∵sin∠BAC=0.6,
∴sin∠BDE,
∴BE=0.6BD,
∵BD2﹣BE2=DE2,DE=1,
∴BD2﹣(0.6BD)2=1,
∴BD,
∴BC.
6.【解答】(1)证明:如图,连接OC,
∵PA是⊙O的切线,
∴PA⊥OA.
∴∠PAO=90°.
∵OC=OA,PC=PA,OP=OP.
∴△POC≌△POA(SSS).
∴∠PCO=∠PAO=90°.
∴PC⊥OC.
∴PC是⊙O的切线;
(2)∵∠PDA=∠ACB=90°,∠APD=∠BAC.
又∵PA=AB,
∴△PAD≌△ABC(AAS).
∴AD=BC=2,AC=2AD=4.
∴.
7.【解答】(1)证明:∵CD与⊙O相切于点D,
∴CD⊥OD,
∵OD=OA,
∴∠OAD=∠ODA,
∵OE∥AD交CD于点E,
∴∠BOE=∠OAD,∠DOE=∠ODA,
∴∠BOE=∠DOE,
∵OB=OD,OE=OE,
∴△BOE≌△DOE(SAS),
∴∠OBE=∠ODE=90°,
∵OB是⊙O的半径,且BE⊥OB,
∴直线BE是⊙O的切线.
(2)解:∵∠ODC=90°,
∴CD2+OD2=OC2,
∵CA=2,CD=4,OD=OA,
∴42+OA2=(2+OA)2,
∴OB=OD=OA=3,
∴BC=CA+OA+OB=2+3+3=8,
∵DE与⊙O相切于点D,BE与⊙O相切于点B,
∴DE=BE,
∵∠B=90°,
∴BC2+BE2=CE2,
∴82+DE2=(4+DE)2,
解得DE=6,
∴DE的长是6.
8.【解答】(1)证明:连接OD,
由角平分线定义可知∠ACD=∠BCD,
∴∠AOD=∠BOD,
∵AB为⊙O的直径,
∴,
∴OD⊥AB,
∵DE∥AB,
∴OD⊥DE,
∵OD为⊙O的半径,
∴直线DE是⊙O的切线;
(2)解:在Rt△ABC中,由勾股定理得,
由条件可知∠ACD=∠BCD,
∴,
∴,
∵DE∥AB,
∴∠BDE=∠ABD=∠ACD,
又四边形ACBD内接于⊙O,
∴∠CAD=∠DBE,
∴△BDE∽△ACD,
∴,
∴,
∴,
∴,.
9.【解答】(1)证明:如图,连接OE,
∵AE平分∠BAC,
∴∠OAE=∠DAE,
∵OE=OA,
∴∠OEA=∠OAE,
∴∠DAE=∠OEA,
∴OE∥AD,
∵ED⊥AC,
∴OE⊥PD,
∵OE是⊙O的半径,
∴PE是⊙O的切线;
(2)解:∵,BP=4,OB=OE,
∴,
∴OE=2,
∴AB=2OE=4,
∴AP=AB+BP=8,
在Rt△APD中,sin∠P,
∴ADAP,
∵AB为⊙O的直径,
∴∠AEB=90°=∠AEC,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵AE=AE,
∴△AEB≌△AEC(ASA),
∴AB=AC=4,
∴CD=AC﹣AD=4,
∴CD的长为.
10.【解答】(1)证明:连接OC,
∵点C为弧BF的中点,
∴弧BC=弧CF.
∴∠BAC=∠FAC,
∵OA=OC,
∴∠OCA=∠OAC.
∴∠OCA=∠FAC,
∴OC∥AE,
∵AE⊥DE,
∴OC⊥DE.
∴DE是⊙O的切线.
(2)解:由勾股定理得AD5,
∵∠OCD=∠AEC=90°,
∠D=∠D,
∴△OCD∽△AED,
∴,
即,
解得r,
∴⊙O的半径长为.
11.【解答】(1)证明:连接OC,
∵OC=OB,BC⊥OP,
∴∠COP=∠BOP,
∵OP=OP,
∴△PBO≌△PCO(SAS),
∴∠OCP=∠OBP,
∵PB⊥AB,
∴∠ABP=90°,
∴∠OCP=90°,
∴PM是⊙O的切线;
(2)解:连接AC,
∵∠OCP=∠CDO=90°,
∴∠OCD=∠CPO,
∴△OCD∽△OPC,
∴,
∴OC2=OD OP,
∵OD=2,OP=18,
∴OC=6,PD=OP﹣OD=16,
∴,
∴,
∴4,
∵∠ACM+∠ACO=∠OCD+∠ACO=90°,
∴∠ACM=∠OCD,
∴∠ACM=∠CPO,
∴AC∥OP,
∴△ACM∽△OPM,
∴,
∴.
12.【解答】(1)证明:连接OD、AD,则OD=OA,
∵AB是⊙O的直径,AC与⊙O相切于点A,
∴∠ADB=90°,AC⊥AB,
∴∠ADC=∠BAC=90°,
∴∠EDA=∠EDC=90°,∠EAD+∠C=90°,
∵DE=CE,
∴∠EDC=∠C,
∴∠EDA=∠EAD,
∵∠ODA=∠OAD,
∴∠ODE=∠ODA+∠EDA=∠OAD+∠EAD=∠BAC=90°,
∵OD是⊙O的半径,且DE⊥OD,
∴直线DE与⊙O相切.
(2)解:∵∠EDC=∠C,∠EDA=∠EAD,
∴CE=AE=DEAC,
∵⊙O的半径是4,∠B=30°,
∴OD=OA=OBAB=4,AB=8,∠AOD=2∠B=60°,
∴△AOD是等边三角形,
∴AD=OD=4,∠BAD=60°,
∴BD4,∠CAD=∠BAC﹣∠BAD=30°,
∴AC=2CD,
∵ADCD=4,
∴CD,
∵S△ABD4×48,S△ACD4,
∴S△AODS△ABD=4,S△AEDS△ACD,
∵S扇形AOD,
∴S阴影=S△AOD+S△AED﹣S扇形AOD=4,
∴阴影部分的面积为.
13.【解答】(1)证明:如图1,连接OD,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴,
∴∠BOD=∠COD=90°,
∵BC∥PD,
∴∠ODP=∠BOD=90°,
∴OD⊥PD,
∵OD是半径,
∴PD是⊙O的切线;
(2)解:∵BC是⊙O的直径,
∴∠BAC=∠BDC=90°,
∵AB=6,AC=8,
∴,
∵BD=CD,
∴,
∵BC∥PD,
∴∠PDC=∠BCD.
∵∠BCD=∠BAD,
∴∠BAD=∠PDC,
∵∠ABD+∠ACD=180°,∠ACD+∠PCD=180°,
∴∠ABD=∠PCD,
∴△ABD∽△DCP,
∴,即,
∴.
14.【解答】(1)证明:连接OC,
∵OC=OB,
∴∠B=∠BCO,
∴∠AOC=∠B+∠BCO=2∠B,
∵AB⊥CD,
∴∠CEO=90°,
∴∠COE+∠OCE=90°,
∵∠FCD=2∠B,
∴∠FCD=∠COE,
∴∠FCD+∠OCE=90°,
∴∠OCF=90°,
∵OC是⊙O的半径,
∴CF是⊙O的切线;
(2)解:∵AB是直径,CD是弦,且AB⊥CD,
∴CECD=6,
∵AB=20,
∴OC=10,
∴OE8,
∵∠OCF=∠OEC=90°,∠COE=∠FOC,
∴△OCE∽△OFC,
∴,
∴,
∴OF,
∴EF=OF﹣OE8.
15.【解答】解:(1)证明:连接OC
∵OB=OC
∴∠OBC=∠OCB,
∵∠DCA=∠OBC,
∴∠DCA=∠OCB,
而AB是⊙O的直径,
∴∠ACB=90°,
∴∠DCA+∠OCA=∠OCA+∠OCB=90°,
∴∠OCD=90°,
∴DC是⊙O的切线,
(2)设OC=OA=r,
∵,
∴,
∴r=8,
∴OC=OA=8,
在 Rt△OCD 中,,
∵∠DCA+∠ECF=∠BFG+∠CBA=90°,
∴∠ECF=∠BFG,
又∵∠BFG=∠EFC,
∴∠ECF=∠EFC,
∴EC=EF,设EC=EF=x,
∵∠D=∠D,∠DCO=∠DGE,
∴△DOC∽△DEG,
∴,则 ,
解得:x=14,
经检验x=14是所列方程的解,
∴CE=14.
16.【解答】(1)证明:连接OD,
在△OBD和△OBC中,
,
∴△OBD≌△OBC(SSS),
∴∠ODB=∠OCD=90°,
∴OD⊥AB,
∵OD是⊙O的半径,
∴AB是⊙O的切线;
(2)解:设⊙O的半径为R,
在Rt△OAD中,AD,AE=1,AO=AE+OE=1+R,OD=R,AD2+OD2=AO2,
∴()2+R2=(1+R)2,
解得R=1,
∴OD=1,
∴tan∠AOD,
∴∠AOD=60°,
∴∠COD=120°,
由(1)知△OBD≌△OBC,
∴∠BOD=∠BOC∠COD=60°,
∴的长.
21世纪教育网(www.21cnjy.com)
同课章节目录
