人教版2024—2025学年八年级下册数学期中考试模拟试卷(含解析)
文档属性
| 名称 | 人教版2024—2025学年八年级下册数学期中考试模拟试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 576.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-04 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版2024—2025学年八年级下册数学期中考试模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下面各组数是三角形三边长,其中为直角三角形的是( )
A.8,12,15 B.5,6,8 C.8,15,17 D.10,15,20
2.下列二次根式中的最简二次根式是( )
A. B. C. D.
3.下列命题是假命题的是( )
A.两组边相等的四边形是平行四边形
B.对角线互相垂直且平分的四边形是菱形
C.有三个角是直角的四边形是矩形
D.有一组邻边相等的矩形是正方形
4.如图,在Rt△ABC中,∠B=90°,BC=12,AB=5,则斜边上的中线BO长是( )
A.2.5 B.4 C.6 D.6.5
5.如图,在平行四边形ABCD中,AB=4,BC=7,∠ABC的平分线交AD于点E,则ED是( )
A.2 B.3 C.4 D.5
6.正方形具有而菱形不具有的性质是( )
A.对角线平分一组对角 B.对角线相等
C.对角线互相垂直平分 D.四条边相等
7.如图,则化简的结果为( )
A.﹣1 B.1 C.2a﹣1 D.1﹣2a
8.数学课上,老师要同学们判断一个四边形门框是否为矩形.下面是某合作小组的4位同学拟定的方案,其中正确的是( )
A.测量对角线是否互相平分 B.测量两组对边是否分别相等
C.测量一组对角是否都为直角 D.测量三个角是否为直角
9.如图,在菱形ABCD中,AC、BD交于O点,AC=8,BD=6,点P为线段AC上的一个动点,过点P分别作PM⊥AD于点M,作PN⊥DC于点N,则PM+PN的值为( )
A. B. C. D.
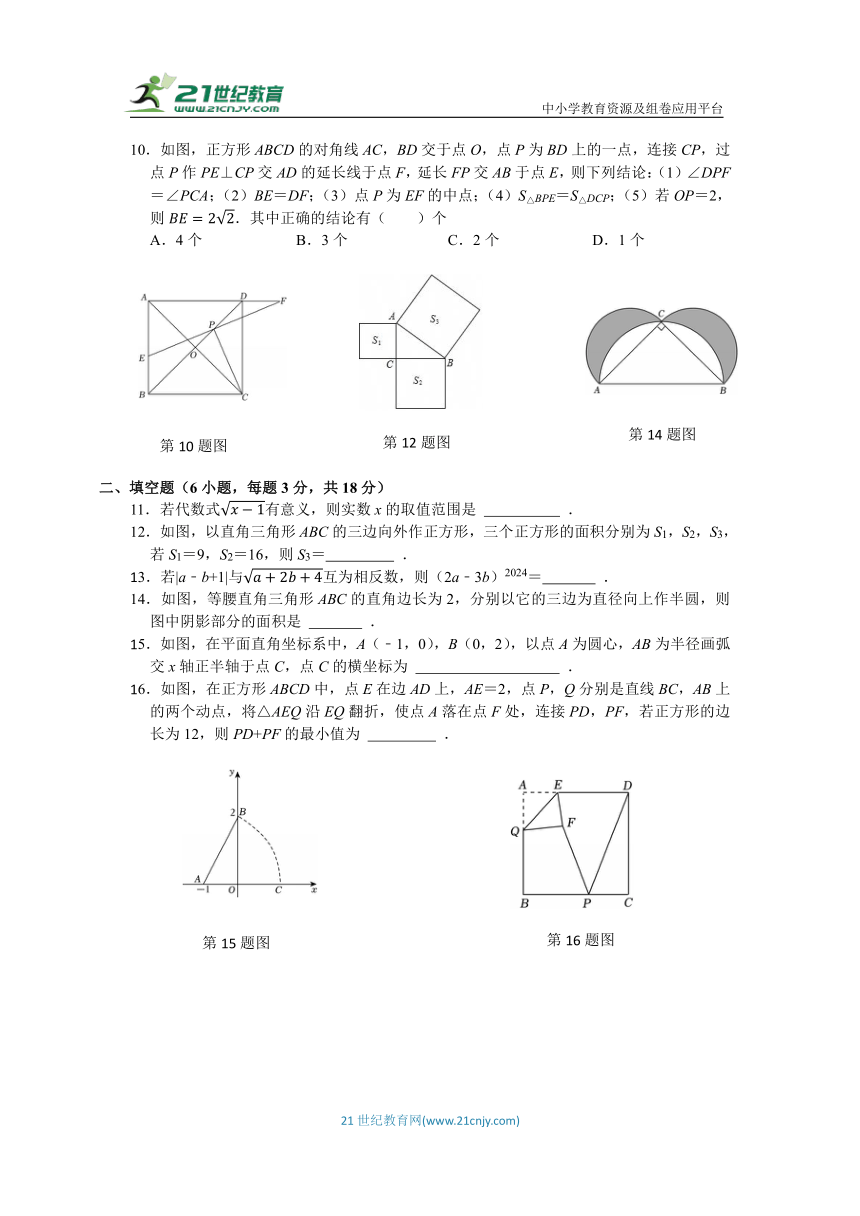
10.如图,正方形ABCD的对角线AC,BD交于点O,点P为BD上的一点,连接CP,过点P作PE⊥CP交AD的延长线于点F,延长FP交AB于点E,则下列结论:(1)∠DPF=∠PCA;(2)BE=DF;(3)点P为EF的中点;(4)S△BPE=S△DCP;(5)若OP=2,则.其中正确的结论有( )个
A.4个 B.3个 C.2个 D.1个
二、填空题(6小题,每题3分,共18分)
11.若代数式有意义,则实数x的取值范围是 .
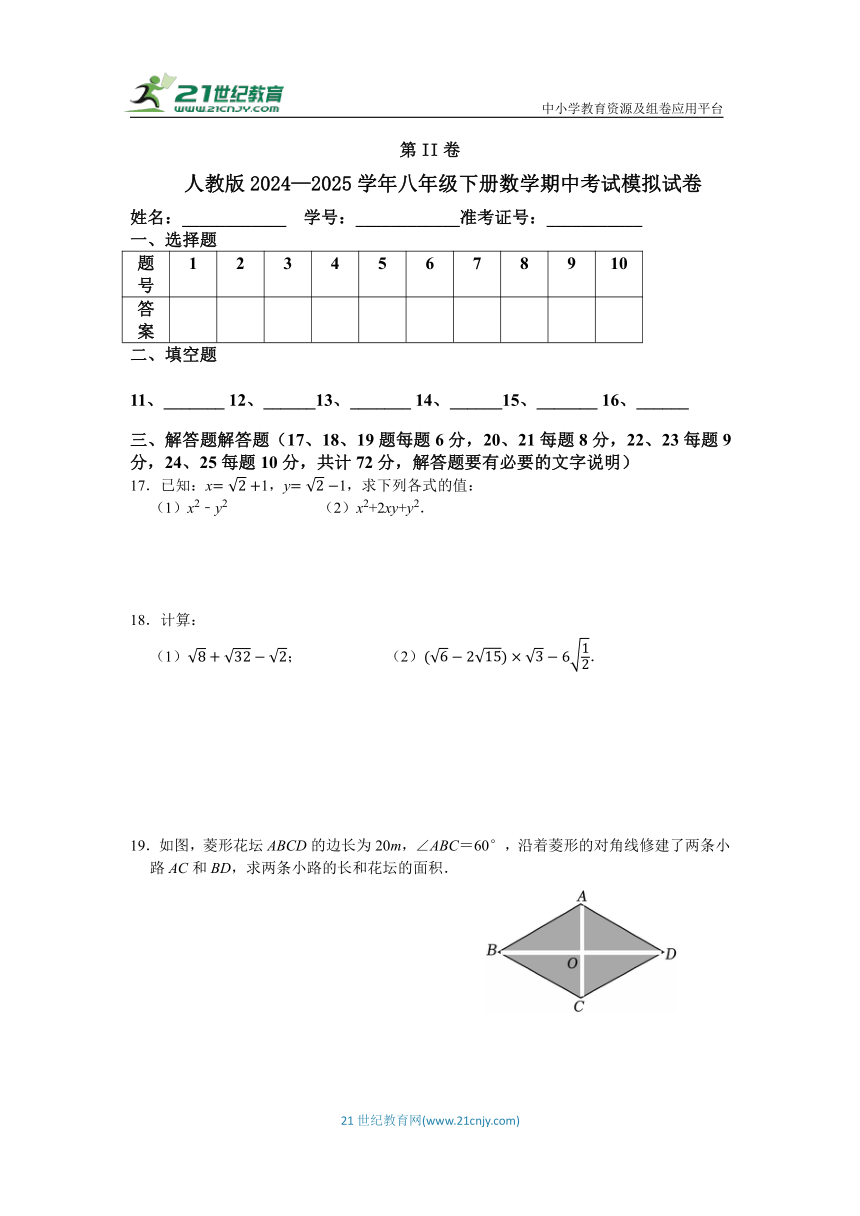
12.如图,以直角三角形ABC的三边向外作正方形,三个正方形的面积分别为S1,S2,S3,若S1=9,S2=16,则S3= .
13.若|a﹣b+1|与互为相反数,则(2a﹣3b)2024= .
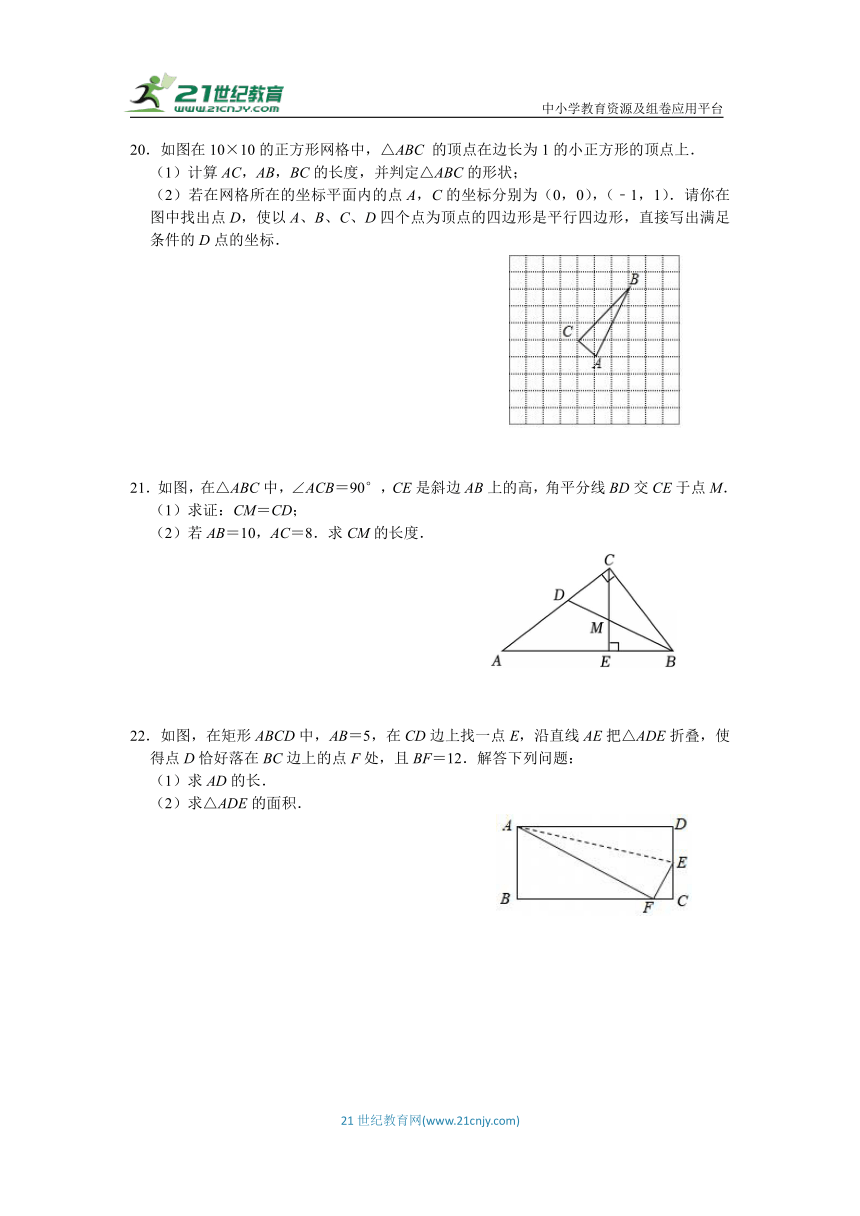
14.如图,等腰直角三角形ABC的直角边长为2,分别以它的三边为直径向上作半圆,则图中阴影部分的面积是 .
15.如图,在平面直角坐标系中,A(﹣1,0),B(0,2),以点A为圆心,AB为半径画弧交x轴正半轴于点C,点C的横坐标为 .
16.如图,在正方形ABCD中,点E在边AD上,AE=2,点P,Q分别是直线BC,AB上的两个动点,将△AEQ沿EQ翻折,使点A落在点F处,连接PD,PF,若正方形的边长为12,则PD+PF的最小值为 .
第II卷
人教版2024—2025学年八年级下册数学期中考试模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.已知:x1,y1,求下列各式的值:
(1)x2﹣y2 (2)x2+2xy+y2.
18.计算:
(1); (2).
19.如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积.
20.如图在10×10的正方形网格中,△ABC 的顶点在边长为1的小正方形的顶点上.
(1)计算AC,AB,BC的长度,并判定△ABC的形状;
(2)若在网格所在的坐标平面内的点A,C的坐标分别为(0,0),(﹣1,1).请你在图中找出点D,使以A、B、C、D四个点为顶点的四边形是平行四边形,直接写出满足条件的D点的坐标.
21.如图,在△ABC中,∠ACB=90°,CE是斜边AB上的高,角平分线BD交CE于点M.
(1)求证:CM=CD;
(2)若AB=10,AC=8.求CM的长度.
22.如图,在矩形ABCD中,AB=5,在CD边上找一点E,沿直线AE把△ADE折叠,使得点D恰好落在BC边上的点F处,且BF=12.解答下列问题:
(1)求AD的长.
(2)求△ADE的面积.
23.观察下列各式及其变形过程:
;
;
;
…
(1)按照此规律写出第五个等式a5= .
(2)按照此规律,若sn=a1+a2+a3+…+an,当n=4时,s4= .
(3)在(2)的条件下,若,试求x的值.
24.已知:如图,在正方形ABCD中,E,F分别是BC,CD上的点,AE、BF相交于点P,并且AE=BF.
(1)如图1,判断AE和BF的位置关系?并说明理由;
(2)若AB=8,BE=6,求BP的长度;
(3)如图2,FM⊥DN,DN⊥AE,点F在线段CD上运动时(点F不与C、D重合),四边形FMNP是否能否成为正方形?请说明理由.
25.在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,A,C两点坐标分别为A(0,a),C(c,0).
(1)若,直接写出A,C两点坐标;
(2)在(1)的条件下,如图1,F为AB延长线上一点,∠OCF的平分线交y轴于点E,若,求CF的长.
(3)如图2,M、N分别为AB、AO上的点,若∠AMN=∠MCN=45°,试探究ON2、BM2、MN2之间的数量关系并证明.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A D B B D D C A
1.【解答】解:∵82+122=64+144=208≠225=152,故选项A不符合题意;
∵52+62=25+36=61≠64=82,故选项B不符合题意;
∵82+152=64+225=289=172,故选项C符合题意;
∵102+152=100+225=325≠400=202,故选项D不符合题意;
故选:C.
2.【解答】解:A、2,故不是最简二次根式,本选项错误;
B、2,故不是最简二次根式,本选项错误;
C、,故不是最简二次根式,本选项错误;
D、是最简二次根式,本选项正确.
故选:D.
3.【解答】解:两组对边分别相等的四边形是平行四边形,原说法是假命题,不符合题意;
对角线互相垂直且平分的四边形是菱形,是真命题,符合题意;
有三个角是直角的四边形是矩形,是真命题,不符合题意;
有一组邻边相等的矩形是正方形,是真命题,不符合题意,
故选:A.
4.【解答】解:∵在Rt△ABC中,∠B=90°,BC=12,AB=5,
∴AC13,
∴斜边上的中线BOAC=6.5.
故选:D.
5.【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=7,
∴∠AEB=∠CBE,
又∵BE平分∠ABC,
∴∠ABE=∠CBE=∠AEB,
∴AE=AB=4,
∴DE=AD﹣AE=7﹣4=3,
故选:B.
6.【解答】解:正方形的边:四边都相等,菱形的边四边都相等;
正方形的角:四角都相等,都是直角,菱形的角:对角相等;
正方形的对角线:相等,互相平分,且互相垂直,菱形的对角线:互相平分,互相垂直.
则:正方形具有而菱形不具有的性质是:对角线相等.
故选:B.
7.【解答】解:由题意得0<a<1,
∴a﹣1<0,
∴.
故选:D.
8.【解答】解:A、对角线是否相互平分,只能判定平行四边形;
B、两组对边是否分别相等,只能判定平行四边形;
C、一组对角是否都为直角,不能判定形状;
D、其中四边形中三个角都为直角,能判定矩形.
故选:D.
9.【解答】解:如图,连接PD,
∵四边形ABCD是菱形,
∴AC与BD互相垂直平分,
∴AO=OC=4,BO=DO=3,
∴,
∵S△ACD=S△APD+S△CPD,PM⊥AD,PN⊥CD,
∴,
∴8×3=5(PM+PN),
∴PM+PN,
故选:C.
10.【解答】解:∵四边形ABCD是正方形,
∴AC⊥BD,
∴∠BAD=∠ADC=∠ABC=∠BCD=90°,
∵PF⊥CP,
∴∠COD=∠CPE=90°,
∴∠BPE=∠PCA=90°﹣∠BPC,
∵∠DPF=∠BPF,
∴∠DPF=∠PCA,
故(1)正确;
连接PA,CE,CF,设EF交CD于H,
则∠DHF=∠PHC,
∵AD=CD,BD⊥AC,
∴∠ADB=∠CDB=45°,
在△ADP和△CDP中,
,
∴△ADP≌△CDP(SAS),
∴PA=PC,∠PAD=∠PCD,
∵∠CDF=∠CPF=90°,
∴∠PFD=90°﹣∠DHF=90°﹣∠PHC=∠PCD,
∴∠PFD=∠PAD,
∴PF=PA=PC,
∵∠PEA+∠PFD=90°,∠PAE+∠PAD=90°,
∴∠PEA=∠PAE,
∴PE=PF=PA=PC,
∴P为EF中点,
故(3)正确;
∵∠PCE=∠PEC=45°,∠PCF=∠PFC=45°,PC垂直平分EF,
∴∠ECF=90°,CE=CF,
∴∠BCE=∠DCF=90°﹣∠DCE,
在△BCE和△DCF中,
,
∴△BCE≌△DCF(ASA),
∴BE=DF,
故(2)正确;
∵当OP逐渐变小时,则S△BPE的值逐渐变小,而S△DCP逐渐变大,
∴S△BPE与S△DCP不一定相等,
故(4)错误;
作EG⊥BD于点G,
∴∠BGE=∠PGE=90°,
∴∠PGE=∠COP=90°,
∴∠GPE=∠OCP=90°﹣∠OPC,
在△GPE和△OCP中,
,
∴△GPE≌△OCP(AAS),
∴GE=OP=2,
∵AB=CB,BD⊥AC,
∴,
∴∠GEB=∠GBE=45°,
∴GE=GB=2,
∴,
故(5)正确;
综上所述:(1)(2)(3)(5)这4个正确;
故选:A.
二、填空题
11.【解答】解:要使代数式有意义,必须x﹣1≥0,
解得:x≥1.
故答案为:x≥1.
12.【解答】解:由勾股定理得,AB2=AC2+BC2,
∴S3=S1+S2=9+16=25,
故答案为:25.
13.【解答】解:∵|a﹣b+1|和互为相反数,
∴|a﹣b+1|0,
∴,
∴a=﹣2,b=﹣1,
∴(2a﹣3b)2024=[2×(﹣2)﹣3×(﹣1)]2024=1.
故答案为:1.
14.【解答】解:S半圆ACS半圆BC,
,
S半圆AB,
∴图中阴影部分的面积=S半圆AC+S半圆BC+S△ABC﹣S半圆AB
=2,
故答案为:2.
15.【解答】解:∵A(﹣1,0),B(0,2),
∴OA=1,OB=2,
在Rt△AOB中,由勾股定理得:AB,
∴AC=AB,
∴OC1,
∴点C的横坐标为1.
故答案为:1.
16.【解答】解:由题意知,DE=AD﹣AE=10,
由翻折的性质可知,EF=AE=2,
如图,作D关于BC的对称点D′,连接PD′,则PD′=PD,
∴DD′=2CD=24,PD+PF=PD′+PF,
∴EF+PD+PF=PD′+PF+EF,
∴当E、F、P、D′四点共线时,PD+PF的值最小,
如图,连接ED′,则PD+PF的最小值为ED′﹣EF,
在直角三角形DD′E中,由勾股定理得,
∴ED′﹣EF=24,
故答案为:24.
三、解答题
17.【解答】解:(1)∵x1,y1,
∴x2﹣y2
=(x+y)(x﹣y)
=()()
2
=4;
(2)x2+2xy+y2
=(x+y)2
=()2
=(2)2
=8.
18.【解答】解:(1)
=5;
(2)
=3
.
19.【解答】解:∵花坛ABCD是菱形,
∴AC⊥BD,AC=2AO,BD=2BO,,
∴Rt△ABO中,,
∴,
∴AC=2AO=20m,,
∵,
∴菱形花坛的面积是.
20.【解答】解:
(1)∵小正方形的边长为1,
∴AC,BC3,AB2,
∴AC2+BC2=AB2,
∴△ABC为直角三角形;
(2)∵A,C的坐标分别为(0,0),(﹣1,1),
∴点C为坐标原点,
如图,分别过A作BC的平行线,过B作AC的平行线,过C作AB的平行线,
∴满足条件的点D的坐标为(3,3)或(1,5)或(﹣3,﹣3).
21.【解答】(1)证明:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵∠ACB=90°,CE是斜边AB上的高,
∴∠CEB=∠ACB=90°,
∴∠ABD+∠BME=∠CBD+∠CDM=90°,
∴∠BME=∠CDM,
∵∠BME=∠CMD,
∴∠CDM=∠CMD,
∴CD=CM;
(2)解:在Rt△ABC中,AB=10,AC=8.
∴,
如图,过点D作DF⊥AB于点F,
∵BD平分∠ABC,∠ACB=90°,
∴CD=FD,
在Rt△BCD和Rt△BFD中,
∵BD=BD,CD=FD,
∴Rt△BCD≌Rt△BFD(HL),
∴BF=BC=6,
∴AF=4,
在Rt△ADF中,AD2=DF2+AF2,
∴(8﹣CD)2=CD2+42,
解得:CD=3,
∵CD=CM,
∴CM=3.
22.【解答】解:(1)在Rt△ABF中,AB=5,BF=12,由勾股定理得,
AF13,
由翻折变换可得,
AD=AF=13;
(2)由翻折变换得,ED=EF,
设ED=x,则EC=5﹣x,FC=BC﹣BG=13﹣12=1,
在Rt△EFC中,由勾股定理得,
EC2+FC2=EF2,
即(5﹣x)2+12=x2,
解得x,
即DE,
∴S△ADEAD DE
13
,
答:△ADE的面积为.
23.【解答】解:(1)由式子的变化规律得:,
故答案是:;
(2)sn=a1+a2+a3+ +an
,
当n=4时,;
(3)∵
.
24.【解答】解:(1)AE⊥BF,理由如下:
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°,
在Rt△ABE和Rt△BCF中,
,
∴Rt△ABE≌Rt△BCF(HL),
∴∠BAE=∠CBF,
∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴AE⊥BF;
(2)在Rt△ABE中,AB=8,BE=6,
根据勾股定理得:AE10,
∵S△ABEAB BEAE BP,
∴8×6=10BP,
∴BP=4.8,
∴BP的长度为4.8;
(3)四边形FMNP不能成为正方形,理由如下:
由(1)知:AE⊥BF,
∴∠APF=90°,
∵FM⊥DN,DN⊥AE,
∴∠FMN=∠MNP=90°,
∴四边形FMNP是矩形,
∵∠BAP+∠NAD=∠NAD+∠ADN=90°,
∴∠BAP=∠ADN,
在△BAP和△ADN中,
,
∴△BAP≌△ADN(ASA),
∴AN=BP,AP=DN,
∵AE=BF,
∴AE﹣AN=BF﹣BP,
∴EN=PF,
∵点F在线段CD上运动时(点F不与C、D重合),
∴P、E不重合,
∴PN≠PF,
∴四边形FMNP不能成为正方形.
25.【解答】解:(1)∵,
∴24﹣2c≥0,c﹣12≥0,
∴c=12,
∴a=c=12,
∴A(0,12),C(12,0);
(2)∵四边形OABC是矩形,A(0,12),C(12,0),
∴OC=OA=AB=BC=12,AB∥OC,
∵,
∴OE18,
∴AE=6,
如图,若AB与CE交点G,取BG的中点K,CG的中点H,连接KH,则GK=KB,
∴KH是△BCG的中位线,
∴,KH∥BC,
∴KH=AE=6,∠GKH=∠GAE,∠GHK=∠GEA,
∴△AGE≌△KGH(ASA),
∴GK=AG,
∴AG=GK=KB,
∵AB=12,
∴AG=GK=KB=4,
∵∠OCF的平分线交y轴于点E,
∴∠FCG=∠OCE,
∵AB∥OC,
∴∠BGC=∠OCE,
∴∠FCG=∠OCE=∠BGC,
∴CF=FG,
∴BF=FG﹣BG=CF﹣8,
∵BF2+BC2=CF2,
∴(CF﹣8)2+122=CF2,
解得CF=13;
(3)ON2、BM2、MN2之间的数量关系为BM2+ON2MN2,
证明:∵四边形OABC是矩形,A,C两点坐标分别为A(0,a),C(c,0),
∴OA=BC=a,OC=AB=c,
设AM=x,则BM=c﹣x,
∵∠AMN=45°,
∴AM=AN=x,,
∴ON=a﹣x,
过C向下作PC⊥CM,使PC=CM,过P作PD⊥x轴于D,过N作NQ⊥PD于点Q,
∴∠PDC=∠B=∠BCO=90°,∠PCD=∠BCM=90°﹣∠DCM,
∴△PCD≌△MCB(AAS),
∴CD=CB=a,PD=BM=c﹣x,BC=CD=a,
∴OD=a﹣c,
∵∠MCN=45°,
∴∠BCM+∠DCN=∠PCD+∠DCN=45°,
∴∠MCN=∠PCN=45°,
∵PC=CM,CN=CN,
∴△CMN≌△CPN(SAS),
∴,
∵PD⊥x轴,NQ⊥PD,∠NOD=90°,
∴∠ODQ=∠Q=∠NOD=90°,
∴四边形ONQD是矩形,
∴QD=ON=a﹣x,QN=OD=a﹣c,
∴PQ=PD+QD=a﹣x+c﹣x=a+c﹣2x,
∵PQ2+QN2=PN2,
∴,
∴a2+c2﹣2ax﹣2cx=﹣x2,
∵BM=c﹣x,,ON=a﹣x,
∴BM2+ON2=(c﹣x)2+(a﹣x)2=a2+c2﹣2ax﹣2cx+2x2=﹣x2+2x2=x2,MN2=2x2,
∴BM2+ON2MN2.
21世纪教育网(www.21cnjy.com)
人教版2024—2025学年八年级下册数学期中考试模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下面各组数是三角形三边长,其中为直角三角形的是( )
A.8,12,15 B.5,6,8 C.8,15,17 D.10,15,20
2.下列二次根式中的最简二次根式是( )
A. B. C. D.
3.下列命题是假命题的是( )
A.两组边相等的四边形是平行四边形
B.对角线互相垂直且平分的四边形是菱形
C.有三个角是直角的四边形是矩形
D.有一组邻边相等的矩形是正方形
4.如图,在Rt△ABC中,∠B=90°,BC=12,AB=5,则斜边上的中线BO长是( )
A.2.5 B.4 C.6 D.6.5
5.如图,在平行四边形ABCD中,AB=4,BC=7,∠ABC的平分线交AD于点E,则ED是( )
A.2 B.3 C.4 D.5
6.正方形具有而菱形不具有的性质是( )
A.对角线平分一组对角 B.对角线相等
C.对角线互相垂直平分 D.四条边相等
7.如图,则化简的结果为( )
A.﹣1 B.1 C.2a﹣1 D.1﹣2a
8.数学课上,老师要同学们判断一个四边形门框是否为矩形.下面是某合作小组的4位同学拟定的方案,其中正确的是( )
A.测量对角线是否互相平分 B.测量两组对边是否分别相等
C.测量一组对角是否都为直角 D.测量三个角是否为直角
9.如图,在菱形ABCD中,AC、BD交于O点,AC=8,BD=6,点P为线段AC上的一个动点,过点P分别作PM⊥AD于点M,作PN⊥DC于点N,则PM+PN的值为( )
A. B. C. D.
10.如图,正方形ABCD的对角线AC,BD交于点O,点P为BD上的一点,连接CP,过点P作PE⊥CP交AD的延长线于点F,延长FP交AB于点E,则下列结论:(1)∠DPF=∠PCA;(2)BE=DF;(3)点P为EF的中点;(4)S△BPE=S△DCP;(5)若OP=2,则.其中正确的结论有( )个
A.4个 B.3个 C.2个 D.1个
二、填空题(6小题,每题3分,共18分)
11.若代数式有意义,则实数x的取值范围是 .
12.如图,以直角三角形ABC的三边向外作正方形,三个正方形的面积分别为S1,S2,S3,若S1=9,S2=16,则S3= .
13.若|a﹣b+1|与互为相反数,则(2a﹣3b)2024= .
14.如图,等腰直角三角形ABC的直角边长为2,分别以它的三边为直径向上作半圆,则图中阴影部分的面积是 .
15.如图,在平面直角坐标系中,A(﹣1,0),B(0,2),以点A为圆心,AB为半径画弧交x轴正半轴于点C,点C的横坐标为 .
16.如图,在正方形ABCD中,点E在边AD上,AE=2,点P,Q分别是直线BC,AB上的两个动点,将△AEQ沿EQ翻折,使点A落在点F处,连接PD,PF,若正方形的边长为12,则PD+PF的最小值为 .
第II卷
人教版2024—2025学年八年级下册数学期中考试模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.已知:x1,y1,求下列各式的值:
(1)x2﹣y2 (2)x2+2xy+y2.
18.计算:
(1); (2).
19.如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积.
20.如图在10×10的正方形网格中,△ABC 的顶点在边长为1的小正方形的顶点上.
(1)计算AC,AB,BC的长度,并判定△ABC的形状;
(2)若在网格所在的坐标平面内的点A,C的坐标分别为(0,0),(﹣1,1).请你在图中找出点D,使以A、B、C、D四个点为顶点的四边形是平行四边形,直接写出满足条件的D点的坐标.
21.如图,在△ABC中,∠ACB=90°,CE是斜边AB上的高,角平分线BD交CE于点M.
(1)求证:CM=CD;
(2)若AB=10,AC=8.求CM的长度.
22.如图,在矩形ABCD中,AB=5,在CD边上找一点E,沿直线AE把△ADE折叠,使得点D恰好落在BC边上的点F处,且BF=12.解答下列问题:
(1)求AD的长.
(2)求△ADE的面积.
23.观察下列各式及其变形过程:
;
;
;
…
(1)按照此规律写出第五个等式a5= .
(2)按照此规律,若sn=a1+a2+a3+…+an,当n=4时,s4= .
(3)在(2)的条件下,若,试求x的值.
24.已知:如图,在正方形ABCD中,E,F分别是BC,CD上的点,AE、BF相交于点P,并且AE=BF.
(1)如图1,判断AE和BF的位置关系?并说明理由;
(2)若AB=8,BE=6,求BP的长度;
(3)如图2,FM⊥DN,DN⊥AE,点F在线段CD上运动时(点F不与C、D重合),四边形FMNP是否能否成为正方形?请说明理由.
25.在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,A,C两点坐标分别为A(0,a),C(c,0).
(1)若,直接写出A,C两点坐标;
(2)在(1)的条件下,如图1,F为AB延长线上一点,∠OCF的平分线交y轴于点E,若,求CF的长.
(3)如图2,M、N分别为AB、AO上的点,若∠AMN=∠MCN=45°,试探究ON2、BM2、MN2之间的数量关系并证明.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A D B B D D C A
1.【解答】解:∵82+122=64+144=208≠225=152,故选项A不符合题意;
∵52+62=25+36=61≠64=82,故选项B不符合题意;
∵82+152=64+225=289=172,故选项C符合题意;
∵102+152=100+225=325≠400=202,故选项D不符合题意;
故选:C.
2.【解答】解:A、2,故不是最简二次根式,本选项错误;
B、2,故不是最简二次根式,本选项错误;
C、,故不是最简二次根式,本选项错误;
D、是最简二次根式,本选项正确.
故选:D.
3.【解答】解:两组对边分别相等的四边形是平行四边形,原说法是假命题,不符合题意;
对角线互相垂直且平分的四边形是菱形,是真命题,符合题意;
有三个角是直角的四边形是矩形,是真命题,不符合题意;
有一组邻边相等的矩形是正方形,是真命题,不符合题意,
故选:A.
4.【解答】解:∵在Rt△ABC中,∠B=90°,BC=12,AB=5,
∴AC13,
∴斜边上的中线BOAC=6.5.
故选:D.
5.【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=7,
∴∠AEB=∠CBE,
又∵BE平分∠ABC,
∴∠ABE=∠CBE=∠AEB,
∴AE=AB=4,
∴DE=AD﹣AE=7﹣4=3,
故选:B.
6.【解答】解:正方形的边:四边都相等,菱形的边四边都相等;
正方形的角:四角都相等,都是直角,菱形的角:对角相等;
正方形的对角线:相等,互相平分,且互相垂直,菱形的对角线:互相平分,互相垂直.
则:正方形具有而菱形不具有的性质是:对角线相等.
故选:B.
7.【解答】解:由题意得0<a<1,
∴a﹣1<0,
∴.
故选:D.
8.【解答】解:A、对角线是否相互平分,只能判定平行四边形;
B、两组对边是否分别相等,只能判定平行四边形;
C、一组对角是否都为直角,不能判定形状;
D、其中四边形中三个角都为直角,能判定矩形.
故选:D.
9.【解答】解:如图,连接PD,
∵四边形ABCD是菱形,
∴AC与BD互相垂直平分,
∴AO=OC=4,BO=DO=3,
∴,
∵S△ACD=S△APD+S△CPD,PM⊥AD,PN⊥CD,
∴,
∴8×3=5(PM+PN),
∴PM+PN,
故选:C.
10.【解答】解:∵四边形ABCD是正方形,
∴AC⊥BD,
∴∠BAD=∠ADC=∠ABC=∠BCD=90°,
∵PF⊥CP,
∴∠COD=∠CPE=90°,
∴∠BPE=∠PCA=90°﹣∠BPC,
∵∠DPF=∠BPF,
∴∠DPF=∠PCA,
故(1)正确;
连接PA,CE,CF,设EF交CD于H,
则∠DHF=∠PHC,
∵AD=CD,BD⊥AC,
∴∠ADB=∠CDB=45°,
在△ADP和△CDP中,
,
∴△ADP≌△CDP(SAS),
∴PA=PC,∠PAD=∠PCD,
∵∠CDF=∠CPF=90°,
∴∠PFD=90°﹣∠DHF=90°﹣∠PHC=∠PCD,
∴∠PFD=∠PAD,
∴PF=PA=PC,
∵∠PEA+∠PFD=90°,∠PAE+∠PAD=90°,
∴∠PEA=∠PAE,
∴PE=PF=PA=PC,
∴P为EF中点,
故(3)正确;
∵∠PCE=∠PEC=45°,∠PCF=∠PFC=45°,PC垂直平分EF,
∴∠ECF=90°,CE=CF,
∴∠BCE=∠DCF=90°﹣∠DCE,
在△BCE和△DCF中,
,
∴△BCE≌△DCF(ASA),
∴BE=DF,
故(2)正确;
∵当OP逐渐变小时,则S△BPE的值逐渐变小,而S△DCP逐渐变大,
∴S△BPE与S△DCP不一定相等,
故(4)错误;
作EG⊥BD于点G,
∴∠BGE=∠PGE=90°,
∴∠PGE=∠COP=90°,
∴∠GPE=∠OCP=90°﹣∠OPC,
在△GPE和△OCP中,
,
∴△GPE≌△OCP(AAS),
∴GE=OP=2,
∵AB=CB,BD⊥AC,
∴,
∴∠GEB=∠GBE=45°,
∴GE=GB=2,
∴,
故(5)正确;
综上所述:(1)(2)(3)(5)这4个正确;
故选:A.
二、填空题
11.【解答】解:要使代数式有意义,必须x﹣1≥0,
解得:x≥1.
故答案为:x≥1.
12.【解答】解:由勾股定理得,AB2=AC2+BC2,
∴S3=S1+S2=9+16=25,
故答案为:25.
13.【解答】解:∵|a﹣b+1|和互为相反数,
∴|a﹣b+1|0,
∴,
∴a=﹣2,b=﹣1,
∴(2a﹣3b)2024=[2×(﹣2)﹣3×(﹣1)]2024=1.
故答案为:1.
14.【解答】解:S半圆ACS半圆BC,
,
S半圆AB,
∴图中阴影部分的面积=S半圆AC+S半圆BC+S△ABC﹣S半圆AB
=2,
故答案为:2.
15.【解答】解:∵A(﹣1,0),B(0,2),
∴OA=1,OB=2,
在Rt△AOB中,由勾股定理得:AB,
∴AC=AB,
∴OC1,
∴点C的横坐标为1.
故答案为:1.
16.【解答】解:由题意知,DE=AD﹣AE=10,
由翻折的性质可知,EF=AE=2,
如图,作D关于BC的对称点D′,连接PD′,则PD′=PD,
∴DD′=2CD=24,PD+PF=PD′+PF,
∴EF+PD+PF=PD′+PF+EF,
∴当E、F、P、D′四点共线时,PD+PF的值最小,
如图,连接ED′,则PD+PF的最小值为ED′﹣EF,
在直角三角形DD′E中,由勾股定理得,
∴ED′﹣EF=24,
故答案为:24.
三、解答题
17.【解答】解:(1)∵x1,y1,
∴x2﹣y2
=(x+y)(x﹣y)
=()()
2
=4;
(2)x2+2xy+y2
=(x+y)2
=()2
=(2)2
=8.
18.【解答】解:(1)
=5;
(2)
=3
.
19.【解答】解:∵花坛ABCD是菱形,
∴AC⊥BD,AC=2AO,BD=2BO,,
∴Rt△ABO中,,
∴,
∴AC=2AO=20m,,
∵,
∴菱形花坛的面积是.
20.【解答】解:
(1)∵小正方形的边长为1,
∴AC,BC3,AB2,
∴AC2+BC2=AB2,
∴△ABC为直角三角形;
(2)∵A,C的坐标分别为(0,0),(﹣1,1),
∴点C为坐标原点,
如图,分别过A作BC的平行线,过B作AC的平行线,过C作AB的平行线,
∴满足条件的点D的坐标为(3,3)或(1,5)或(﹣3,﹣3).
21.【解答】(1)证明:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵∠ACB=90°,CE是斜边AB上的高,
∴∠CEB=∠ACB=90°,
∴∠ABD+∠BME=∠CBD+∠CDM=90°,
∴∠BME=∠CDM,
∵∠BME=∠CMD,
∴∠CDM=∠CMD,
∴CD=CM;
(2)解:在Rt△ABC中,AB=10,AC=8.
∴,
如图,过点D作DF⊥AB于点F,
∵BD平分∠ABC,∠ACB=90°,
∴CD=FD,
在Rt△BCD和Rt△BFD中,
∵BD=BD,CD=FD,
∴Rt△BCD≌Rt△BFD(HL),
∴BF=BC=6,
∴AF=4,
在Rt△ADF中,AD2=DF2+AF2,
∴(8﹣CD)2=CD2+42,
解得:CD=3,
∵CD=CM,
∴CM=3.
22.【解答】解:(1)在Rt△ABF中,AB=5,BF=12,由勾股定理得,
AF13,
由翻折变换可得,
AD=AF=13;
(2)由翻折变换得,ED=EF,
设ED=x,则EC=5﹣x,FC=BC﹣BG=13﹣12=1,
在Rt△EFC中,由勾股定理得,
EC2+FC2=EF2,
即(5﹣x)2+12=x2,
解得x,
即DE,
∴S△ADEAD DE
13
,
答:△ADE的面积为.
23.【解答】解:(1)由式子的变化规律得:,
故答案是:;
(2)sn=a1+a2+a3+ +an
,
当n=4时,;
(3)∵
.
24.【解答】解:(1)AE⊥BF,理由如下:
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°,
在Rt△ABE和Rt△BCF中,
,
∴Rt△ABE≌Rt△BCF(HL),
∴∠BAE=∠CBF,
∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴AE⊥BF;
(2)在Rt△ABE中,AB=8,BE=6,
根据勾股定理得:AE10,
∵S△ABEAB BEAE BP,
∴8×6=10BP,
∴BP=4.8,
∴BP的长度为4.8;
(3)四边形FMNP不能成为正方形,理由如下:
由(1)知:AE⊥BF,
∴∠APF=90°,
∵FM⊥DN,DN⊥AE,
∴∠FMN=∠MNP=90°,
∴四边形FMNP是矩形,
∵∠BAP+∠NAD=∠NAD+∠ADN=90°,
∴∠BAP=∠ADN,
在△BAP和△ADN中,
,
∴△BAP≌△ADN(ASA),
∴AN=BP,AP=DN,
∵AE=BF,
∴AE﹣AN=BF﹣BP,
∴EN=PF,
∵点F在线段CD上运动时(点F不与C、D重合),
∴P、E不重合,
∴PN≠PF,
∴四边形FMNP不能成为正方形.
25.【解答】解:(1)∵,
∴24﹣2c≥0,c﹣12≥0,
∴c=12,
∴a=c=12,
∴A(0,12),C(12,0);
(2)∵四边形OABC是矩形,A(0,12),C(12,0),
∴OC=OA=AB=BC=12,AB∥OC,
∵,
∴OE18,
∴AE=6,
如图,若AB与CE交点G,取BG的中点K,CG的中点H,连接KH,则GK=KB,
∴KH是△BCG的中位线,
∴,KH∥BC,
∴KH=AE=6,∠GKH=∠GAE,∠GHK=∠GEA,
∴△AGE≌△KGH(ASA),
∴GK=AG,
∴AG=GK=KB,
∵AB=12,
∴AG=GK=KB=4,
∵∠OCF的平分线交y轴于点E,
∴∠FCG=∠OCE,
∵AB∥OC,
∴∠BGC=∠OCE,
∴∠FCG=∠OCE=∠BGC,
∴CF=FG,
∴BF=FG﹣BG=CF﹣8,
∵BF2+BC2=CF2,
∴(CF﹣8)2+122=CF2,
解得CF=13;
(3)ON2、BM2、MN2之间的数量关系为BM2+ON2MN2,
证明:∵四边形OABC是矩形,A,C两点坐标分别为A(0,a),C(c,0),
∴OA=BC=a,OC=AB=c,
设AM=x,则BM=c﹣x,
∵∠AMN=45°,
∴AM=AN=x,,
∴ON=a﹣x,
过C向下作PC⊥CM,使PC=CM,过P作PD⊥x轴于D,过N作NQ⊥PD于点Q,
∴∠PDC=∠B=∠BCO=90°,∠PCD=∠BCM=90°﹣∠DCM,
∴△PCD≌△MCB(AAS),
∴CD=CB=a,PD=BM=c﹣x,BC=CD=a,
∴OD=a﹣c,
∵∠MCN=45°,
∴∠BCM+∠DCN=∠PCD+∠DCN=45°,
∴∠MCN=∠PCN=45°,
∵PC=CM,CN=CN,
∴△CMN≌△CPN(SAS),
∴,
∵PD⊥x轴,NQ⊥PD,∠NOD=90°,
∴∠ODQ=∠Q=∠NOD=90°,
∴四边形ONQD是矩形,
∴QD=ON=a﹣x,QN=OD=a﹣c,
∴PQ=PD+QD=a﹣x+c﹣x=a+c﹣2x,
∵PQ2+QN2=PN2,
∴,
∴a2+c2﹣2ax﹣2cx=﹣x2,
∵BM=c﹣x,,ON=a﹣x,
∴BM2+ON2=(c﹣x)2+(a﹣x)2=a2+c2﹣2ax﹣2cx+2x2=﹣x2+2x2=x2,MN2=2x2,
∴BM2+ON2MN2.
21世纪教育网(www.21cnjy.com)
同课章节目录
