3.2复数的四则运算 教学课件(共28张PPT)高中数学湘教版(2019)必修第二册
文档属性
| 名称 | 3.2复数的四则运算 教学课件(共28张PPT)高中数学湘教版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 36.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-06 12:48:04 | ||
图片预览







文档简介
(共28张PPT)
3.2复数的四则运算
湘教版(2019)必修第二册
第三章 复数
01
掌握复数的四则运算,并会简单运用,提高逻辑素养能力(重点)
02
了解复数四则运算的几何意义,提高逻辑素养能力(难点)
新课导入
上一节我们学习了复数的一些相关概念以及它的几何意义,我们知道运算是“数”的最主要的功能,复数不同于实数,它是由实部、虚部两部分构造而成的整体,它如何进行运算呢?
实部
虚部
我们这节课就来学习一下简单的复数运算——复数的加、减运算及其几何意义.
新课导入
建立了复数的概念以后,一个很重要的问题就是复数之间如何运算。
由于任意两个实数进行加、减、乘、除运算(做除法时除数不为0)仍得到实数,因此由实数集扩充得到的复数集里的各种运算应当和实数集里的运算是一致的.
新知探究
复数的加法法则
z1+ z2=(a+bi) + (c+di) = (a+c) + (b+d)i
实部相加为实部
虚部相加为虚部
两个复数的和仍然是一个确定的复数
特别地,当z1,z2都是实数时,把它们看作复数时的和就是这两个实数的和.
两个复数相加,类似于两个多项式相加
新知探究
复数的加法满足的运算律
新知探究
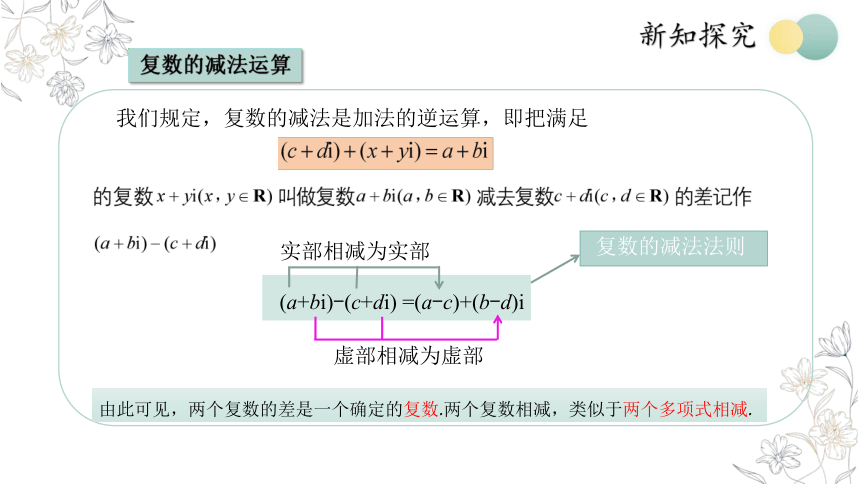
我们规定,复数的减法是加法的逆运算,即把满足
复数的减法运算
(a+bi)-(c+di) =(a-c)+(b-d)i
实部相减为实部
虚部相减为虚部
由此可见,两个复数的差是一个确定的复数.两个复数相减,类似于两个多项式相减.
复数的减法法则
新知探究
新知探究
在初中,我们学习过两个多项式相乘,例如(a+b)(c+d)=(a+b)(c+d)=ac+ad+bc+bd ,那么,在复数集上,复数z1=a+bi, z2=c+di,其中a,b,c,d∈R,z1·z2=(a+bi)(c+di)是如何计算的,计算方法和上述两个多项式相乘一样,如果不一样,那么有什么区别呢?
新知探究
复数的乘法法则
z1z2=(a+bi) (c+di )=
(ac-bd)
+(ad+bc)i
(a+bi)(c+di)=ac+bci+adi+bdi2
i2=-1
=(ac-bd)+(ad+bc)i
新知探究
复数的乘法法则的两点说明
1.两个复数的积是一个确定的复数. 特别地, 当z1,z2都是实数时, 把它们看作复数时的积就是这两个实数的积.
2.可以看出, 两个复数相乘, 类似于两个多项式相乘, 只要在所得的结果中把 i2 换成 -1 , 并且把实部与虚部分别合并即可.
新知探究
拓展:复数的乘法公式的拓展
新知探究
思考:复数的乘法是否满足交换律、结合律呢?乘法对加法满足分配律吗?
交换律: z1z2=z2z1
结合律:(z1z2)z3=z1(z2z3)
分配律: z1(z2+z3)= z1z2+z1z3
新知探究
复数的乘方
规定i0=1
新知探究
复数除法法则
1.两个复数相除 (除数不为 0 ), 所得的商是一个确定的复数.
课堂巩固
课堂巩固
课堂巩固
课堂巩固
课堂巩固
课堂巩固
课堂巩固
当堂检测
C
当堂检测
C
当堂检测
当堂检测
B
当堂检测
4
感谢聆听
Thank You
3.2复数的四则运算
湘教版(2019)必修第二册
第三章 复数
01
掌握复数的四则运算,并会简单运用,提高逻辑素养能力(重点)
02
了解复数四则运算的几何意义,提高逻辑素养能力(难点)
新课导入
上一节我们学习了复数的一些相关概念以及它的几何意义,我们知道运算是“数”的最主要的功能,复数不同于实数,它是由实部、虚部两部分构造而成的整体,它如何进行运算呢?
实部
虚部
我们这节课就来学习一下简单的复数运算——复数的加、减运算及其几何意义.
新课导入
建立了复数的概念以后,一个很重要的问题就是复数之间如何运算。
由于任意两个实数进行加、减、乘、除运算(做除法时除数不为0)仍得到实数,因此由实数集扩充得到的复数集里的各种运算应当和实数集里的运算是一致的.
新知探究
复数的加法法则
z1+ z2=(a+bi) + (c+di) = (a+c) + (b+d)i
实部相加为实部
虚部相加为虚部
两个复数的和仍然是一个确定的复数
特别地,当z1,z2都是实数时,把它们看作复数时的和就是这两个实数的和.
两个复数相加,类似于两个多项式相加
新知探究
复数的加法满足的运算律
新知探究
我们规定,复数的减法是加法的逆运算,即把满足
复数的减法运算
(a+bi)-(c+di) =(a-c)+(b-d)i
实部相减为实部
虚部相减为虚部
由此可见,两个复数的差是一个确定的复数.两个复数相减,类似于两个多项式相减.
复数的减法法则
新知探究
新知探究
在初中,我们学习过两个多项式相乘,例如(a+b)(c+d)=(a+b)(c+d)=ac+ad+bc+bd ,那么,在复数集上,复数z1=a+bi, z2=c+di,其中a,b,c,d∈R,z1·z2=(a+bi)(c+di)是如何计算的,计算方法和上述两个多项式相乘一样,如果不一样,那么有什么区别呢?
新知探究
复数的乘法法则
z1z2=(a+bi) (c+di )=
(ac-bd)
+(ad+bc)i
(a+bi)(c+di)=ac+bci+adi+bdi2
i2=-1
=(ac-bd)+(ad+bc)i
新知探究
复数的乘法法则的两点说明
1.两个复数的积是一个确定的复数. 特别地, 当z1,z2都是实数时, 把它们看作复数时的积就是这两个实数的积.
2.可以看出, 两个复数相乘, 类似于两个多项式相乘, 只要在所得的结果中把 i2 换成 -1 , 并且把实部与虚部分别合并即可.
新知探究
拓展:复数的乘法公式的拓展
新知探究
思考:复数的乘法是否满足交换律、结合律呢?乘法对加法满足分配律吗?
交换律: z1z2=z2z1
结合律:(z1z2)z3=z1(z2z3)
分配律: z1(z2+z3)= z1z2+z1z3
新知探究
复数的乘方
规定i0=1
新知探究
复数除法法则
1.两个复数相除 (除数不为 0 ), 所得的商是一个确定的复数.
课堂巩固
课堂巩固
课堂巩固
课堂巩固
课堂巩固
课堂巩固
课堂巩固
当堂检测
C
当堂检测
C
当堂检测
当堂检测
B
当堂检测
4
感谢聆听
Thank You
同课章节目录
